электротехника. 31. Расчет электрических цепей операционным методом
 Скачать 145.5 Kb.
|
|
§31. Расчет электрических цепей операционным методом Методы операционного исчисления широко применяются, в частности, для расчета электрических цепей. Пусть i(t) и u(t) – ток и напряжение в электрической цепи. Применение операционных методов основано на справедливости законов Кирхгофа для операторных тока  и напряжения  . В самом деле, законы Кирхгофа – линейные соотношения, связывающие действительные функции (оригиналы). В силу линейности преобразования Лапласа, те же соотношения будут связывать и образы исходных функций.Запишем законы Ома для основных элементов электрической цепи: Падение напряжения на сопротивлении R  ,на индуктивности L  ,на емкости C 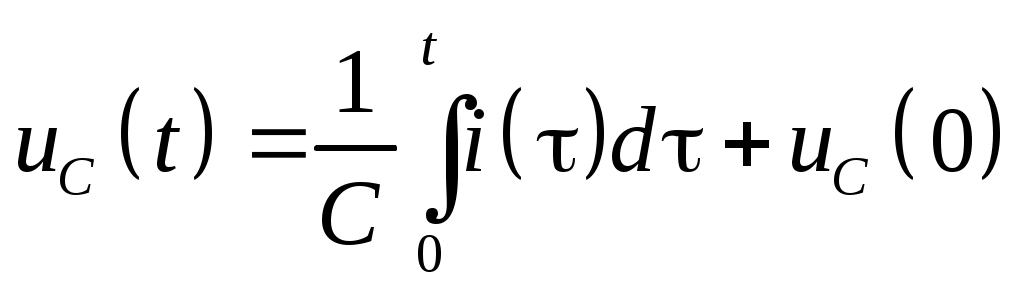 .Получим изображения по Лапласу этих соотношений  , , .Т.о. закон Ома в операторной форме для произвольного участка цепи  ,где Z(p) – операторное сопротивление участка цепи, которое для участков с сопротивлением R, индуктивностью L и емкостью C имеют вид соответственно  ,  ,  .При ненулевых начальных условиях к источникам ЭДС, имеющимся в цепи следует добавить дополнительно Li(0) и –uC(0)/p – запасы энергии в индуктивности и емкости. Примеры. Найти ток в цепи с последовательно включенными L, R, C при подключении постоянной ЭДС e(t)=E, если uC(0)=u0. 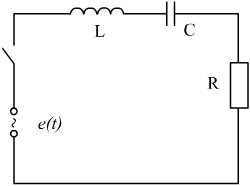 Образ постоянной ЭДС  , дополнительная ЭДС из начальных условий –u0/p, полное операторное сопротивление  .Т.о.   Оригинал в данном случае легко угадывается, действительно 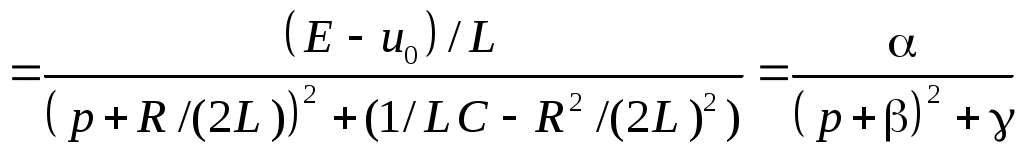  ,где 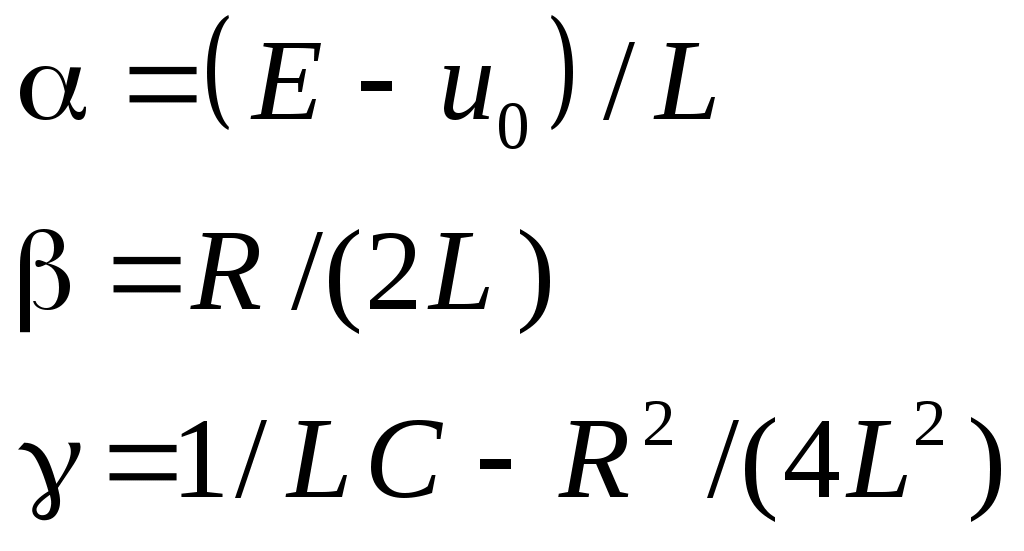 .В зависимости от значения может быть три разных случая. 1) 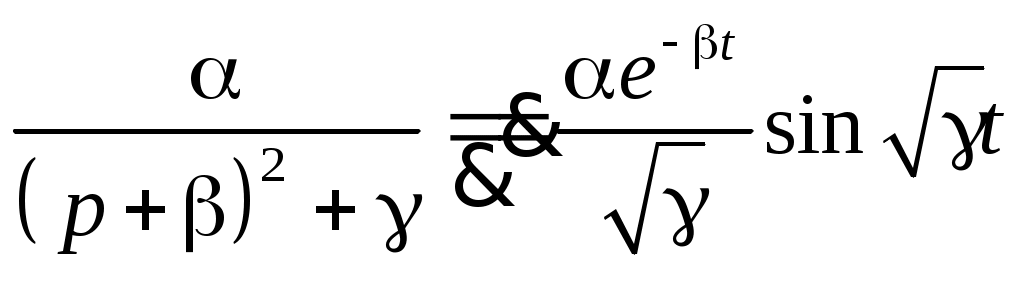 , тогда  2) 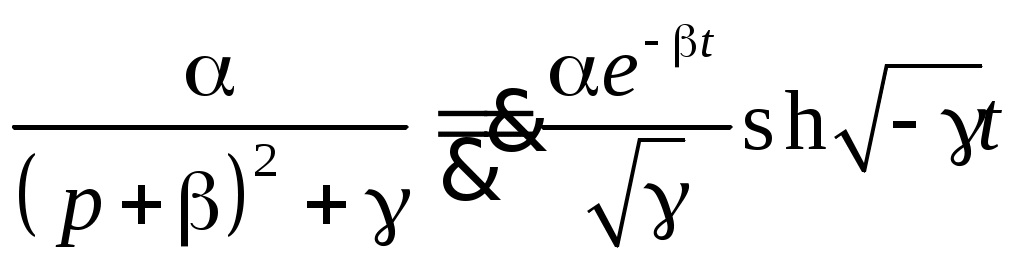 , тогда  3)  , тогда  Вспоминая реальные обозначения, получим ток в данной цепи 1) 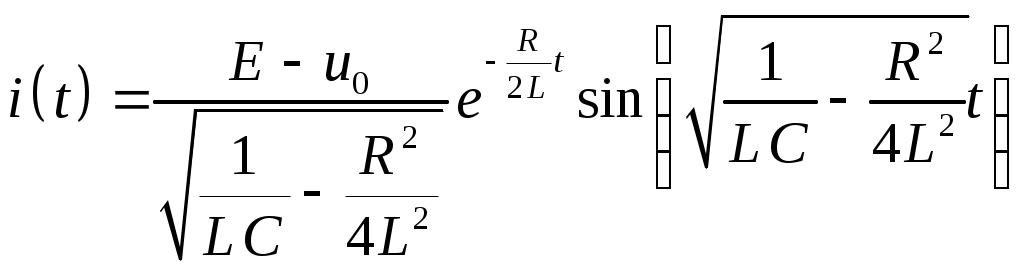 , тогда  2) 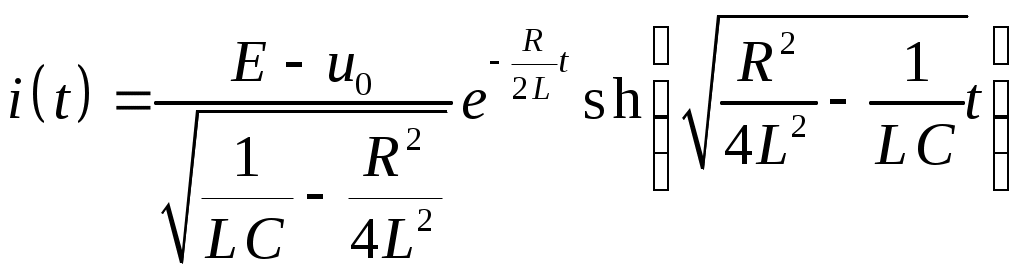 , тогда  3)  , тогда  .Найти напряжение на индуктивности L1 при подключении постоянной ЭДС e(t)=E и нулевых начальных условиях. (последовательно к индуктивности подключены параллельно R и L2) 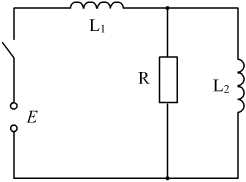 Образ постоянной ЭДС , дополнительных ЭДС из начальных условий в этой задаче нет. Запишем законы Кирхгофа   Выразим соответствующие операторные напряжения по закону Ома   Собирая все в одно уравнение, получим образ Лапласа искомого напряжения 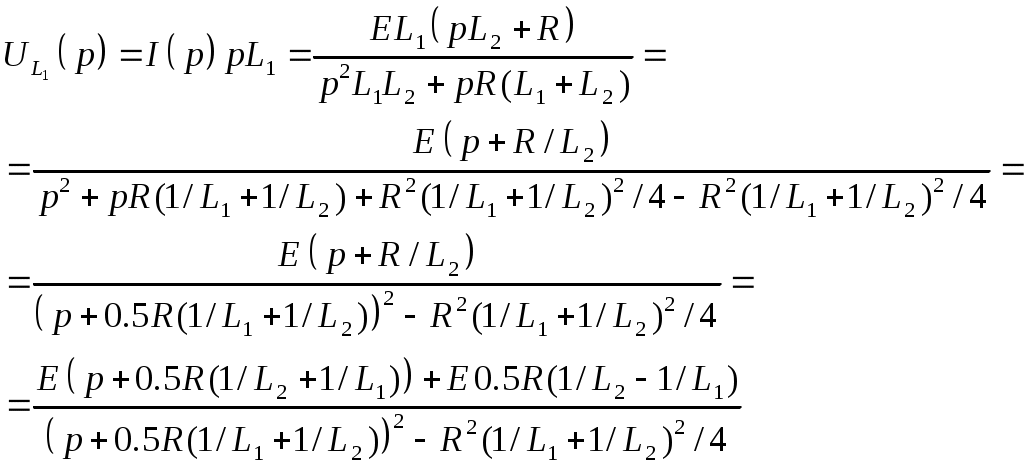 Искомое напряжение 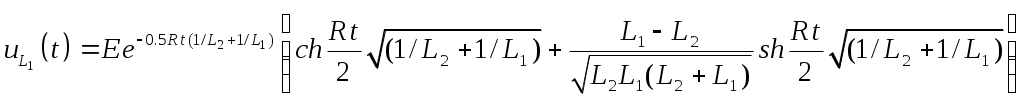 Если ЭДС зависит от времени? Если воздействие на схему зависит от времени, то полезно использовать интеграл Дюамеля. Для этого сначала определяется переходная характеристика цепи – закон изменения напряжения или тока при подаче на вход единичного напряжения e(t)=(t). Операторный ток при этом  где Z(p) – операторное сопротивление цепи. Если теперь на ту же схему подается произвольное напряжение 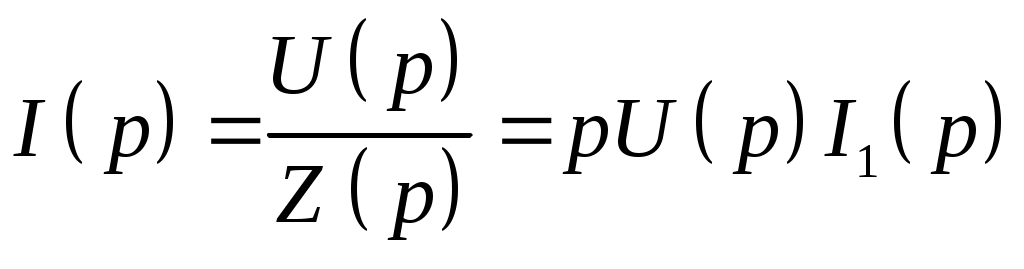 , то  .И тогда ток в цепи вычисляется при помощи интеграла Дюамеля  .Пример. Найти ток в RL-цепи при подключении ЭДС 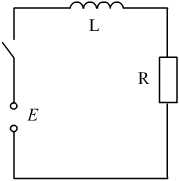 . Определим переходную характеристику цепи.   Ток при зависящем от времени ЭДС вычисляем при помощи интеграла Дюамеля 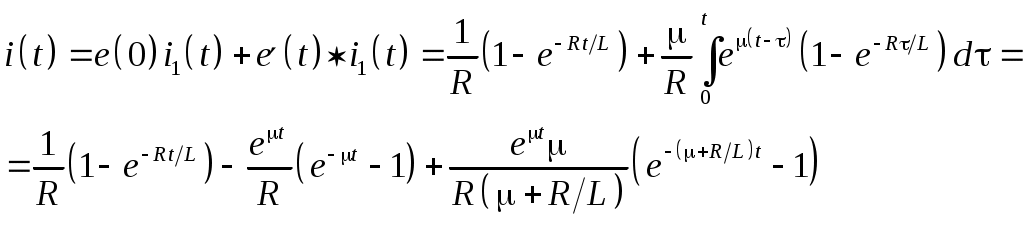 |