Метод наложения. Лабораторная работа 2 Расчет электрических цепей методом наложени я
 Скачать 73.17 Kb. Скачать 73.17 Kb.
|
|
Лабораторная работа № 2 Расчет электрических цепей методом наложения Цель работы: Отработка практических навыков проведения эксперимента и расчета электрических цепей методом наложения. Краткая теория Метод наложения применяют для расчета сложных электрических цепей, имеющих несколько источников питания. Он основан на принципе наложения (суперпозиции): ток в какой-либо ветви сложной цепи равен алгебраической сумме токов, вызываемых в этой ветви каждым источником в отдельности. Чтобы определить токи методом наложения, нужно: а) В исследуемой электрической цепи удалить все источники питания, оставив их внутренние сопротивления, кроме одного, (идеальные источники ЭДС закоротить, а идеальные источники тока разомкнуть) и определить все токи от воздействия этого источника питания. (Схему с одним источником называют расчетной, а токи в ней – частичными) б) Определить частичные токи от действия каждого источника ЭДС в отдельности. в) Найти результирующий ток в каждой ветви исследуемой схемы как алгебраическую сумму частичных токов, создаваемых от всех источников питания. Например, зная частичные токи в расчетных схемах ( рисунок 1 в, с), определим токи  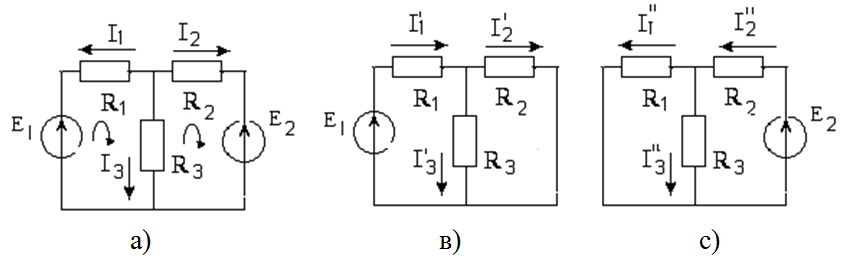 Рисунок 1- а) - исследуемая схема в), с) - расчетные схемы Уравнение баланса мощностей. В электротехнике существует понятие мощности источника и мощности потребителя. Мощность источника – это скорость, с которой неэлектрическая энергия в источнике преобразуется в электрическую 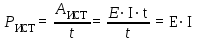 Мощность приемника – это скорость, с которой в приемнике электрическая энергия преобразуется в неэлектрическую 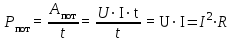 В любой электрической цепи должен соблюдаться энергетический баланс – алгебраическая сумма мощностей всех источников должна быть равна арифметической сумме мощностей всех приемников энергии: ∑ EI =∑I2R Это равенство называют балансом мощности электрической цепи. Если направление ЭДС источника совпадает с направлением тока, то он работает в режиме генератора, т. е. поставляет электрическую энергию в цепь. Его ЭДС имеет знак плюс. Если направление ЭДС противоположно направлению тока, то он работает в режиме потребителя, т. е. потребляет электрическую энергию. Его ЭДС имеет знак минус. В уравнении баланса мощности нужно учитывать знак ЭДС источника. Порядок выполнения работы 1)Собрать исследуемую схему (рисунок 2). В качестве источников Е1и Е2 взять нерегулируемый и регулируемый источники напряжения постоянного тока (Е1=15 В; Е2=5 ÷ 15 В). 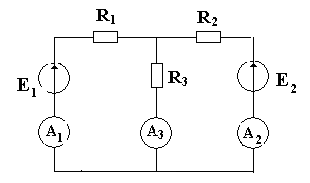 Рисунок 2 2) Измерить токи и напряжения в исследуемой схеме. Результаты измерений занести в таблицу 1. Таблица 1
3)Перейти к первой расчетной схеме с источником ЭДС Е1(Е2=0) (рисунок3)  Рисунок 3 Измерить в первой расчетной схеме ЭДС Е1, все частичные токи и напряжения, указав их направления на схеме. Результаты измерений занести в таблицу 2. Таблица 2
4)Перейти ко второй расчетной схеме с источником ЭДС Е2 (Е1=0) (рисунок 4). 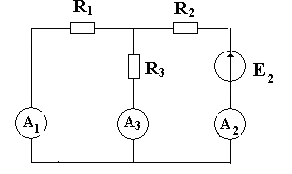 Рисунок 4 • Измерить во второй расчетной схеме ЭДС Е2, все частичные токи и напряжения, указав их направления на схеме. Результаты измерений занести в таблицу 3. Таблица 3
• Зная частичные токи и напряжения в двух расчетных схемах, рассчитать токи и напряжения в исследуемой схеме с двумя источниками питания как алгебраическую сумму частичных токов и напряжений и указать их направления на рисунке 2. Результаты расчетов занести в таблицу 1 и сравнить их с измеренными значениями. • Составить уравнения баланса мощностей в исследуемой и расчетных схемах. Ответить на вопрос: «Можно ли пользоваться методом наложения для вычисления мощностей?» • Сделать выводы по работе. Контрольные вопросы и задачи 1 На каком принципе основан метод наложения и в чем заключается сущность этого метода? 2 Для схемы (рисунок 5) докажите справедливость формул для тока I1иI2. 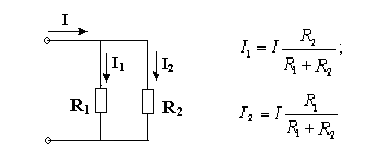 Рисунок 5 3 Рассчитайте частичные токи в первой и второй расчетных схемах, изображенных на рисунках 3 и 4. Сравните их с измеренными токами. 4 Для схемы (рисунок 6) методом наложения найдите токи в ветвях, если R1 = 2 Oм; R2 = 6 Oм; R3 = 4 Oм; J = 5 A; E = 20 B. 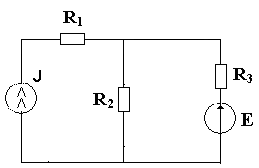 Рисунок 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
