КОНТРОЛЬНЫЕ ВОПРОСЫ
Что понимают под биореологией? Каковы особенности строения и физические свойства костной ткани? Какие виды деформации являются наиболее опасными для костной ткани? Каково влияние видов деформации на генез костей?
Какими механическими свойствами обладают мышцы? Как изменяется содержание компонентов сосудистой ткани по ходу кровеносной системы? Какие основные модели сокращения мышц Вы знаете? Что понимают под абсолютной мышечной силой?
Каково строение и механические свойства кровеносных сосудов? Что понимают под криволинейной ортотропией кровеносных сосудов?
Каково строение и механические свойства легких? Что понимают под гистерезисом легких?
III. Некоторые вопросы реологии жидкости и ее приложение к крови. Физические основы гемодинамики.
Жидкие среды составляют наибольшую часть организма. Их движение, в частности крови, обеспечивает нормальную жизнедеятельность организма. Механические свойства крови зависят от ее состава, характеристик и особенностей составляющих компонентов крови, плотности крови, ее вязкости и т.д. Малые изменения многих отдельных компонентов крови или параметров могут привести к существенному изменению ее механических свойств.
Вопросами движения крови и ее взаимодействие при этом со стенками сосудов занимается гемодинамика.
3.1 Вязкость жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости.
Вязкость жидкости (или внутреннее трение) – это динамическое свойство жидкости, обусловленное силами межмолекулярного взаимодействия. Вязкость жидкости проявляется либо при движении самой жидкости, либо при движении тела в покоящейся жидкости. Мы будем рассматривать только движение самой жидкости.
Рис. 3.1
П 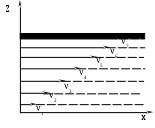 усть вязкая жидкость движется между двумя твердыми пластинками, из которых нижняя пластинка неподвижна, а верхняя движется со скоростью 7. Движение жидкости можно представить в виде параллельных слоев, движущихся с определенными скоростями. Причем, слой, непосредственно соприкасающийся с нижней пластинкой за счет явления «прилипания», будет неподвижен. Скорости последующих слоев будут увеличиваться и максимальная скорость будет у слоя, непосредственно соприкасающегося с движущейся пластинкой. На рис.3.1 схематично представлено распределение скорости слоев при движении вязкой жидкости, при этом 1234567. усть вязкая жидкость движется между двумя твердыми пластинками, из которых нижняя пластинка неподвижна, а верхняя движется со скоростью 7. Движение жидкости можно представить в виде параллельных слоев, движущихся с определенными скоростями. Причем, слой, непосредственно соприкасающийся с нижней пластинкой за счет явления «прилипания», будет неподвижен. Скорости последующих слоев будут увеличиваться и максимальная скорость будет у слоя, непосредственно соприкасающегося с движущейся пластинкой. На рис.3.1 схематично представлено распределение скорости слоев при движении вязкой жидкости, при этом 1234567.
Ньютон установил, что между двумя слоями жидкости возникает сила внутреннего трения Fтр которая зависит от природы жидкости, прямо пропорциональна площади соприкасающихся слоев S и градиенту скорости 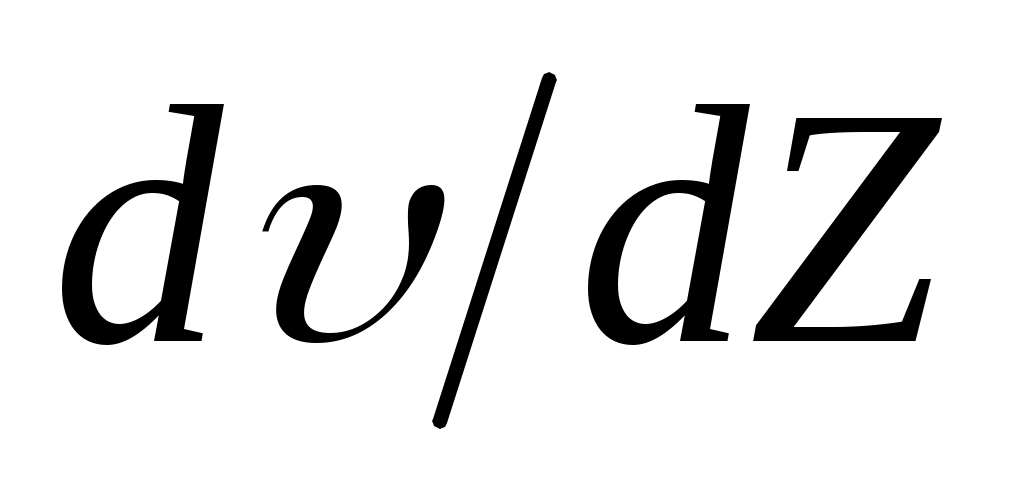 между ними: между ними:
Fтр=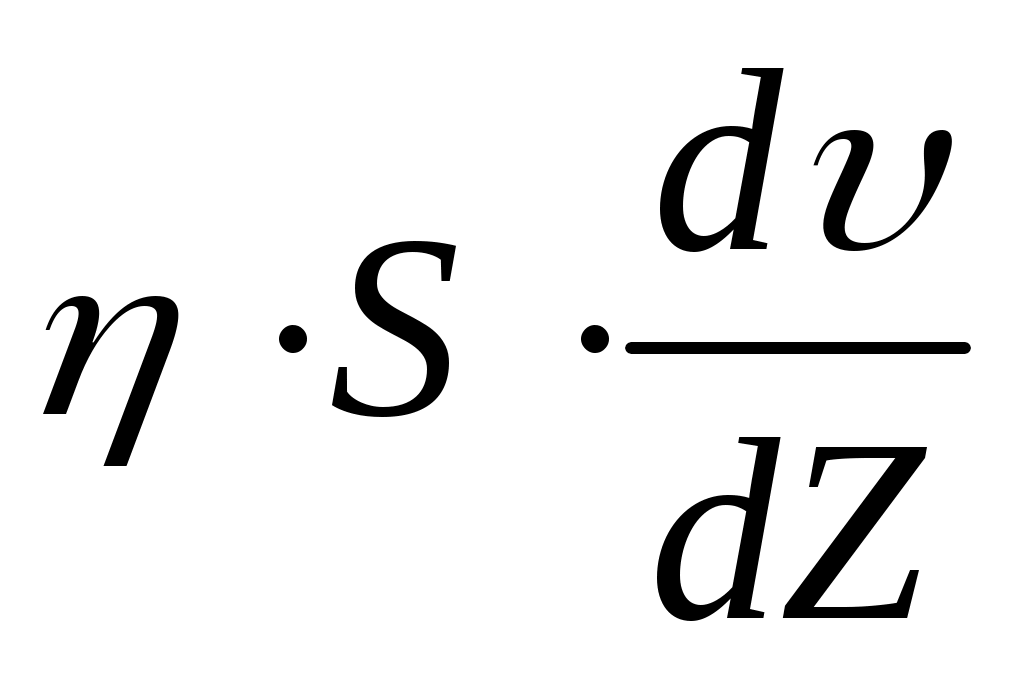 - уравнение Ньютона. (3.1) - уравнение Ньютона. (3.1)
где - коэффициент вязкости (или просто вязкость жидкости).
Сила внутреннего трения Fтр действует касательно к поверхности соприкасающихся слоев жидкости и направлена так, что ускоряет более медленно движущийся слой и замедляет более быстро движущийся слой. действует касательно к поверхности соприкасающихся слоев жидкости и направлена так, что ускоряет более медленно движущийся слой и замедляет более быстро движущийся слой.
Градиент скорости 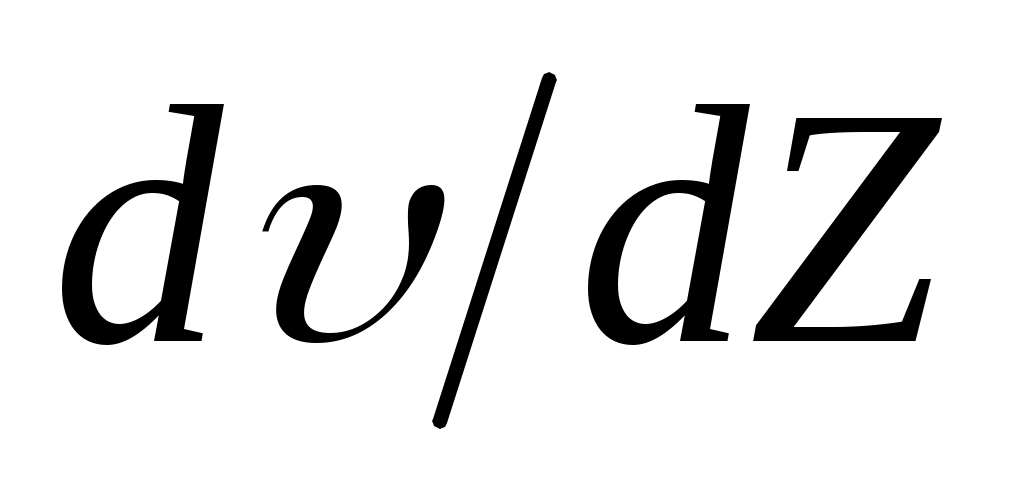 (скорость сдвига) характеризует быстроту изменения скорости при переходе от слоя к слою. Единицей измерения градиента скорости является с-1. (скорость сдвига) характеризует быстроту изменения скорости при переходе от слоя к слою. Единицей измерения градиента скорости является с-1.
Из уравнения Ньютона можно получить коэффициент вязкости:
=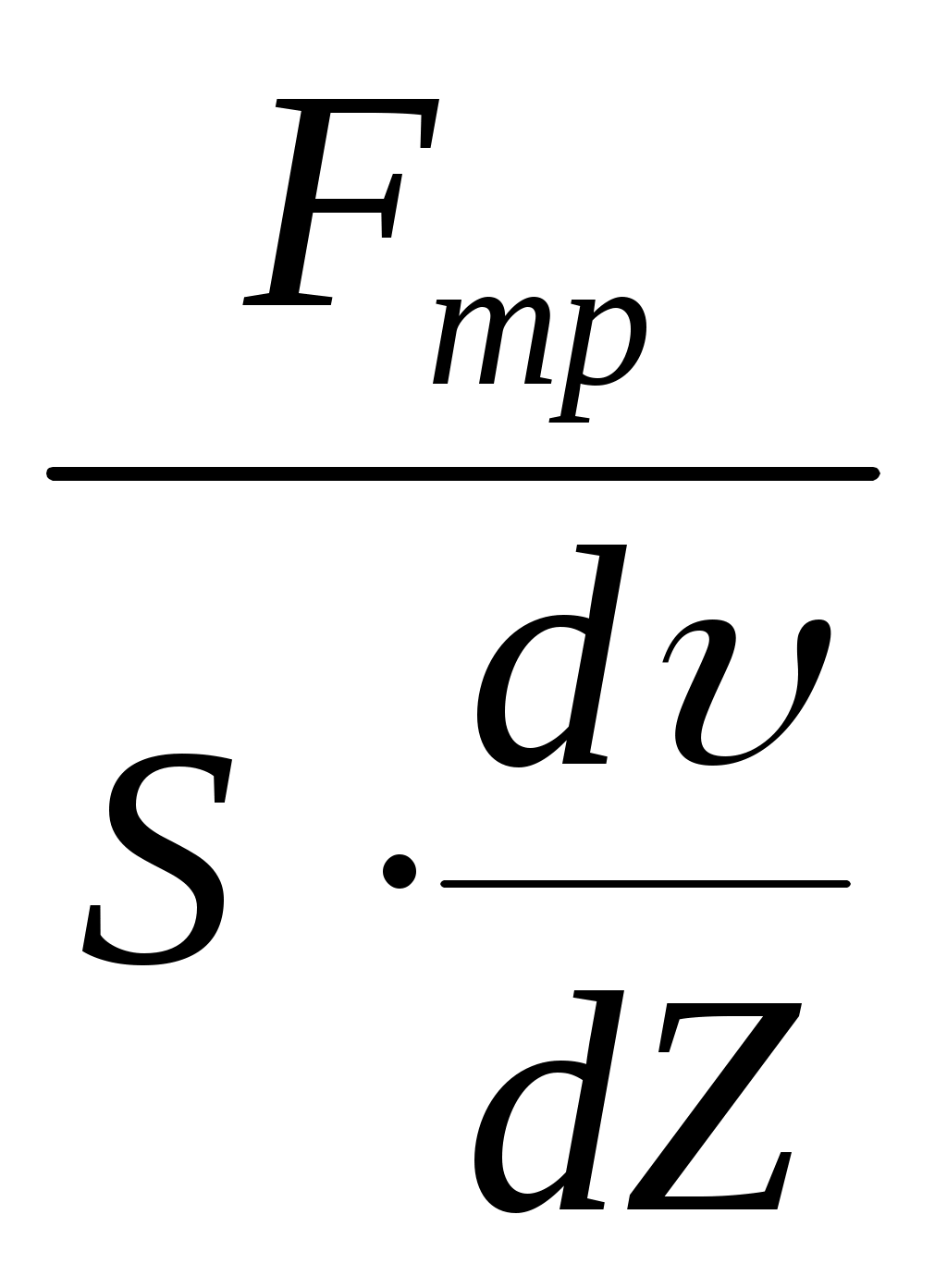 (3.2) (3.2)
Физический смысл коэффициента вязкости заключается в том, что он численно равен силе внутреннего трения Fтр, возникающей при течении между двумя слоями жидкости, соприкасающимися на площади, равной единице, при градиенте скорости между ними, равном единице. Единицей измерения коэффициента вязкости является Па с.
Внесистемной единицей измерения вязкости является Пуаз (П), причем 1Па∙с=10П.
На практике пользуются также понятием относительной вязкости отн которая равна:
отн=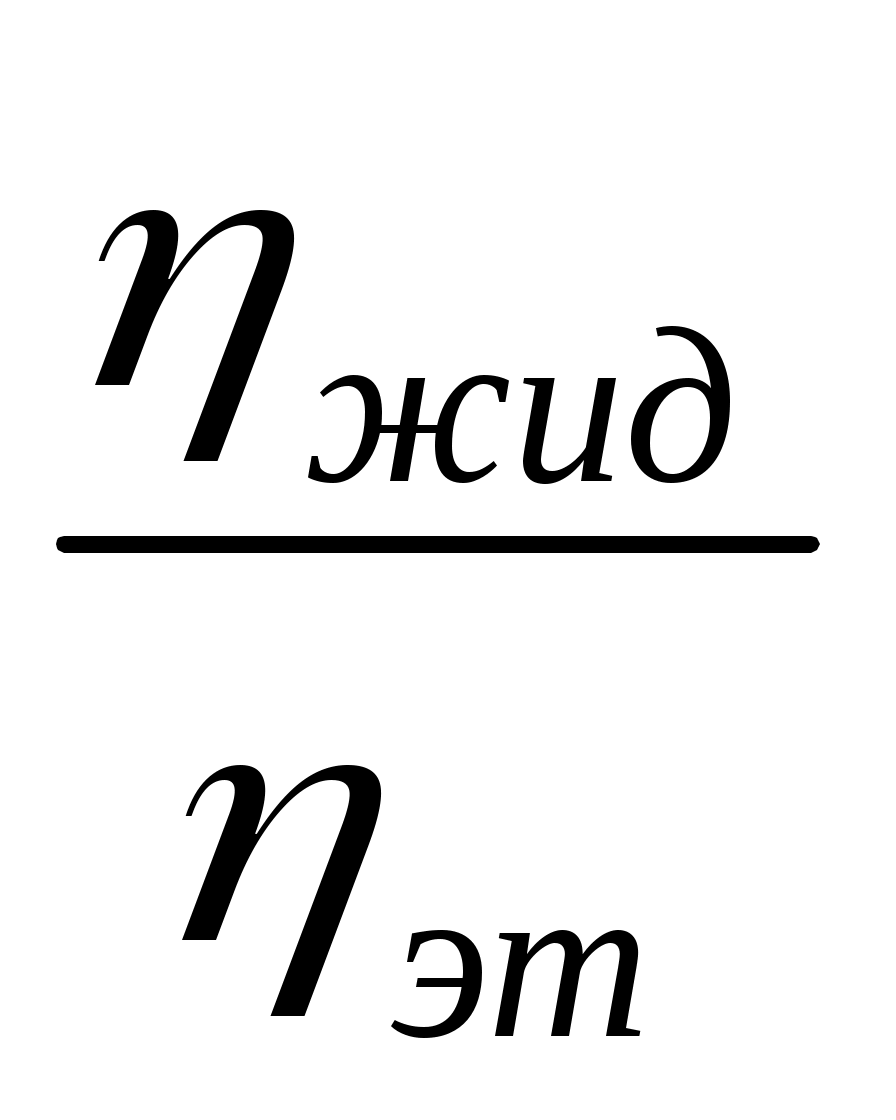 , (3.3) , (3.3)
где жид – вязкость данной жидкости, эт – вязкость эталонной жидкости. Относительная вязкость – величина безразмерная. В качестве эталона жидкости чаще всего выбирают воду т.к. вязкость воды при комнатной температуре равна 1сП.
Жидкости, коэффициент вязкости которых зависит от температуры и ее природы, называются ньютоновскими. К ним относят вода, низкомолекулярные органические соединения, расплавленные металлы и их соли.
Жидкости, вязкость которых зависит не только от температуры и природы, но и от давления и градиента скорости называются неньютоновскими. К ним относятся преимущественно растворы высокомолекулярных соединений (коллоидные, полимерные растворы, эмульсии, суспензии). Для неньютоновских жидкостей характерно то, что они состоят из сложных и крупных молекул. На реологические свойства таких жидкостей влияют собственные свойства структурных элементов: деформируемость (в частности, способность к упругой деформации), прочность, способность объединяться в агрегаты. Также важны особенности движения структурных элементов (вращение и ориентация в потоке, возможность их флуктуационного движения). Вязкость неньютоновских жидкостей при прочих равных условиях много больше, чем у ньютоновских жидкостей. Для неньютоновских жидкостей уравнение Ньютона не соблюдается. Вязкость неньютоновских жидкостей характеризуется условным коэффициентом вязкости, который относится к определенным условиям течения жидкости (давление, скорость).
3.2 Реологические свойства крови.
Кровь по своей природе является неньютоновской жидкостью, т.к. она представляет собой суспензию форменных элементов в белковом растворе плазмы. Реологическое поведение крови определяют концентрация и механические свойства только эритроцитов т.к. их содержание в крови составляет более 90%, а суммарный объем в 50 раз превышает объем лейкоцитов и тромбоцитов.
При течении крови по сосудам эритроциты концентрируются в центральной части потока крови, где вязкость соответственно увеличивается. Но поскольку вязкость крови невелика, этими явлениями пренебрегают, и коэффициент вязкости считают постоянной величиной. В норме относительная вязкость крови составляет: для мужчин 4.3 5.3 и для женщин 3.9 4.9.
Главным фактором, определяющим вязкость крови, является объемная концентрация эритроцитов, которая определяется по показателю гематокри:
Н=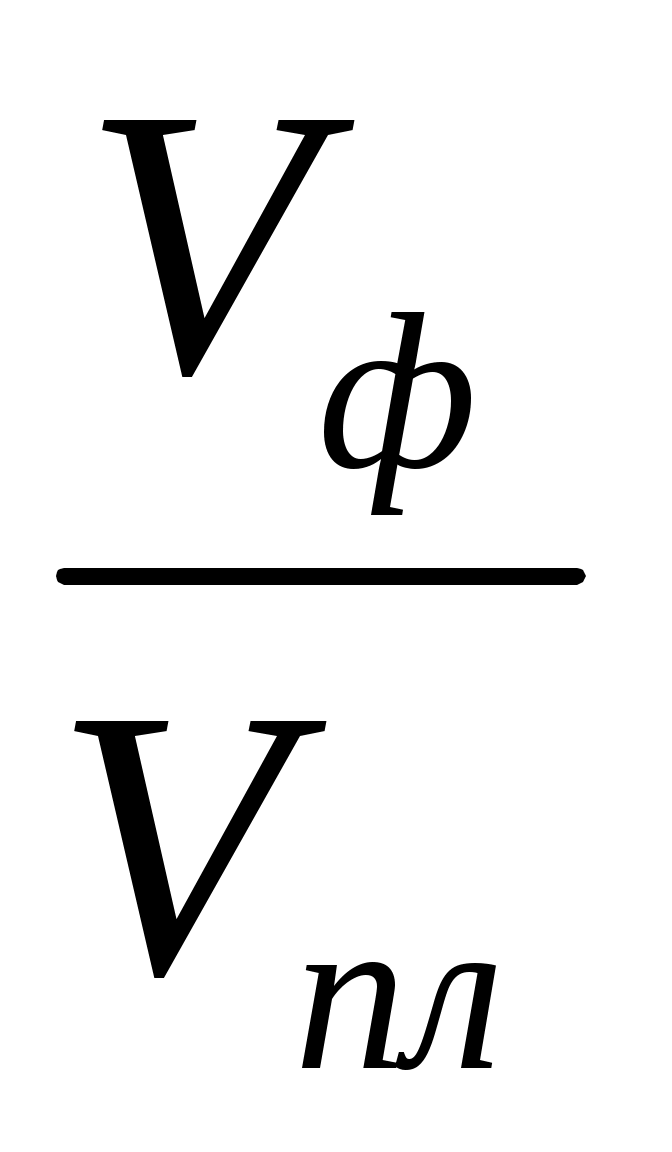 , (3.4) , (3.4)
где Vф - объем форменных элементов, Vпл – объем плазмы крови. В норме показатель гематокрита составляет 40% (или просто 0.4).
Кроме того, эритроциты в крови имеют способность агрегировать т.е. слипаться, образуя так называемые “монетные столбики” при небольших скоростях течения крови. Поэтому необходимо приложить некоторое напряжение сдвига с, чтобы кровь сдвинуть с места; при этом «монетные столбики» разрушаются: чем больше скорость крови, тем больше одиночных эритроцитов. Движущаяся кровь содержит как одиночные эритроциты, так и агрегаты. Это наблюдается при любых показателях гематокрита Н. В связи с этим, для определения вязкости крови используют, в отличие от ньютоновской жидкости, эмпирическое уравнение Кессона:
К= 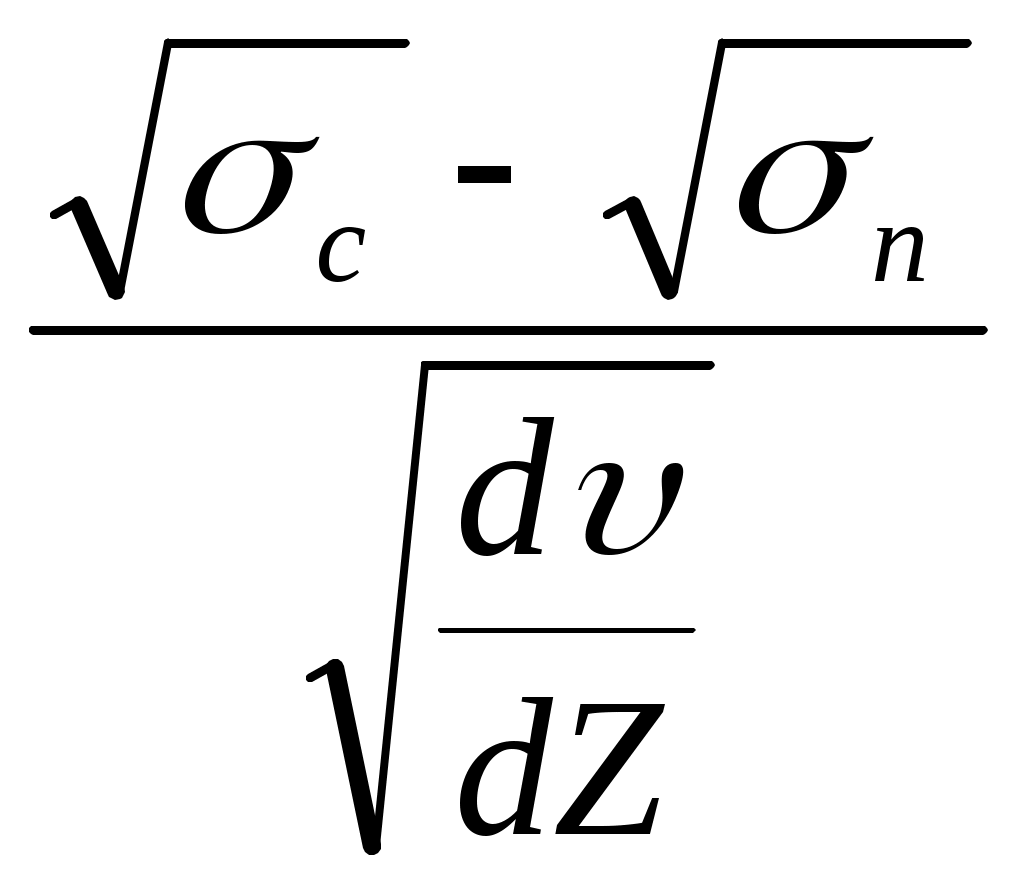 (3.5) (3.5)
где п - сonst (предел текучести крови), с – напряжение сдвига: кровь приходит в движение лишь при сп. Уравнение Кессона справедливо при скорости сдвига 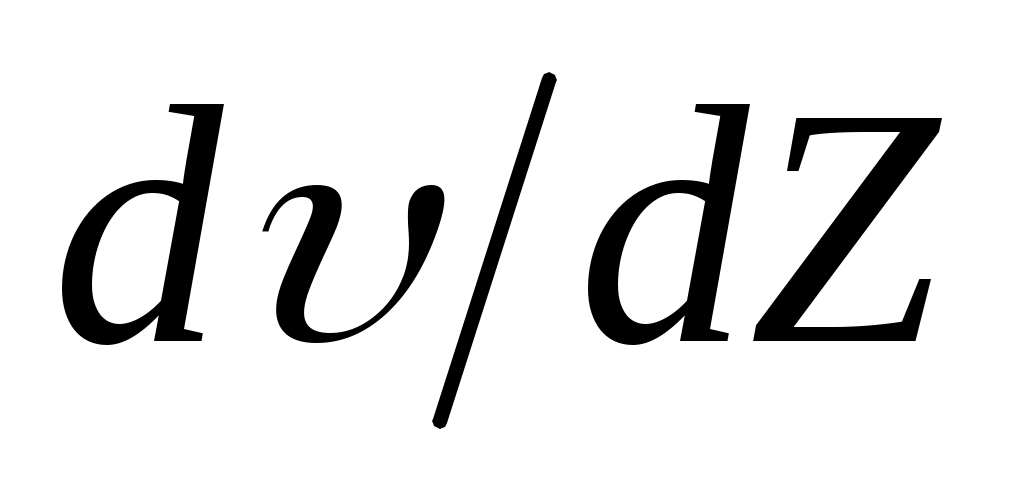 100 с-1. 100 с-1.
П
Рис.3.2
ри условии сп уравнение Кессона превращается в уравнение Ньютона, где =К2. График зависимости коэффициента вязкости от градиента скорости 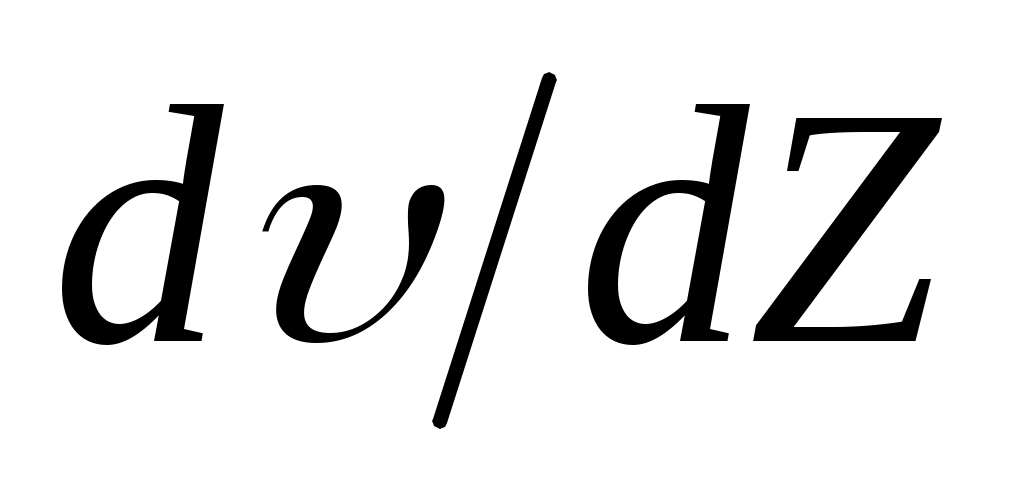 представлен на рис.3.2. Как видно из графика, при увеличении градиента скорости вязкость крови уменьшается до некоторого постоянного значения. Это связано с тем, что увеличение градиента скорости приводит к разрушению «монетных столбиков» и, соответственно, уменьшению вязкости крови до значения равного вязкости крови человека в норме. представлен на рис.3.2. Как видно из графика, при увеличении градиента скорости вязкость крови уменьшается до некоторого постоянного значения. Это связано с тем, что увеличение градиента скорости приводит к разрушению «монетных столбиков» и, соответственно, уменьшению вязкости крови до значения равного вязкости крови человека в норме.
На реологические свойства крови оказывает также влияние содержание белков в плазме: альбумина, глобулина, фибриногена. Из них, наименьшая вязкость у альбумина, наибольшая у фибриногена; так вязкость плазмы крови за счет содержания в ней фибриногена на 20% выше, чем вязкость сыворотки крови.
Относительная вязкость плазмы крови в норме: пл=1.51.8, сыворотки крови сыв=1.41.7. И плазма, и сыворотка крови являются ньютоновскими жидкостями. Несмотря на то, что по своей природе кровь является неньютоновской жидкостью, тем ни менее в первом приближении ее относят к ньютоновским жидкостям за счет небольшого коэффициента вязкости. При патологии относительная вязкость крови изменяется в пределах от 1.7 до 22.9.
3.3 Стационарное течение вязкой жидкости по горизонтальной трубе.
Течение жидкости называется стационарным, если в каждой точке данного объема, скорость ее частиц не изменяется. Движение жидкости изображают с помощью линий тока – это линии, касательные к которым совпадают с направлением скорости частиц. При стационарном течении жидкости, ее частицы движутся вдоль линий тока, сохраняя свое положение в пространстве неизменным. Часть потока жидкости, ограниченная линиями тока, называется трубкой тока. При течении жидкости по трубе, трубкой тока являются стенки трубы. Объем жидкости V, протекающий в единицу времени через любое перпендикулярное сечение S трубки, называется объемной скоростью движения жидкости и обозначается Q:
Q=V/ t. (3.6)
Учитывая, что V=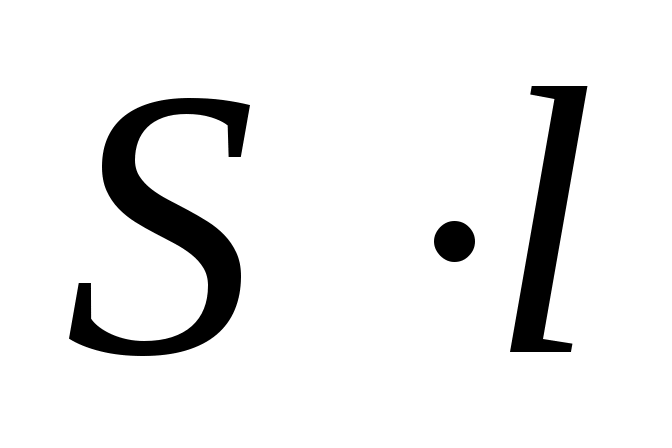 , а , а 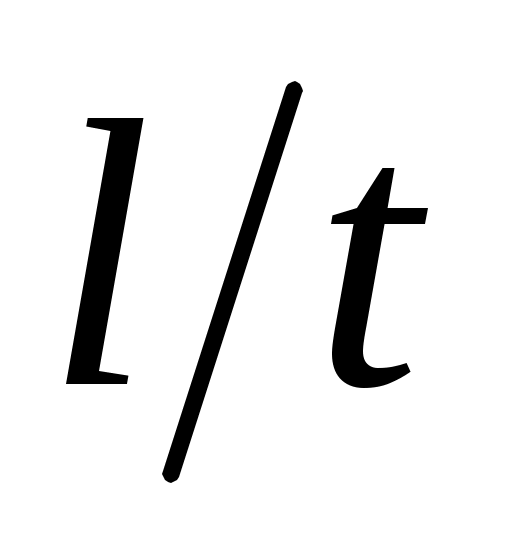 =ср, выражение (3.11) можно переписать: =ср, выражение (3.11) можно переписать:
Q =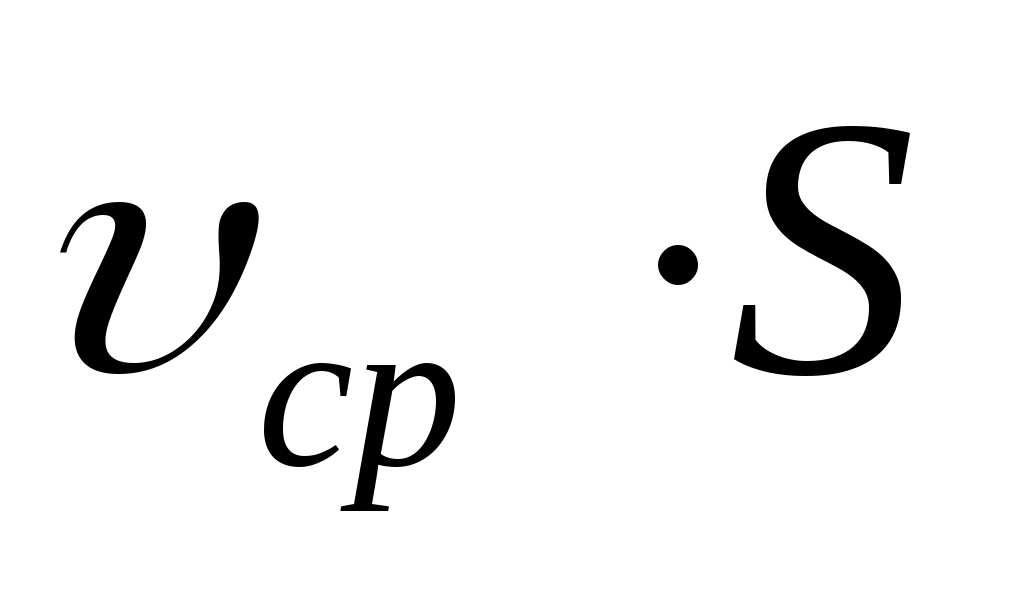 (3.7) (3.7)
Величина Q измеряется в м3с.
Для стационарного течения объемная скорость движения жидкости остается величиной постоянной, т.е. Q =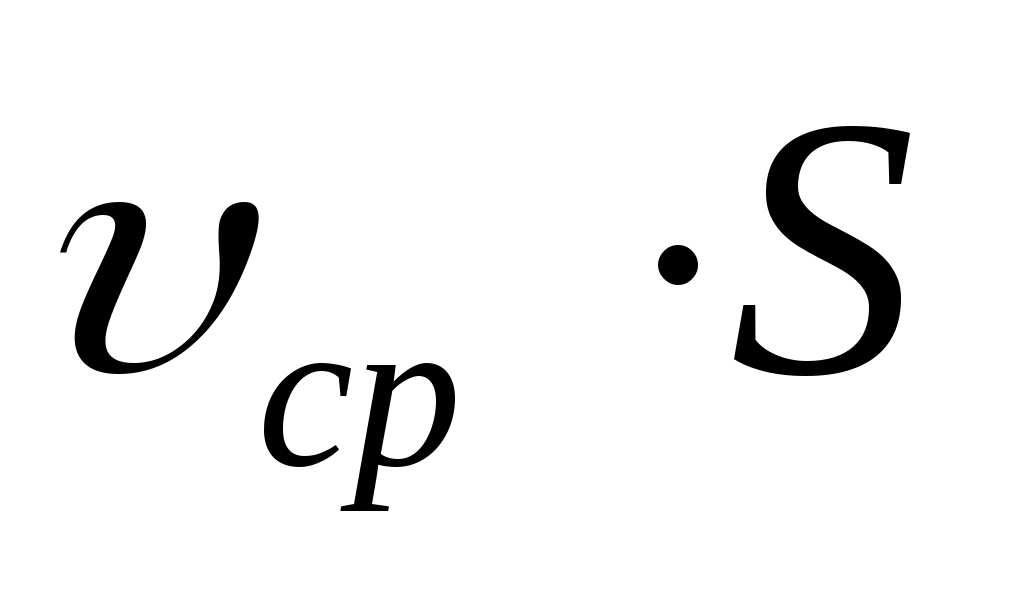 const (3.8) const (3.8)
Выражение (3.8) представляет условие стационарного течения жидкости, из которого следует, что чем уже труба, тем больше скорость движения жидкости и, наоборот.
3.4 Ламинарное и турбулентное течение жидкости. Число Рейнольдса.
Рассмотрим течение при относительно невысокой скорости вязкой жидкости по горизонтальной трубе с гладкими стенками постоянного сечения (рис.3.2).
Т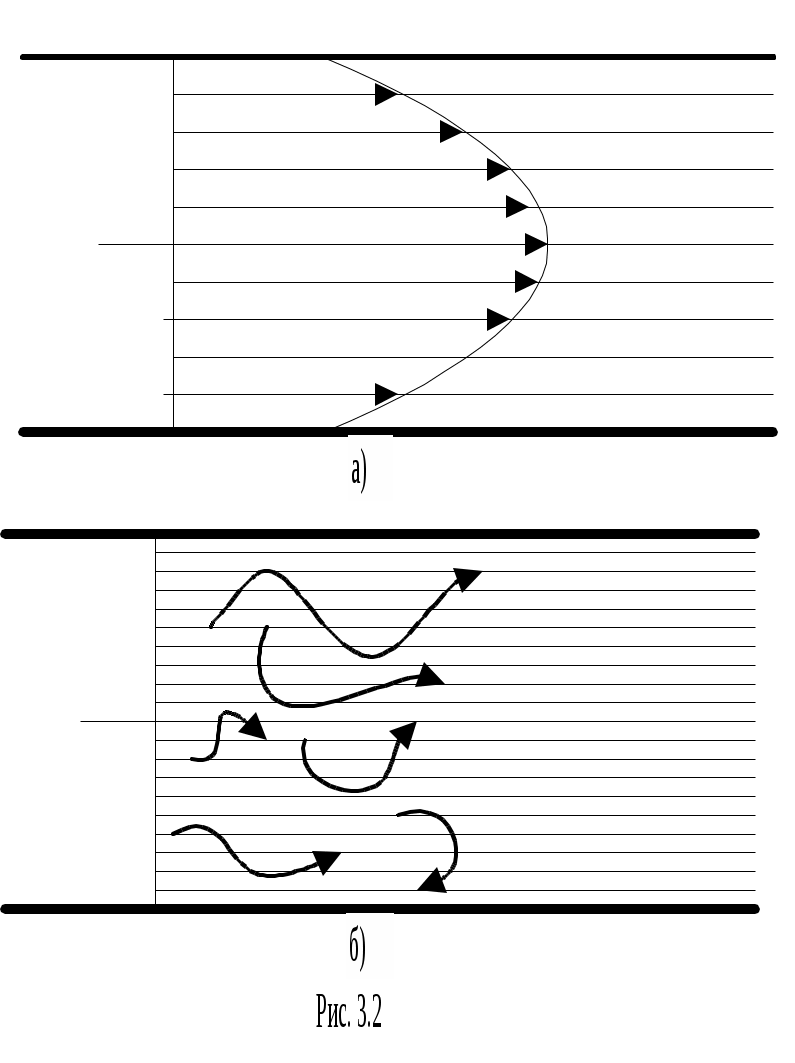 акое течение можно условно разделить на слои: слой молекул, прилегающий к стенке трубы, прилипает к ней, и остается практически неподвижен. Каждый последующий слой молекул, смещаясь относительно предыдущего слоя, двигается по отношению к стенке трубы с постепенно возрастающей скоростью. Максимальная скорость будет у слоя в центре трубы. Такое течение жидкости, при котором отдельные слои между собой не перемешиваясь, движутся с различными скоростями называется ламинарным. Распределение скоростей при ламинарном течении имеет параболический характер (рис.3.2,а). акое течение можно условно разделить на слои: слой молекул, прилегающий к стенке трубы, прилипает к ней, и остается практически неподвижен. Каждый последующий слой молекул, смещаясь относительно предыдущего слоя, двигается по отношению к стенке трубы с постепенно возрастающей скоростью. Максимальная скорость будет у слоя в центре трубы. Такое течение жидкости, при котором отдельные слои между собой не перемешиваясь, движутся с различными скоростями называется ламинарным. Распределение скоростей при ламинарном течении имеет параболический характер (рис.3.2,а).
Ламинарное течение является стационарным течением. При увеличении скорости течения жидкости в ней появляются перепады давления и частицы из периферийных слоев, где давление больше, переходят в центральные, где давление меньше. В результате этого слои перемешиваются, образуются завихрения, скорости течения частиц беспорядочно меняются. Такое течение жидкости является нестационарным и называется турбулентным (рис.3.2,б). При турбулентном течении существенно меняется структура потока, оно сопровождается шумом.
Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы и определяется числом Рейнольдса (Rе):
Rе=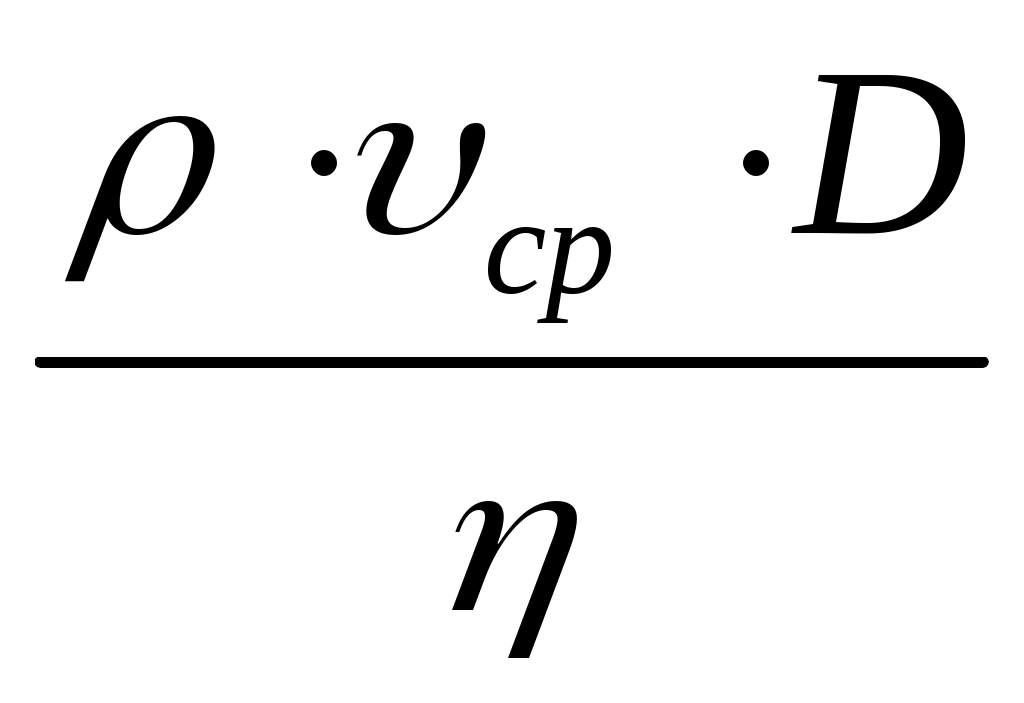 , (3.9) , (3.9)
где D – диаметр трубы, ср– средняя скорость течения жидкости, - плотность жидкости, - коэффициент вязкости.
Турбулентность возникает при стационарном течении ньютоновских жидкостей, когда число Рейнольдса превышает критическое значение Rекрит, т.е. RеRекрит. При ReReкрит – течение ламинарное. Критическое число Рейнольдса одинаково для всех стационарных течений при данной геометрии трубы. Так, при течении жидкости в круглой трубе постоянного сечения критическое число Рейнольдса Reкрит2000.
Течение крови по большинству сосудов кровеносной системы в норме является ламинарным. Турбулентность возможна лишь в начале аорты, в местах разветвления крупных сосудов, а также при их стенозировании. Шум, возникающий при турбулентном течении крови, может быть использован при диагностике заболеваний.
3.5 Течение вязкой жидкости по трубе. Закон Гагена-Пуазейля и его использование в гемодинамике.
При течении по горизонтальной трубе реальной жидкости потенциальная энергия ее частиц расходуется на работу по преодолению внутреннего трения, поэтому статическое давление вдоль трубы постепенно падает. Для того, чтобы обеспечить течение жидкости, необходимо в начале трубы создать давление, несколько превышающее падение давления вдоль всей трубы, т.е. для течения жидкости по трубе необходимо создать разность давлений (Р1-Р2) на концах трубы.
Гаген и Пуазейль сначала эмпирически, а затем теоретически установили, что средняя скорость ср ламинарного течения ньютоновской жидкости по горизонтальной, круглой трубе постоянного сечения прямо пропорциональна разности давлений (P1-P2) на концах трубы, квадрату радиуса трубы R2и обратно пропорциональна коэффициенту вязкости жидкости и длине трубы l (закон Гагена-Пуазейля):
ср=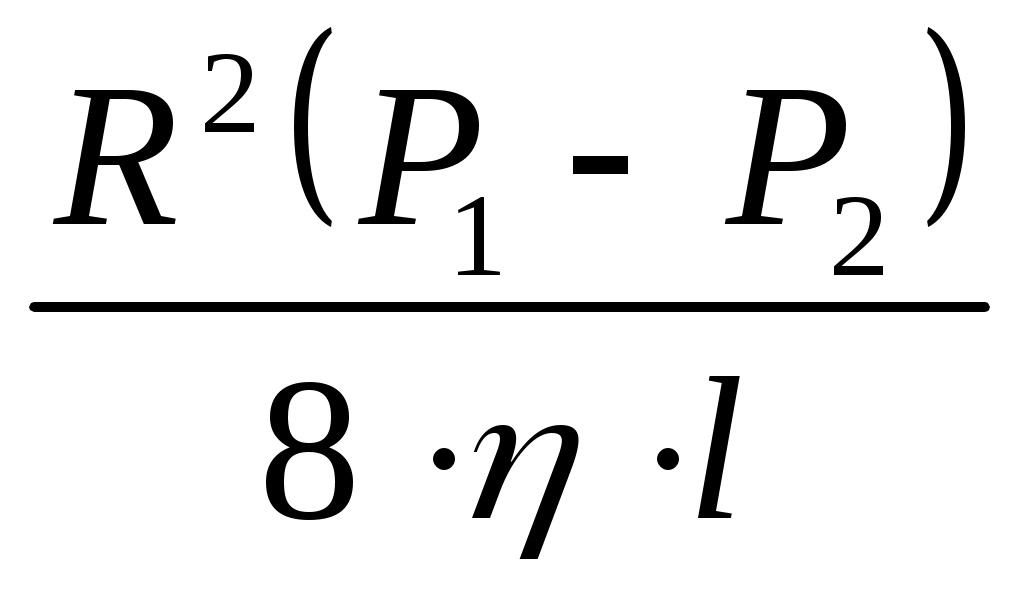 (3.10) (3.10)
Эта формула выражает аналитически закон Гагена-Пуазейля для средней линейной скорости жидкости.
Подставляя в уравнение (3.7) выражение (3.10) и, учитывая, что S=R2, получим:
Q=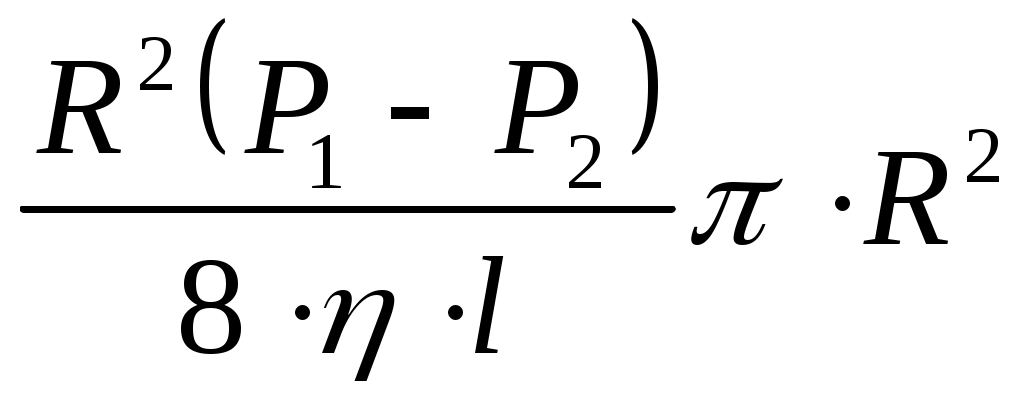 = =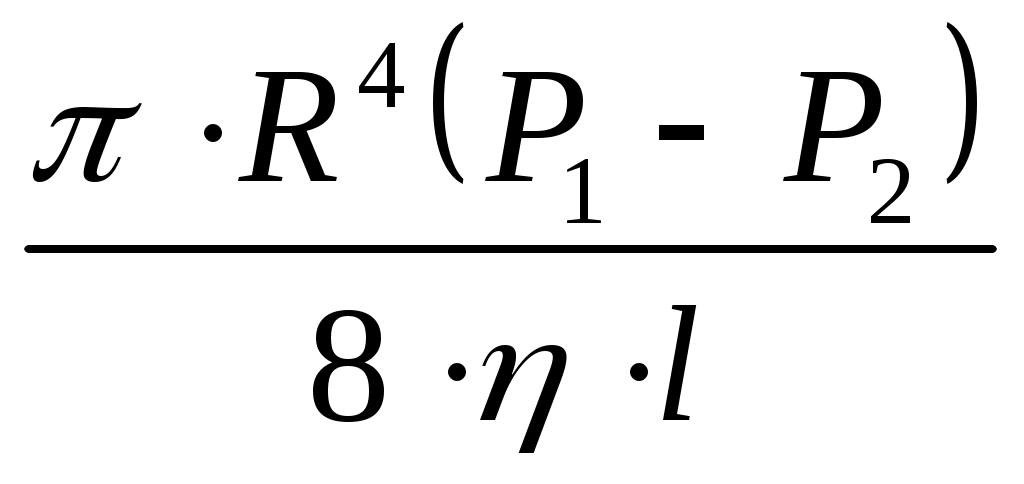 (3.11) (3.11)
Уравнение (3.11) выражает закон Гагена-Пуазейля для объемной скорости течения жидкости.
Напомним, что кровь по своей природе является неньютоновской жидкостью. Однако, учитывая, ее небольшую вязкость, кровь в первом приближении относят к ньютоновским жидкостям. В связи с этим, закон Гагена-Пуазейля применим для описания движения крови. В этом случае ср называют средней линейной скоростью кровотока, а Q– объемной скоростью кровотока.
О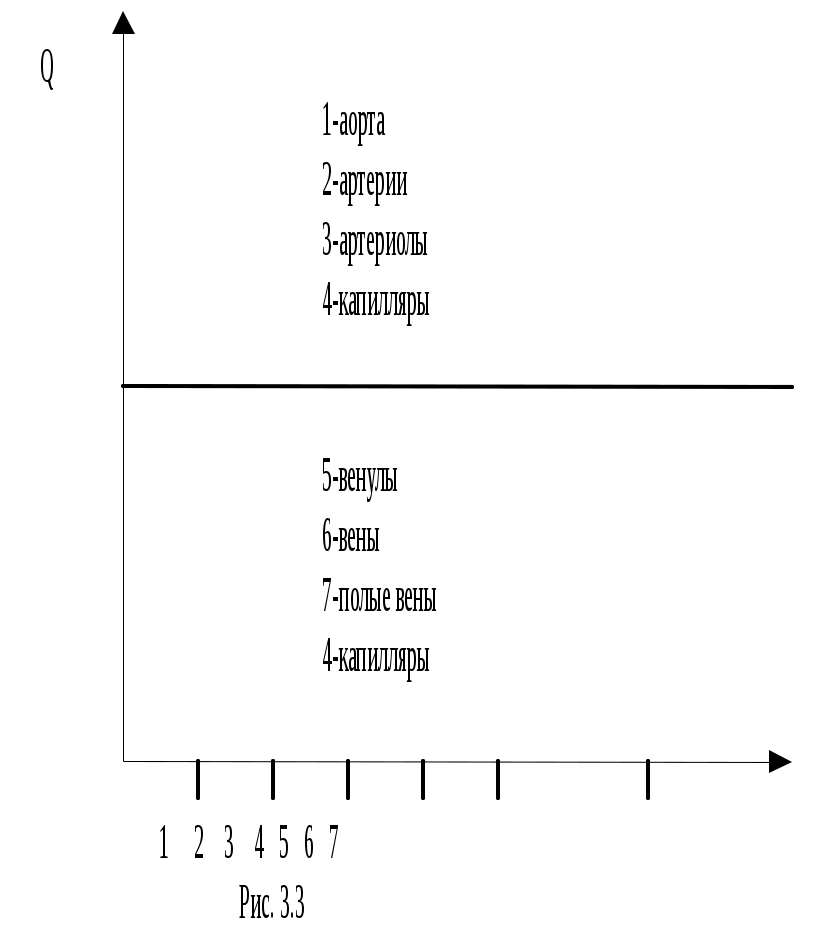 бъемная скорость кровотока– это есть минутный объем крови. У человека, находящегося в покое, объемная скорость кровотока Q составляет 55.5 л/мин. Это значит, что у человека в состоянии покоя, объем крови, протекающий за 1 минуту через поперечное сечение аорты, всех артерий или артериол, капилляров, венозную систему как большого так и малого круга кровообращения одинаков (рис.3.3). бъемная скорость кровотока– это есть минутный объем крови. У человека, находящегося в покое, объемная скорость кровотока Q составляет 55.5 л/мин. Это значит, что у человека в состоянии покоя, объем крови, протекающий за 1 минуту через поперечное сечение аорты, всех артерий или артериол, капилляров, венозную систему как большого так и малого круга кровообращения одинаков (рис.3.3).
При постоянной объемной скорости кровотока, средняя линейная скорость кровотока ср не может быть постоянной. Согласно условию стационарного течения, она зависит от поперечного сечения S: чем больше S, тем меньше ср. Учитывая суммарное поперечное сечение, самым широким местом в сосудистой системе является отдел капилляров: суммарное поперечное сечение капилляров в 500-600 раз больше поперечного сечения аорты. Поэтому кровь в капиллярах двигается в 500-600 раз медленнее, чем в аорте. С этой точки зрения, аорта является самым узким местом в сосудистой системе и, соответственно, средняя линейная скорость кровотока в аорте максимальная и составляет
0.5 м/с (рис.3.7).
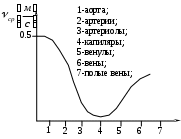
Рис. 3.4
В полых венах средняя скорость кровотока составляет (0.25-0.3) м/с, т.к. суммарное поперечное сечение вен по отношению к поперечному сечению аорты увеличивается в 2 раза, а по отношению к капиллярам – уменьшается.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Чем обусловлена вязкость жидкости (или внутреннее трение)?
Что характеризует градиент скорости? В каких единицах измеряется?
Какие жидкости относятся к ньютоновским (неньютоновские)?
Каковы реологические свойства крови и что на них влияет?
Что называется стационарным течением вязкой жидкости?
Что называется объемной скоростью кровотока? В каких единицах измеряется?
Какое течение называется ламинарным (турбулентным)?
От чего зависит средняя линейная скорость ламинарного течения ньютоновской жидкости по горизонтальной трубе исходя из уравнения Гагена-Пуазейля?
Укажите график зависимости объемной скорости кровотока вдоль сосудов большого (или малого) круга кровообращения?
Укажите график зависимости линейной скорости кровотока вдоль сосудов большого (или малого) круга кровообращения?
|
 Скачать 364.5 Kb.
Скачать 364.5 Kb.