геодезия. Лекция 2 ГЕОДЕЗИЯ. 1 2 Земной эллипсоид и его основные элементы. Общий земной эллипсоид и референцэллипсоид, требования к ним. Уровенные поверхности и их свойства.
 Скачать 285 Kb.
|
|
1.1.2 Земной эллипсоид и его основные элементы. Общий земной эллипсоид и референц-эллипсоид, требования к ним. Уровенные поверхности и их свойства. Геоид и квазигеоид.. Основные линии и плоскости земного эллипсоида: экватор, параллель, меридиан. Нормальные сечения эллипсоида, главные нормальные сечения. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, длины дуг меридианов и параллелей. Взаимные нормальные сечения и геодезическая линия ------------------------------------------------------------------------------------------------------------------------------------------------------------------------ Земной эллипсоид и его основные элементы. Общий земной эллипсоид и референц-эллипсоид, требования к ним. Фигура Земли – фигура ограниченная физической поверхностью Земли, т.е. поверхность твердой оболочки и не возмущенной поверхностью морей и океанов. Из-за сложности геоида (эта поверхность математически не выражается), принимают поверхность эллипсоида вращения – близкой по форме к геоиду, но математически правильной поверхности, на которую можно перенести результаты измерений выполненных на физической поверхности Земли. 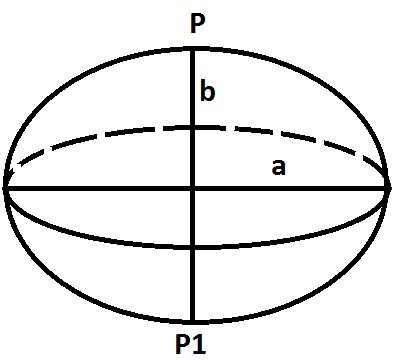 Земной Эллипсоид – это фигура, образованная в результате вращения эллипса вокруг его малой оси РР1. Характеризуется параметрами: а - большой полуосью и в – малой полуосью, сжатием:  .Вместо сжатия может быть использован эксцентриситет эллипсоида  .Различают общеземной эллипсоид, который наилучшим образом согласуется с поверхностью геоида в целом и референц-эллипсоид, который наилучшим образом согласуется с геоидом на ограниченной части его поверхности. Общеземной эллипсоид - эллипсоид имеющий наибольшую близость к фигуре Земли. Параметры общеземного эллипсоида определяются условиями: 1) Центр эллипсоида должен совпадать с центром масс Земли, а его малая полуось с осью вращения Земли 2) Объем эллипсоида должен быть равен объему геоида 3) Сумма квадратов отклонений по высоте поверхности эллипсоида от поверхности геоида должна быть минимальной. Для определения этих параметров выполняются градусные измерения, которые изначально сводились к определению длины дуги меридиана в 10 градус, а в настоящее время превратились в сложный комплекс астрономо-геодезических, гравиметрических и спутниковых измерений с привлечением данных из других смежных наук В течение полутора веков ученые разных стран занимались определением параметров земного эллипсоида, используя доступные им результаты градусных измерений. Итогом этих определений служит появление ряда эллипсоидов, наиболее известные из которых представлены в табл. 1.1. Таблица 1.1 Параметры наиболее известных земных эллипсоидов
В каждой стране принимают в качестве рабочего тот эллипсоид, который наилучшим образом подходит для ее территории. В соответствии с этим критерием выполняют и его ориентирование в теле Земли, т.е. определение координат начального пункта. Такие рабочие эллипсоиды, используемые в разных странах, называются референц-эллипсоидами. В СССР и ряде стран восточной Европы принят референц-эллипсоид Красовского, 1940 г. Эллипсоид Красовского является наиболее точным из всех эллипсоидов, полученных из обработки наземных измерений. Его размеры близки к размерам ОЗЭ, найденным по данным наблюдений ИСЗ. ------------------------------------------------------------------------------------------- Уровенные поверхности и их свойства Уровенная поверхность - поверхность, всюду перпендикулярная отвесным линиям(поверхность равного потенциала силы тяжести и представляет собой фигуру равновесия жидкого или вязкого вращающегося тела, образующегося под действием сил тяжести и центробежных сил.) Свойства уровенных поверхностей: Уровенные поверхности можно проводить на разных высотах, все они являются замкнутыми и почти параллельны одна другой. Через одну точку пространства проходит только одна уровенная поверхность. Направление нормали к уровенной поверхности совпадает с направлением силы тяжести, то есть с отвесной линией. Форма уровенной поверхности не имеет точного математического выражения и зависит от распределения масс различной плотности в теле Земли. Одна из уровенных поверхностей гравитационного поля Земли — Геоид ------------------------------------------------------------------------------------------------------------- Геоид и квазигеоид Геоид – эквипотенциальная поверхность земного поля тяжести. (Уровенная поверхность поля силы тяжести Земли, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии (перпендикулярная к направлению силы тяжести в любой её точке.)) Для точного определения поверхности геоида какой-либо точки необходимо выполнить комплекс измерений, непосредственно на поверхности геоида. Что практически не возможно, либо в соответствующей точке на физической поверхности Земли с учетом распределения масс в этом месте, что также не предоставляется возможным. По этой причине было предложено вместо поверхности геоида использовать квазигеоид. В теории М.С. Молоденского в качестве вспомогательной вводится поверхность квазигеоида, совпадающая с геоидом на океанах и морях и весьма мало отступающая от поверхности геоида на суше (менее 2м). В отличие от геоида поверхность квазигеоида может быть строго определена по результатам наземных наблюдений. Основные линии и плоскости земного эллипсоида: экватор, параллель, меридиан. При определении положения точек на поверхности Земли и на поверхности земного эллипсоида пользуются некоторыми линиями и плоскостями. Известно, что точки пересечения оси вращения земного эллипсоида с его поверхностью являются полюсами, один из которых называется Северным Рс, а другой – Южным Рю 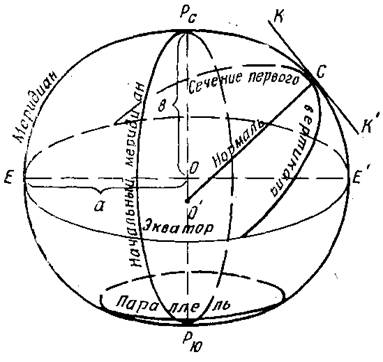 рис.1 Сечения земного эллипсоида плоскостями, перпендикулярными к малой его оси, образуют след в виде окружностей, которые называются параллелями. Параллели имеют различные по величине радиусы. Чем ближе расположены параллели к центру эллипсоида, тем больше их радиусы. Параллель с наибольшим радиусом, равным большой полуоси земного эллипсоида, называется экватором. Плоскость экватора проходит через центр земного эллипсоида и делит его на две равные части: Северное и Южное полушария. Кривизна поверхности эллипсоида является важной характеристикой. Она характеризуется радиусами кривизны меридианного сечения и сечения первого вертикала, которые называются главными сечениями Сечения поверхности земного эллипсоида плоскостями, проходящими через его малую ось (ось вращения), образуют след в виде эллипсов, которые называются меридианными сечениями. На рис. прямая СО', перпендикулярная к касательной плоскости КК' в точке ее касания С, называется нормалью к поверхности эллипсоида в этой точке. Каждая нормаль к поверхности эллипсоида всегда лежит в плоскости меридиана, а следовательно, пересекает ось вращения эллипсоида. Нормали к точкам, лежащим на одной параллели, пересекают малую ось (ось вращения) в одной и той же точке. Нормали к точкам, расположенным на разных параллелях, пересекаются с осью вращения в различных точках. Нормаль к точке, расположенной на экваторе, лежит в плоскости экватора, а нормаль в точке полюса совпадает с осью вращения эллипсоида. Плоскость, проходящая через нормаль, называется нормальной плоскостью, а след от сечения этой плоскостью эллипсоида – нормальным сечением. Через любую точку на поверхности эллипсоида можно провести бесчисленное множество нормальных сечений. Меридиан и экватор являются частными случаями нормальных сечений в данной точке эллипсоида. Нормальная плоскость, перпендикулярная к плоскости меридиана в данной точке С, называется плоскостью первого вертикала, а след, по которой она пересекает поверхность эллипсоида, – сечением первого вертикала. Взаимное положение меридиана и любого нормального сечения, проходящего через точку С (рис. 2) на данном меридиане, определяется на поверхности эллипсоида углом А, образованным меридианом данной точки С и нормальным сечением. 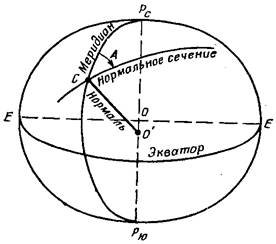 Этот угол называется геодезическим азимутом нормального сечения. Он отсчитывается от северного направления меридиана по ходу часовой стрелки от 0 до 360°. Если принять Землю за шар, то нормаль к любой точке поверхности шара пройдет через центр шара, а любая нормальная плоскость образует на поверхности шара след в виде окружности, которая называется большим кругом. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны. Через нормаль к поверхности эллипсоида можно провести множество плоскостей. Эти плоскости называются нормальными. Кривые, образуемые от пересечения нормальных плоскостей в данной точке, с поверхностью эллипсоида, называются нормальными сечениями. В каждой точке на поверхности эллипсоида есть два взаимно перпендикулярных сечения, кривизна которых имеет максимальное и минимальное значение. Эти нормальные сечения называются главными нормальными сечениями. В 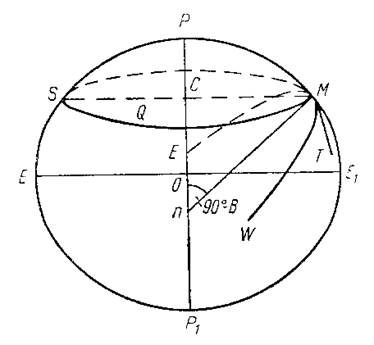 точке М поверхность эллипсоида вращения главными нормальными сечениями будут меридианное сечение точки М и сечение первого вертикала. Эти два сечения представляются эллипсами. Сечение первого вертикала, проходящее через точку М, будет перпендикулярно меридианному сечению точки М.Обозначим через M и N радиусы кривизны меридиана и первого вертикала. Не приводя выводы формул, запишем:   , где: a – большая полуось эллипсоида; e – первый эксцентриситет эллипсоида; B – геодезическая широта точки M. Из формул видно, что радиусы кривизны возрастают при увеличении широты. Запишем отношение N и M. 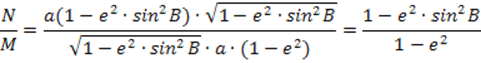 Н 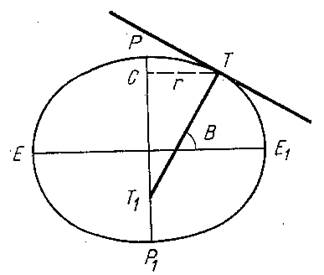 а полюсе B=90˚, поэтому на полюсе M и N будут равны. Во всех остальных случаях N больше M. Если меридиан имеет меньший радиус, то кривизна наибольшая. Радиусом кривизны первого вертикала является отрезок нормали ТТ1.Средним радиусом кривизны в данной точке поверхности называется предел, к которому стремится среднее арифметическое из радиусов кривизны нормальных сечений, когда число их стремится к бесконечности. Для точек эллипсоида средний радиус кривизны Rравен среднему геометрическому из радиусов кривизны главных нормальных сечений, меридиана и первого вертикала, проведенных для той же точки.  Радиус кривизны меридиана применяют при вычислении длин дуг меридианов и разности широт. Разность кривизны первого вертикала применяют при вычислении длин дуг параллелей, разности долгот и азимутов. Средний радиус кривизны применяют, когда Землю принимают за шар; при вычислении сферических избытков и других случаях. Если TT1 радиус кривизны первого вертикала, а r – радиус кривизны параллели, проходящей через точку T, то  Вычисление длин дуг меридианов и параллелей. Пусть требуется определить длину дуги меридиана между точками A и C с широтами B1 и B2. Разобьем этот отрезок дуги на бесконечно малые отрезки, тогда дуга малого отрезка выразится формулой  , как малый отрезок дуги окружности радиуса M.Д  лина всей дуги Ac определится из интегрирования функции 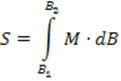 в пределах от B1 до B2: В триангуляции, при длинах дуг свыше 45 км используется формула:  Здесь: Mm – радиус кривизны меридиана для средней широты  Для длин дуг менее 45 км можно воспользоваться формулой: 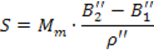 ,это означает, что длину дуги можно определить, как дугу центрального угла окружности равном B2-B1. Длина дуги параллели (окружности) определяется формулой:  , где  .Понятие о взаимных нормальных сечениях и геодезической линии. Возьмем на поверхности эллипсоида две точки A и B, не лежащие на одном меридиане с широтами BA и BС. Широта BС >BA. Проведем нормали в точках A и B. Нормали не пересекаются, так как лежат в разных плоскостях. Широты BA и BСне равны, значит нормали пересекают малую ось эллипсоида в разных местах. Нормаль с более северной широтой пересекает малую ось южнее, чем нормаль с меньшей широтой. П 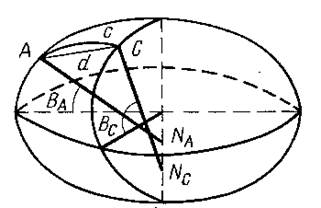 лоскость, проходящая через нормаль ANA и точку C, не совпадает с плоскостью, проведенной через нормаль CNC и точку A. Первая плоскость образует с поверхностью эллипсоида нормальное сечение AAC, вторая нормальное сечение CCA. Между двумя точками поверхности эллипсоида проходят два нормальных сечения, которые называются взаимными нормальными сечениями. Сечение AAC прямое, а сечение CCA обратное в точке A.Если начальная точка A лежит южнее точки C, то прямое нормальное сечение точки A отклоняется к югу от обратного. Прямое нормальное сечение можно представить, если в точке A установить теодолит, чтобы его вертикальная ось совпадала с нормалью, то при визировании на вторую точку C, выставленные в створе вешки, обозначат прямое нормальное сечение на поверхности эллипсоида. При измерении на земной поверхности вертикальная ось теодолита устанавливается по отвесной линии, в то время как прямое нормальное сечение является стороной триангуляции, полигонометрии на поверхности эллипсоида. Значит, при проектировании на поверхность эллипсоида надо вводить поправки за уклонение отвесных линий и за высоту наблюдаемой цели над поверхностью эллипсоида. В равнинных районах принимают измеренные направления на поверхности Земли такими же и на поверхности эллипсоида. Если по измеренным направлениям составить треугольники, то стороны следует изобразить взаимно обратными нормальными сечениями. Значит, на поверхности эллипсоида не образуется замкнутой фигуры. В  еличина угла Δ между взаимными нормальными сечениями небольшая и зависит от длины линии S, ее азимута A и широты B. Так при B=60˚, A=50˚ при: · S=30 км Δ=0,004" · S=100 км Δ=0,032" При положении пунктов на одном меридиане или на одной параллели взаимные нормальные сечения сливаются в одну линию. В триангуляции 2,3,4 класса двойственностью нормальных сечений пренебрегают. В триангуляции 1 класса двойственность нормальных сечений устраняют тем, что пункты соединяют геодезическими линиями. Геодезическая линия – это кривая, являющаяся кратчайшим расстоянием между двумя точками на поверхности эллипсоида. Геодезическая линия в точках A и C располагается к прямым нормальным сечениям и составляет с ним угол δ равный 1/3 Δ. | |||||||||||||||||||||||||||||||||||