5-СхЗерт. 1 3 лабораториялы жмыс. Саба таырыбы Логиканы негізгі ымдары Саба масаты
 Скачать 1.88 Mb.
|
Сабақ тақырыбы: Математикалық логиканың ЭЕМ теориясына қолданылуыСабақ мақсаты: Математикалық логиканың айтылымдарының екілік санау жүйесіндегі екілік цифрларға сәйкестігі және ЭЕМ-нің екі позициялық элементтерімен схемаларының сәйкестігі компьютердің әртүрлі құрылғыларының жұмысын алгебралық логикалық символика көмегімен сипаттауға мүмкіндік береді. Математикалық логиканың аппараты ЭЕМ теориясының негізгі екі есебін шығаруға қолданылады. Кез келген дайын схеманың жұмысын логикалық алгебра функциясымен сипаттауға болады. Бұдан кейін өрнекті түрлендіре отырып, схеманың тиымдылығын тексеріп, элементтер санын азайтып, бастапқы схеманың қызметін толық атқаратын, яғни схеманың қызметін толық атқаратын, яғни схеманың функциясын қанағаттандыратын ықшамдалған схема алу қарастырылады. Жұмысты орындауға арналған әдістемелік нұсқау: Әрбір айырып-қосқыштың тек екі күйі: тұйықталған және ажыратылған күйі бар. Х айырып-қосқышына сәйкес ол тұйықталған кезде ғана, яғни тоқ өткізетін кезде 1 мәнін, ал ажыратылған кезде ( тоқ жүрмейтін кезде) 0 мәнін қабылдайтын логикалық айнымалысын х әрпімен белгілейміз. Енді Х және айырып-қосқыштарының қатынасын Х қосылғанда айырып-қосқышы қосылғанда айырып-қосқышы ажыратылады деп қабылдайық.. Сонда Х айырып-қосқышына х логикалық айнымалысы, ал айырып-қосқышына логикалық айнымалысы сәйкес болады. Бүкіл айырып-қосқыш схеманың қызметін толық анықтай алатын, бүкіл айырып-қосқыш схемаға сәйкес болатын, х және логикалық айнымалыларына тәуелді бір функцияны өрнектеуге болады. Әрбір айырып-қосқыштық схеманы өрнектейтін мұндай функция өткізгіштік функциясы деп аталады. Кейбір айырып-қосқыш схемалардың F өткізгіштік функцияларын анықтайық.: a) Схемада айырып-қосқыш болмағандықтан F=1; б) Схема тұрақты ажыратылған айырып-қосқыштан тұратындықтан F=0; в) х айырып-қосқышы тұйықталса схема тоқ өткізеді де, ажыратылса тоқ өткізбейді, сондықтан F(x) = x; г) Схема айырып-қосқышы ажыратылса тоқ өткізеді де, тұйықталса тоқ өткізбейді, сондықтан F(x) = ; д) Тапсырмалар:Берілген есептің схемасын құрастырыңыз: 1. Схема x және y екі айырып-қосқыштары бірдей тұйықталса ғана тоқ өткізеді, сондықтан F(x) = x . y; 2. Схема x және y екі айырып-қосқыштарының ең болмаса біреуі тұйықталса да тоқ өткізеді, сондықтан F(x)=x v y; 3. Төрт айырып-қосқыш ( x, y, z және t) схемасы бар, тоқты тек t айырып-қосқышы тұйықталғанда және қалған үш айырып-қосқыштың біреуі тұйықталғанда ғана өткізетін схеманы құрастыру керек. 4. Бес айырып-қосқыштың төртеуі тұйықталғанда ғана тоқ өткізетін схеманы құрастыру керек 5. Схеманың өткізгіштік функциясын табу екрек: 6. Мына айырып-қосқыш схеманы ықшамдайық: а) 7 Мына айырып-қосқыш схеманы ықшамдайық:. 8. Мына айырып-қосқыш схеманы ықшамдайық: 9 Мына айырып-қосқыш схеманы ықшамдайық. Тапсырманың бағалануы:Осы лабораториялық жұмысты толық және қатесіз орындпғандар жалпы – 5 балмен бағаланады. Пайдалынған әдебиеттер: Н.В.Макарова, Е.Л.Рамин и др. Основы схемотехники: Сборник задач. Под. ред. Н.В.Макаровой.- М.: Финансы и статистика, 1997. Информатика и программирование на ЭВМ. Алматы: КазГАСА, 1996 С.Мюллер. Ремонт и модерниаци ПК. Москва Санкт-Петербург. Киев 2004г. В.С.Янпольский. Основы автоматики и вычислительной техники. Москва. «Просвещение» 1991 г. Гришкун В.В. Организация компьютеризированного обучения на базе иерархических структур данных. – Алматы, 1996. Акимов О.Е. Дискретная математика. – Комосмольск-на-Амуре, 1996. № 12- 15 лабораториялық жұмыс. Сабақ тақырыбы: Логикалық сызбалар мен функциялар. Сабақ мақсаты: Логикалық сызбаны зерттеу Логикалық элементтер көмегімен логикалық функцияларды жүзеге асыру Берілген логикалық функцияларды орындайтын логикалық сызбаларды талдау Жұмысты орындауға арналған әдістемелік нұсқау: Құралдар және элементтер Логикалық түрлендіргіш Сөз генераторы Вольтметр. Логикалық тексергіштер + 5в кернеуінің көзі «логикалық бірлік» сигналының көзі Екі позициялық ауыстырып-қосқыш Екікірмелі элементтер ЖӘНЕ, ЖӘНЕ-ЕМЕС, НЕМЕСЕ, НЕМЕСЕ-ЕМЕС 74 сериясының микросызбасы. Теориядан қысқаша мағлұматтар 1. Логика алгебрасының аксиомалары. Логика алгебрасында қарастырылатын айнымалылар тек екі мәнді ғана қабылдай алады - 0 немесе 1. Логика алгебрасында мыналар анықталған: эквиваленттік қатынас («=» белгісімен белгіленеді) және амалдар: белгісімен белгіленетін бөлу (дизъюнкциялар), & немесе нүктемен белгіленетін көбейту (конъюнкциялар), және үстіңгі сызықпен немесе апострофпен белгіленетін терістеу (немесе инверсиялар), Логика алгебрасы төмендегі аксиомалар жүйесімен анықталады: 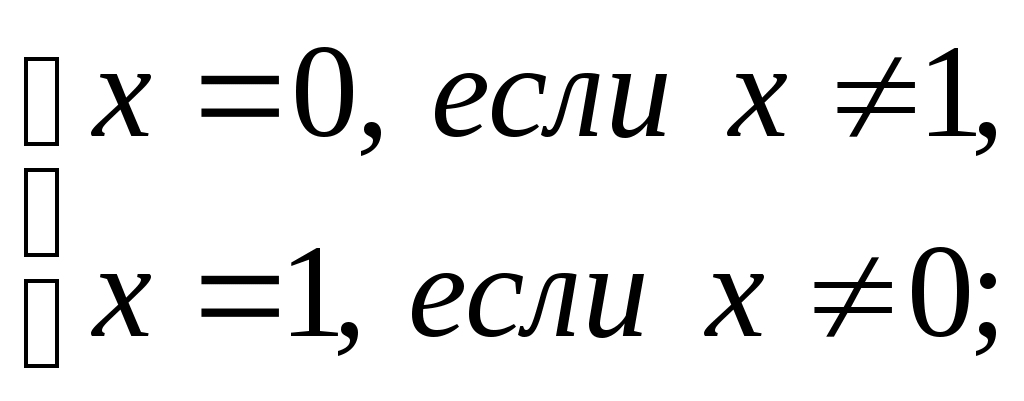 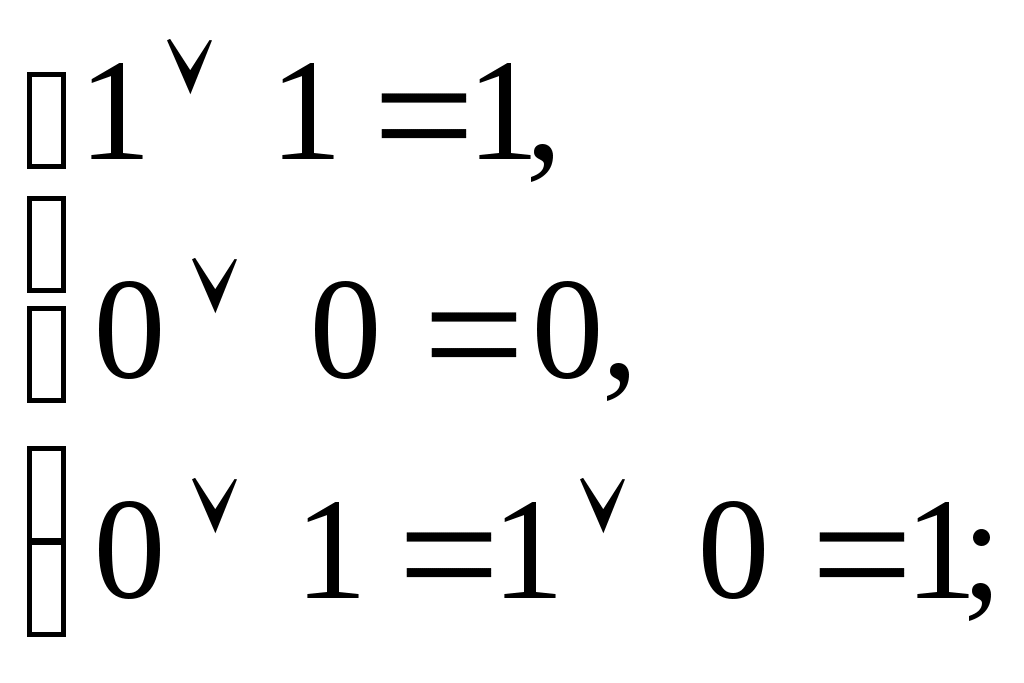 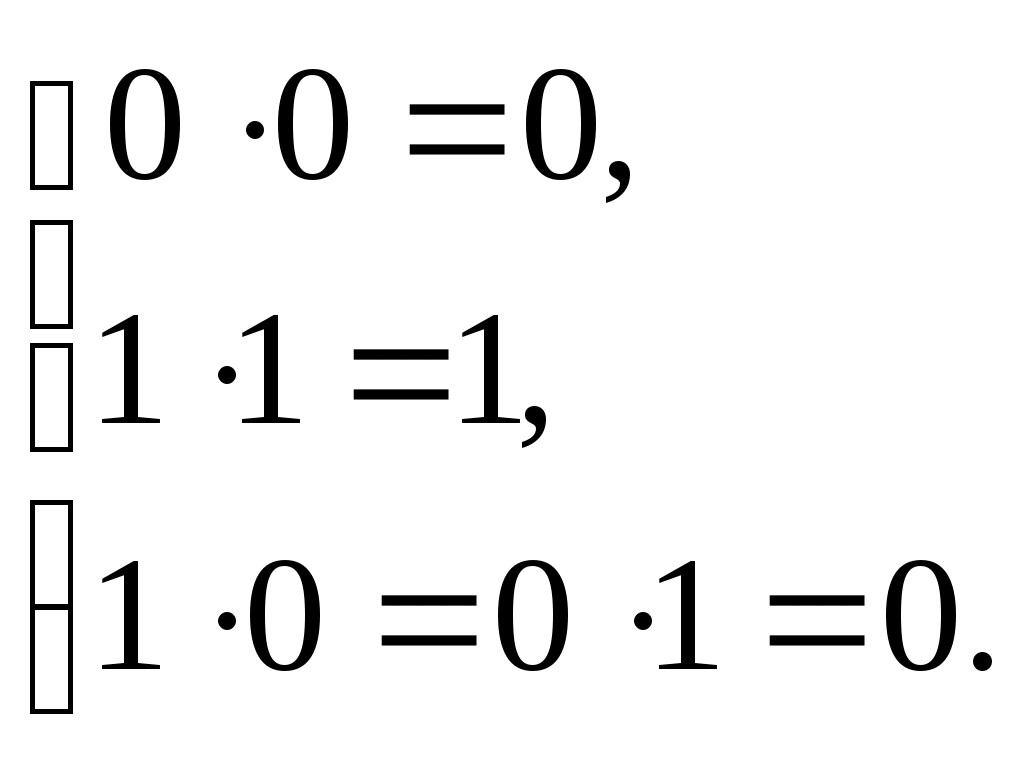  2. Логикалық формула Логикалық формулаларды жазу әдетте конъюнктивті немесе дизъюнктивті қалыпты формаларда жүзеге асады. Дизъюнкциялық формада логикалық формулалар логикалық өрнектердің логикалық суммасы түрінде жазылады, конъюнкциялық формада – логикалық сумманың логикалық көбейтіндісі түрінде жазылады. Іс-әрекет реті кәдімгі алгебралық өрнектердегі сияқты. Логикалық өрнектер логикалық функцияның мағынасын логикалық айнымалының мағынасымен байланыстырады. 3. Логикалық тепе-теңдіктер. Логикалық өрнектерді түрлендіруде логикалық тепе-теңдіктер қолданылады.: 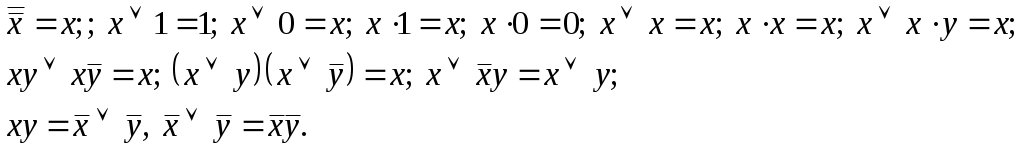 4. Логикалық функциялар  айнымалыларынан тұратын кез келген өрнекті логика алгебрасындағы амалдардың соңғы санының көмегімен п айнымалысының кейбір функциялары сияқты қарастыруға болады. Осындай функцияны логикалық деп атайды. Логика алгебрасының аксиомаларына сәйкес айнымалы мәніне байланысты функция 0 немесе 1 мәнін қабылдай алады. Логикалық айнымалылардың n функциясы 2nайнымалы мәндері үшін п екілік разрядты санының барлық мүмкін мәндеріне сәйкес анықталады. х және у айнымалыларының негізгі функциялары төменде келтіріледі. f1(х, у) = х· у – логикалық көбейту (конъюнкция), f2(x, у) = х v у – логикалық бөлу (дизъюнкция), f3(x, у) =  - логикалық көбейтуді терістеу, f4(x, у) =  - логикалық бөлуді терістеу, f5(x, у) =  - 2 модулі бойынша суммасын табу, f6(x, у) =  - тепе-теңдік равнозначность. Логикалық сызбалар Логика алгебьрасының амалдарының біреуін немесе қарапайым логикалық функцияны жүзеге асыратын физикалық құрылғы логикалық элемент деп аталады. Анықталған ереже бойынша логикалқ элементтердің соңғы санынан құрылған сызба логикалық сызба деп аталады. Негізгі логикалық функцияларға оларды орындап жатқан сызба элементтері сәйкес келеді . Ақиқат кестесі. Анықталу облысы сияқты п айнымалысының кез келген функциясы шекті (2п мәні), мұндай функция i= 0,1 ... 2n-1 орналасқан Vi нүктесінде қабылайтын f(Vi) мәндер кестесінде берілуі мүмкін. Мұндай кестені ақиқат кестесі деп атайды. 12.1 кестесінде жоғарыда көрсетілген функциялырды беретін ақиқат кестесі көрсетілген. Кесте 12.1
i = 2х+у – айнымалы мәндерімен түрленген сан. Тапсырмалар: Тәжірибе1. ЖӘНЕ логикалық функциясын зерттеу. а). Логикалық сигнал дәрежелерінің берілуі 1 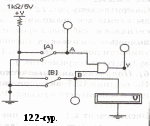 2_01 ден 12.2 суретте бейнеленген сызбасы бар файлды ашыңыз. Бұл сызбада А және В екі екіпозициялы ауыстырып-қосқыштарды 0 (ауыстырып –қосқыш байланысы төменгі жағдайда)немесе 1(ауыстырып –қосқыш байланысы төменгі жағдайда) дәрежесіндегі ЖӘНЕ логикалық сызбасының кірісіне береді. Сызбаны іске қосыңыз. В ауыстырып-қосқышын төменгі жағдайға орнатыңыз. В-ға кіретін кернеуді вольтметрмен өлшеңіз және логикалық тексергіш көмегімен логикалық сигнал дәрежесін анықтаңыз. В ауыстырып-қосқышын жоғарғы жағдайға орнатыңыз. Логикалық сигнал дәрежесін анықтаңыз және вольтметр көреткішін жазыңыз: Y шығысында қандай сигнал формаланатынын көрсетіңіз. Нәтижесін «эксперимент нәтижелері» бөліміне жазыңыз. Б) ЖӘНЕ элементінің ақиқаттық кестесін тәжірибе бойынша алу: С 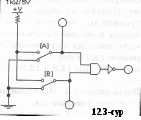 ызба кірісіне А және В сигнал дәрежелерінің барлық мүмкін қисындасуларын беріңіз және әр қисындасу үшін Y шығатын сигналының дәрежесін жазып қойыңыз. ЖӘНЕ логикалық сызбасының ақиқаттық кестесін толтырыңыз. ("Тәжірибе нәтижелері" бөліміндегі 12.4 кесте). в). Функция үшін талдау формуласын алу 12.4 кестесі бойынша ЖӘНЕ элементі функциясының талдау формуласын құрыңыз және оны «эксперимент нәтижелері» бөліміне жазыңыз. Тәжірибе 2. ЖӘНЕ-ЕМЕС логикалық функциясын зерттеу. а). 2ЖӘНЕ және ЕМЕС элементтерінен құрылған 2ЖӘНЕ және ЕМЕС элементінің ақиқаттық кестесін тәжірибе бойынша алу: 12.3. суретте бейнеленген сызбаларды жинаңыз. Сызбаны іске қосыңыз. Сызба кірісіне сигнал дәрежелерінің барлық мүмкін қисындасуларын беріңіз және логикалық шығыс пен кірістегі сигналдарды байқай отырып, тексергіш көмегімен 2ЖӘНЕ және ЕМЕСлогикалық сызбасының ақиқаттық кестесін толтырыңыз("Тәжірибе нәтижелері" бөліміндегі 12.5 кесте). б)2ЖӘНЕ және ЕМЕС логикалық элементінің ақиқаттық кестесін тәжірибе бойынша алу: 1 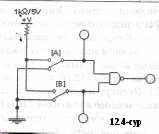 2.4. суретте бейнеленген сызбаларды жинаңыз. Сызбаны іске қосыңыз. Сызба кірісіне сигнал дәрежелерінің барлық мүмкін қисындасуларын беріңіз және логикалық шығыс пен кірістегі сигналдарды байқай отырып, тексергіш көмегімен 2ЖӘНЕ және ЕМЕСлогикалық сызбасының ақиқаттық кестесін толтырыңыз("Тәжірибе нәтижелері" бөліміндегі 12.6 кесте). 12.5 және 12.6 кестелерін бір-бірімен салыстырыңыз.Тәжірибе 3. НЕМЕСЕ логикалық функциясын зерттеу. А) НЕМЕСЕ логикалық элементінің ақиқаттық кестесін тәжірибе бойынша алу: 12.5. суретте бейнеленген сызбаларды жинаңыз. Сызбаны іске қосыңыз. Сызба кірісіне сигнал дәрежелерінің барлық мүмкін қисындасуларын беріңіз және логикалық шығыс пен кірістегі сигналдарды байқай отырып, тексергіш көмегімен НЕМЕСЕ логикалық сызбасының ақиқаттық кестесін толтырыңыз("Тәжірибе нәтижелері" бөліміндегі 12.7 кесте). б 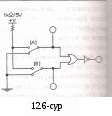 ). Функция үшін талдау формуласын алу. 12.7 кестесі бойынша функцияның талдау формуласын құрыңыз және оны «эксперимент нәтижелері» бөліміне жазыңыз. Тәжірибе 4. НЕМЕСЕ-ЕМЕС логикалық функциясын зерттеу а). 2НЕМЕСЕ және ЕМЕС элементтерінен құрылған 2ЖӘНЕ және ЕМЕС элементінің ақиқаттық кестесін тәжірибе бойынша алу: 12.6. суретте бейнеленген сызбаларды жинаңыз. Сызбаны іске қосыңыз. Сызба кірісіне сигнал дәрежелерінің барлық мүмкін қисындасуларын беріңіз және логикалық шығыс пен кірістегі сигналдарды байқай отырып, тексергіш көмегімен 2НЕМЕСЕ және ЕМЕСлогикалық сызбасының ақиқаттық кестесін толтырыңыз("Тәжірибе нәтижелері" бөліміндегі 12.8 кесте). б)2ЖӘНЕ және ЕМЕС логикалық элементінің ақиқаттық кестесін тәжірибе бойынша алу: 12.7. суретте бейнеленген сызбаларды жинаңыз. Сызбаны іске қосыңыз. Сызба кірісіне сигнал дәрежелерінің барлық мүмкін қисындасуларын беріңіз және логикалық шығыс пен кірістегі сигналдарды байқай отырып, тексергіш көмегімен 2НЕМЕСЕ және ЕМЕСлогикалық сызбасының ақиқаттық кестесін толтырыңыз("Тәжірибе нәтижелері" бөліміндегі 12.9 кесте). 12.8 және 12.9 кестелерін бір-бірімен салыстырыңыз. Тәжірибе 5. Логикалық сызбаларды сөз генераторларының көмегімен зерттеу зерттеу а). Зерттелетін сызба жайлы мағлұмат. 12_02 ден 12.8 суретте бейнеленген сызбасы бар файлды ашыңыз. Сызбаны іске қосыңыз. 7400 микросызбасының қандай шығысына қоректену көзі жалғанатынын, микросызбада қанша 2ЖӘНЕ-ЕМЕС бар екенін, осы тәжірибеде неше элемент қолданылатынын және сызбада шығыстар мен кірістер қалай белгіленіп тұрғанын көрсетіңіз. Микросызба жайлы мағлұмат кестесін толтырыңыз ("Тәжірибе нәтижелері" бөліміндегі 12.10 кесте). б)2ЖӘНЕ және ЕМЕС логикалық элементінің ақиқаттық кестесін тәжірибе бойынша алу: Сөз генераторын генератор шығысында келесі комбинациялар ретін: 00, 01, 10 алатындай етіп бағдарламалаңыз. 11. Генератордың үлкейтілген бейнесінің артында орналасқан "Step" батырмасын басу арқылы генераторды қадамдық жұмыс режиміне ауыстырыңыз. "Step" батырмасының әр басылуы генератордың шығысына берген берілген реттіліктің келесі сөзіне көшуді орындайды. Микросызбаға берілген реттіліктен сөздерді рет-ретімен бере отырып, 2ЖӘНЕ-ЕМЕС элементінің ақиқаттық кестесін толтырыңыз. ("Тәжірибе нәтижелері" бөліміндегі 12.11 кесте). Ескерту: генератор шығысында ағымдағы сөз разрядының мәндері генератор панелінің төменгі бөлігінде дөңгелек терезелерде бейнеленеді. Тәжірибе 6. Логикалық сызбаларды сөз генераторларының көмегімен зерттеу. Үш айнымалының логикалық функциясын жүзеге асыру. а).Логикалық формуламен берілген функцияны орындайтын сызбаны талдау. 2ЖӘНЕ-ЕМЕС элементтеріндегі f = аb v bс функциясын жүзеге асырыңыз.. Ескерту: Логикалық көбейту мен терістеу амалдары арқылы функция формуласын көрсетіңіз 2ЖӘНЕ-ЕМЕС элементтеріндегі алынған формулаларға сәйкес сызбаларды Electronics Workbench-ке жинаңыз. Сызба кірісіне сөз генераторын, шығысына логикалық тексергішті қосыңыз. Сөз генераторын 0 ден 7-ге дейінгі сандарға сәйкес, сегіз сөзден тұратын реттілікті формалауға бағдарламалаңыз. 0=000; 1=001; 2=010; 3=011; 4=100; 5=101; 6=110; 7=111. Қадамдық режимде, алынған сызбаның кірісіне барлық сөздерді рет-ретімен бере отырып, логикалық тексергіштің көмегімен сызбаның шығысындағы сигнал дәрежесін анықтаңыз.Алынған нәтижелер бойынша Тәжірибе нәтижелері бөліміндегі 12.12 кестесін толтырыңыз. б). Логикалық түрлендіргіш көмегімен берілген фуенкцияны орындайтын сызбаны талдау. f=аb v bс логикалық формуласымен сипатталған функццияны орындап жатқан сызбаны алу үшін, логикалық түрлендіргішті пайдалануға болады. Ол үшін төмендегілерді орындаңыз: Логикалық түрлендіргішті шақырыңыз Түрлендіргіш панелінің төменгі терезесіне аb v bслогикалық формуласын пернетақтадан енгізіңіз (НЕМЕСЕ амалына + белгісі сәйкес келеді, терістеу апострофпен белгіленеді.); ЖӘНЕ-ЕМЕС элементтеріндегі сызбаны жүзеге асыру үшін логикалық түрлендіргіш панеліндегі AIBNAND батырмасын басыңыз Логикалық түрлендіргіш енгізілген логикалық өрнекпен сипатталған, функцияны жүзеге асыратын сызбаны жұмыс алаңына шығарады. Алынған сызба 12.9. суретте бейнеленген. Сызбаға 0 ден 7-ге дейінгі сандарға сәйкес, сегіз сөзден тұратын реттілікті формалауға бағдарламаланған сөз генераторын қосыңыз. 0=000; 1=001; 2=010; 3=011; 4=100; 5=101; 6=110; 7=111. С 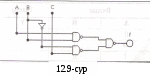 өз генераторын қадамдық режимге ауыстырыңыз. Сызбаны іске қосыңыз. Сызба кірісіне көрсетілген сөздерді рет-ретімен бере отырып және сызба шығысындағы сигнал дәрежесін логикалық текусергіш көмегімен анықтай отырып, ақиқаттық кестесін толтырыңыз("Тәжірибе нәтижелері" бөліміндегі 12.13 кесте).Екі аралықтағы мәндерді анықтап, оларды ақиқаттық кестесіне жазыңыз. ("Тәжірибе нәтижелері" бөліміндегі 12.13 кесте). Олар сызбадағы үшінші 2ЖӘНЕ-ЕМЕС элементінің кірісіндегі логикалық сигналдарын анықтайды(есептеу нәтижелерін бақылау үшін оның кірісіне логикалық тексергіштерді қосуға болады.) Тапсырманың бағалануы:Осы лабораториялық жұмысты толық және қатесіз орындпғандар жалпы – 5 балмен бағаланады. Пайдалынған әдебиеттер: Н.В.Макарова, Е.Л.Рамин и др. Основы схемотехники: Сборник задач. Под. ред. Н.В.Макаровой.- М.: Финансы и статистика, 1997. Информатика и программирование на ЭВМ. Алматы: КазГАСА, 1996 С.Мюллер. Ремонт и модерниаци ПК. Москва Санкт-Петербург. Киев 2004г. В.С.Янпольский. Основы автоматики и вычислительной техники. Москва. «Просвещение» 1991 г. Гришкун В.В. Организация компьютеризированного обучения на базе иерархических структур данных. – Алматы, 1996. Акимов О.Е. Дискретная математика. – Комосмольск-на-Амуре, 1996. аветисян Р.Д. Теоретические основы информатики. – М.: 1997. Громов А.И. Основы информатики и вычислительной техники. – М.:1994. 9. Схематехника негіздері Оқу-әдістемелік кешен. Ж.А. Мүсіралиев, Ж.Ж.Қожамқұлова.- Алматы: ҚазМемҚызПИ, 2006.- 68 б. № 16- 18 лабораториялық жұмыс. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||