Контрольная по метрологии. 1. 5 Погрешности измерений и си
 Скачать 345.75 Kb. Скачать 345.75 Kb.
|
|
1.5 Погрешности измерений и СИ Совокупность свойств, обуславливающих получение результата с требуемыми точности характеристиками в необходимом виде и установленные сроки, определяют качество измерений.  Точность измерений отражает близость результата к истинному значению измеряемой величины. Достоверность измерений характеризует степень доверия к результатам измерения и определяется на основе законов теории вероятностей и математической статистики, что в свою очередь дает возможность для каждого конкретного случая выбирать средство и методы измерений, обеспечивающие получение результата, погрешности которого не превышают заданных границ. Правильность результатов измерений – это качество измерений, отражающее близость к нулю систематических погрешностей в результатах. Прецизионность результатов – степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях. Зависит только от случайных факторов и не связано с истинным значением измеряемой величины. Прецизионность включает в себя сходимость и воспроизводимость результатов измерений. Сходимостью называется качество измерений, отражающее близость друг к другу результатов, полученных в одинаковых условиях. Сходимость также отражает влияние случайных погрешностей. Воспроизводимость – качество измерений, которое отражает близость друг к другу результатов измерений, выполненных в различных условиях. Классификация погрешностей измерения 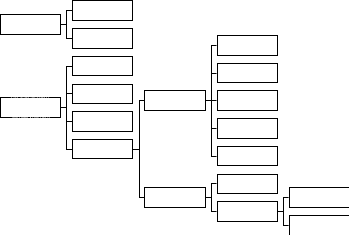 09.11.2021 г. Классификация инструментальных погрешностей (средств измерения)  Абсолютная погрешность - разность результата измерения (показаний прибора Хп) и действительного Хд значения измеряемой величины: 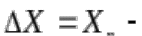 Относительная погрешность - отношение абсолютной погрешности к действительному значению измеряемой величины 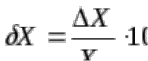 Точность результата измерения - параметр, характеризующий близость результата измерения к истинному (действительному) значению измеряемой величины  Приведенная погрешность - отношение абсолютной погрешности к нормирующему значению Хn 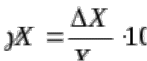 В качестве нормирующего значения используются: 1) Разница верхнего и нижнего пределов шкалы, если шкала прибора равномерная с нулевой отметкой на краю или в середине шкалы; 2) Разница верхнего и нижнего пределов, равномерного участка шкалы, если вся шкала имеет неравномерный характер 3) Если в технической документации на средство измерения указывается номинальное значение измеряемой величины, то это номинальное значение используется в качестве нормирующего независимо от шкалы прибора. Номинальная функция преобразования – это функция, которая приписана измерительному устройству данного типа, указана в его паспорте и используется при выполнении с его помощью измерений. Реальная функция преобразования – это функция, которая обладает отдельной конкретный экземпляр измерительного устройства данного типа. Аддитивная погрешность (или погрешность нуля) – возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (остается постоянной при всех значениях измеряемой величины). 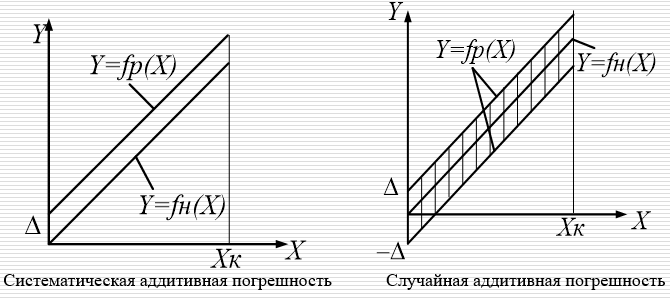 Мультипликативная погрешность (или погрешность чувствительности) – погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины. 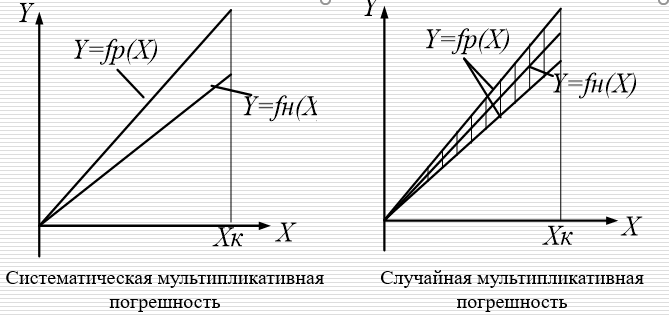 Погрешностью линейности - называют несовпадение номинальной и реальной функций преобразования, вызванное нелинейными эффектами. 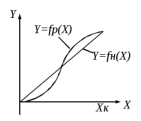 Погрешность гистерезиса или погрешность обратного хода – несовпадение номинальной и реальной функций преобразования при прямом и обратном ходе (при постепенном увеличении и постепенном уменьшении измеряемой величины). 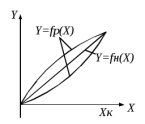 16.11.2021 г. Нормирование метрологических характеристик Все рассмотренные ранее характеристики измерительных устройств, а также их погрешности, принято называть метрологическими, т.к они влияют на точность получаемого результата. Путем нормирования метрологических характеристик (примечание: далее – МХ) обеспечивается взаимозаменяемость средств измерений (далее – СИ) и единства измерений. Нормирование МХ заключается в установлении границ для отклонений реальных значений параметров СИ от их номинальных значений. Нормирование погрешностей СИ производится по максимально допускаемым значениям основной и дополнительной погрешностям. Согласно стандарту, пределы этих погрешностей выражают в приведенной, относительной или абсолютной формах, в зависимости от характера изменения погрешности в пределах диапазона (аддитивный, мультипликативный или смешанный). Пределы абсолютной основной погрешности нормируются для измерительных мер в единицах измеряемой величины или в делениях шкалы. Способы нормирования основной погрешности определяются ее постоянством и простотой процедуры нормирования. Нормирование основной погрешности (способы): Если абсолютная погрешность Δ(х) является мультипликативной, то относительная погрешность при любом х будет величиной постоянной:  Ее используют для нормирования погрешности и указания класса точности в виде γs. Тогда граница относительной погрешности результата измерений: 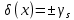 Абсолютная погрешность результата измерения: 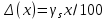 При аддитивной полосе погрешности для любых значений х граница абсолютной погрешности: 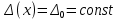 Нормируют не абсолютное Δ0, а приведенное значение этой погрешности: 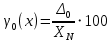 – аддитивная приведенная погрешность – аддитивная приведенная погрешностьТекущее значение относительной погрешности обратно пропорционально х: 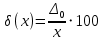 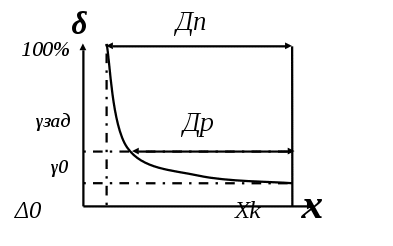 Только для однопредельного средства измерений!!! Относительная погрешность равна приведенной аддитивной погрешности 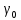 только на верхнем пределе шкалы. только на верхнем пределе шкалы.Значение измеряемой величины х=Δ0 при котором 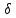 (Δ0)=100% называется порогом чувствительности СИ. (Δ0)=100% называется порогом чувствительности СИ.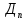 – диапазон показаний; – диапазон показаний;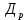 – рабочий диапазон при заданной относительной погрешности. – рабочий диапазон при заданной относительной погрешности.В случае если измерительные устройства являются многопредельным, то 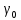 указывают только для нижнего диапазона, чем ниже диапазон, тем ниже точность. указывают только для нижнего диапазона, чем ниже диапазон, тем ниже точность.  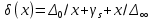  – подставляется в относительных единицах не в процентах – подставляется в относительных единицах не в процентах0 и ∞ - нижний и верхний пороги чувствительности 23.11.2021 г. При смешанном характере полоса абсолютной погрешности D(x) описывается соотношением и имеет форму трапеции: 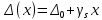 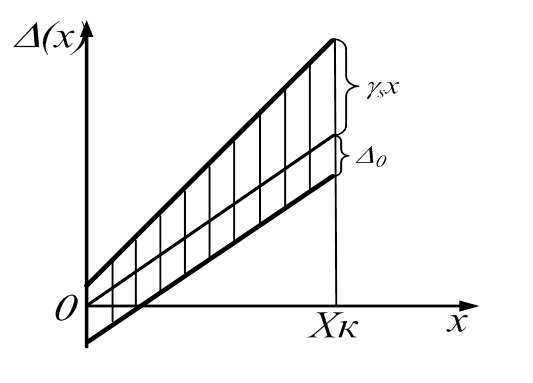 Если уравнение разделить на предел измерения Xк, то для приведенного значения погрешности получим: 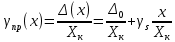 Обозначив приведенное значение погрешности в начале диапазона через 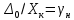 Для приведенного значения погрешности:  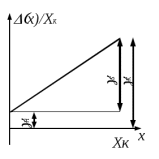 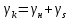 Для измерительных устройств со смешанным характером погрешности нормируют приведенные погрешности в конце и начале диапазона 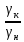 . .Тогда относительная погрешность результата измерения (в %) определяется по формуле:  Нормирование дополнительной погрешности Дополнительная погрешность устанавливается в виде постоянного значения для всей рабочей области влияющей величины. Путем указания отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины к этому интервалу. Путем указания функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния. Может быть указана зависимостью предела допускаемой дополнительной погрешности от влияющей величины: 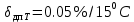 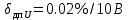 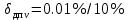 Инструментальная погрешность в рабочих условиях определяется суммированием пределов допускаемых значений погрешностей (основных и дополнительных):  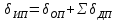 Класс точности Λ - обобщенная характеристика СИ, определяемая границами допускаемой основной и дополнительной погрешностей, а также рядом других свойств, влияющих на точность измерений. Обозначение классов точности на средствах измерения Согласно ГОСТ 8.401-80 (переиздан 2010 г.) для указания нормированных значений: погрешности чувствительности γs, приведенной аддитивной погрешности γ0, приведенных погрешностей γн и γк могут использоваться числа из ряда 6; 5; 4; 2,5(3); 2; 1,5(1,6); 1,0 10n, где n = 1, 0, -1, -2 и т.д., выраженные в %. Если класс точности (Λ) установлен по значению погрешности чувствительности γs, обозначаемое на шкале значение класса точности обводится кружком. Например: Λ = 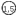 означает, что γs = означает, что γs = 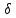 (x) = 1,5% (x) = 1,5%2. Если класс точности (Λ) установлен по значению приведенной аддитивной погрешности γ0, то на шкале обозначается двумя способами: 1,5 или  Например: 1,5 - означает, что γ0=γпр=1,5% для всего диапазона измерений;  - означает, что γ0=γпр=1,5% для равномерного участка неравномерной шкалы. - означает, что γ0=γпр=1,5% для равномерного участка неравномерной шкалы.Обозначение класса точности (Λ) в виде 0,02/0,01 указывает, что погрешность прибора нормирована по двучленной формуле с γн=0,01% и γк=0,02%: 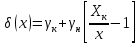 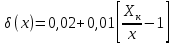 Выбор СИ При выборе необходимых устройств необходимо учитывать: 1. Допустимое значение погрешности, установленные в НТД; 2. Допустимое отклонение влияющих величин; 3. Условия проведения измерений; 4. Методы проведения измерений и способы контроля; 5. Соответствие средств измерений требованиям достоверности; 6. Номинальные значения измеряемой величины 7. Требования к габаритам, массе и конструкции СИ. Общие принципы выбора СИ: Для гарантированно заданной или расчетной относительной погрешности измерения относительная погрешность СИ должна быть на 25-30% ниже 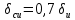 Если известна приведенная погрешность, то 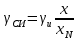 Цена деления шкалы должна выбираться с учетом заданной точности измерения Рабочий участокшкалы СИ должен выбираться по правилу: относительная погрешность в пределах него не должна превышать приведенную погрешность более чем в 3 раза: при односторонней равномерной шкале с 0 отметкой в начале рабочий участок занимает 2/3 длины шкалы; при двусторонней шкале с 0 отметкой посередине – последнюю 1/3 каждого сектора; При шкале без 0 – рабочий участок может распространяться на всю длину шкалы. 30.11.2021 г. 1.7 Функции распределения результатов измерений и случайных погрешностей Интегральная функция распределения случайной величины X– функция вида: 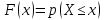  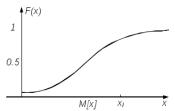 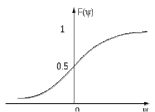 Производная от функции распределения – плотность распределения случайной величины:  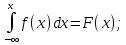 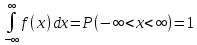    Условие нормирования плотности распределения 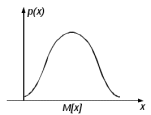   Дисперсия Мат. ожидание Для оценки результатов измерений используются центральные моменты: 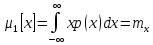 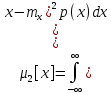 Нормальный закон распределения Плотность вероятности p(X) для закона нормального распределения случайной величины Х: 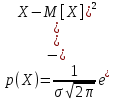 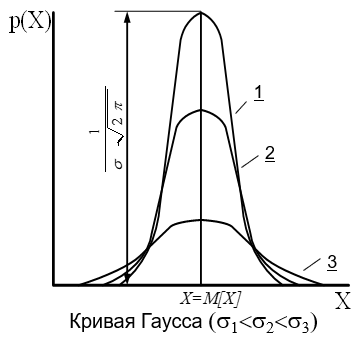 Доверительным интервалом называют интервал, который с заданной доверительной вероятностью накрывает истинное значение измеряемой величины. Вероятность P попадания результата измерения (случайной погрешности) в заданный интервал [а;в] для нормального распределения: 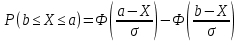 Значения функции Лапласа табулированы. Обработка результатов измерений Обработка результатов многократных равноточных прямых измерений: 1. Исключение промахов из результатов измерений; 2. Исключение систематической погрешности: - Введение поправок; - Подбор квалифицированного персонала; - Исключение воздействия влияющих величин; - Выбор наиболее точного метода измерения; - Приведение условий эксперимента к нормальным. 3. Определение истинного значения измеряемой величины 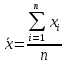 4. Определение среднеквадратичного отклонения 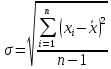 5. Проверка гипотезы о нормальности распределения результатов наблюдения - при n > 50 – критерий Пирсона; - при 15 < n < 50 – критерий Колмогорова; - при n < 15 – проверка не производится. 6. Исключение грубых погрешностей   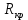 определяется по таблицам для заданного уровня значимости (доверительной вероятности) определяется по таблицам для заданного уровня значимости (доверительной вероятности) 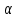 и числа наблюдений n (числа степеней свободы). и числа наблюдений n (числа степеней свободы).В лабораторных измерениях доверительная вероятность принимается 0,95 или 95%, уровень значимости 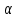 0,05 или 5%. 0,05 или 5%.Если какое-либо из условий не выполняется, то производится отбрасывание соответствующих максимальных либо минимальных, либо обоих значений и осуществляется пересчет, начиная с 3-го пункта. 7. Запись окончательного результата в виде доверительного интервала с учетом правила округления 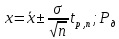 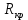 и и 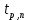 выбираются по таблицам для заданной вероятности выбираются по таблицам для заданной вероятности 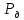 и числа измерений n. и числа измерений n.Округление результата начинается с погрешности, если первая значащая цифра «1» или «2», то до двух значащих цифр, если «3» и более, то до одной значащей цифры. До того же разряда, что и погрешность, округляется истинное значение. Если погрешность больше 9, то выносится общий множитель, а затем производится округление. Методика обработки результатов косвенных измерений Если величина Z является функцией Z = f (a, b, c,…)и определяется на основании прямых измерений величин a, b, c,… Истинное значение косвенной величины Z является функцией  где 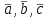 - истинные значения прямых измерений - истинные значения прямых измеренийДля случая многократных косвенных измерений определяют среднюю квадратичную погрешность, которая вычисляется по следующей формуле: 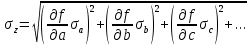 где  , , 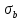 , , 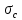 - среднеквадратические погрешности - среднеквадратические погрешностиВ случае однократных прямых измерений абсолютная погрешность косвенного результата может быть определена: 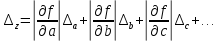 Где  – абсолютные погрешности результатов прямых измерений. – абсолютные погрешности результатов прямых измерений.Относительная погрешность косвенного измерения определяется: 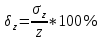 (или (или 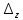 – в случае, если измерения однократные) – в случае, если измерения однократные) |
