Задачи по механике (Иродов). 1. 60. Гладкий резиновый шнур, длина которого L и коэффициент упругости k, подвешен одним концом к точке О. На другом конце имеется упор В.

• Название: 1. 60. Гладкий резиновый шнур, длина которого L и коэффициент упругости k, подвешен одним концом к точке О. На другом конце имеется упор В.
• Дата: 18.06.2019
• Размер: 443 Kb.
• Имя файла: Задачи по механике (Иродов).doc
• Тип: Документы; #82263

1
.60. Гладкий резиновый шнур, длина которого l и ко­эффициент упругости k, подвешен одним концом к точке О. На другом конце имеется упор В. Из точки О начинает свободно падать муфта А массы т. Пренебрегая лассой шнура и упора, найти максимальное растяжение шнура.

Решение.

Выберем за нулевой уровень потенциальной энергии точку, в которой растяжения шнура максимальное. Тогда, в точке О муфта имела потенциальную энергию

.

В точке В после растяжения шнура на максимальную величину x муфта получила потенциальную энергию силы упругости шнура:

.

По закону сохранения энергии имеем:



Из двух вариантов решения выбираем знак «+», т.к. только в этом случае получаем положительное растяжение шнура. Таким образом, максимальное растяжение шнура равно:

.
1.61. Тело массы т пустили вверх по наклонной плоскости, составляющей угол  с горизонтом. Начальная скорость тела равна v₀,коэффициент трения между телом и плоскостью k. Какой путь пройдет тело до остановки и какова на этом пути работа силы трения?

Решение.

П
о второму закону Ньютона имеем:

.

Спроектируем это уравнение на оси координат, показанные на рисунке:



Сила трения скольжения равна:

F_m = kN; N = mg cos.; F_m = k mg cos..

Тогда из первого уравнения проекций закона Ньютона на оси координат имеем:

–k mg cos. – mg sin.= ma  –k g cos. – g sin.= a.

Считая движение до остановки равнозамедленным, запишем ускорение тела:

.

Тогда получаем выражения для искомого пути, которое пройдет тело до остановки:

.

Работа силы трения на данном пути равна:


1.62. Цепочка ле­жит на столе, свеши­ваясь у его края на = 1/4своей длины. Масса цепочки
m= 1,00 кг,ее длина l= 1,5 м,коэффициент трения покоя между столом и цепочкой k = 0,20. Действуя на конец А некоторой горизонтальной силой F, свешивающуюся часть цепочки медленно втянули на стол. Какую работу совершила при этом сила F?



Решение.

Сила F совершает работу по преодолению силы трения для участка цепочки, лежащего на столе, и силы тяжести для участка цепочки, который свешивается вниз. В процессе втягивания участок действия силы трения изменяется от (1 – )l до l, а участок действия силы тяжести изменяется от l до 0. Тогда получаем выражения для работы сил трения и тяжести:



Соответственно работа данной силы F равна полученной работе по модулю и противоположна по знаку, т.е.

Дж.

1.63. Тело массы т бросили под углом  к горизонту с начальной скоростью v₀. Найти среднюю мощность, развиваемую силой тяжести за все время полета, и мгновенную мощность этой силы как функцию времени.

Решение.



Траекторией движения является парабола. В силу симметрии работа силы тяжести при поднимании тела на максимальную высоту равна по модулю и противоположна по знаку работе силы тяжести при опускании тела, т.е. . Время подъема на максимальную высоту равно времени опускания тела: . Тогда, средняя мощность, развиваемая силой тяжести за все время полета, равна:



Мгновенная мощность, которую развивает сила равна:

.

Разложим скорость на составляющие вдоль оси x и вдоль оси y:

.

Поскольку составляющая скорости вдоль оси x перпендикулярна к направлению силы тяжести F= mg, то она не дает вклад в мощность силы тяжести. Поэтому рассматриваем только составляющую скорости вдоль оси оси y.

Имеем выражение для мощности, развиваемую силой тяжести, как функцию времени:

.

1.64. Материальная точка массы т движется по окружности радиусом Rс нормальным ускорением, которое меняется со временем по закону w_n= at², где а – постоянная Найти зависимость от времени мощности всех сил, действующих на эту точку, а также среднее значение этой мощности за первые секпосле начала движения.

Решение.

Мощность всех сил, действующих на эту точку, равна:

.

Работа всех сил равна изменению кинетической энергии точки за первые tсекпосле начала движения:

.

Из выражения для нормального ускорения получаем:

.

Тогда работа всех сил равна:

.

Зависимость мощности от времени равна: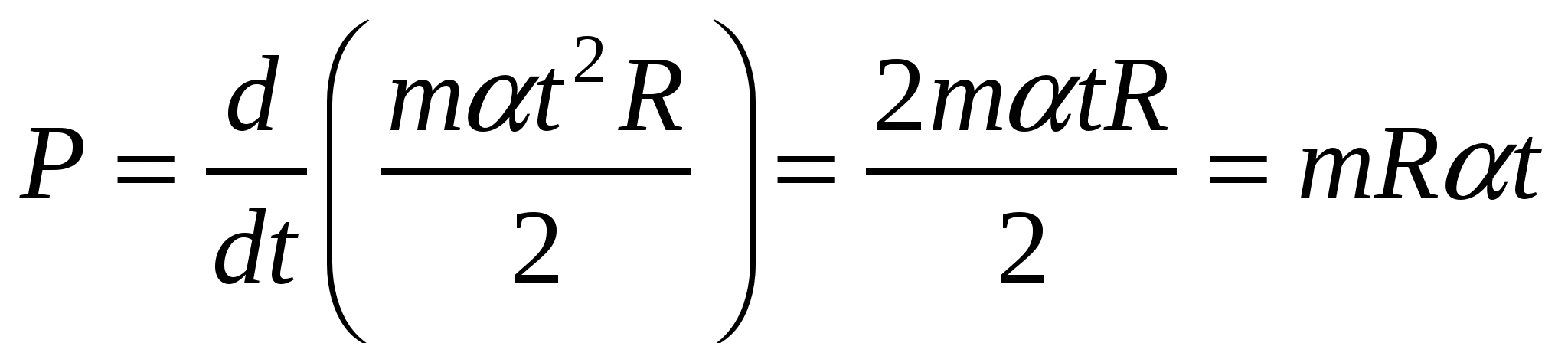

.

Среднее значение мощности за первые секпосле начала движения равно:

.


1.65. Небольшое тело массы т находится на горизонтальной поверхности в точке О. Телу сообщили горизонтальную скорость v₀. Найти:

а) среднюю мощность, развиваемую силой трения завсе время движения, если коэффициент трения k = 0,27; m = 1,0 кг и v₀ = 1,5 м/с;

б) максимальную мгновенную мощность силы трения, если коэффициент трения меняется по закону k= x, где  – постоянная, х – расстояние от точки О.

Решение.

а) Средняя мощность, развиваемая силой трения завсе время движения, равна:

,

где – средняя скорость движения тела от начальной скорости до остановки.

Сила трения направлена против направления движения, поэтому ее проекция на это направления равна:

.

Тогда получаем:

Вт.

б) Мощность силы трения равна:

.

Работа силы трения равна:



Тогда, мгновенная мощность равна:



С другой стороны работы силы трения равна изменению кинетической энергии тела:



Тогда имеем:



Тогда, мгновенная мощность равна:

.

Для нахождения максимальной мощности, исследуем полученное выражение на экстремум:



Подставим полученное значение в выражение для мгновенной мощности: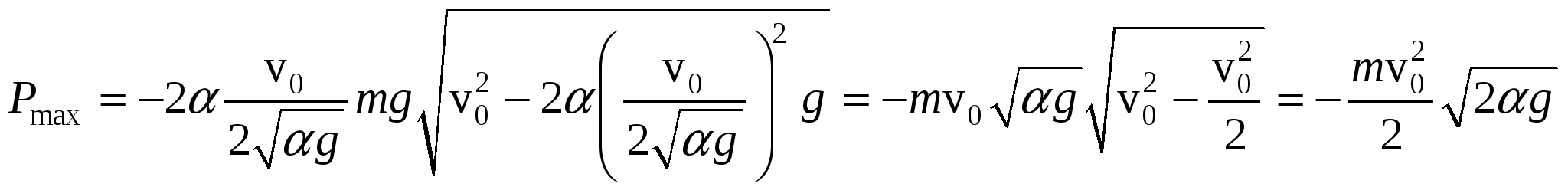

.


1.66. В системе отсчета, вращающейся вокруг неподвижной оси с постоянной угловой скоростью ₀= 5,0 рад/секдвижется небольшое тело массы m = 0,10 кг.Какую работу совершила центробежная сила инерции при перемещении этого тела из точки 1 в точку 2,если точки находятся на расстояниях r₁ =30 сми r₂ = 50 смот оси вращения?

Решение.

Центробежная сила инерции направлена к центру вращения. Ее работа при перемещении тела из точки 1 в точку 2, расположенных на разных расстояниях от центра вращения, равна изменению кинетической энергии тела:

.

Связь между линейной и угловой скоростями дается соотношением:

.

Тогда работа центробежной силы инерции равна:

Дж.


1.67. К_с - система отсчета, в которой покоится центр инерции механической системы взаимодействующих материальных точек, движется поступательно со скоростью V относительно инерциальной К-системы отсчета. Масса механической системы равна m, ее полная энергия в К_с- системе отсчета Е_с. Найти полную энергию Е данной механической системы в К-системе отсчета.

Решение.

Энергия системы взаимодействующих материальных точек в К-системе отсчета равна сумме кинетических энергий всех точек, входящих в систему:



Скорость точки в К-системе отс+чета равна:

v_k = V + v_{k c},

где v_kc – скорость точки в К_с-системе отсчета

Тогда получаем:

.

Выражение равно массе всей системы; выражение равно энергии механической системы в К_с- системе отсчета; , где V_С – скорость центра инерции системы в К_с- системе отсчета. Тогда получаем:

.

Поскольку в К_с- системе отсчета центр масс системы покоится, то V_С = 0. Тогда получаем полную энергию Е данной механической системы в К-системе отсчета:

.

1.68. На гладкой горизонтальной плоскости находятся две небольшие шайбы с массами m₁ и m₂, которые соединены между собой пружинкой. В некоторый момент времени шайбам сообщили начальные скорости v₁ и v₂. Оба вектора взаимно перпендикулярны, лежат в горизонтальной плоскости и один из них совпадает по направлению с прямой, проходящей через центры шайб. Пренебрегая массой пружинки, найти полную энергию этой механической системы в поступательно движущейся системе отсчета, связанной с ее центром инерции.

Решение.

Энергия этой механической системы есть сумма кинетических энергий ее тел:

.

Введем вектор взаимного расстояния шайб:

.

Поместим начало координат в центре инерции, что дает:

.

Из двух последних равенств находим:


Тогда получаем: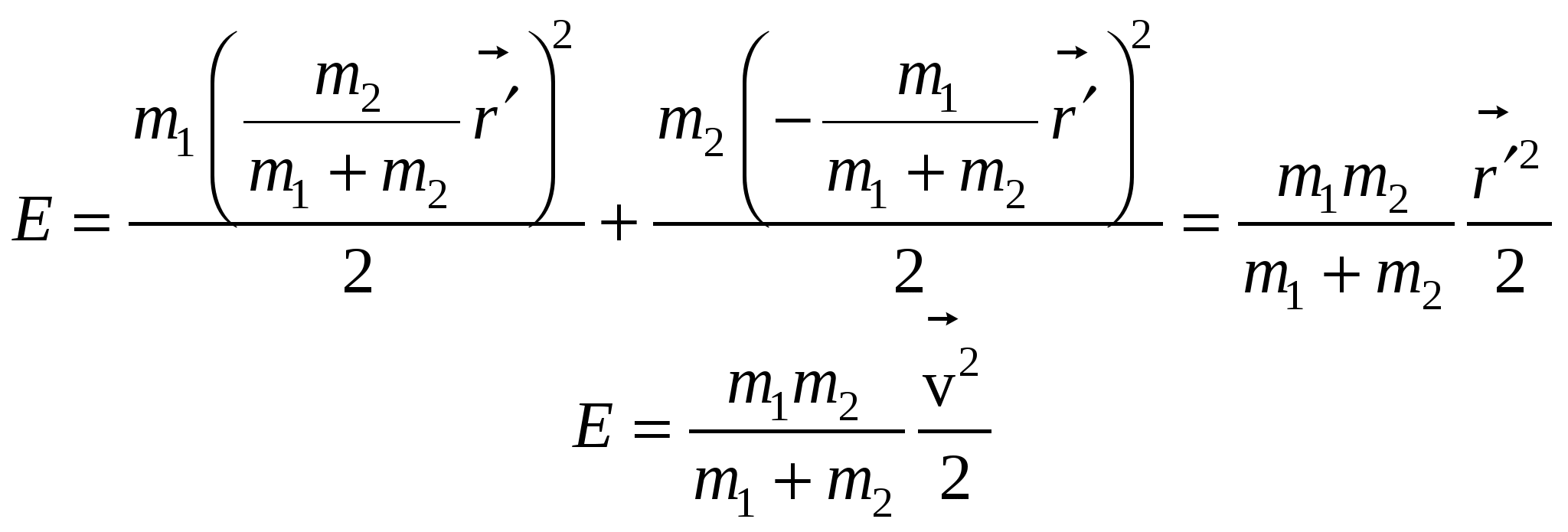



Поскольку по условию вектора скорости шайб перпендикулярны, то

.

Тогда получаем выражение для энергии:

,

где – приведенная масса системы.


1.69. Система состоит из двух шариков с массами m₁ и m₂, которые соединены между собой невесомой пружинкой. В момент времени t = 0шарикам сообщили начальные ско­рости v₁ и v₂, после чего система начала двигаться в поле тяжести Земли. Пренебрегая сопротивлением воздуха, найти зависимость от времени полного импульса этой сис­темы р(t) впроцессе движения и радиуса-вектора r₀(t),характеризующего положение центра инерции относительно его начального положения.

Решение.

Приращение импульса системы равно:

.

Начальный импульс системы равен:

.

Внешняя сила – это сила тяжести:



Тогда получаем: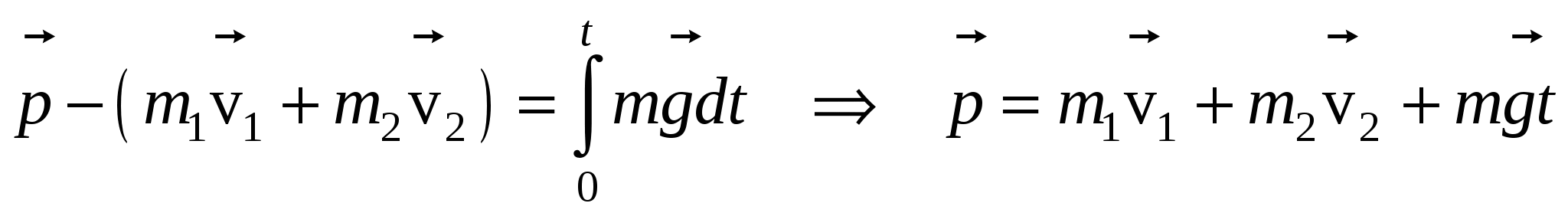

.

Для определения радиуса-вектора r₀(t),характеризующего положение центра инерции относительно его начального положения, проинтегрируем полученное выражение по времени, учтя массу системы :



1.70. Замкнутая металлическая цепочка А массы т = 0,36 кгсоединена нитью с концом вертикальной оси центробежной машины и вращается с постоянной угловой скоростью
= 35 рад/сек.При этом нить составляет угол  = 45⁰ с вертикалью. Пренебрегая массой нити, найти расстояние от центра тяжести цепочки до вертикальной оси, вокруг которой происходит вращение, а также натяжение нити.

Решение.

Н
а цепочку действуют три силы: сила тяжести, сила натяжения нити и центробежная сила.

По 2-му закону Ньютона имеем:

.

Поскольку движение равномерное, то .

В проекции на ось xможно записать:

.

В проекции на ось yможно записать:

Н.

Тогда расстояние от центра тяжести цепочки до вертикальной оси равно: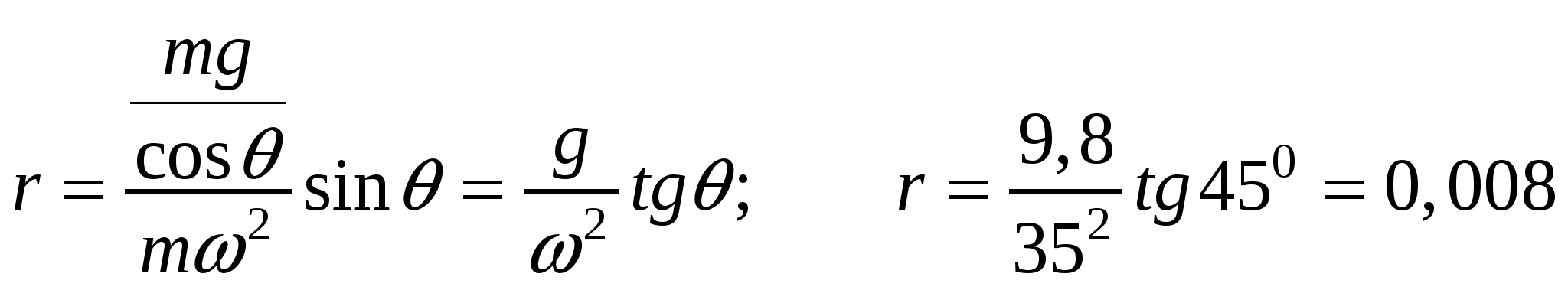

м.
1.71. Круглый конус А, масса которого m = 3,2 кгв угол полураствора =10⁰, катится равномерно без скольжения по круглой конической поверхности В так, что его вершина Оостается неподвижной. Центр тяжести конуса А находится на одном уровне с точкой О, отстоит от нее на расстояние l= 17 см и движется по окружности с постоянной угловой скоростью . Найти:

а) силу трения покоя, действующую на конус А, если = 1,0 рад/сек;

б) при каких значениях движение конуса А будет происходить без скольжения, если коэффициент трения покоя между поверхностями конусов k= 0,25?

Решение.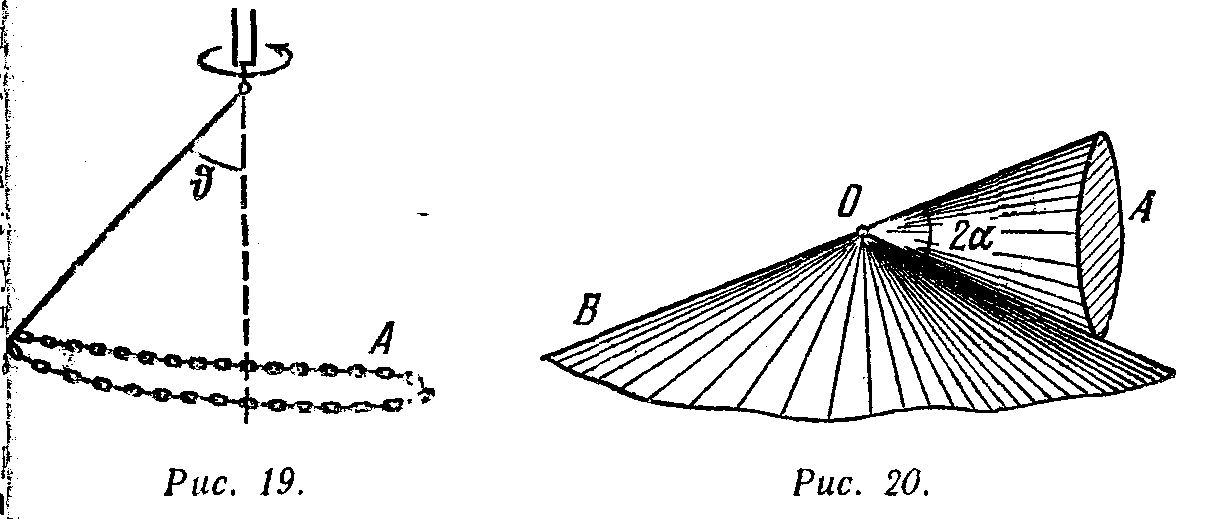



а) Рассмотрим движение центра масс конуса. На него действуют сила тяжести, центробежная сила инерции и сила трения (которая уравновешивает две предыдущие силы). Спроектируем эти силы на ось конуса:

• 
  сила тяжести:
  
• 
  центробежная сила инерции:
  
• 
  сила трения совпадает с осью.
  

Тогда имеем:

Н.

б) Найдем значение , при котором движение конуса А будет происходить без скольжения. В этом случае сила трения .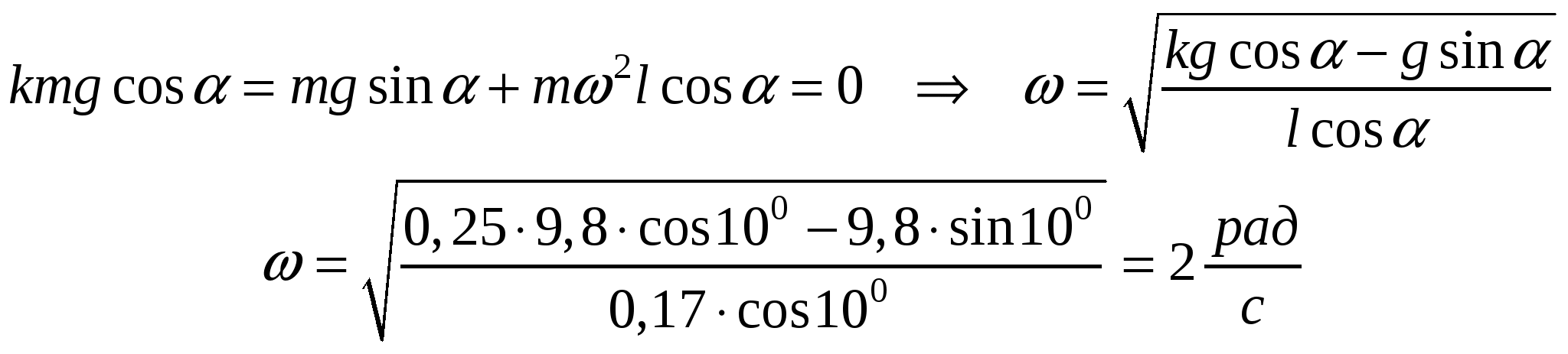



1.72. Плот массы М с находящимся на нем человеком массы m неподвижно стоит в пруду. Относительно плота человек совершает перемещение со скоростью и останавливается. Пренебрегая сопротивлением воды, найти:

а) перемещение плота относительно берега;

б) горизонтальную составляющую силы, с которой человек действует на плот в процессе движения.

Решение.

а) Систему человек-плот можно рассматривать как замкнутую. По закону сохранения импульса, внутренние силы замкнутой системы тел не могут изменить положение их центра масс. Применяя это правило к системе человек-плот, можно считать, что во время перемещения человека по плоту центр масс системы не изменит своего положения, т.е. останется на предыдущем расстоянии от берега.

Пусть центр масс системы человек-плот находится на вертикали, которая проходит в начальный момент через точку С₁, а после перемещения плота – через точку С₂. поскольку эта вертикаль неподвижна относительно берега, то искомое перемещение плота относительно берега можно определить по перемещению центра масс плота О.



Искомое перемещение равно:

.

Суммарный момент сил, действующих на систему относительно горизонтальной оси равен нулю, поэтому для начального положения системы имеем:

.

После перемещения плота имеем:



Подставив полученные значения в формулу для l, получим:

.

Поскольку направления перемещений и , то в векторном виде присутствует знак «-»:



Горизонтальная составляющая силы, с которой человек действует на плот в процессе движения равна:

.
1.74. Цепочка массы m= 1,00 кги длины l= 1,40 мвисит на нити, касаясь поверхности cтола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.

Решение.

Импульс тела, падающего с высоты, которая равна длине цепочке, равен:

,

где v₀ = 0 – начальная скорость; – конечная скорость

Для цепочки имеем:


1.75. Летевшая горизонтально пуля массы т попала, застряв, в тело массы М, которое подвешено на двух одинаковых нитях длины l. В результате нити отклонились влево на угол . Считая т<<М, найти:

а) скорость пули перед попаданием в тело;

б) относительную долю  первоначальной кинетической энергии пули, которая перешла в тепло.

Решение.


а) По закону сохранения импульса имеем:

,

где u – скорость тела и пули после взаимодействия.

Рассмотрим момент отклонения нитей. На центр масс тела действуют силы тяжести и силы натяжения нитей. Имеем в проекции на вертикальную ось:

,

где – отклонение центра масс от начального положения.

В проекции на горизонтальную ось имеем:

.

Тогда получаем:



Тогда получаем:

.
б) относительная доля  первоначальной кинетической энергии пули, которая перешла в тепло равна:



1.77. При взлете ракета выпускает непрерывную струю газа, вылетающую из сопла со скоростью относительно ракеты. Расход газа равен  кг/ceк.Показать, что уравнение движения ракеты имеет вид



где т – масса ракеты в данный момент, – ее ускорение, – внешняя сила (сила тяжести и сила сопротивления воздуха).

Решение.

Пусть в некоторый момент времени t ракета имела массу m и скорость (относительно интересующей нас системы отсчета). Рассмотрим инерциальную систему отсчета, имеющую ту же скорость, что и ракета в данный момент времени. В этой системе отсчета приращение импульса системы «ракета-выброшенная порция газа» за время dtравно:

.

С другой стороны

.

Тогда получаем:

.
1.78. Ракета движется в отсутствие внешних сил, вы­пуская непрерывную струю газа со скоростью , постоянной относительно ракеты. Найти скорость ракеты в момент, когда ее масса равна т, если в начальный момент времени она имела массу т₀и скорость ее была равна нулю. Воспользоваться формулой, приведенной в предыдущей задаче.

Решение.

Уравнение движения ракеты имеет вид:

.

Так как по условию ракета движется в отсутствие внешних сил, то .

Расход топлива равен:



Тогда уравнение движения имеет вид:

.

Интегрируя это уравнение, получим:

.
1.79. Тележка с песком движется по горизонтальной плоскости под действием постоянной силы , совпадающей по направлению с вектором скорости. При этом песок высыпается через отверстие в дне с постоянной скоростью  кг/сек.Найти ускорение и скорость тележки в момент времени t, если в начальный момент t = 0 тележка с песком имела массу m₀ и ее скорость была равна нулю. Трением пренебречь.

Решение.

Пусть в начальный момент времени t тележка имела массу m₀ и скорость (относительно интересующей нас системы отсчета). Рассмотрим инерциальную систему отсчета, имеющую ту же скорость, что и тележка в данный момент времени. В этой системе отсчета приращение импульса системы «тележка-песок» за время dtравно:

.

С другой стороны

.

Тогда получаем:

.

Для определения скорости в момент времени t проинтегрируем полученное выражение:

.
1.80. Платформа А массы т начинает двигаться вправо под действием постоянной силы . Из бунке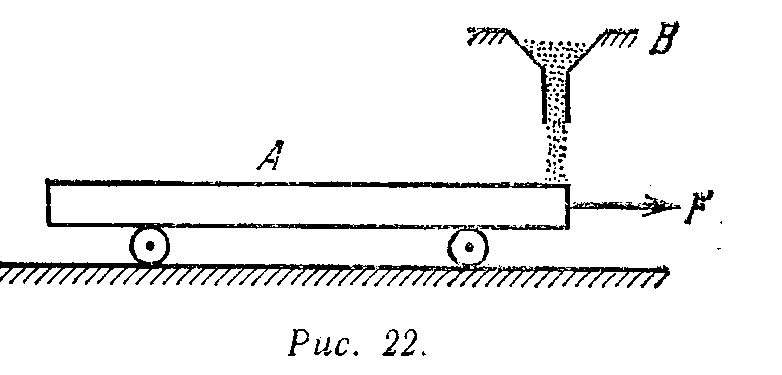ра В на нее высыпается песок. Скорость погрузки постоянна и равна кг/сек.Найти зависимость от времени скорости и ускорения платформы в процессе погрузки. Трением в колесах пренебречь.

Решение.



Пусть в некоторый момент времени t платформа имела массу m + tи скорость (относительно интересующей нас системы отсчета). Рассмотрим инерциальную систему отсчета, имеющую ту же скорость, что и тележка в данный момент времени. В этой системе отсчета приращение импульса системы «тележка-песок» за время dtравно:



С другой стороны

.

Тогда получаем:

.

Для определения зависимости ускорения от времени продифференцируем данное выражение по времени:

.
1.76. Пушка массы М начинает свободно скользить вниз по наклонной плоскости, составляющей угол с горизонтом. Когда пушка прошла путь l, произвели выстрел в горизонтальном направлении, в результате которого снаряд вылетел с импульсом р, а сама пушка остановилась. Пренебрегая массой снаряда по сравнению с массой пушки найти продолжительность выстрела .

Решение.

П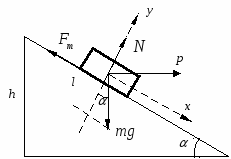риращение импульса системы равно:

.

Проекция силы тяжести на ось x равна:

.

Проекция начального импульса пушки на ось x равна:

.

Проекция конечного импульса пушки на ось x равна:

.

Тогда получаем:


1.73. Через неподвижный блок перекинута веревка, на одном конце которой висит лестница с человеком, а на другом — уравновешивающий груз массы М. Человек, масса которого т, медленно совершил перемещение относительно лестницы вверх и остановился. Пренебрегая массами блока и веревки и трением в блоке, найти перемещение центра инерции этой системы.

Решение.

Искомое перемещение аналогично задаче 1.72 равно:

.

Суммарный момент сил, действующих на систему относительно горизонтальной оси равен нулю, поэтому для начального положения системы имеем:

.

После перемещения плота имеем:



Подставив полученные значения в формулу для l, получим:

.