Матанализ. доки. 1. аддитивность неопределенного интеграла относительно функций (д)
 Скачать 20.27 Kb. Скачать 20.27 Kb.
|
|
1. аддитивность неопределенного интеграла относительно функций (д) 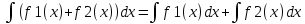 (*) (*)Д – пусть 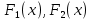 – первообразные функций f1(x), f2(x) соответственно, тогда – первообразные функций f1(x), f2(x) соответственно, тогда 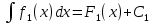 , , 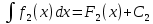 => => 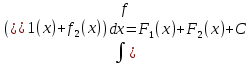 . . 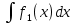 + + 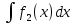 = = 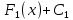 + +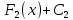 . Т.к С1, С2, С – произвольные константы, то совокупность функций в левой части (*) и в правой совпадают . Т.к С1, С2, С – произвольные константы, то совокупность функций в левой части (*) и в правой совпадают2. Замена переменной в неопределенном интеграле (д); Пусть t=y(x) функция дифференцируемая и определенная на множестве E, область значений этой функции множество D. Пусть функция f(t) имеет на множестве D первообразную F(t). Тогда функция f(y(x)) y’(x) имеет первообразную на множестве E равную F(y(x)), т.е 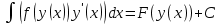 . .Д - Дано 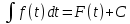 Рассмотрим 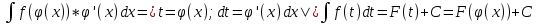 3. Формула интегрирования по частям в неопределенном интеграле (д); Пусть функции u(x) и v(x) дифференцируемы на множестве E, у функции v(x) * u’(x) существует первообразная , тогда у функции u(x) * v’(x) (u(x) * d(v(x))) существует первообразная на множестве E и выполняется равенство: 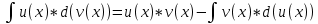 . .Д – Найдем производную (UV)’ = U’V + UV’, тогда U*V’ = (UV)’ – U’V (*) Множество первообразных правой части имеет вид 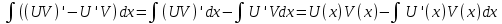 Из (*) следует что 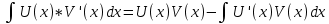 4. Разложение правильной рациональной дроби с действительными корнями знаменателя (д); Пусть 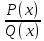 - правильная рациональная дробь. Если число a является вещественным корнем кратности a≥1 многочлена Q(x). Т.е - правильная рациональная дробь. Если число a является вещественным корнем кратности a≥1 многочлена Q(x). Т.е 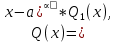 и и 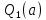 ≠ 0, то существует вещественное число A и многочлен ≠ 0, то существует вещественное число A и многочлен 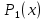 с вещественными коэффициентами, такие что: с вещественными коэффициентами, такие что: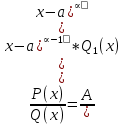 Где дробь Где дробь 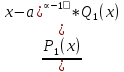 также является правильной также является правильнойД – Для любого вещественного числа А прибавляя и вычитая из дроби 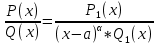 выражение выражение 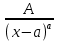 получим получим 5. Необходимое условие интегрируемости функции (д); Если функция f(x) интегрируема на отрезке [a;b], то она ограничена на этом отрезке. Д – ПП – пусть f(x) не ограничена на [a,b]. Тогда при любом разбиении τ отрезка [a,b] найдется частичный отрезок [xi-1, xi] на котором функция f(x) не ограничена. Значит моно на этом отрезке выбрать (.) ξ, так что |f(ξ i)| > M где M > 0 – любое число. Значит слагаемое f(ξ i) * 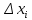 в интегральной сумме I(f, xi, ξ i) можно сделать сколь угодно большим при любом разбиении τ. Поэтому интегральная сумма I(f, xi, ξ i) не может стремиться к конечному пределу. Значит f(x) не интегрируема – получили противоречие => f(x) ограничена на [a,b]# в интегральной сумме I(f, xi, ξ i) можно сделать сколь угодно большим при любом разбиении τ. Поэтому интегральная сумма I(f, xi, ξ i) не может стремиться к конечному пределу. Значит f(x) не интегрируема – получили противоречие => f(x) ограничена на [a,b]#6. Свойства верхних и нижних интегральных сумм: 7. Необходимое и достаточное условие интегрируемости функции на отрезке (д); . Необходимое и достаточное условие интегрируемости функции - Для того чтобы ограниченная на отрезке [a,b] функция f(x) была интегрируема на [a,b] ⇔ чтобы для ∀ε > 0 нашлось такое разбиение ፖ отрезка [a,b], что S-s ≤ ε. 8. Теорема кантора, следствие (д); Теорема Кантора - Если f(x) непрерывна на [a,b], то она равномерно непрерывна на [a,b]. Следствие: Пусть функция f(x) непрерывна на отрезке [a,b]. Тогда ∀ε > 0 ∃δ = δ(ε) > 0 такое, что на каждом частичном отрезке [  ] лежащем в отрезке [a,b] длина которого ∆ ] лежащем в отрезке [a,b] длина которого ∆ < δ выполняется < δ выполняется  < ε. < ε.Д – Пусть E > 0. Из теоремы Кантора т.к f(x) непрерывна на [a,b] => f(x) равномерно непрерывна на каждом [a,b] =>  Выберем произвольный отрезок [xi-1, xi] : 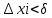 Тогда для 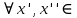 [xi-1, xi] => [xi-1, xi] => 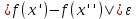 Т.к f(x) непрерывна на [a,b] => f(x) непрерывна на [xi-1, xi]. По второй теореме Вейештраса 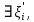  для для  [xi-1, xi]. Т.е mi = f( [xi-1, xi]. Т.е mi = f( , Mi = f( , Mi = f(  . Поскольку . Поскольку 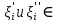 [xi-1, xi] и [xi-1, xi] и 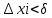 => | => | 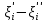 | |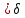 . . Тогда 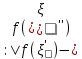 | = Mi – mi = wi < ε | = Mi – mi = wi < ε9/ Интегрируемость непрерывной функции (д); Если функция f(x) непрерывна на [a,b], то она интегрируема на этом отрезке. Д – f(x) – непрерывна на [a,b] |
