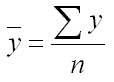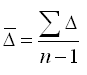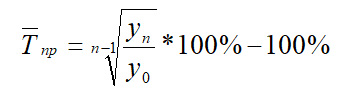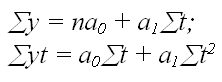вариант 8. Статистика . таможенное дело.. Вариант8_статистика. 1. Анализ рядов динамики 5 Статистические показатели денежного обращения 8
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Результаты группировки представим в таблице 3. Таблица 3 – Группировка предприятий по рыночной стоимости предприятия
Для получения результатов структурной группировки необходимо абсолютные показатели заменить относительными показателями структуры (табл. 4). Таблица 4 – Результаты структурной группировки предприятий по рыночной стоимости предприятия
По результатам структурной группировки можно сделать вывод о том, что большая часть предприятий имеет среднюю рыночную стоимость; с увеличением рыночной стоимости повышается число предприятий, имеющих более высокую рыночную стоимость. Пропорционально рыночной стоимости увеличиваются и другие показатели: выручка от реализации; чистая прибыль; выплаченные дивиденды; себестоимости сырья, материалов; валовая прибыль. 4) Для проведения аналитической группировки в качестве результативного признака выберем рыночную стоимость предприятия, а в качестве факторного – сумму выплаченных дивидендов. Для выполнения группировки разделим предприятия на пять групп по сумме выплаченных дивидендов с равными интервалами (табл. 5). Таблица 5 – Группировка предприятий по сумме выплаченных дивидендов
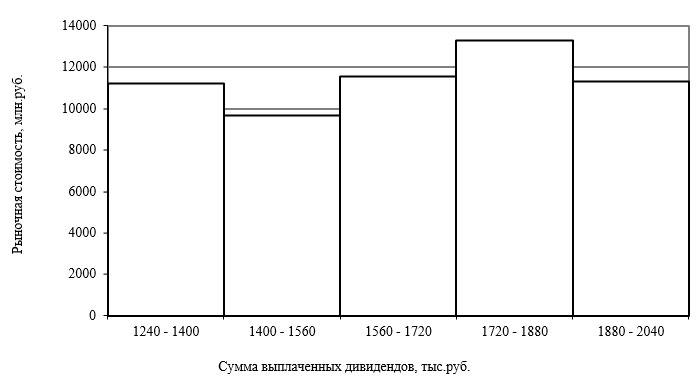
По данным таблицы 5 построим гистограмму распределения рыночной стоимости предприятий от суммы выплаченных дивидендов (рис. 1).
Рисунок 1 – Гистограмма распределения рыночной стоимости по выплаченным дивидендам, млн. руб. Следовательно, можно сделать вывод о наличии прямой зависимости рыночной стоимости и суммы выплаченных дивидендов – чем больше предприятия тратят на выплату дивидендов, тем выше их рыночная стоимость. 5) Для сгруппированного факторного признака «сумма выплаченных дивидендов» проведем эмпирическое исследование с помощью определения частотных характеристик ряда распределения и графического представления результатов расчетов. На основе частоты ni рассчитаем частость: а также накопленные частоты и частости. (табл. 6). Таблица 6 – Расчет частотных характеристик предприятий по суме выплаченных дивидендов
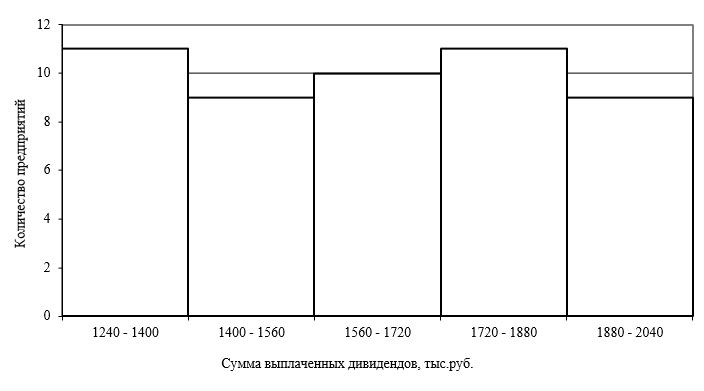
По данным таблицы построим гистограмму, полигон частот и кумуляту распределения предприятий по сумме выплаченных дивидендов (рис. 2, 3, 4).
Рисунок 2 – Гистограмма распределения количества предприятий по сумме выплаченных дивидендов
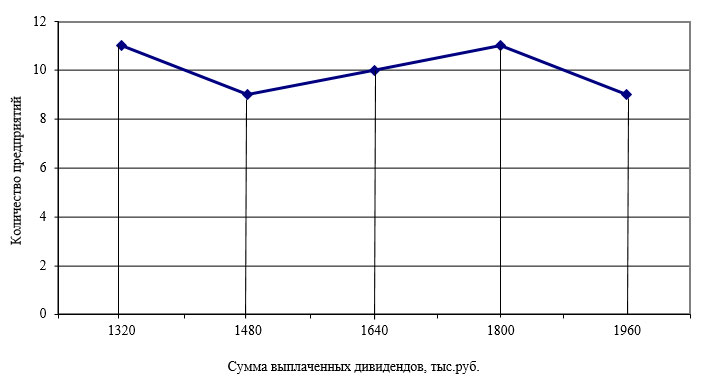
Рисунок 3 – Полигон частот распределения предприятий по сумме выплаченных дивидендов
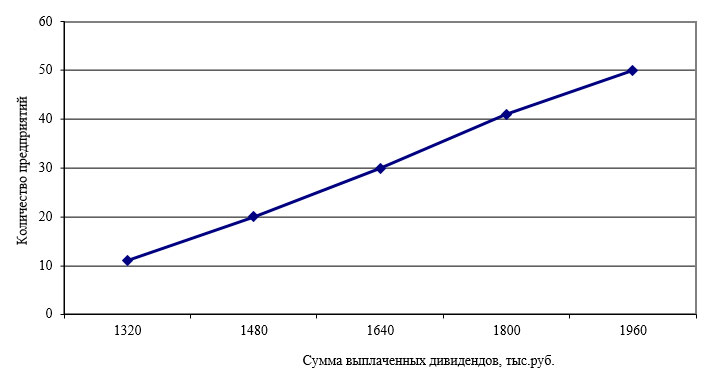
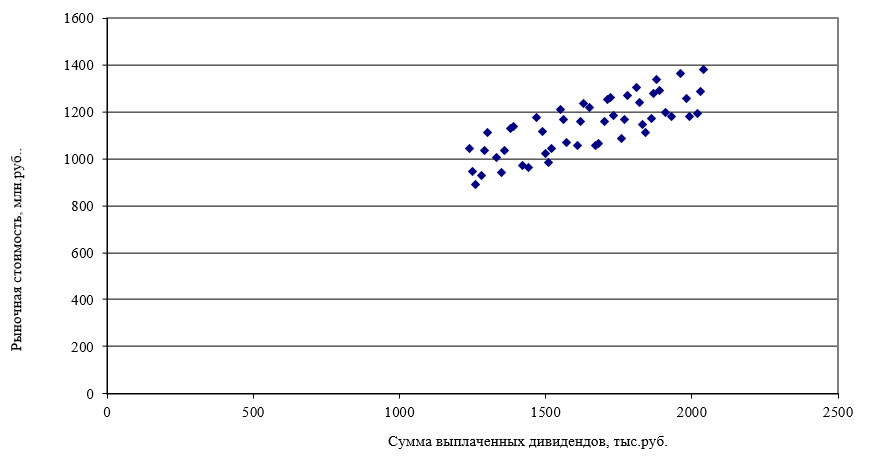
Рисунок 4 – Кумулята распределения предприятий по сумме выплаченных дивидендов 6) Для выявления взаимосвязи между рыночной стоимостью и суммой выплаченных дивидендов построим эмпирический график зависимости (рис. 5).
Рисунок 5 – Эмпирическая зависимость рыночной стоимости от суммы выплаченных дивидендов Предположительно имеется линейная зависимость между изучаемыми результативным и факторным признаками. Уравнение линии регрессии в данном случае будет выглядеть следующим образом: y=a+bx, где y – теоретическое значение результативного признака; x – факторный признак; a и b – значения коэффициентов регрессии. Для расчетов построим вспомогательную таблицу 7. Таблица 7 – Исходные и расчетные данные для определения коэффициентов уравнения регрессии
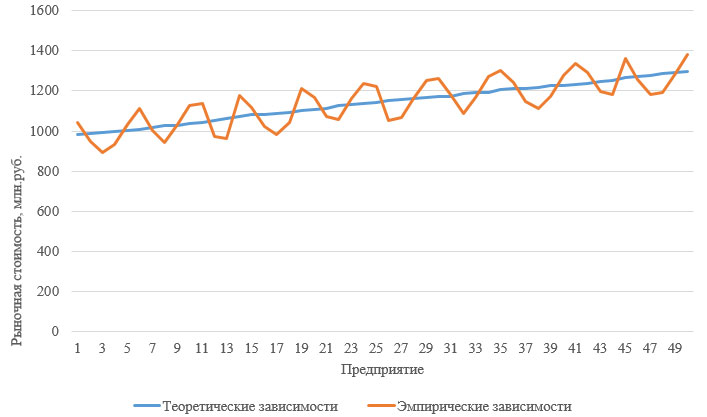
Следовательно: b = 0,392 a = 496,504 Уравнение регрессии будет выглядеть следующим образом: y = 496,504+0,392x Для количественной оценки тесноты связи определим значение парного коэффициента корреляции: r = 0.7805. Данное значение коэффициента корреляции положительное и близкое к единице свидетельствует о наличии прямой линейной взаимозависимости между анализируемыми показателями. Построим график теоретических зависимостей:
Рисунок 6 – Теоретические и эмпирические зависимости рыночной стоимости от суммы выплаченных дивидендов 7. Рассчитаем цепные абсолютные приросты по формуле: Δц = yi - yi-1 Δц1 = 1410.7 - 1256.9 = 153.80 млрд. руб. Δц2 = 1667 - 1410.7 = 256.30 млрд. руб. Δц3 = 1745.7 - 1667 = 78.70 млрд. руб. Δц4 = 1882.3 - 1745.7 = 136.60 млрд. руб. Рассчитаем базисные абсолютные приросты по формуле: Δб = yi - y1 Δб1 = 1410.7 - 1256.9 = 153.80 млрд. руб. Δб2 = 1667 - 1256.9 = 410.10 млрд. руб. Δб3 = 1745.7 - 1256.9 = 488.80 млрд. руб. Δб4 = 1882.3 - 1256.9 = 625.40 млрд. руб. Рассчитаем цепные коэффициенты роста по формуле: Кр.ц = yi : yi-1 Кр.ц1 = 1410.7 / 1256.9 = 1.122 Кр.ц2 = 1667 / 1410.7 = 1.182 Кр.ц3 = 1745.7 / 1667 = 1.047 Кр.ц4 = 1882.3 / 1745.7 = 1.078 Рассчитаем базисные коэффициенты роста по формуле: Кр.б = yi : y1 Кр.б1 = 1410.7 / 1256.9 = 1.122 Кр.б2 = 1667 / 1256.9 = 1.326 Кр.б3 = 1745.7 / 1256.9 = 1.389 Кр.б4 = 1882.3 / 1256.9 = 1.498 Рассчитаем цепные темпы роста по формуле: Тр.ц = yi : yi-1 * 100% Тр.ц1 = 1410.7 / 1256.9 * 100% = 112.24% Тр.ц2 = 1667 / 1410.7 * 100% = 118.17% Тр.ц3 = 1745.7 / 1667 * 100% = 104.72% Тр.ц4 = 1882.3 / 1745.7 * 100% = 107.82% Рассчитаем базисные темпы роста по формуле: Тр.б = yi : y1 * 100% Тр.б1 = 1410.7 / 1256.9 * 100% = 112.24% Тр.б2 = 1667 / 1256.9 * 100% = 132.63% Тр.б3 = 1745.7 / 1256.9 * 100% = 138.89% Тр.б4 = 1882.3 / 1256.9 * 100% = 149.76% Рассчитаем цепные темпы прироста по формуле: Тпр.ц = Δц : yi-1 * 100% Тпр.ц1 = 153.80 / 1256.9 * 100% = 12.24% Тпр.ц2 = 256.30 / 1410.7 * 100% = 18.17% Тпр.ц3 = 78.70 / 1667 * 100% = 4.72% Тпр.ц4 = 136.60 / 1745.7 * 100% = 7.82% Рассчитаем базисные темпы прироста по формуле: Тпр.б = Δб : y1 * 100% Тпр.ц1 = 153.80 / 1256.9 * 100% = 12.24% Тпр.ц2 = 410.10 / 1256.9 * 100% = 32.63% Тпр.ц3 = 488.80 / 1256.9 * 100% = 38.89% Тпр.ц4 = 625.40 / 1256.9 * 100% = 49.76% Рассчитаем показатель асолютного значения 1% прироста по формуле: |%| = 0,01 * yi-1 Тпр.ц1 = 0.01 * 1256.9 = 12.57 млрд. руб. Тпр.ц2 = 0.01 * 1410.7 = 14.11 млрд. руб. Тпр.ц3 = 0.01 * 1667 = 16.67 млрд. руб. Тпр.ц4 = 0.01 * 1745.7 = 17.46 млрд. руб. Полученные расчеты сведем в таблицу Таблица 8 – Динамика валового регионального продукта по Красноярскому краю.
Далее определим средние показатели ряда динамики. Средний уровень ряда определим по формуле:
Средний абсолютный прирост определим по формуле:
Рассчитаем средний темп роста по формуле: 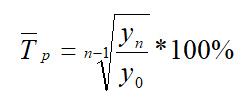 Tр.средн. = (5-1)√(1882.3 / 1256.9) = 110.62% Средний темп прироста определим по формуле:
Анализ полученных результатов показывает, что за 2013 – 2017 гг валовой региональный продукт по Красноярскому краю увеличился на 625.40 млрд. руб. или на 49.76%. Среднегодовая величина валового регионального продукта по Красноярскому краю составила 1592.52 млрд. руб. При этом в среднем ежегодно объем ВРП по Красноярскому краю увеличивался на 156.35 млрд. руб. или на 10.62%. Значение 1% прироста увеличилось с 12.57 до 17.46 млрд. руб. Далее построим уравнение тренда. Для этого построим вспомогательную таблицу: Таблица 9 – Вспомогательные расчеты параметров уравнения линейного тренда
Система нормальных уравнений будет иметь вид:
Для определения параметров уравнения подставим в приведенную систему исходные данные и получим: 7962,6 = 5а0+15а1 25473,6 = 15а0+55а1 Выравняем коэффициенты при а0, разделив первое уравнение на 5, а второе на 15 и получим: 1592,52=1а0+3а1 1698,24=1а0+3,67а1 Вычтем из второго уравнения первое и определим значение а1: а1 = 157,79 Подставим полученное значение а1 в одно из уравнений и определим значение а0: а0 = 1119,15 Тогда уравнение будет иметь вид: y = 1119,15+157,79*t R2 = 0,9721 R = 0,986 – связь очень тесная. Полученное уравнение показывает, что в среднем объем ВРП по Красноярскому краю закономерно возрастает ежегодно на 157,79 млрд. руб., начиная с выравненного исходного уровня 1119,15 млрд. руб. Список используемой литературыБалдин, К.В. Общая теория статистики. Учебное пособие / К.В. Балдин. – М.: Дашков и Ко, 2017. - 312 с. Батракова, Л.Г. Социально-экономическая статистика / Л.Г. Батракова. – М.: Логос, 2015. - 480 с. Батракова, Л.Г. Теория статистики / Л.Г. Батракова. – М.: КноРус, 2015. - 528 с. Елисеева, И.И. Статистика (+ CD) / И.И. Елисеева. – М.: Питер, 2015. - 368 с. Ефимова, М.Р. Социальная статистика / М.Р. Ефимова. – М.: Финансы и статистика, 2016. - 560 с. Ефимова, М.Р. Социально-экономическая статистика / М.Р. Ефимова, А.С. Аброскин. – М.: Юрайт, 2016. - 592 с. Захаренков, С.Н. Статистика / С.Н. Захаренков. – М.: Современная школа, 2015. - 272 с. Илышев, А.М. Общая теория статистики / А.М. Илышев. – М.: КноРус, 2015. - 432 с. Ковалев, В.В. Теория статистики / В.В. Ковалев. – М.: Юрайт, 2015. - 464 с. 1 Илышев, А.М. Общая теория статистики / А.М. Илышев. – М.: КноРус, 2015. – С. 228. 2 Балдин, К.В. Общая теория статистики. Учебное пособие / К.В. Балдин. – М.: Дашков и Ко, 2017. – С. 187. 3 Ефимова, М.Р. Социально-экономическая статистика / М.Р. Ефимова, А.С. Аброскин. – М.: Юрайт, 2016. – С. 318. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||