1 билет функция F(x) называется первообразной для f(x) в интервале (а,в), если F(x) определена в интервале (а,в) и ее производная равна f(x). F(x)f(x) Теорема о разности первообразных
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
1 БИЛЕТ Функция F(x) называется первообразной для f(x) в интервале (а,в), если F(x) определена в интервале (а,в) и ее производная равна f(x). F’(x)=f(x) Теорема о разности первообразных. Пусть F1(x) и F2(x) — две первообразные для функции f(x) на некотором промежутке X, тогда для любого x из этого промежутка F2(x)=F1(x) + C или F2(x) – F1(x) = C, где C — произвольная постоянная 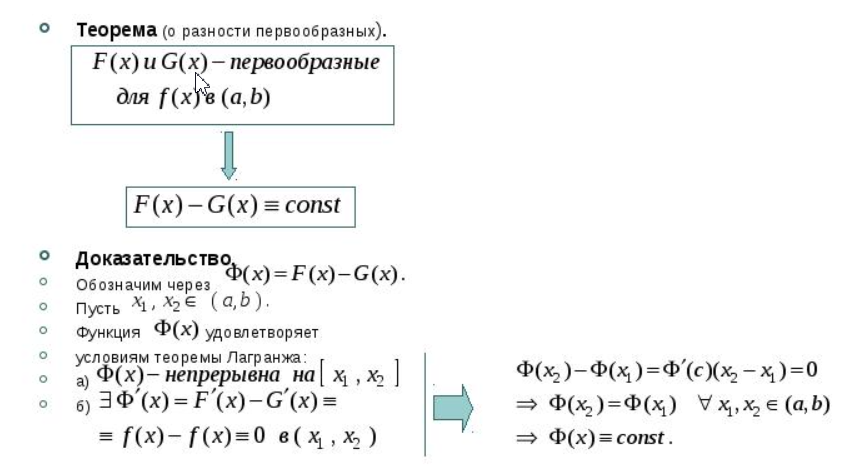 Неопределенным интегралом от функции f (x) называется совокупность всех первообразных этой функции, то есть выражение ∫ f ( x ) d x = F ( x ) + C Свойства неопределённого интеграла1.1. Производная неопределенного интеграла равна подынтегральной функции: (∫ f(x)dx)′ = f(x). 1.2. Дифференциал от неопределенного интеграла равен подынтегральному выражению: d(∫ f(x)dx) = f(x)dx. 1.3. Неопределенный интеграл от производной функции равен сумме этой функции и произвольной постоянной: ∫ f′(x)dx = f(x) + C, C — const. 1.4. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: ∫ df(x) = f(x) + C, C — const. ЛИНЕЙНОСТЬ Свойство 2. Неопределенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме неопределенных интегралов от слагаемых функций: ∫ (f(x) ± g(x))dx = ∫ f(x)dx ± ∫ g(x)dx Свойство. 2.1 Постоянный множитель можно выносить за знак неопределенного интеграла: ∫ k f(x)dx = k∫ f(x)dx, k — const, k ≠ 0и Доказательство суммы и разности 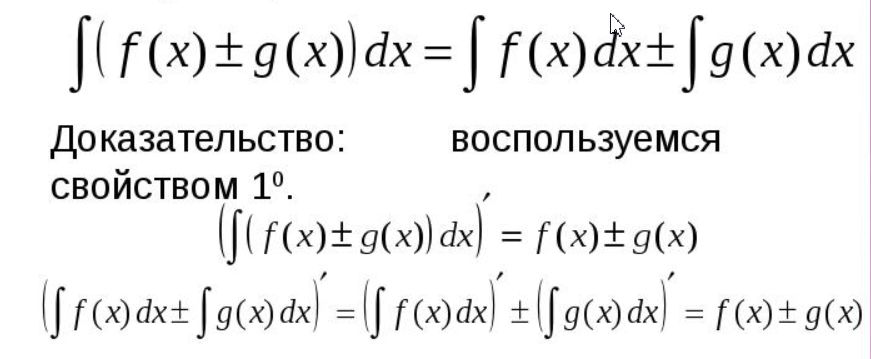 2 билет 1  2   |
