практика 1 тидз. шенон пр1. 1. Биография 1 Детство и юность

• Название: 1. Биография 1 Детство и юность
• Анкор: практика 1 тидз
• Дата: 16.01.2023
• Размер: 38.32 Kb.
• Имя файла: шенон пр1.docx
• Тип: Биография; #889478

Цель работы

Изучить трансмиссионную модель массовых коммуникаций на примере статистической теории связи («количественной теории связи») К. Шеннона.

1. Биография

1.1 Детство и юность.

Клод Шэннон родился 30 апреля 1916 года в городе Петоцки, штат Мичиган, США. Первые шестнадцать лет своей жизни Клод провел в Гэйлорде, Мичиган, где в 1932 году Шеннон закончил обычную общую школу. В юности он работал курьером .Его отец был адвокатом, а мать была преподавателем иностранных языков и впоследствии стала директором средней школы в Гэйлорде. Молодой Шеннон увлекался конструированием механических и автоматических устройств. Он собирал модели самолетов и радиотехнические цепи, создал радиоуправляемую лодку и телеграфную систему между домом друга и своим домом. Временами ему приходилось исправлять радиостанции для местного универмага.

Известно, что Шеннон являлся дальним родственником Томаса Эдисона.

1.2 Университетские годы

В 1932 году Шеннон поступил в «Мичиганский университет». В 1936 году Клод окончил университет, получив степень бакалавра по специальностям: математик и электротехник.

После окончания университете, Шеннон устроился в Массачусетский технологический институт (MIT), там он работал работал ассистентом-исследователем. 

Ему приходилось выполнять обязанности оператора на механическом вычислительном устройстве, аналоговом компьютере, называемом «дифференциальный анализатор», который разработал его научный руководитель Вэниваром Бушем. Изучая сложные, узкоспециализированные электросхемы дифференциального анализатора, Шеннон увидел, что концепции Буля могут получить достойное применение. 

В 1940 году была завершена его докторская диссертация «Алгебра теоретической генетики».

Шеннон получает докторскую степень по математике и степень магистра по электротехнике.

Шеннон также был заинтересован в применении математики в информационных системах, таких как системы связи. После очередного лета, проведённого в Bell Labs, в 1940 году Шеннон на один академический год стал научным сотрудником в Институте перспективных исследований в Принстоне, штат Нью-Джерси, США.

1.3 Военное время

С началом Второй мировой войны Т. Фрай возглавил работу над программой для систем управления огнем для противовоздушной обороны. Шеннон присоединился к группе Фрая и работал над устройствами, засекавшими самолеты противника и нацеливавшими зенитные установки, также он разрабатывал криптографические системы, в том числе и правительственную связь, которая обеспечивала переговоры Черчилля и Рузвельта через океан. Как говорил сам Шеннон, работа в области криптографии подтолкнула его к созданию теории информации.

1.4 Послевоенное время

В 1948 году обещанный меморандум появился как статья «Математическая теория связи» в двух частях, соответственно, в июле и октябре в Bell System Technical Journal. Эта работа посвящена проблеме кодирования передаваемой информации. В этой фундаментальной работе Шеннон использовал инструменты теории вероятностей, разработанные Норбертом Винером, которые находились в зарождающейся стадии относительно их применения к теории связи в то время. Также Шеннон ввёл важное определение информационной энтропии как меры неопределённости информации в сообщениях. Эта статья по сути положила начало такой науке, как теория информации.

С 1950 по 1956 Шеннон занимался созданием логических машин, таким образом, продолжая начинания фон Неймана и Тьюринга. Он создал машину, которая могла играть в шахматы, задолго до создания Deep Blue. В 1952 Шеннон создал обучаемую машину поиска выхода из лабиринта.

В 1956 году Шеннон покидает «BELL LABS», но продолжат их консультировать. Он также продолжает работу в MIT до 1978 года.

1.5 Последние годы жизни

У Шеннона развилась болезнь Альцгеймера, и последние несколько лет своей жизни он провёл в доме престарелых в штате Массачусетс. Клод Шеннон ушёл из жизни 24 февраля 2001 года.

2. Первые научные исследования

Статья «Символический анализ релейных и переключательных схем».

После того, как он проработал лето 1937 года в Bell Telephone Laboratories, он написал основанную на своей магистерской работе того же года статью «Символический анализ релейных и переключательных схем». 

В этой работе он показал, что переключающиеся схемы могут быть использованы для замены схем с электромеханическими реле, которые использовались тогда для маршрутизации телефонных вызовов. Затем он расширил эту концепцию, показав, что эти схемы могут решить все проблемы, которые позволяет решить Булева алгебра. 

За эту статью Шеннон был награждён Премией имени Альфреда Нобеля Американского института инженеров-электриков в 1940 году. Говард Гарднер из Гарвардского университета отозвался о работе Шеннона, как о «возможно, самой важной, а также самой известной магистерской работе столетия».

3. Математическая теория связи

Статья «Математическая теория связи» была опубликована в 1948 году и сделала Клода Шеннона всемирно известным. В ней Шеннон изложил свои идеи, ставшие впоследствии основой современных теорий и техник обработки, передачи и хранения информации. Перед написанием статьи Шеннон ознакомился с работами Хартли и Найквиста. В статье Шеннон обобщил их идеи, ввёл понятие информации, содержащейся в передаваемых сообщениях. В качестве меры информации передаваемого сообщения M Хартли и Найквист предлагали использовать логарифмическую функцию I = log (M).

Шеннон разделил системы связи на несколько частей следующим образом:

• 
  Источник информации
  
• 
  Передатчик
  
• 
  Канал
  
• 
  Приёмник
  
• 
  Пункт назначения
  

Шеннон группировал системы связи в три категории: дискретные, непрерывные и смешанные, причём утверждая, что дискретный случай основа остальных двух, но имеет большее применение.

Шеннон первым начал рассматривать передаваемые сообщения и шумы в каналах связи с точки зрения статистики, рассматривая как конечные, так и непрерывные множества сообщений. Шеннон стал рассматривать источник сообщений как множество всех возможных сообщений, а канал как множество всевозможных шумов.

Созданная им теория информации дает ключ к решению двух основных проблем теории связи:

• 
  устранение избыточности источника сообщений
  
• 
  кодирование сообщений, передаваемых по каналу связи с шумами.
  

Первая теорема в его статье описывает связь по зашумлённому каналу следующим образом:

Пусть источник сообщений имеет энтропию H (бит на символ), а C - пропускная способность канала (бит в секунду). Тогда возможно такое кодирование информации, при котором средняя скорость передачи через данный канал будет равняться C/H-e (epsilon) символов в секунду, где e (epsilon) — сколь угодно малая величина. Дополнительно, средняя скорость передачи данных не может быть больше C/H.

Главная идея этой теоремы состоит в том, что количество информации, которое возможно передать, зависит от энтропии или, другими словами, случайности сообщений источника. Следовательно, основываясь на статистической характеристике источника сообщений, возможно кодировать информацию так, чтобы достичь максимальную скорость, которую позволяет достичь канал, то есть желаемую пропускную способность канала. Это было революционное утверждение, так как инженеры ранее полагали, что максимум информации исходного сигнала, которое можно передать через среду, зависит от таких факторов, как, например, частота, но никак не свойства сигнала.

Вторая теорема Шеннона описывает связь в зашумлённом канале. Шеннон утверждает:

Пусть источник сообщений имеет энтропию H на одну секунду, а C - пропускная способность канала. Если H <= C, то возможно такое кодирование информации, при котором данные источника будут переданы через канал со сколь угодно малым количеством ошибок. Если H>C, то возможно кодирование, при котором неоднозначность полученной информации будет меньше, чем H-C+e (epsilon), где e - сколь угодно малая величина. Дополнительно, не существует методов кодирования, которые дадут неоднозначность меньше чем H-C.

Идея, которую высказал Шеннон, заключается в том, что не важно, как "шумит" канал, всё равно существует способ кодирования, позволяющий безошибочно передать информацию через канал (пока выполняется H). И эта идея является революционной, поскольку люди до этого считали, что существует какой-то порог значения шума в канале, что передача желаемой информации становится невозможна.

Он вывел формулу для скорости передачи информации источником сообщений R и для пропускной способности канала C, размерность каждой скорости - бит в секунду. Как следствие из предыдущей теоремы верно следующее утверждение:

Пусть R - скорость передачи информации источником сообщений, а C - пропускная способность канала. Тогда R, и что возможно такое кодирование информации, при котором количество ошибочных бит в единицу времени будет меньше любой заранее выбранной положительной константы e(epsilon) . В его доказательстве фигурирует множество всевозможных кодирований сообщений источника в потоки бит, и он показал, что случайно выбранное из этого множества кодирование будет обладать желаемым указанным выше свойством с высокой вероятностью.

Другими словами: любой канал с шумом характеризуется максимальной скоростью передачи информации, этот предел назван в честь Шеннона. При передаче информации со скоростями, превышающими этот предел, происходят неизбежные искажения данных, но снизу к этому пределу можно приближаться с необходимой точностью, обеспечивая сколь угодно малую вероятность ошибки передачи информации в зашумлённом канале.

Развитая Шенноном теория информации помогла решить главные проблемы, связанные с передачей сообщений, а именно: устранить избыточность передаваемых сообщений, произвести кодирование и передачу сообщений по каналам связи с шумами. Решение проблемы избыточности подлежащего передаче сообщения позволяет максимально эффективно использовать канал связи. К примеру, современные повсеместно используемые методы снижения избыточности в системах телевизионного вещания на сегодняшний день позволяют передавать до шести цифровых программ телевидения в полосе частот, которую занимает обычный сигнал аналогового телевидения.

Решение проблемы передачи сообщения по каналам связи с шумами при заданном соотношении мощности полезного сигнала к мощности сигнала помехи в месте приёма позволяет передавать по каналу связи сообщения со сколь угодно малой вероятностью ошибочной передачи. Также, это отношение определяет пропускную способность канала. Это обеспечивается применением кодов, устойчивых к помехам, при этом скорость передачи сообщений по данному каналу должна быть ниже его пропускной способности.

В своих работах Шеннон доказал принципиальную возможность решения обозначенных проблем, это явилось в конце 1940-х годов настоящей сенсацией в научных кругах.

4. Основные положения. Теоремы Шеннона

1. 
   Теоремы Шеннона для источника общего вида
   

• 
  описывают возможности кодирования источника общего вида с помощью разделимых кодов. Другими словами, описываются максимально достижимые возможности кодирования без потерь.
  

Прямая теорема

В применении к побуквенному кодированию прямая теорема может быть сформулирована следующим образом:

Существует префиксный, то есть разделимый код, для которого средняя длина сообщений отличается от нормированной энтропии не более, чем на единицу:



где:

1. 
   U - некоторый источник сообщений, а также множество всех его сообщений
   
2. 
   w1,w2,...,wK - длины сообщений источника после кодирования
   
3. 
   - средняя длина сообщений
   
4. 
   H (U) - энтропия источника
   
5. 
   D - количество букв в алфавите кодирования (например, 2 для двоичного алфавита, 33 — для кодирования заглавными русскими буквами и т. д.)
   

В качестве доказательства теоремы исследуются характеристики кода Шеннона-Фано. Данный код удовлетворяет условиям теоремы, и он обладает указанными свойствами.

Обратная теорема

Ограничивает максимальную степень сжатия, достигаемую с помощью кодирования без потерь. В применении к побуквенному кодированию, описывает ограничение на среднюю длину кодового слова для любого разделимого кода.

Для любого разделимого кода с длинами w1,w2,...,wk средняя длина сообщений больше или равна энтропии источника U, нормированный на двоичный логарифм от числа букв D в алфавите кодера:

2. 
   Теоремы Шеннона для канала с шумами (теоремы Шеннона для передачи по каналу с шумами)
   

• 
  связывают пропускную способность канала передачи информации и существование кода, который возможно использовать для передачи информации по каналу с ошибкой, стремящейся к нулю (при увеличении длины блока)
  

Прямая теорема

Если скорость передачи сообщений меньше пропускной способности канала связи, то существуют коды и методы декодирования такие, что средняя и максимальная вероятности ошибки декодирования стремятся к нулю, когда длина блока стремится к бесконечности.

Обратная теорема

Если скорость передачи больше пропускной способности, то есть , то не существует таких способов передачи, при которых вероятность ошибки стремится к нулю при увеличении длины передаваемого блока.

3. 
   Теоремы Шеннона для источника без памяти
   

• 
  связывают энтропию источника и возможность сжатия кодированием с потерями и последующим неоднозначным декодированием.
  

Прямая теорема показывает, что с помощью кодирования с потерями возможно достичь степени сжатия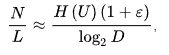



сколь угодно близкой к энтропии источника, но всё же больше последней. Обратная показывает, что лучший результат не достижим.

4. 
   Теорема Шеннона об источнике шифрования (или теорема бесшумного шифрования)
   

• 
  В теории информации теорема Шеннона об источнике шифрования (или теорема бесшумного шифрования) устанавливает предел максимального сжатия данных и числовое значение энтропии Шеннона.
  

Теорема показывает, что (когда в потоке независимо и одинаково распределённых (НОР) случайных переменных количество данных стремится к бесконечности) невозможно сжать данные настолько, что оценка кода (среднее число бит на символ) меньше, чем энтропия Шеннона исходных данных, без потери точности информации. Тем не менее, можно получить код, близкий к энтропии Шеннона без значительных потерь.

Теорема об источнике шифрования для кодов символов приводит верхнюю и нижнюю границу к минимально возможной длине зашифрованных слов как функция энтропии от входного слова (которое представлено как случайная переменная) и от размера требуемой азбуки.

5. 
   Теорема Котельникова (теорема Найквиста — Шеннона, теорема отсчётов)
   

• 
  фундаментальное утверждение в области цифровой обработки сигналов, связывающее непрерывные и дискретные сигналы и гласящее, что «любую функцию F(t), состоящую из частот от 0 до f_1, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом менее чем через 1/(2f_1) секунд».
  

При доказательстве теоремы взяты ограничения на спектр частот 0< ω < ω1, где ω=2πf.

Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временной характеристике точек разрыва. Если сигнал имеет разрывы любого рода в функции зависимости его от времени, то его спектральная мощность нигде не обращается в ноль. Именно это подразумевает понятие «спектр, ограниченный сверху конечной частотой f_c».

Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и обычно имеют разрывы во временно́й характеристике. Соответственно, ширина их спектра бесконечна. В таком случае полное восстановление сигнала невозможно, и из теоремы Котельникова вытекают следствия:

любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой f>2f_c, где f_c — максимальная частота, которая ограничена спектром реального сигнала;

если максимальная частота в сигнале равна или превышает половину частоты дискретизации (наложение спектра), то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.

Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал x(t) можно представить в виде интерполяционного ряда: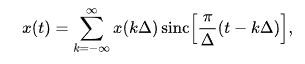