Курсовая работа - Расчет системы передачи дискретных сообщений. Курсовая работа по тэс расчет системы передачи дискретных сообщений Вариант ст гр. Мкс311 Котов Д

• Название: Курсовая работа по тэс расчет системы передачи дискретных сообщений Вариант ст гр. Мкс311 Котов Д
• Дата: 28.01.2022
• Размер: 1.09 Mb.
• Имя файла: Курсовая работа - Расчет системы передачи дискретных сообщений .doc
• Тип: Курсовая; #344661
• страница: 1 из 3

Министерство Образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра Телекоммуникационных Систем

Курсовая работа по ТЭС

Расчет системы передачи дискретных сообщений
Вариант 9.


Выполнил: ст. гр. МКС-311 Котов Д.

Проверил: Комиссаров А.М.

Уфа 2004 г.

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ по курсу

"ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ"
Рассчитать основные характеристики системы передачи сообщений (рис.1), включающий в себя источник сообщений (ИС), дискретизатор (Д), кодирующее устройство (Кодер), модулятор (Мод), линия связи, демодулятор (Дем), декодер (Дек) и фильтр-восстановитель (ФВ).

ИС

Д

Кодер

Мод

Линия связи

Дем

Дек

ФВ

Рис. 1
Исходные данные

a_min = –6,4 B;

a_max = 6,4 B;

F_c = 15*10³ Гц;

j = 79;

i = 5;

Вид модуляции АМ;

N₀ = 1,09·10^-7B²/Гц;

Способ приема когерентный.

Источник сообщений
Источник сообщений выдает сообщение а(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале а _min a _max распределены равномерно, а мощность сосредоточена в полосе частот от 0 до F_c.

Требуется:

1. 
   З аписать аналитические выражения и построить график одномерной плотности вероятности мгновенных значений сообщения а(t).
   
2. 
   Найти мат. ожидание и дисперсию сообщения а(t)
   
3. 
   Построить график случайного процесса и на графике обозначить max значение сигнала, математическое ожидание и среднеквадратичное отклонение.
   

1) Для непрерывных процессов Х(t) распределение вероятностей в заданный момент времени t₁ характеризуется одномерной плотностью вероятности (ПВ):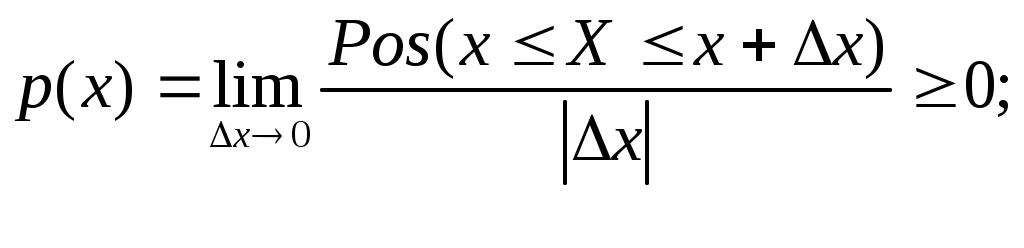



выражающей отношение вероятности того, что случайная величина Х(t) примет значения в интервале , к величине интервала .

Вероятность того, что случайная величина Х примет значение в интервале

(x_1,х₂) определяется выражением:


Из условия нормировки для достоверного события имеем:


В нашем случае ПВ имеет вид равнобедренного треугольника.





H







ПВ при треугольном распределении на интервале (а_min,a_max) изменяется по определенному закону и равна 0 вне этого интервала.



Где L длина основания треугольника:

;

L=12.8 В;

Высота треугольника H можно найти из условия нормировки т.к. площадь треугольника равна 1, то




Зная, что
Найдем высоту H:

;

;

Аналитическое выражение для треугольного закона распределения вероятности: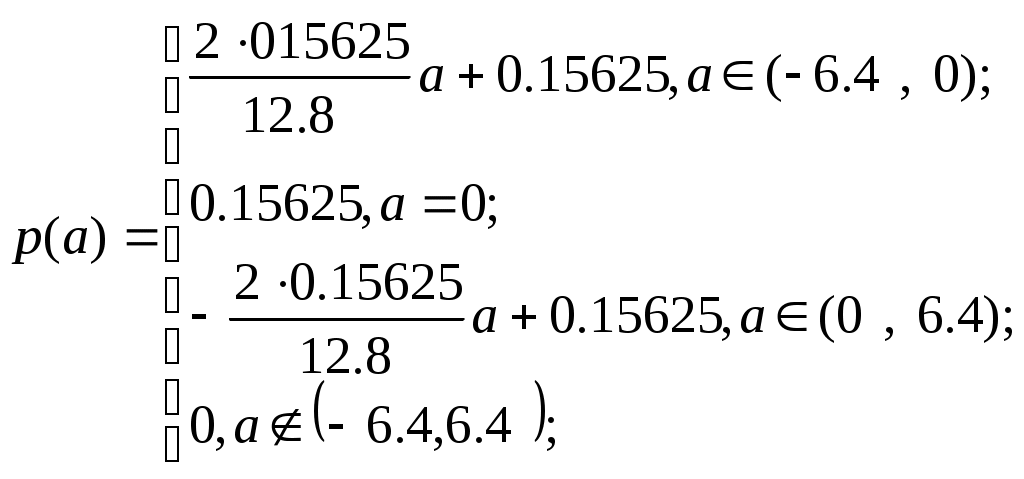



2) Математическое ожидание (МО) определяет среднее значение случайной величены

;

и для треугольного распределения ПВ имеет вид:




.

Дисперсия характеризует разброс случайной величены относительно ее среднего значения (физический смысл - средняя мощность отклонения от некоторой средней величины).


Для треугольного распределения ПВ:



Т.к. , получим:

В итоге =6.827 В².

Величину называют стандартным или среднеквадратическим отклонением (СКО).

=2.613 В.

3)


a_min = –6,4 B, a_max = 6,4 B, =2,613 В, =-2,613 В, .

Дискретизатор
Передача непрерывного процесса осуществляется дискретными методами. Для этого сообщение а(t) дискретизируется по времени и квантуется по уровню с равномерным шагом. Шаг квантования по уровню а= 0,1В.

Требуется:

1. 
   Определить шаг дискретизации по времени (t).
   
2. 
   Определить число уровней квантования (L).
   
3. 
   Рассчитать среднюю мощность шума квантования.
   
4. 
   Рассматривая дискретизатор как источник дискретного сообщения с объемом алфавита L, определить его энтропию и производительность (Н, Н^’), отсчеты, взятые через интервал t считать независимыми.
   

1) По теореме Котельникова, в полосе частот [0 , F_c] Гц шаг дискретизации по времени;

.

2) Число уровней квантования L при равномерном шаге определяется как частное от деления размаха сигнала на шаг квантования а. Число уровней квантования L равно:



3)Поскольку квантование по уровню производится с равномерным шагом , то закон распределения шума квантования также будет равномерным и не будет зависеть от номера интервала квантования. Тогда на интервале



МО (среднее значение шума квантования ) будет равно нулю, а средняя мощность (дисперсия шума квантования):



4)Энтропия – это средняя информативность источника на один символ, определяющая ‘неожиданность’ или ‘непредсказуемость’ выдаваемых им сообщений. Полностью детерминированный источник, выдающий лишь одну, заранее известную последовательность, обладает нулевой информативностью. Наоборот, наиболее ‘хаотический’ источник, выдающий

взаимно независимые и равновероятные символы, обладает максимальной информативностью.

Для источника, не обладающего памятью с алфавитом А энтропия записывается следующим образом:



Где L – объем алфавита , , i=1,2,3,…,L-вероятности выдачи источником символов , причем они не зависят от номера элемента последовательности, т.к. источник является стационарным.

Для треугольного распределения ПВ





Таким образам энтропия равна:

;

Если источник сообщения имеет фиксированную скорость символ/с, то производительность источника можно определить, как энтропию в единицу времени, (секунду):




Кодер
Кодирование осуществляется в два этапа.

Первый этап:

Производится примитивное кодирование каждого уровня квантованного сообщения – разрядным двоичным кодом.

Второй этап:

К полученной – разрядной двоичной кодовой комбинации добавляются проверочные символы, формируемые в соответствии с правилами кодирования по коду Хэмминга.

В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют символу «0», а отрицательные – символу «1» кодовой комбинации.

Требуется:

1. 
   Определить число разрядов кодовой комбинации примитивного кода , необходимое для кодирования всех L уровней квантованного сообщения.
   
2. 
   Определить избыточность кода при использовании кодирования Хэмминга.
   
3. 
   Записать двоичную кодовую комбинацию, соответствующую передаче j-го уровня, считая, что при примитивном кодировании на первом этапе j-му уровню ставится в соответствии двоичная кодовая комбинация, представляющая собой запись числа j в двоичной системе счисления. В полученной кодовой комбинации указать информационные и проверочные разряды.
   
4. 
   Определить число двоичных символов, выдаваемых кодером в единицу времени V_n и длительность двоичного символа T.
   

1)Для кодирования L =128 уровней квантованного сообщения число разрядов двоичной кодовой комбинации:

;

Число проверочных разрядов r для исправления однократной ошибки должно удовлетворять неравенству:

;

В итоге решение неравенства получаем r =4. Тогда длина всей кодовой комбинации:


2)Определим избыточность кода при использовании кодирования Хэмминга.



3) j=79 Его двоичная комбинация (занимающая К=7 разрядов). Проверочные символы располагаются позициях, где =0,1,2,…


1 0 0 1 1 1 1



b₁₁ b₁₀ b₉ b₇ b₆ b₅ b₃
Определим проверочные символы (они располагаются на 1,2,4,8 позициях):

b₁= b₃ b₅ b₇ b₉ b₁₁ r₁=b₁ b₃ b₅ b₇ b₉ b₁₁

b₂= b₃ b₆ b₇ b₁₀