Классическое определение вероятности. Геометрическое определение вероятности
 Скачать 63.86 Kb.
|
|
Классическое определение вероятности. Геометрическое определение вероятности. Вероятностью события А при данном испытании называется отношение числа благоприятных исходов к числу всех равновозможных исходов: 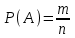 . (1)Геометрическое определение вероятности:
Действия над событиями. Какие события называются несовместными. Вероятность суммы произвольных событий, несовместных событий Определение 1. Суммой событий А, В называется третье событие С, состоящее в наступлении хотя бы одного из событий А, В: С = А + В Определение 2. Произведением двух событий А, В называется третье событие С, состоящее в одновременном наступлении этих событий: С = А · В Определение 3. Событие В называется противоположным событию А, если оно состоит не в наступлении события А: В = 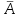 .События А, В называются несовместными, если они не могут произойти одновременно при данном испытании. Для несовместных событий справедлива формула Р (А + В) = Р (А) + Р (В). (6) Вероятность суммы несовместных событий равна сумме вероятностей этих событий. Вероятность суммы (объединения; появления одного из них, безразлично какого) двух произвольных событий равна сумме вероятностей этих событий за вычетом вероятности их совместного появления, т.е. P (A + B) = P (A) + P (B) - P (AB) Условная вероятность. Вероятность произведения произвольных событий, независимых событий. Вероятность противоположного события. Условная вероятность - Р(В/А) означает: вероятность события В при условии, что событие А наступило. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило. P (AB)=P (A)∙P(A/B). Если события независимы, получаем выражение теоремы произведения вероятностей независимых событий: P(AB)=P(A)·P(B) противоположными, если в данном испытании появление одного из них исключает появление другого и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают 1. Вероятность противоположного события можно вычислить по формуле: P (Ã)=1−P (A) Формула полной вероятности. Формула Байеса Перенесем эту задачу в следующую общую ситуацию: событие А может наступить при одной из n взаимоисключающих гипотез Н1, Н2, …, Нn. Рассуждая аналогично, применяя формулы сложения, умножения событий, получаем формулу Р(А) = Р(Н1) Р(А/Н1) +Р(Н2) Р(А/Н2) + … +Р(Нn) Р(А/Нn) которая называется формулой полной вероятности. 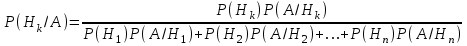 , которая называется формулой Байеса.Схема Бернулли. Функция Лапласа Ф(х), ее свойства. Интегральная и локальная формулы Муавра-Лапласа. При каждом испытании интересующее нас событие А (успех) наступает с вероятностью р и не наступает с вероятностью q = 1 – p. Такую ситуацию будем называть схемой с повторением испытаний или схемой Бернулли. 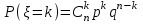 , k = 0, 1,…, n.для этого вначале введем функцию, которая называется функцией Лапласа и обозначается Ф(х): 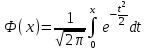 .10. Ф(0) = 0; 20. Ф (– х) = – Ф(х); 30. если | x| ≥ 3, то Ф (х) 0,5 с большой точностью. Для функции Лапласа имеются таблицы. P(m1 ≤ ≤ m2) 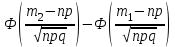 . Эта формула называется интегральной формулой Муавра-Лапласа При большом числе испытаний справедлива приближенная формула 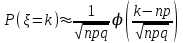 эта формула называется локальной формулой Муавра-ЛапласаДискретные и непрерывные случайные величины (с.в.). Закон распределения дискретной с.в Случайная величина называется дискретной, если она принимает отдельные изолированные значения, и непрерывной, если ее возможные значения заполняют сплошь промежуток на числовой оси или всю числовую ось. Законом распределения дискретной случайной величины называется таблица 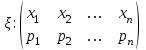 , где x1 а pk (k = 1, …, n) – их вероятности, то есть рk = P ( =хк). При этом должно выполняться равенство р1 + р2 + … + рn = 1. Это равенство означает, что при испытании одно из значений заведомо реализуется. Таблица показывает, как суммарная вероятность 100% распределяется по возможным значениям случайной величины. Математическое ожидание дискретной с.в., свойства Математическим ожиданием случайной величины называется число: М [ ] = m = x1· p1 + x2 · p2 + … + xn · pn (сумма произведений возможных значений на их вероятности). Свойства математического ожидания. 10. М [a] = а. Математическое ожидание неслучайной величины равно самой величине. 20. М [а ] = aM [ ]. Неслучайный множитель выносится за знак математического ожидания. 30. M [ + ] = M [ ] + M [ ]. Математическое ожидание суммы случайных величин равно сумме математических ожиданий. 40. Если , статистически независимы, то M[ · ] = M [ ] · M [ ]. Дисперсия дискретной с.в., свойства, СКО Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонений от центра: D [ ] = D = M [( – m)2] = p1 (x1– m)2 + p2 (x2– m)2 +…+ pn (xn – m)2. Свойства дисперсии: 10. D [a] = 0; 20. D [a ] = a2 D; 30. если , статистически независимы, то D [ + ] = D [ ] + D [ ]. 40. D = M [ 2] – 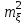 .Функция распределения с.в. (определение). Функцией распределения (вероятностей) случайной величины {\displaystyle X}X называют функцию F(x){\displaystyle F(x)}, значение которой в точке x{\displaystyle x} равно вероятности события {X<x}{\displaystyle \{X\leqslant x\}}, то есть события, состоящего только из тех элементарных исходов, для которых {\displaystyle X(\omega )\leqslant x} F (x) = p ( < x). Функция F(x) называется функцией распределения случайной величины . 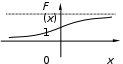 свойства функции распределения 10. 0 ≤ F (x) ≤ 1; 20. F (x) монотонно не убывает (рис. 11); 30. F (– ) = 0, F (+ ) = 1; 40. P (<< ) = F () – F (). Плотность распределения вероятности непрерывной с.в., ее свойства. Числовые характеристики непрерывной с.в. Плотностью вероятности случайной величины в точке х называется предел отношения вероятности попадания в отрезок [x, x + x] к длине отрезка x при условии, что отрезок стягивается к точке х:  .Свойства плотности вероятности: 10. f (x) ≥ 0 при всех х. 20. P ( (,)) = 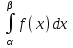 Числовые характеристики непрерывной случайной величины определяются формулами 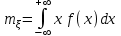 ;  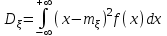;  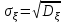.Связь между функцией и плотностью распределения Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле: f (x) = F′(x), то есть является производной функции распределения Основные законы распределения: Биномиальный - случайная величина называется биномиальной с параметрами (n, p), если она принимает значения 0, 1, 2, …, n и вероятности этих значений даются формулой 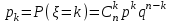 , k = 0, 1, …, n, q = 1 – p, p (0, 1).- закон Пуассона - случайная величина называется распределенной по закону Пуассона с параметром а, если она принимает любые целые неотрицательные значения и вероятности значений даются формулой 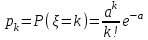 , k = 0, 1, 2,- равномерный, Непрерывная случайная величина называется равномерно распределенной на [a,b], если ее плотность вероятности дается формулой 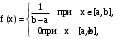 - показательный, Непрерывная случайная величина называется показательной, если ее плотность вероятности дается формулой 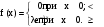 - нормальный - Непрерывную случайную величину называют нормальной с параметрами (a, ) и пишут = N (a, ), если ее плотность вероятности дается формулой 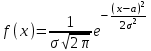 . |