Проверяемые задания. Практическая работа 1 определение суммы и вероятности события, сумма и произведение событий
 Скачать 57.14 Kb. Скачать 57.14 Kb.
|
ПРАКТИЧЕСКАЯ РАБОТА №1ОПРЕДЕЛЕНИЕ СУММЫ И ВЕРОЯТНОСТИ СОБЫТИЯ, СУММА И ПРОИЗВЕДЕНИЕ СОБЫТИЙЦель работы: ознакомиться с понятием о событии, вероятности события. Знания, приобретаемые студентами в результате освоения темы: понятие о теории надежности, отдельные положения теории вероятностей, применяемые в расчетах надежности изделии. Умения, приобретаемые студентами в результате освоения темы: определение суммы и вероятности события, суммы и произведения событий. Теория надежности является комплексной дисциплиной и состоит из таких разделов, как математическая теория надежности, надежность по отдельным физическим критериям отказов (физика отказов), расчет и прогнозирование надежности, обеспечение надежности на различных этапах жизненного цикла изделий, контроль надежности и техническая диагностика, теория восстановления работоспособности деталей машин, экономика надежности. Специфическая особенность надежности заключается в том, что точное значение ее показателей для конкретного изделия не может быть однозначно указано до начала эксплуатации. Значения всех показателей зависят от множества факторов, учесть которые практически невозможно. Сами факторы (например, действующие нагрузки, физико-механические характеристики материалов, допуски на размеры деталей и посадки сопряжений) имеют значительное рассеяние величин, что приводит к разбросу величин наработок, ресурсов, сроков службы, моментов наступления отказов однотипных изделий. Поэтому в расчетах надежности многие параметры должны рассматриваться как случайные величины, которые могут принимать то или иное значение, неизвестные заранее. Поэтому актуальной является задача рассмотрения отдельных положений теории вероятностей, применяемых в расчетах надежности изделий. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ События. В теории вероятностей различают следующие события: - достоверное, которое неизбежно происходит при каждой реализации данного комплекса условий (достоверным будет событие, если одна деталь, взятая из партии бракованных деталей, окажется бракованной); - невозможное, которое не может произойти при каждой реализации данного комплекса условий (невозможным будет событие, когда взятая из партии бракованных деталей окажется годной); - случайное, которое может произойти, а может и не произойти при каждой реализации данного комплекса условий (если в партии деталей содержатся как годные, так и бракованные детали, то событие, заключающееся в том, что взятая наугад деталь окажется бракованной, является случайным). Несколько событий могут быть: - независимыми, если вероятность проявления каждого из них не зависит от того, произошло ли другое событие (например, отказ двигателя и потеря работоспособности шины колеса – события независимые); - зависимыми, если вероятность проявления какого-нибудь из них меняется в зависимости от того, произошло ли другое событие или нет (например, разрушение подшипников коленчатого вала двигателя – событие А – произошло из-за отсутствия смазки в результате того, что отказал масляный насос – событие В. В этом случае событие А является зависимым от события В). - совместимым, если при выполнении комплекса условий они могут наступить одновременно; - несовместимыми, если одновременное их проявление в одном испытании или наблюдении невозможно (например, невозможно одновременное нахождение изделия в работоспособном и неработоспособном состояниях). События образуют полную группу, если во время опыта одно из них обязательно должно свершиться. Два несовместимых события, составляющих полную группу, называются противоположными (например, состояния исправности и неисправности объекта). Частость (или относительная частота) события W - отношение числа его проявлений к числу всех произведенных испытаний N, в каждом из которых это событие равновозможно: . 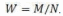 Вероятность события. Вероятность события А – Р(А) – отношение числа благоприятствующих этому событию исходов m к общему числу всех равновозможных несовместимых элементарных исходов n, образующих полную группу: 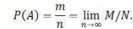 Вероятность любого события удовлетворяет двойному неравенству при этом вероятность события имеет следующие значения: - достоверного Р(А) = 1 (например, вероятность работоспособного со- стояния исправного автомобиля); - невозможного Р(А) = 0 (например, вероятность исправного состояния неработоспособного автомобиля); - случайного 0 < Р(А) < 1 (например, появление неисправности в процессе гарантийного срока эксплуатации автомобиля). Вероятность вычисляют до опыта и используют для прогноза надежности, а частность – после опыта и используют для анализа. Сумма и произведение событий. В теории надежности широко применяют такие понятия логической алгебры, как сумма и произведение нескольких, в частности двух событий. Суммой двух несовместимых событий А и В называется событие С, заключающиеся в появлении события А или В, безразлично какого (теорема сложения вероятностей). Вероятность появления одного или двух несовместимых событий, без- различно какого, равна сумме вероятностей этих событий Р(С) = Р(А+В) = Р(А) + Р(В) Сумма вероятностей двух событий, образующих полную группу, равна единице Р(А) + Р(В) = 1 Так как безотказная работа и отказ объекта составляют полную группу событий, то можно записать для любого момента времени эксплуатации ав- томобиля P(t) + Q(t) = 1, где P(t) – вероятность безотказной работы; Q(t) – вероятность отказа; t – наработка изделия. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Вероятность появления одного из нескольких попарно несовместимых событий, безразлично какого, равна сумме вероятностей этих событий Р(А + В +С) = Р(А) + Р(В) + Р(С) = Р(А + В) + Р(С) = = Р(А + С) + Р(В)= Р(В + С) + Р(А). Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий. Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти, или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Условной вероятностью РА(В) = Р(В│А) (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них и условной вероятности другого, вычисленной исходя из предположения, что первое событие уже наступило. Р(АВ) = Р(А)РА(В) = Р(В)РВ(А), где РА(В), РВ(А)- условные вероятности соответственно событий В и А. В частности, отсюда получаем РА(В) = Р(АВ)/ Р(А). Более применимой в теории надежности является теорема произведения вероятностей нескольких независимых событий. Всякая машина состоит из сборочных единиц и деталей, ряд из которых обеспечивает ее функционирование. Обычно машина будет работоспособна, если работоспособны все эти изделия. Вероятность работоспособного со- стояния машины равна вероятности совместного проявления работоспособного состояния всех указанных выше изделий. Р(АВС…N) = Р(А)Р(В)Р(С)…Р(N). Суммой двух совместимых событий А и В называется событие С, заключающееся в проявлении события А или В, безразлично какого или обоих вместе. Вероятность проявления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного проявления. Для независимых событий: Р(А + В) = Р(А) + Р(В) – Р(А)Р(В); Для зависимых событий: Р(А + В) = Р(А) + Р(В) – Р(А)РА(В). ПРИМЕРЫ Пример 1. При испытаниях на надежность группы невосстанавливаемых изделий время испытаний было разбито на четыре периода. Установлено, что вероятность отказа в период Т1 составила 0,15; в период Т2 – 0,45; в период Т3 – 0,3; в период Т4 – 0,1. Найти вероятность того, что наугад взятое изделие из группы отказало: 1) Либо в первый, либо в третий периоды испытаний; 2) Либо во второй или третий периоды испытаний. Так как отказы изделий в различные периоды испытаний являются со- бытиями несовместимыми (отказ изделия в какой-либо период исключает его отказ в другой период), то теорема сложения вероятностей применима. Искомая вероятность равна: 1) Р(Т1 + Т3) = 0,15 + 0,3 = 0,45; 2) Р(Т2 + Т3) = 0,45 + 0,3 = 0,75. Пример 2. В гараже находятся 3 белых машины и 2 черных. Из гаража выезжает одна машина, а затем вторая. Событие В – появление белой машины при первом выезде. Событие А – появление белой машины при втором выезде. Решение. Очевидно, что вероятность события А, если событие В про- изошло, будет РВ(А) = 2/4 = ½. Вероятность события А при условии, что событие В не произошло, будет РВ(А)=3/4. Пример 3. В гараже 3 белых и 3 черных машины. Из гаража дважды выезжают по одной машине, не возвращаясь обратно. Найти вероятность появления белой машины при втором испытании (событие В), если при первом испытании выехала черная машина (событие А). Решение. После первого испытания в гараже осталось 5 машин, из них 3 белых. Искомая условная вероятность РА(В) = 3/5 Этот же результат можно получить по формуле РА(В) = Р(АВ)/ Р(А) Действительно, вероятность появления белой машины при первом испытании Р(А) = 3/6 = 1/2. Найдем вероятность Р(АВ) того, что в первом испытании появится чер- ная машина, а во втором — белая. Р(АВ) = Р(А)РА(В) =1/2 × 3/5 = 3/10 Искомая условная вероятность 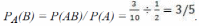 Результаты совпали. Пример 4. По статистике, из всех работ на ТО двигателей легковых автомобилей, поступающих на СТОА, 80% приходится на систему зажигания, 35% - на систему питания. Какова вероятность того, что очередному автомобилю, поступившему на станцию для ТО двигателя, потребуется проведение работ по ТО обеих систем либо только одной системы? События, заключающиеся в необходимости проведения работ по ТО систем зажигания и питания, являются независимыми друг от друга и совместимыми событиями. 1. Вероятность проведения работ по ТО системы зажигания Р(А) = 80/100 = 0,8 2. Вероятность проведения работ по ТО системы питания Р(В) = 35/100 = 0,35 3. Вероятность того, что очередному автомобилю, поступившему на станцию для ТО двигателя, потребуется проведение работ по ТО обеих систем Р(АВ) = 0,8×0,35 = 0,28 4. Вероятность того, что очередному автомобилю, поступившему на станцию для ТО двигателя, потребуется проведение работ по ТО только одной системы Р(А + В) = 0,8 + 0,35 – 0,28 = 0,87 ЗАДАНИЕ Изучить теоретическое обоснование и примеры определения суммы и вероятности события, суммы и произведения событий. 2. Решить следующие задачи. Задание 1. При испытаниях на надежность группы невосстанавливаемых изделий время испытаний было разбито на четыре периода. Установлено, что вероятность отказа в период Т1 составила 0,25; в период Т2 – 0,15; в период Т3 – 0,3; в период Т4 – 0,3. Найти вероятность того, что наугад взятое изделие из группы отказало: 1. Либо в первый, либо в третий периоды испытаний; 2. Либо во второй или четвертый периоды испытаний. Задание 2. В гараже находятся 6 белых машин и 5 черных. Из гаража выезжает одна машина, а затем вторая. Событие В – появление белой машины при первом выезде. Событие А – появление белой машины при втором выезде. Найти: 1. Вероятность события А, если событие В произошло. 2. Вероятность события А при условии, что событие В не произошло Задание 3. В гараже 6 белых и 4 черных машины. Из гаража дважды выезжают по одной машине, не возвращаясь обратно. Найти вероятность появления белой машины при втором испытании (событие В), если при первом испытании выехала черная машина (событие А). Задание 4. По статистике, из всех работ на ТО двигателей легковых автомобилей, поступающих на СТОА, 85% приходится на систему зажигания, 30% - на систему питания. Какова вероятность того, что очередному автомобилю, поступившему на станцию для ТО двигателя, потребуется проведение работ по ТО обеих систем либо только одной системы? |
