Курсовая работа - Расчет системы передачи дискретных сообщений. Курсовая работа по тэс расчет системы передачи дискретных сообщений Вариант ст гр. Мкс311 Котов Д

• Название: Курсовая работа по тэс расчет системы передачи дискретных сообщений Вариант ст гр. Мкс311 Котов Д
• Дата: 28.01.2022
• Размер: 1.09 Mb.
• Имя файла: Курсовая работа - Расчет системы передачи дискретных сообщений .doc
• Тип: Курсовая; #344661
• страница: 3 из 3

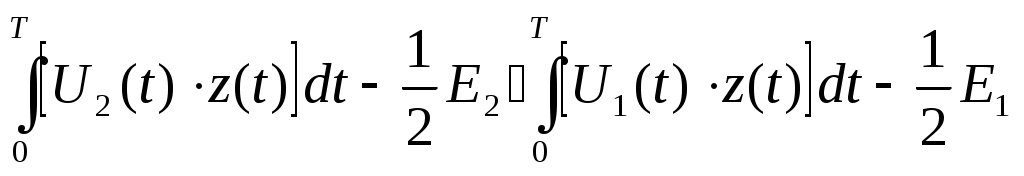Если неравенство выполняется , то приемник регистрирует “1”, в противном случае “0”.

Т.к. сигнал 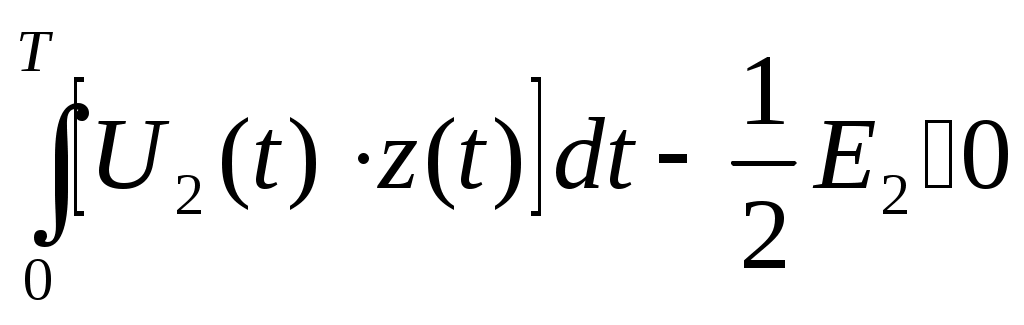, следовательно


()

2) Структурная схема оптимального когерентного демодулятора, реализующего неравенство *.

На схеме Х-перемножитель, интегратор, вычитающее устройство,

РУ-решающее устройство, определяющее в моменты времени кратные Т

максимальный сигнал.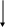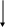










1

0

3) Вероятность ошибки р_ш оптимального когерентного демодулятора для канала с аддитивным нормальным белым шумом при передаче двоичных сообщений вычисляется следующим выражением:

р_ш= 1/2 (1-Ф(х)) ,

где Ф(х) – функция Крампа или интеграл вероятностей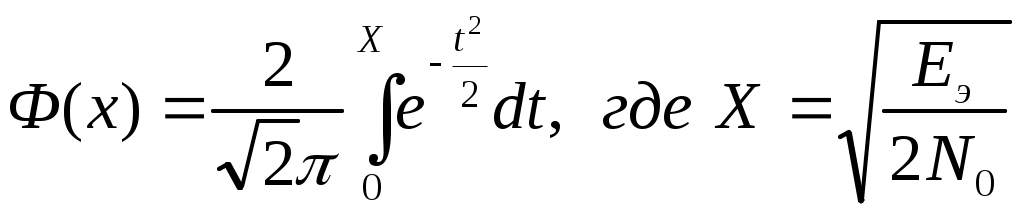



Е_э – эквивалентная энергия сигналов, определяется следующим образом: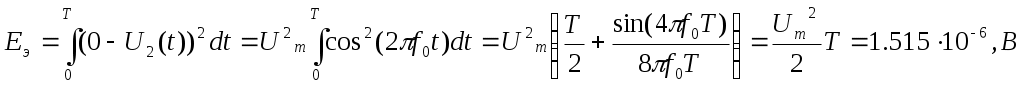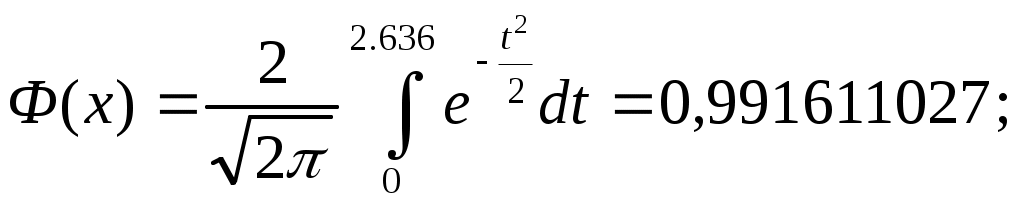







р_ш=0.5(1-0,991611027) =0,004194486;


4) ФМ является наиболее помехоустойчивым видом модуляции при равных энергетических затратах по сравнению АМ и ЧМ. Энергетический выигрыш ее составляет в четыре раза по сравнению с АМ и в два раза по сравнению с ЧМ.
Таблица сравнения.

Вид модуляции	По средней мощности	По пиковой мощности
ЧМ	1	2
ФМ	2	4
АМ	1	1

Декодер
В декодере декодирование осуществляется в два этапа. На первом этапе производится обнаружение и исправление ошибки в кодовой комбинации. Считать, что ошибка произошла в i-ом разряде. На втором этапе из нее выделяются информационные символы, а затем k – разрядная двоичная кодовая комбинация преобразуется в элемент квантованного сообщения.

Требуется:

1. 
   Оценить обнаруживающую способность q₀ кода Хэмминга.
   
2. 
   Записать алгоритм обнаружения ошибок.
   
3. 
   Определить вероятность не обнаружения ошибки.
   

1) По теореме Хемминга для того чтобы код позволял исправлять все ошибки в z (или менее) позициях , необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было:


Наш код исправляет одну ошибку и обнаруживает

ошибки.
2) Декодер получает от демодулятора некоторую последовательность двоичных символов b₁, b₂ ,b₃,…, b_i,…, b_n. В ней может быть ошибка.

Декодер позволяет исправить однократную ошибку и определить наличие

двукратной ошибки.

В декодере формируется т.н. проверочный синдром. По коду синдрома с помощью проверочной матрицы можно определить местоположение ошибки.
Кодовая последовательность: 10011111100 (j=79).

i=5 кодовая последовательность с ошибкой: 10011101100 .

Определим код синдрома.

1 0 0 1 1 1 0 1 1 0 0

b₁₁ b₁₀ b₉ b₈ b₇ b₆ b₅ b₄ b₃ b₂ b₁
r₁=b₁ b₃ b₅ b₇ b₉ b₁₁ r₁=1

r₂= b₂ b₃ b₆ b₇ b₁₀ b₁₁ r₂= 0

r₃= b₄ b₅ b₆ b₇ r₃= 1

r₄=b₈ b₉ b₁₀ b₁₁ r₄=0
r₁ r₂ r₃ r₄=1010=5₁₀

Т.о. разряд №5 является ошибочным. его инвертируем и получаем:

1 0 0 1 1 1 1 1 1 0 0
3) Вероятность не обнаружения ошибки определяется по формуле:

; ; где
n – число разрядов, ;

q-обнаруживающая способность кода Хэмминга, q=2.

р – вероятность ошибки в одном разряде, р=0,004194486 .

-общее число различных выборок объема .

.

Фильтр – восстановитель.
Фильтр–восстановитель – фильтр нижних частот с частотой среза F_c.

Требуется:

1. 
   Указать величину F_c.
   
2. 
   Изобразить идеальные АЧХ и ФЧХ фильтра – восстановителя.
   
3. 
   Найти импульсную характеристику g(t) идеального фильтра – восстановителя и начертить ее график.
   

1)Частота среза связана с временем дискретизации .Из теоремы Котельникова:



;

2)Передаточная функция идеального ФНЧ:

, где

j= ,

-АЧХ.

-ФЧХ.
Идеальная АЧХ фильтра – восстановителя имеет вид: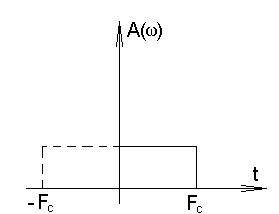



ФЧХ для идеального фильтра.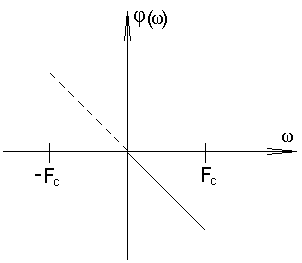



- время задержки (величина порядка 10^-4 – 10^-5 с).


3) Импульсная переходная характеристика берется как обратное преобразование Фурье: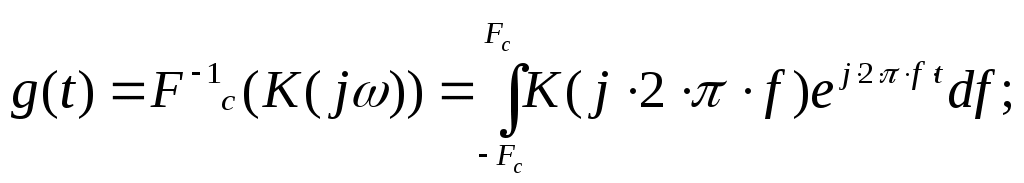



Будем считать, что фильтр работает на низких частотах и время задержки достаточно малая величина.

Если 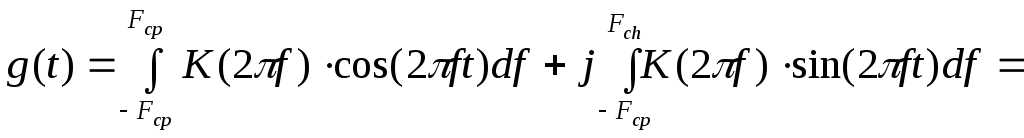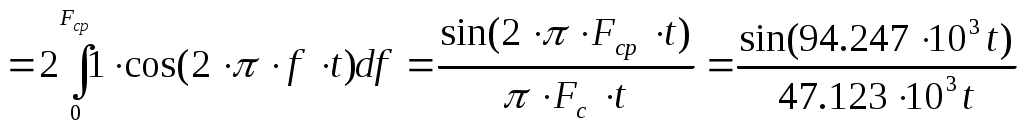=0, то , тогда



.

Таблица.

t,c	1	0.00002	0.000005	0.00006	0.00007	0.000075	0.000085
g(t)	0	1.009	1.926	-0.207	0.0936	0.2	0.246

График импульсной характеристики g(t).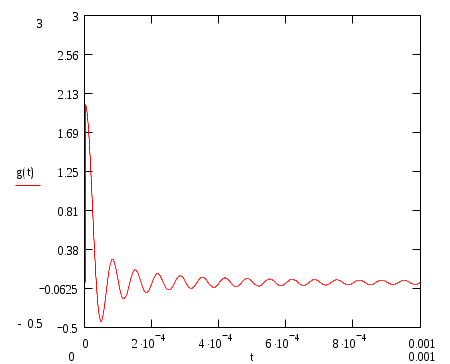


Таблица результатов.

H (высота),	, В	, В2	, с	L (число уровней)
0,15625	0	6.827	33.333·10-6	128
Ршк , В2	Н,	Н’,	n, (число разрядов)	,(избыточность кода)
8,33·10-4	6,722	201662.0166	11	0,3636
Vn,	Т, с	f, Гц	, Гц	, Гц
33·104	3.03·10-6	33·106	3.3·105	6.6·105
Рс , В2	Рш , В2	С,	рш	рно
0.25	0.03597	1974060	0.004194486	0,00001187