Курсовая работа - Расчет системы передачи дискретных сообщений. Курсовая работа по тэс расчет системы передачи дискретных сообщений Вариант ст гр. Мкс311 Котов Д

• Название: Курсовая работа по тэс расчет системы передачи дискретных сообщений Вариант ст гр. Мкс311 Котов Д
• Дата: 28.01.2022
• Размер: 1.09 Mb.
• Имя файла: Курсовая работа - Расчет системы передачи дискретных сообщений .doc
• Тип: Курсовая; #344661
• страница: 2 из 3

b₁₁ r₂= b₂ b₃ b₆ b₇ b₁₀ b₁₁

b₄= b₅ b₆ b₇ r₃= b₄ b₅ b₆ b₇

b₈= b₉ b₁₀ b₁₁ r₄=b₈ b₉ b₁₀ b₁₁

b₈ b₄ b₂ b₁ Проверочные символы:

1 0 0 0 1 b₁=0 r₁=0

2 0 0 1 0 b₂=0 r₂=0

3 0 0 1 1 b₄=1 r₃=0

4 0 1 0 0 b₈=1 r₄=0

5 0 1 0 1

6 0 1 1 0

7 0 1 1 1

8 1 0 0 0

9 1 0 0 1

10 1 0 1 0

11 1 0 1 1
В итоге получим кодовую комбинацию, содержащую информационные и проверочные разряды:

1 0 0 1 1 1 1 1 1 0 0
4) Число двоичных символов V_n , выдаваемых кодером в единицу времени,

определяется числом отсчетов в секунду ( ) и числом двоичных символов , приходящихся на один отсчет:

;

Длительность T двоичного символа определяется как :

;

Модулятор
В модуляторе синхронная двоичная случайная последовательность биполярных импульсов b(t) осуществляет модуляцию гармонического переносчика

U_m = cos(2πft), (U_m=1В, f = 100 V_n Гц)

При АМ «0» соответствует сигнал U₁(t) = 0,

символу «1» - U₂(t) = U_m cos(2πft).

Требуется:

1. 
   Записать аналитическое выражение модулированного сигнала U(t)=φ(b(t)).
   
2. 
   Изобразить временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передачи j-го уровня сообщения a(t).
   
3. 
   Привести выражение и начертить график корреляционной функции модулирующего сигнала В(τ).
   
4. 
   Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала G_b(f).
   
5. 
   Определить ширину энергетического спектра модулирующего сигнала ∆F_b из условия ∆F_b=αV_k (где α выбирается в пределах от 1 до 3). Отложить полученное значение ∆F_b на графике G_b(f).
   
6. 
   Привести выражение и построить график энергетического спектра G_u(f) модулированного сигнала.
   
7. 
   Определить ширину энергетического спектра ∆F_u модулированного сигнала и отложить значение ∆F_u на графике G_u(f).
   

1) Модуляция – изменение по заданному закону во времени величин, характеризующих какой-либо регулярный физический процесс. Под модуляцией колебаний понимают изменение амплитуды, частоты, фазы и т. д. В случае амплитудной модуляции (АМ) несущее колебание промодулировано по закону изменения амплитуды первичного сигнала. Несущее колебание – это синусоидальное колебание высокой (несущей) частоты, амплитуда которого модулируется передаваемым сигналом.

Модулятор, составная часть передатчика в каналах электросвязи, с помощью которой осуществляется управление параметрами гармонических электромагнитных колебаний, т. е. модуляцией колебаний. Управляющий элемент модулятора – транзистор, электронная лампа, клистрон, ячейка Керра и т. д.


Аналитическое выражение для АМ модулированного сигнала:

;

;

.

2) Временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передачи j-го уровня сообщения a(t).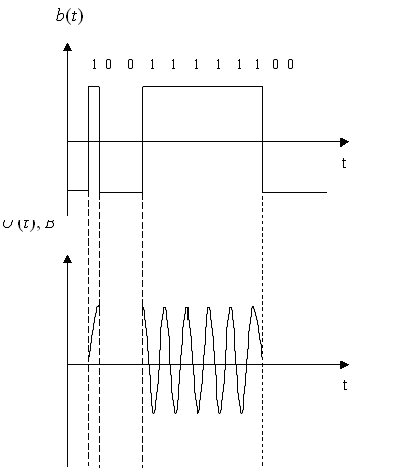


3) Корреляция, в математической статистике – вероятностная или статистическая зависимость. Корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов.

Корреляционная функция дает качественное представление о линейной зависимости между значениями одной или двух случайных функций в выбранные моменты времени.

Свойства корреляционной функции:

1. 
   Корреляционная функция четна:
   
2. 
   Абсолютное значение автокорреляционной функции при любых не может превышать значения при =0.
   

 корреляционная функция имеет максимум при =0.

 абсолютное значение корреляционной функции ограничивается значением дисперсии.

3. 
   Случайные процессы, наблюдаемые в стационарно устойчиво работающих системах имеют конечное время корреляции:
   

Корреляционная функция случайного синхронного телеграфного биполярного сигнала с единичной высотой импульсов имеет следующий вид: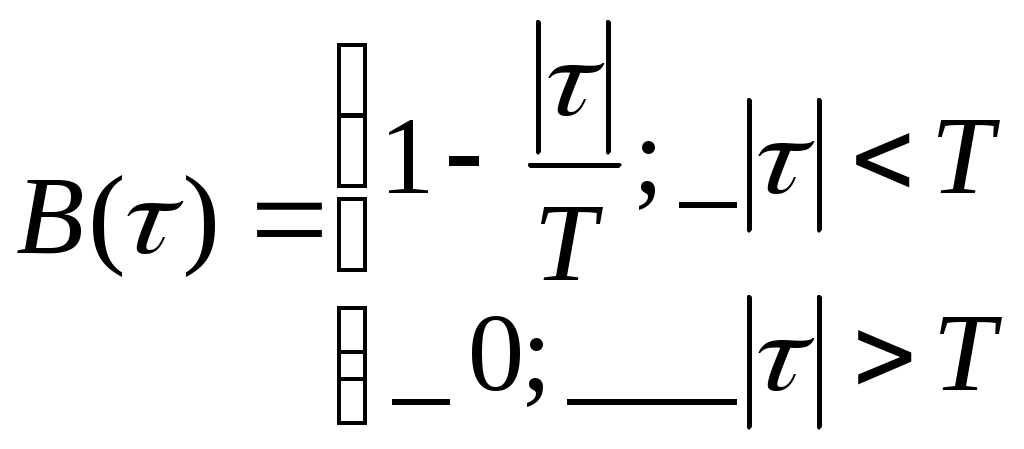

, где T длительность импульсов.















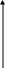4) Спектральная плотность величины – предел отношения величины (напряжения, мощности и др.), соответствующий узкому участку оптического спектра, к ширине этого участка.

Для нахождения спектральной плотности мощности G_b(f) сигнала b(t) необходимо воспользоваться теоремой Хинчина - Винера, которая устанавливает связь между энергетическим спектром корреляционной функцией случайного процесса.
Спектральная плотность мощности модулирующего сигнала G_b(f):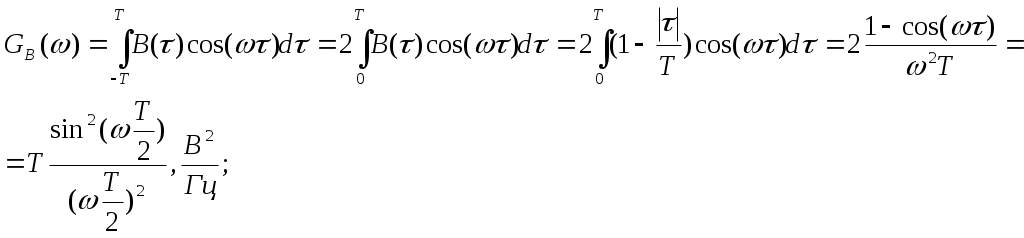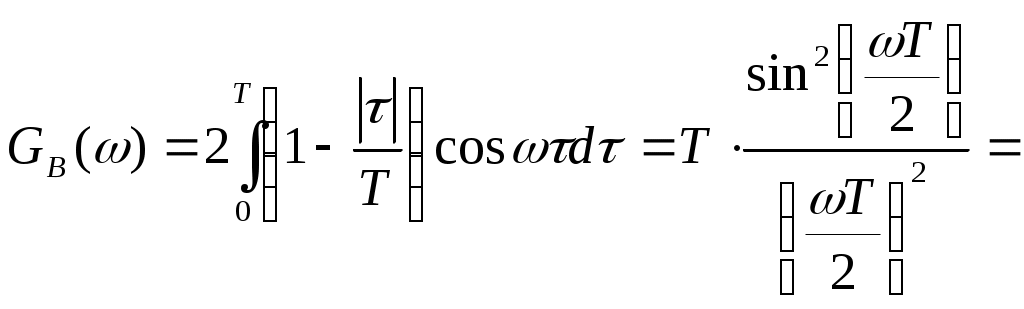








График спектральной плотности мощности модулирующего сигнала G_b(f):

Gb(f),B2/Гц	3.0310-6	9.74310-9	1.33510-7	9.39510-9	4.37310-8	2.96210-10
f,Гц	1	3.5105	5105	7105	8.5105	106

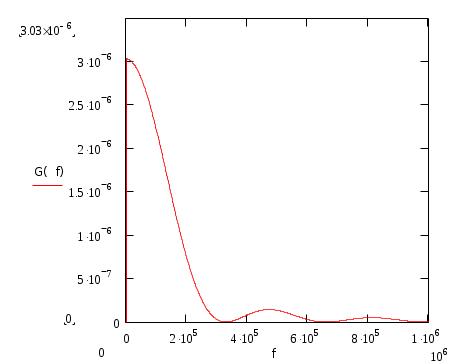5) На графике видно , что вся энергия модулирующего сигнала сосредоточена в полосе ∆F_b Гц.



6) График спектральной плотности мощности модулированного сигнала G_b(f).: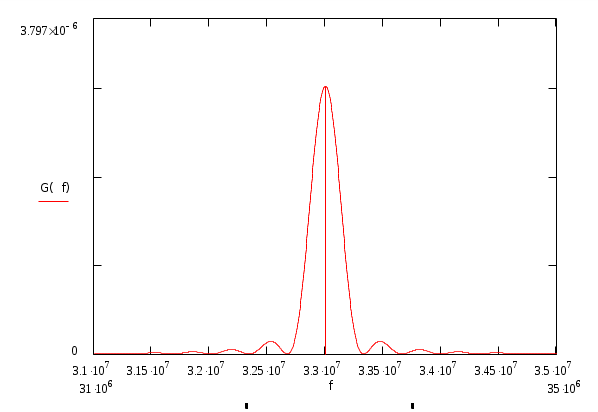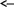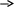



В результате модуляции исходный спектр сдвигается на частоту модулируемого колебания. Если известен спектр модулирующего сигнала , можно найти спектр амплитудно-модулированного сигнала. Энергетический спектр амплитудно-модулированного сигнала содержит -функцию на частоте f=f₀ верхнюю и нижнюю боковые полосы. Наличие -функции в энергетическом спектре отражает наличие несущей частоты при амплитудной модуляции. Форма верхней боковой полосы энергетического спектра АМ сигнала совпадает с формой энергетического спектра модулирующего сигнала b(t), а форма нижней – совпадает с зеркальным спектром сигнала b(t).
7) Ширина энергетического спектра при АМ будет в два раза больше ширины энергетического спектра модулирующего сигнала.



Канал связи
Передача сигнала U(t) осуществляется по каналу с постоянными параметрами и аддитивным флуктуационным шумом n(t) с равномерным энергетическим спектром N₀/2 (белый шум).

Сигнал на выходе такого канала можно записать следующем образом:

z(t) = U(t) + n(t) , U(t)- полезный сигнал, n(t)- аддитивная помеха.
Требуется:

1. 
   Определить мощность шума в полосе частот F_k = ∆F_u ;
   
2. 
   Найти отношение сигнал – шум Р_с /Р_ш;
   
3. 
   Найти пропускную способность канала С;
   
4. 
   Определить эффективность использования пропускной способности канала К_с, определив ее как отношение производительности источника Н^’ к пропускной способности канала С.
   

1) В каналах связи аддитивные помехи возникают по различным причинам и могут принимать различные формы, индивидуальные реализации которых трудно учесть. Такие помехи чаще вызывают необратимые изменения передаваемых сигналов. Аддитивные помехи по своей структуре разделяют на три основных класса: распределенные по частоте и времени (флуктуационные), сосредоточенные по частоте (квазигармонические) и сосредоточенные во времени (импульсные).

Флуктуационные помехи порождаются в системах связи случайными отклонениями тех или иных физических величин (параметров) от их средних значений. Источником такого шума в электрических цепях могут быть флуктуации тока, обусловленные дискретной природой носителей зарядов.

Наиболее распрастраненной причиной шума в аппаратуре связи являются флуктуации, обусловленные тепловым движением.

Зная спектральную плотность мощности N₀ можно определить мощность шума Р_ш в полосе ∆F_u (промодулированного сигнала).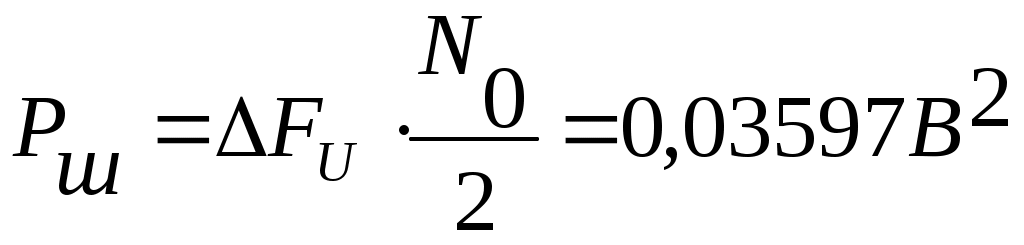
;

2) При определенном отношении , для двоичных равновероятных сигналов U₁(t) и U₂(t) их средняя мощность будет ровна:

, В²;

где и , где T- длительность сигналов.

Символу “0” cоответствует сигнал ;

Символу “1” cоответствует сигнал ;

Если передается “0” то ;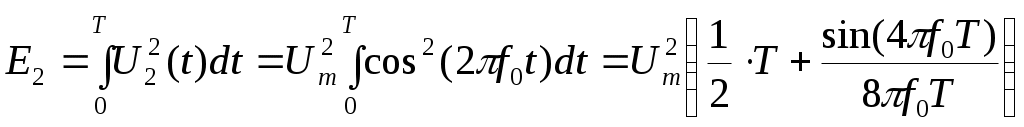

;
Так как , поэтому ;

;


3) Под пропускной способностью понимают количество, данных которое может быть передано по каналу за 1 секунду.

;

4) Эффективность использования пропускной способности канала К_с:



Демодулятор
В демодуляторе осуществляется оптимальная когерентная или некогерентная (в зависимости от варианта) обработка принимаемого сигнала z(t) = U(t) + n(t)

Требуется:

1. 
   Записать алгоритм оптимального приема по критерию минимума средней вероятности ошибки при равновероятных символах в детерминированном канале с белым гауссовским шумом.
   
2. 
   Нарисовать структурную схему оптимального демодулятора для заданного вида модуляции и способа приема.
   
3. 
   Вычислить вероятность ошибки р_ш оптимального демодулятора.
   
4. 
   Определить, как нужно изменить энергию сигнала, чтобы при других видах модуляции и заданном способе приема обеспечить найденное значение вероятности ошибки р_ш.
   

1)Канал с аддитивным гауссовским шумом отображается линейной цепью с постоянной передаточной функцией, сосредоточенной в определенной полосе частот. Допустимы любые входные сигналы, спектр которых лежит в определенной полосе частот F_c , имеющие ограниченную среднюю мощность Р_с (либо пиковую мощность Р_пик).

Предположим , что все искажения в канале строго детерминированы и случайным является только гауссовский белый аддитивный шум со спектральной плотностью N₀. Это значит что при передаче символа “1”

принимаемое колебание можно записать математической моделью z(t) = U₂(t) + n(t) , где U₂(t)- известный переносчик для символа “1”. Передаче символа “0” соответствует известный переносчик U₁(t): z(t) = U₁(t) + n(t).

Неизвестна реализация помехи и позиция (индекс 1 или 2), переданного сигнала , который и должна распознать решающая схема. Распознавание осуществляется на основе метода идеального наблюдателя (Котельникова).

Для когерентного приемника границы начала и конца принимаемого сигнала

точно известны, т.е. передаваемые сигналы финитны и имеют одинаковую длительность, а в канале нет ни многолучевого распространения, ни линейных искажений, вызывающих увеличение длительности сигнала (либо они скорректированы).

В таком случае алгоритм приема, который осуществляет оптимальный приемник над входным колебанием, имеет вид: