ПДС. Шапагатов А.С. 8 прак. Задача Дана кодовая комбинация g x
 Скачать 13.47 Kb. Скачать 13.47 Kb.
|
|
Задачи для самостоятельного решения. Задача 8.4. Дана кодовая комбинация G(x7+x5+x4+x2). Построить циклический код на базе образующего полинома Р(x3+x+1) с использованием двух методов. Умножаем G(x) на Хm, который имеет третью степень, получим: (x7+x5+x4+x2)*X3=x10+x8+x7+x5=10110100000 Разделив произведение G(x)Хm на образующий многочлен Р(Хm), согласно получим: (x10+x8+x7+x5)/(x3+x+1)=(x7+x2)+  или в двоичном эквиваленте: 10110100000/1011=10000100+ 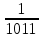 Таким образом, в результате получаем частное Q(x) той же степени, что и G(x): G(x7+x2)= 10000100 и остаток: R(x2)=100 В итоге комбинация двоичного кода, закодированная циклическим кодом, согласно примет вид: и остаток: F(x)= 10000100*1011=110101100+100=110101000 Переданная кодовая комбинация F(x)= 110101000, построенная с помощью образующего полинома Р(х)=1011. Под воздействием помехи кодовая комбинация трансформировалась в комбинацию F(x)= 100101000. 100101000/1011 =1 1010(100) Наличие остатка 101 свидетельствует об ошибке. Однако он не указывает непосредственно на место ошибки в комбинации. Для определения ошибки существует несколько методов, основанных на анализе синдрома. Рассмотрим один из них. Число сдвигов равно одному. Это означает, что ошибка в элементе а2. Исправленная кодовая комбинация имеет вид 110101000, то есть соответствует переданной. |
