хуй. Практическое занятие 2 теоретический материал и примеры решения. 1. цифРОвая пеРЕДАча анаЛОГОвых сигНАлов
 Скачать 152.56 Kb. Скачать 152.56 Kb.
|
|
1. ЦИФРОВАЯ ПЕРЕДАЧА АНАЛОГОВЫХ СИГНАЛОВ А 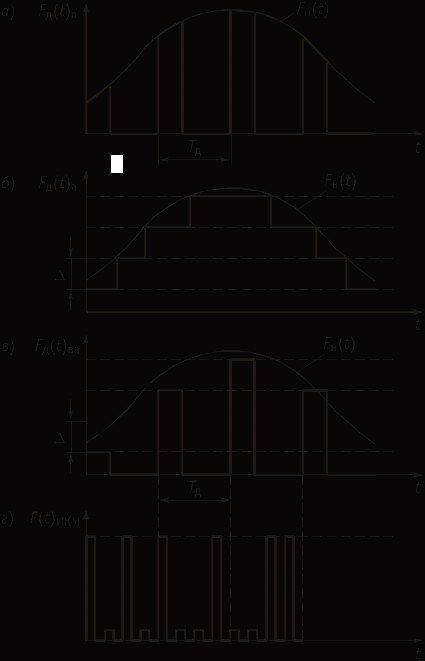 Рисунок 1.1 - Дискретные сигналы: а – дискретный по времени; б – дискретный по уровню; в – дискретный по времени и по уровню; г – цифровой сигнал с ИКМ налоговым сигналом в системах передачи называется непрерывный электрический или оптический сигналы, параметры которого (амплитуда, частота или фаза) изменяются по закону непрерывной функции времени источника информации, например: речевого сообщения, подвижного или неподвижного изображения и т.д. 2. ПРИНЦИПЫ ФОРМИРОВАНИЯ КАНАЛЬНОГО ЦИФРОВОГО СИГНАЛА с ИКМ 2.1. Дискретизация во времени Преобразование непрерывного аналогового сигнала в дискретный может быть осуществлено в соответствии с теоремой отсчетов, доказанной В.А. Котельниковым в 1933 г.: любой непрерывный сигнал с ограниченным частотой FМАКС спектром, может быть полностью представлен в виде своих дискретных во времени отсчетов, взятых через интервал времени Тд 1/2Fмакс, называемый периодом дискретизации. Технически операция дискретизации по времени осуществляется при помощи ключевых схем путем получения сигналов с амплитудно-импульсной модуляцией (АИМ). При АИМ амплитуда периодической последовательности импульсов изменяется в соответствии с изменением амплитуды модулирующего непрерывного сигнала Fн(t). Различают амплитудно-импульсную модуляцию первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 амплитуда отсчетов, следующих с частотой дискретизации Fд=1/Tд=1/2Fмакс, изменяется в соответствии с изменением модулирующего сигнала Fн(t) на интервале времени передачи отсчета tи, а при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего сигнала в начальный момент отсчета. На рисунке 2.1 представлен исходный модулирующий сигнал Fн(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации сигнала. 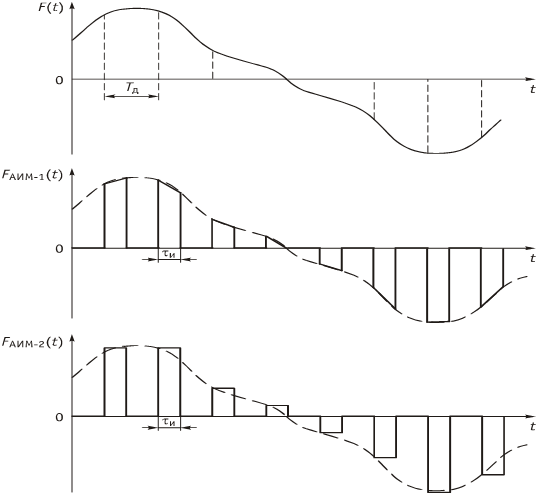 Рисунок 2.1 - Формирование АИМ сигнала Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму Вид частотного спектра G(f) для АИМ сигнала при Тд >>t приведен на рисунке 2.2. 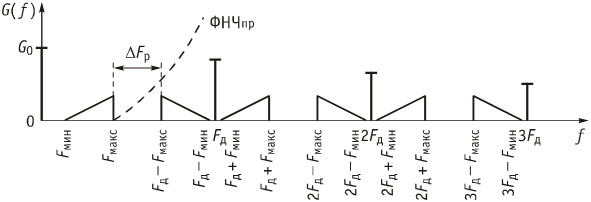 Рисунок 2.2 - Спектральный состав АИМ сигнала Из рисунка 2.2 видно, что для восстановления исходного непрерывного сигнала из АИМ сигнала, на приеме достаточно поставить ФНЧ (или фильтр-интерполятор) с частотой среза, равной Fмакс, который выделит исходный сигнал. Основным параметром ФНЧ является Относительная ширина переходной полосы ФНЧ (или иначе ее называют относительная ширина полосы расфильтровки фильтра), которая определяется выражением 2.1: 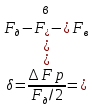 , (2.1) , (2.1)2.2. Квантование по уровню Как видно из рисунка 2.2, АИМ-сигнал является дискретным во времени, но непрерывным по уровню, так как амплитуда отсчетов может принимать бесконечное множество значений. Однако любая аппаратура обработки сообщений и систем передачи имеет конечную разрешающую способность. Это связано как с ошибками, возникающими при обработке сигналов, так и с наличием шумов и искажений в аппаратуре и каналах передачи. В связи с этим нет необходимости передавать все бесконечное множество амплитудных значений непрерывных сигналов, его можно ограничить конечным множеством, содержащим определенное, заранее установленное, для того или иного вида сигналов, число «разрешенных» амплитудных значений. Эти «разрешенные» для передачи амплитудные значения сигнала называются уровнями квантования; выбор их количества определяет качество передачи сигналов. При квантовании по уровню весь возможный динамический диапазон сигнала от Uмакс до Uмин разбивается на разрешенные уровни (если электрический сигнал передается в виде АИМ напряжения непрерывного сигнала: F(t) = U(t)). Разность между двумя соседними разрешенными для передачи уровнями называется шагом квантования D. Если амплитуда отсчета сигнала UАИМ(t) в пределах двух соседних разрешенных значений превышает половину шага квантования D/2, ее значение увеличивается в большую сторону, если меньше половины шага квантования – в меньшую сторону. Таким образом получается сигнал квантованный по уровню – Uкв(t). Разность между истинным значением отсчета и его квантованным значением называется ошибкой квантования, или шумом квантования, и определяется формулой 2.2. ш кв(t) = UАИМ(t) – Uкв(t), (2.2) Произведя «нумерацию» уровней квантования можно передавать не сами уровни, а их значения по шкале уровней в двоичном коде. В этом случае на приеме восстановить квантованный по уровню сигнал достаточно просто. Уровень квантованного сигнала на приеме определяется формулой 2.3. Uкв(t)пр = li × D, (2.3) где li= (0, lмакс) – номер разрешенного уровня в десятичной системе счисления; D – шаг квантования; 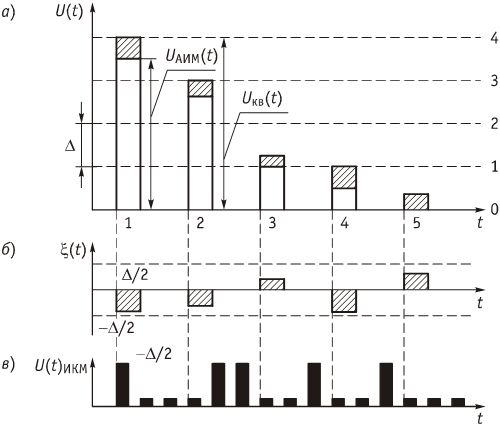 Рисунок 2.3 - Принципы квантования по уровню и формирования канального сигнала с ИКМ Мощность шумов квантования определится формулой 2.4. 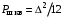 , (2.4) , (2.4)2.3. Кодирование Операция кодирования заключается в преобразовании номера «разрешенного» уровня в кодовую комбинацию двоичной системы счисления, состоящую из m символов вида «0» и «1», где величина m называется разрядностью кода. Существует большое число двоичных систем кодирования, однако в ЦСП с ИКМ нашли применение натуральный двоичный код и его модификация – симметричный двоичный код [11]. При использовании натурального кода любое положительное десятичное число li, не превышающее величины lмакс 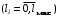 , может быть представлено в виде комбинации из m двоичных символов по следующему алгоритму (формула 2.5): , может быть представлено в виде комбинации из m двоичных символов по следующему алгоритму (формула 2.5):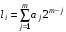 , где , где 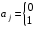 , (2.5) , (2.5)гдеm – разрядность кода. Очевидно, что lмакс определяется суммой весовых составляющих вида 2 m – j при значении всех коэффициентов аj = 1 и определяется формулой 2.6: lмакс = 2 m – 1, (2.6) а суммарное число «разрешенных» уровней квантования (учитывая, что кодируется и ноль) формулой 2.7: lS = lмакс + 1 = 2 m, (2.7). Связь между числом разрядов m и числом уровней квантования определяется соотношениями: m = log2 (lS), (2.8) Поскольку при передаче телефонных сигналов в каналах ЦСП с ИКМ используется двухполярное кодирование (для устранения постоянной составляющей и гармонических частот вида kFд, 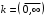 ), в указанных ЦСП используется симметричный двоичный код, в котором 1 или 0 в старшем разряде определяют полярность кодируемого сигнала с АИМ. ), в указанных ЦСП используется симметричный двоичный код, в котором 1 или 0 в старшем разряде определяют полярность кодируемого сигнала с АИМ.Проиллюстрируем процесс кодирования при помощи простейшего примера. Пусть разрядность натурального двоичного кода m = 4. Тогда образующий полином примет вид: 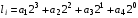 , ,при этом lмакс = 24 – 1 = 15, l∑ = 16, т.е. при помощи 4-х разрядной кодовой комбинации можно закодировать не более 16 «разрешенных» уровней с номерами от 0 до 15. Предположим, что номер «разрешенного» уровня li = 11, тогда двоичная комбинация в натуральном коде будет иметь вид: 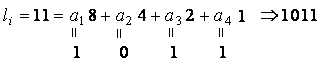 При помощи симметричного двоичного кода первым символом кодовой комбинации кодируется знак отсчета. При одинаковой разрядности кода m натуральный и симметричный коды обеспечивают кодирование одинакового числа уровней квантования. Например, при m = 4, при помощи симметричного кода можно закодировать также как и при помощи натурального кода 16 «разрешенных» уровней, но с номерами от +0 до +7 и от –0 до –7. В современных ЦСП с ИКМ операции квантования по уровню и кодирования на передаче реализуются в одном устройстве, называемом кодером: на его вход подается сигнал с АИМ-2, на выходе формируется цифровой двоичный сигнал с ИКМ. На приеме осуществляется обратное преобразование при помощи декодера. Примеры решения задач Задача 1 Выбрать частоту дискретизации, определить переходную полосу частот и относительную ширину переходной полосы ФНЧ при дискретизации сигналов вещания первого класса с диапазоном частот 0,05 ... 10 кГц. Решение: На основании теоремы Котельникова : следовательно, в нашем случае Fд>20 кГц. В современных системах передачи Fд = (примерно 2,3 или 2,4) * 2Fв. Частота дискретизации это целое число, обычно кратное 4. Ответ: Fд =24 кГц Для телефонного сигнала стандартная частота дискретизации Fд = 8 кГц. При организации канала вещания (вместо трех телефонных каналов) частота дискретизации сигналов вещания должна быть кратна частоте дискретизации телефонного канала и равна 8х3=24 кГц, что не противоречит условию выбора (2,2…2,4)Fв. Переходная полоса частот (полоса расфильтровки) для ФНЧ определяется из спектра АИМ сигнала (рисунок 2.8) по формуле 2.4: DFр = (Fд – Fмакс) – Fмакс = 24 – 10 – 10 = 4 кГц 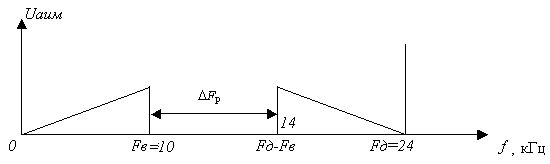 Рисунок 2.4 - Спектр АИМ-сигнала Относительная ширина переходной полосы ФНЧ (относительная ширина полосы расфильтровки ФНЧ) определяем по формуле 2.3: 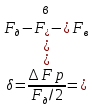 = 0,33 = 0,33Ответ: Fд = 24 кГц; DFр = 4 кГц; 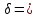 0,33. 0,33.Задача 2 На вход канала ЦСП подается сигнал в спектре (0,3 - 5,4) кГц. Частота дискретизации выбрана равной Fд=8 кГц. Какая часть спектра сигнала на выходе канала окажется искаженной? Решение: Определяем спектр АИМ сигнала (рисунок 2.9): Fн = 0,3 кГц; Fв = 5,4 кГц; Fд = 8 кГц; Fд – Fн = 8 – 0,3 = 7,7 кГц; Fд - Fв = 8 – 5,4 = 2,6 кГц  Рисунок 2.5 - Спектра АИМ сигнала Рисунок 2.5 - Спектра АИМ сигнала Ответ: искаженной окажется часть спектра от 2.6 кГц до 5.4 кГц. Задача 3 Закодировать отсчет напряжения сигнала с помощью простого натурального кода, если UАИМ = 20,6 mB, D = 0,5 mB, m = 6. Определить ошибку квантования. Решение: 1. Определяем номер уровня квантования: l = Uаим/D, подставляем значения и получим l = 20,6/0,5 = 41,2 = 41 2. Определяем разрядность натурального кода согласно формуле 2.21: m = log2 41 @ 6 3. Определяем коэффициенты двоичного кода: l = 41 = 125 + 024 + 123 + 022 + 021 + 120 = =132 + 016 + 18 + 04 + 02 + 11 следовательно, получим кодовую комбинацию: 4110 = 1010012 4. Определяем квантованное значение сигнала согласно формуле 2.6: Uкв= l× D = 41 × 0,5 = 20,5 mB. 5. Определяем ошибку квантования: x = UАИМ – Uкв = 20,6 – 20,5 = 0,1 mB < Δ/2 = 0,25 mB Ответ: x = 0,1 mB, 101001. Задача 4 Определить число уровней квантования для минимально допустимого значения Акв = 25 дБ, если пик-фактор сигнала Q = 35 дБ. Решение: 1. Определяем разрядность кода m = (Акв + Q – 5,58)/6 @ 10 согласно формуле 2.23. 2. Определяем число уровней по формуле 2.20: l = 210 = 1024. Ответ: N = 1024. Задача 5 Закодировать отчеты напряжения аналогового сигнала с помощью симметричного кода, если UАИМ1 = 25,2 mB, UАИМ2 = –26,8 mB, ∆ = 0,5 mB, m = 7. Решение: Определяем номер уровня квантования: l = Uаим/D l1 = Uаим1 /D = 25,2/0,5 = 50,4 = 50 l2 = Uаим2 /D = -26,8/0,5 = - 53,6 = - 54 2. Определяем коэффициенты двоичного кода при m = 7. Так как у нас код симметричный, то первый (старший) разряд будет указывать положительный или отрицательный уровень квантования: «0» – отрицательный, а «1» – положительный уровень. l 1 = 50 = 125 + 124 + 023 + 022 + 121 + 020 = = 132+ 116 + 08 + 04 + 12 + 01, получаем 1110010. l 2 = -54 = - (12 5+ 124 + 023 + 122 + 121 + 020) = = - (132 + 116 + 08 + 14 + 12 + 01), получаем 0110110. Ответ: 1110010, 0110110. Задача 6 Определить амплитуду и знак отсчета аналогового сигнала, переданного с системы передачи с ИКМ с помощью симметричного кода в виде кодовой комбинации 11100110, если Δ = 0,1 mB. Решение: Определяем номер уровня квантования lиз кодовой комбинации 11100110. Так как у нас код симметричный, то первый (старший) разряд 1 будет указывать на положительный уровень квантования. Исключаем ее из процесса декодирования. l = 11001102 = 126 + 125 + 024 + 023 + 122 + 121 + 020 = = 164 + 132 + 016 + 08 + 14 + 12 + 01 = 10210, получаем номер уровня квантования равный +102. Определяем значение амплитуды сигнала Uаим = l × D: Uаим = 102 × 0,1 = 10,2 mB. При декодировании сигнала для компенсации ошибки квантования в декодере к амплитуде декодированного сигнала добавляется значение равное Δ/2. В нашем случае Uаим вых = 10,2 + 0,05 = 10,25 mB Ответ: Uаим вых = 10,25 mB |
