Формулировка задач. 1 Даны два числа. Найти среднее арифметическое кубов и среднее геометрическое модулей этих чисел
 Скачать 17.44 Kb. Скачать 17.44 Kb.
|
|
1) Даны два числа. Найти среднее арифметическое кубов и среднее геометрическое модулей этих чисел. 2) Найти (в радианах и градусах) все углы треугольника со сторонами а, b, c 3) Мальчик, продающий на улице газеты, зарабатывает А руб. на продаже каждой из первых 35 газет. На каждой из остальных проданных газет он зарабатывает по Х руб. Напишите программу, которая выведет заработок мальчика, если он продаст B газет. 4) Присвоить переменным Х и Y два числа. Вывести: Для чисел _____ и _____ Сумма = _______ 5) Вычислить значения по следующим формулам при действительных значениях всех переменных: 1. ln |cos x| ln (1+x2) 2. (x+1x-1)x+18xy2 6) Создать модель анализа пожарного датчика в помещении и вывода сообщения «Пожароопасная ситуация». Температура вводится с клавиатуры и должна быть больше 60°С. 7) Рис расфасован в два пакета. Масса первого — m [кг], второго —n[кг]. Определить, какой пакет тяжелее и какова масса более тяжелого пакета. 8) Проанализировать возраст человека, чтобы отнести к одной из четырех групп: дошкольник, ученик, работник, пенсионер. Возраст вводится с клавиатуры. 9) Определить, пройдет ли график функции у = ах2 + bх + с через заданную точку с координатами (m, n). 10) Вычислить значения следующих функций: 1. F(x)={x2- x при 0≤x≤1 x2-sin x2 при x>1 или х<0 2. F(x)={-x2+х-9 при x≤8 1x4-6 при x<8 11) По введенному номеру времени года (1 — зима, 2 — весна, 3 — лето, 4 — осень) получить соответствующие этому времени года месяцы и число дней в каждом месяце. 12) В старояпонском календаре был принят двенадцатилетний цикл, годы внутри которого назывались соответственно: крыса, 28 корова, тигр, заяц, дракон, змея, лошадь, овца, обезьяна, курица, собака и свинья. По введенному номеру некоторого года получить его название по старояпонскому календарю. (Для справки: 1996 г. — год крысы и начало очередного цикла.) 13) Дано натуральное число n. Вычислить S=132+152+172+…+1(2n+1)2 14) Вычислить у = x10+2x9+3x8+ ... + 10х + 11 15) Числа Фибоначчи (fn) определяются формулами f0=f1и fn=fn-1+fn-2 при n=2,3… Найти fp 16) Дано натуральное число n. Вычислить у = 1 *3 *5 *...х*(2n - 1). 17) Дан массив действительных чисел с размерностью N. Определить, сколько в нем отрицательных, положительных и нулевых элементов. 18) Дана последовательность действительных чисел а1, а2..., аn. Поменять местами наибольшее и наименьшее числа. 19) Вычислить сумму квадратов элементов последовательности. 20) Определить среднее арифметическое элементов последовательности. 21) Написать метод, вычисляющий значение xn/(n+x). С его помощью вычислить выражение: 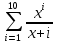 22) Даны координаты вершин треугольника АВС. Найти его площадь. |
