деревья. 1. Деревья поиска. Общее определение, сбалансированность, высота, виды деревьев
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
1. Деревья поиска. Общее определение, сбалансированность, высота, виды деревьев В информатике дерево поиска — это древовидная структура данных, используемая для поиска определенных ключей из набора. Для того, чтобы дерево функционировало как дерево поиска, ключ для каждого узла должен быть больше любых ключей в поддеревьях слева и меньше любых ключей в поддеревьях справа. Преимуществом деревьев поиска является их эффективное время поиска, учитывая, что дерево достаточно сбалансировано, то есть листья на обоих концах имеют сопоставимую глубину. Существуют различные структуры данных дерева поиска, некоторые из которых также позволяют эффективно вставлять и удалять элементы, операции с которыми затем должны поддерживать баланс дерева. Поиск данных, являясь одним из приоритетных направлений работы с данными, предполагает использование соответствующих алгоритмов в зависимости от ряда факторов: способ представления данных, упорядоченность множества поиска, объем данных, расположение их во внешней или во внутренней памяти. Поиск – процесс нахождения конкретной информации в ранее созданном множестве данных. Как правило, данные представляют собой структуры, каждая из которых имеет хотя бы один ключ – значение определенного поля конкретной структуры. Ключ поиска – это поле, по значению которого происходит поиск. Уменьшить число сравнений ключей с эталоном возможно, если выполнить организацию дерева особым образом, то есть расположить его элементы по определенным правилам. При этом в процессе поиска будет просмотрено не все дерево, а отдельное поддерево. Такой подход позволяет классифицировать деревья в зависимости от правил построения.  Высота дерева — это самый длинный путь вниз от его корня до любого доступного листа. Высота дерева — это самый длинный путь вниз от его корня до любого доступного листа.Временная сложность операции над двоичным деревом поиска, обычно основаны на его высоту. Таким образом, деревья с n узлами могут быть построены таким образом, что поиск займет 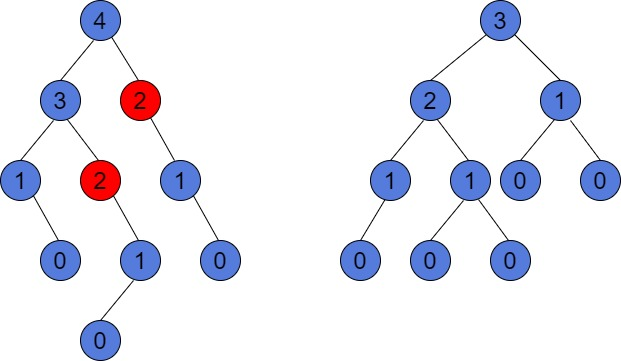 Бинарное дерево сбалансировано, если для каждого узла высоты его левого и правого дочерних элементов отличаются не более чем на 1. Если у узла нет ни одного из дочерних элементов, то высота отсутствующих дочерних элементов равна -1. 2. Деревья поиска. Бинарное дерево поиска, операции Двоичное дерево представляет собой в общем случае неупорядоченный набор узлов, который либо пуст (пустое дерево) либо разбит на три непересекающиеся части: узел, называемый корнем; двоичное дерево, называемое левым поддеревом; двоичное дерево, называемое правым поддеревом. Таким образом, двоичное дерево — это рекурсивная структура данных. Каждый узел двоичного дерева можно представить в виде структуры данных, состоящей из следующих полей: данные, обладающие ключом, по которому их можно идентифицировать; указатель на левое поддерево; указатель на правое поддерево; указатель на родителя (необязательное поле), удобно для удаления. Значение ключа уникально для каждого узла. У каждого узла ключ и два сына; В левом поддереве ключи меньше, а в правом – больше; Если ключи поступают в случайном порядке, то глубина дерева будет O(log N); если дерево “неудачное(например, с возрастающими числами)”, то его глубина будет O(n); Рассмотрим выполнение основных операций над деревьями поиска: поиск узла в дереве, вставка узла в дерево, удаление узла из дерева. 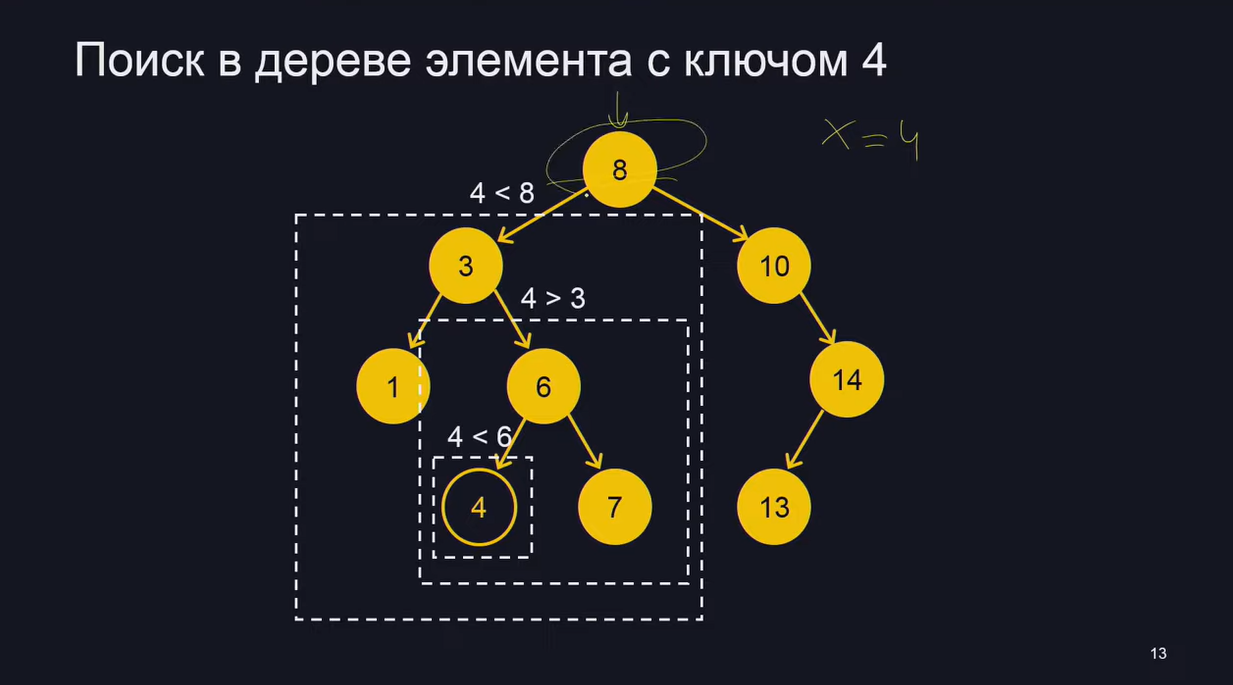 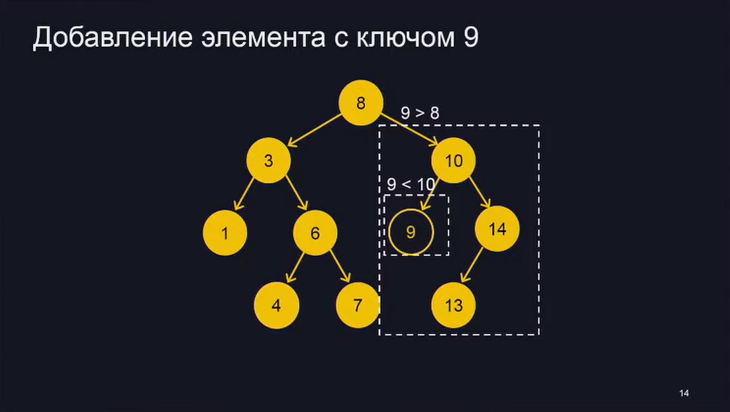 Для удаления – освобождаем память, где хранилась 4, возвращаемся к предпоследнему элементу (используя указатель на родителя), и потомка, который нашелся, заменяем на указатель (условно, типа bool), что этого потомка нет. Первый шаг необходим, чтобы найти в дереве вершину, которая должна быть удалена. Третий шаг представляет собой обратный проход от места, из которого взят элемент для замены удаляемого, или от места, из которого удален элемент, если в замене не было необходимости.  - Любой элемент из поддерева, где есть число 14, будет больше, чем число 10. 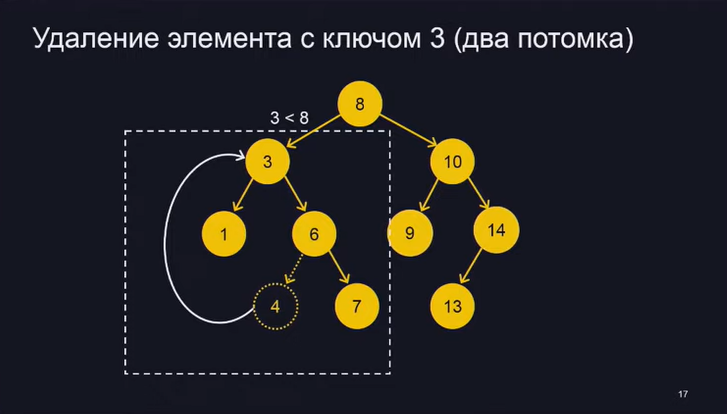 - Заменим 3 на первое число, которое больше, чем эта 3 (идем в правое поддерево и ищем самый левый элемент). 3. Деревья поиска. AVL-дерево, операции Для АВЛ-деревьев сбалансированность определяется разностью высот правого и левого поддеревьев любого узла. Если эта разность по модулю не превышает 1, то дерево считается сбалансированным. Данное условие проверяется после каждого добавления или удаления узла. АВЛ-деревом называется такое дерево поиска, в котором для любого его узла высоты левого и правого поддеревьев отличаются не более, чем на 1. Эта структура данных разработана советскими учеными Адельсон-Вельским Георгием Максимовичем и Ландисом Евгением Михайловичем в 1962 году. Аббревиатура АВЛ соответствует первым буквам фамилий этих ученых. Первоначально АВЛ-деревья были придуманы для организации перебора в шахматных программах. Советская шахматная программа «Каисса» стала первым официальным чемпионом мира в 1974 году. В каждом узле АВЛ-дерева, помимо ключа, данных и указателей на левое и правое поддеревья (левого и правого сыновей), хранится показатель баланса – разность высот правого и левого поддеревьев. В некоторых реализациях этот показатель может вычисляться отдельно в процессе обработки дерева тогда, когда это необходимо. |
