Шпоры по электротехнике. 1. Электрическая цепь (ЭЦ), элемент эц, электрическая схема. Источники и приемники электрической энергии

• Название: 1. Электрическая цепь (ЭЦ), элемент эц, электрическая схема. Источники и приемники электрической энергии
• Анкор: Шпоры по электротехнике
• Дата: 26.02.2023
• Размер: 0.69 Mb.
• Имя файла: Shpory_po_elektrotekhnike_1.doc
• Тип: Документы; #955695
• страница: 1 из 4

1. Электрическая цепь (ЭЦ), элемент ЭЦ, электрическая схема. Источники и приемники электрической энергии.

ЭЦ – совокупность приборов и устройств, процессы в которых могут быть описаны при помощи понятий (ЭДС, сопротивление, напряжение и ток).

Элемент электрической цепи – устройство или прибор, выполняющий определенные функции.

Все элементы электрической цепи принципиально делятся на источники и потребители:

1. Источники электрической энергии – элементы, в которых различные виды энергии преобразуются в электрическую (генераторы (механическая в электрическую); термопары (тепловая энергия в электрическую); солнечные батареи (световая в электрическую); аккумуляторы и гальванический элемент (химическая в электрическую)).

2. Потребители (приемники) электрической энергии - элементы электрической цепи, в которых электрическая энергия преобразуется в другие виды энергии (двигатель (электрическая в механическую энергию); гальванические ванны (в химические связи); нагреватели (в тепловую энергию); лампы ( световая энергия)).

3. Вспомогательные элементы – выключатели, предохранители, разъемы, измерительные приборы.

Схема – графическое изображение электрической цепи.

Чаще всего используются электрические схемы 3-х видов:

1. Монтажная схема - изображает элементы цепи и соединительные провода.

2. Принципиальная схема – на ней показываются условные графические изображения элементов и их соединений.

3. Схема замещения – расчетная модель электрической цепи, на которой элементы замещаются идеализированными элементами без вспомогательных элементов, не влияющих на результаты расчетов.

Источники (генераторы) электрической энергии подразделяются на: Источники тока;

Источники ЭДС.

Идеальные источники электрической энергии – элементы, внутренние потери в которых

отсутствуют.

Идеальные источники ЭДС – элемент, напряжение, на зажимах которого, может

представлять любые функции во времени, но не зависящего от тока, протекающего ч/з

него.

Реальные ИЭ всегда имеют внутренние потери, то есть источники ЭДС имеют внутреннее сопротивление, а источники тока – внутреннюю проводимость (величина, обратная сопротивлению).
2. Классификация электрических цепей (ЭЦ). Закон Ома для участка цепи, содержащего источник ЭДС.

ЭЦ делятся:

1.цепи постоянного тока (ток, не меняющ. во времени), цепи переменного тока (синусоидально изменяющийся ток).

2.Линейные – ЭЦ сопротивление каждого эл-та кот. не зависит ни от тока, ни от напряжения. Зависимость напряж. от тока показывается на вольт-амперных хар-ках.

Нелинейные – если хотя бы один элемент в цепи имеет сопротивление, зависящее или от тока или от напряжения

3.Простые - цепь, в которой все элементы цепи соединены последовательно. Сложные – все остальные.
Топологические элементы электр. схем. Ветвь – участок цепи, на кот. все эл-ты соединены последовательно. Узел – точка пересеч. 3-х и более ветвей. Контур - путь от обхода вдоль ветвей ЭЦ начин. и заканч. в одн. т. (На рис. – 2 узла, 3 контура, 3 ветви)
З-н Ома на участке цепи: I=U_ab/R. Напряжение на любом участке цепи, соединяющей источники ЭДС = произведению протекающего через участок тока на сопротивление этого участка: U_ab=IR.

Общий закон Ома для участка цепи, в которой присутствуют источники ЭДС:

U_ab=IR U_cb=c-b; E=b-c =>c-b=-E=U_cb;

Uab=Uac+Ucb; U_ab=IR-E;

I=(U_ab+E)/R – для участка цепи, соединяющей источники ЭДС.

U_ab=IR U_ab=а-b=E


3. Схемы замещения реальных источников энергии. Режимы работы источников энергии. Баланс мощностей в цепи постоянного тока.
1. Схема замещения с использованием источника ЭДС.

r ₀ – внутреннее сопротивление источника.

Е – ЭДС идеального источника ЭДС.

2. Схема замещения с использованием идеального источника тока.

I – ток источника тока.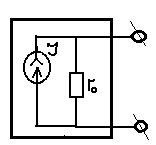


Обе схемы замещения эквивалентны по отношению к нагрузке тогда, когда выполняется условие: Е=Ir₀

Энергия и мощность электр.цепи

Из определения ЭДС , что работа совершаемая источником энергии за время t, те работа сторонних сил по разделению зарядов равна W_и=EQ=EIt. На нагрузке при напряжении U и токе I расходуется энергия W_п=UQ=UIt=RI²t=U²t/R

Мощность Р характеризует иньенсивность преобразования энергии из одного вида в другой в единицу времени , мощность источника P_и=W_и/t=EI , для приемника P_п=W_п/t=UI=RI²=U²/R

В СИ мощность измеряют в ДЖ и ВАТТ, 1 ДЖ=1Ватт*сек

Баланс мощностей в цепях постоянного тока:

На основании закона сохр энергии -Сумма мощностей приемников электрической цепи равна сумме мощностей источников электрической энергии:


и сточник ЭДС является потребителем или приемником электрической энергии, в том случае, если направление его ЭДС и ток через него не совпадают. Такой источник энергии входит в правую часть баланса мощностей со знаком минус.

4. Законы Кирхгофа. Расчет цепей постоянного тока путем непосредственного применения законов Кирхгофа. Потенциальная диаграмма

Законы:

1. Алгебраическая сумма токов в узле равно 0.
Т 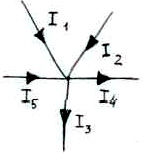оки, втекающие в узел берутся с "+", вытекающие с "-"

(I₁+I₂-I₃-I₄+I₅=0).

Если в схеме имеются n-узлов, то для нее можно составить (n-1) независимых уравнений по 1 закону Кирхгофа.

2. Алгебраическая сумма падений напряжений вдоль замкнутого контура равна алгебраической сумме ЭДС вдоль этого контура.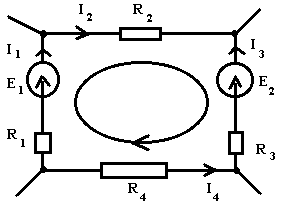






Падение напряжения на элементах, входящих в контур, считать положительным, если направление тока через элемент совпадает с выбранным нами направлением обхода контура. Также и ЭДС.

I₁R₁+I₂R₂-I₃R₃-I₄R₄=E₁-E₂
непосредственного применения законов Кирхгофа:

Пусть p – количество ветвей, n – количество узлов, k – количество ветвей, содержащих источники тока, q – количество уравнений, составленных по второму закону Кирхгофа, m – количество уравнение, составленных по первому уравнению Кирхгофа.

m=n-1; q=p-(n-1)-k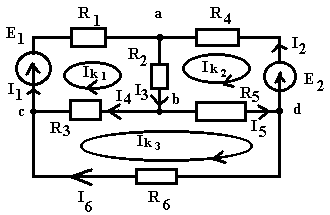



Потенциальная диаграмма: Строится для любого замкнутого контура, при этом потенциал одной (любой) из точек контура принимается равным нулю. По оси абсцисс последовательно откладывается сопротивление всех элементов, входящих в контур, а по оси ординат – потенциалы различных точек контура.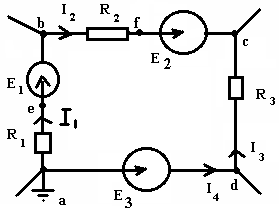


7. Расчет цепей постоянного тока методом контурных токов и методом эквивалентного генератора.

М 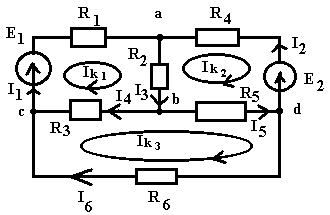етод контурных токов:

Пусть в каждой ветви контура протекает контурный ток.

I1=I_k1;

I2=-I_k2;

I3=I_k1-I_k2;

I4=I_k1-I_k3;

I5=I_k3-I_k2;

I6=I_k3;

С 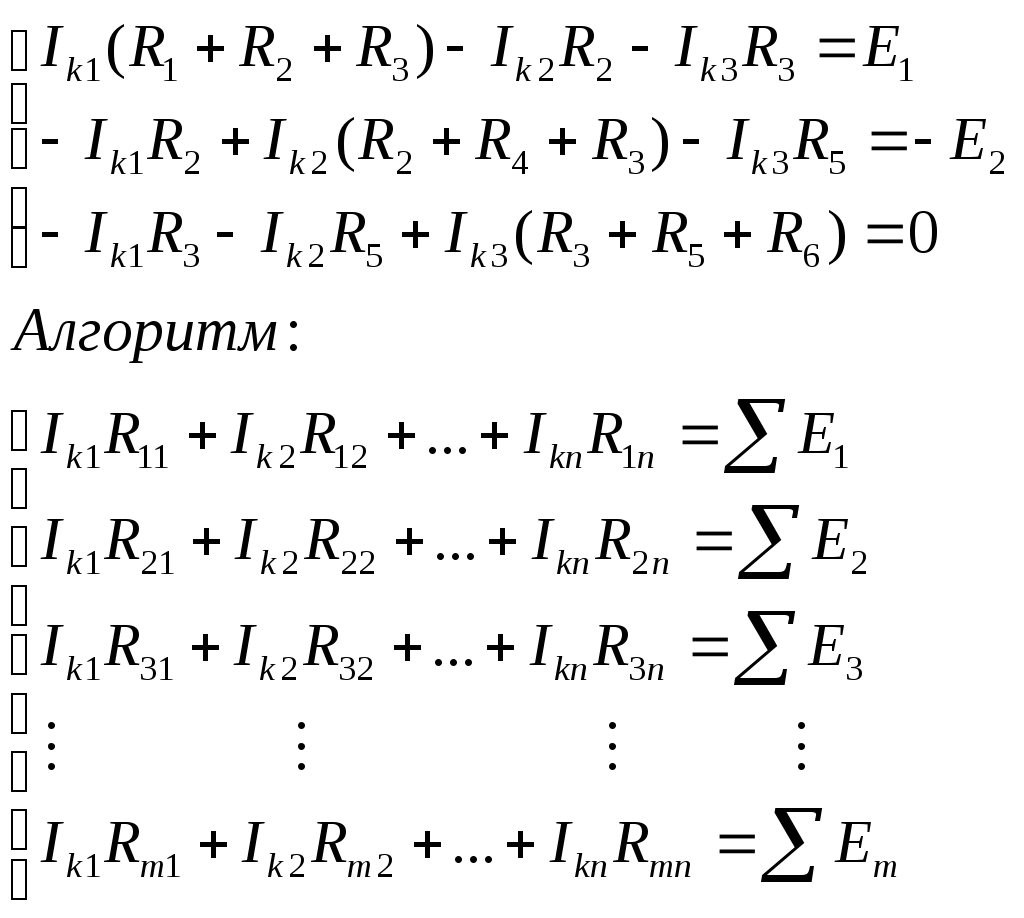опротивления вида R₁₁, R₂₂, R_mn (m=n) называются собственными сопротивлениями контура и представляют собой сумму всех сопротивлений, входящих в контур.

Сопротивления вида R_km (k≠m) – это сопротивление общей ветви для контурных токов I_k и I_m. Оно считается положительным, если направление контурных токов через общую ветвь совпадает.

8. Метод эквивалентного генератора:

Позволяет найти ток в отдельно взятой ветви сложной цепи.

Суть: выделяется ветвь, в которой требуется найти ток, а вся оставшаяся цепь представлена в виде эквивалентного генератора, который характеризуется ЭДС и внутренним сопротивлением.

п орядок расчета:

1. 
   разрывается ветвь, в которой требуется найти ток, и находится (любыми достижимыми методами) напряжение между точками разрыва – напряжение холостого хода (Uxx)
   
2. 
   определяется внутреннее сопротивление эквивалентного генератора, при условии, что источники энергии в нем отсутствуют и заменены их внутренними сопротивлениями.
   
3. 
   находим ток.
   

Цепи однофазного пересенного тока.
1. Получение синусоидальной ЭДС. Основные величины, характеризующие гармонические колебания.

Цепью синусоидального тока называется цепь, токи напряжения и ЭДС на всех участках которой изменяются по синусоидальному закону с одинаковой частотой.

Значение переменного тока (напряжение и ЭДС) в любой момент времени (заданный) называется мгновенными значениями тока.

П олучение синусоидальной ЭДС:

з-н Максвелла.

е=-dФ/dt

Ф_n=BScosα=BScos(ωt+φ)

е=BSωsin(ωt+φ)=E_msin(ωt+φ)
Основные величины, характеризующие гармонические колебания:

a 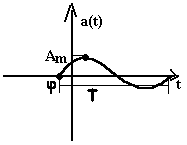(t)=A_msin(ωt+φ)

A_m – амплитуда колебаний

(ωt+φ) – фаза колебаний

ω – угловая частота.

ω=2πf, где f – частота колебаний; f=1/T

Т – период колебаний.

Период – время, за которое величина совершает полное колебание.
В 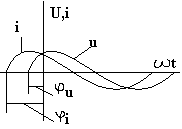цепях переменного тока напряжение и ток, изменяясь по синусоидальному току с одинаковой частотой, в общем виде имеют разные начальные фазы колебаний. Разность между начальными фазами колебаний напряжения и тока называется сдвигом фаз между ними.

φ=φ_u-φ_i


3. Представление синусоидальных функций в различных формах.

Способы изображения:

1. 
   аналитическая форма:
   
2. 
   представление в виде вращающихся векторов:
   
3. 
   комплексный или символический метод: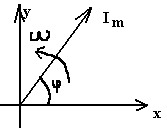
   

обычно записываются комплексы действующих значений синусоидальных величин.
к 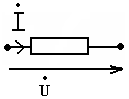омплексным сопротивлением элемента называется отношение комплекса напряжения на элементе к комплексу тока через него.

- комплексное сопротивление

2. Действующие и средние значения синусоидальных величин

под действующим значением синусоидальной величины понимают среднеквадратичное значение за период колебаний.
для тока:

I – постоянный ток, i – синусоидальный (переменный) ток.
действующее значение синусоидального это такое значение постоянного тока, которое на единичном сопротивлении за время, равное одному периоду колебания, выделит такое же количество тепла, как и переменный ток.

Среднее значение синусоидально изменяющейся величины называется ее среднеарифметическое значение за "+" полупериод.

10. Резистивный элемент в цепи переменного тока. Векторная диаграмма.

Резестивный элемент в цепи перем. тока.

I=U/R

векторная диаграмма – совокупность векторов напряжений и токов на комплексной плоскости.

Комплексное сопротивление резистивного элемента = его активному сопротивлению. Напряжение на резистивном элементе и ток через него совпадают по фазе т.е.=0.
11. Конденсатор в цепи переменного тока. Векторная диаграмма.

Комплексное сопротивление емкостного элемента.

Конденсатор в цепи переменного тока.

q=СU q-заряд, U –напряжение, C-емкость;

напряжение на конденсаторе отстает по фазе от тока через него на угол 90⁰

Емкостное сопротивление Х_с=1/wC ; U= -jX*_cI

12. Индуктивность в цепи переменного тока. Векторная диаграмма. Комплексное сопротивление индуктивного элемента.

Индуктивность цепи переменного тока.

Индуктивность – это коэффициент, который связывает потокосцепление катушки и ток.

=Li;

Потокосцепление: =Ф₁n₁+Ф₂n₂+…+Ф_kn_k;

n_k – кол-во витков сцепленных с магнитным потоком Ф_k.

ЭДС катушки при изменении потокосцепления:

e=-d/dt; U_i=-e_i=d/dt=Ldi/dt;

i=I_msin(t); U_L=I_mLcos(t)=I_mLsin(t+90);

В комплексном виде: I=I_me^j0=I_m; U=I_mLe^j90=U_me^j90;;

Комплексное сопр. катушки индуктивности: Z=(I_mLe^j90)/I_m=Le^j90=Х_Le^j90;

величина Х_L=L – индуктивное сопротивление.
Комплексные плоскости: Для мгновенных значений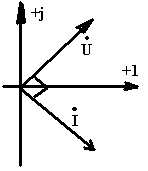



Напряж-е на индуктив-м эл-те опережает ток на угол 90 U= -jX*_LI
13. Законы Кирхгофа в комплексной форме и для мгновенных значений.

Комплексный метод расчета цепей переменного тока.

1.Синусоидальные колебания тока и напряжения, а также сопротивления элементов заменяются их изображением в комплексном виде.

2. Определяются комплексы неизвестных напряжений и токов при помощи законов Ома и Кирхгофа.

3 . По изображениям найденных величин в комплексном виде получают их оригинал.
Z=R (1)

Z=jL=jX_L (2)

Z=-j/C=-jX_C (3)

Закон Ома в компл-ном виде:

I=U/Z;

Законы Кирх. в компл-м виде:

I=0 – сумма компл. токов в узле =0.

E=IZ – cумма компл. напр-ий в замкн. контуре=сумме комплексов ЭДС в этом контуре.

З-ны Кирх. для мгновен. Знач:

Алгер-я сумма мгновен. знач. токов в узле равна нулю: i=0

Алгебр сумма напряж на резистивных, ёмкостных и индуктивных эл-х контура в каждый момент времени = алгебр. сумме ЭДС в контуре в тот же момент времени. U_R=iR; U_L=Ldi/dt;
14. Резонанс напряжений. Векторная диаграмма.

Резонансные явления в цепи переменного тока.

Резонанс – такой режим работы элементов цепи, при котором она ведет себя, по отношению к источнику энергии, как чисто активное сопротивление, т.е. напряжение и ток совпадают по фазе.

Р езонанс напряжения:

z₁=R;

z₂=jL=jX_L;

z₃=-j/c=-jX_C;

z=z₁+z₂+z₃=R+jX_L-jX_C=R+j(X_L-X_C);

X_L=X_C – условие резонанса напряжения.

L=1/C;

₀=1/(LC) – резонансная частота.

Сопротивление любого реактивного элемента по резонансной частоте называется характеристическим сопротивлением последовательного колебания контура.

=₀L=1/₀C=(L/C).

Добротностью контура называется отношение характеристического сопротивления контура к его активному сопротивлению:

q=/R.

Замечание:

Резонанс напряжения характеризуется следующим:

1. Ток в режиме резонанса maх: I_рез=U/Z =U/R;

2. Напряжения на реактивных элементах возрастают в q-раз по отношению к напряжению источника питания:

U_L=X_LI_рез;

U_C=X_CI_рез;

U_L=U_C;

U_R+U_L+U_C=I_резR+I_резjX_L+I_рез(-jX_C)=I_резR+I_резj(X_L-X_C)=I_резR; U_L/U=U_C/U=I_рез/RI_рез=/R=q.

3. Реактив. мощность Q_L u Q_C равны между собой, а активная мощность максимальная.

P=I²_резR;

Q=Q_L-Q_C=I²_резX_L-I²_резX_C=I²_рез(X_L-X_C)=0;

Реактив мощность, потребляемая контуром, равна 0.
В екторная диаграмма – совокупность векторов комплексных значений синусоидальных величин.

U_L=U_C;

Q_C=Q_L;

Cos(φ)=1 – коэффициент мощности.
15. Резонанс токов. Векторная диаграмма.

Резонанс токов:

z 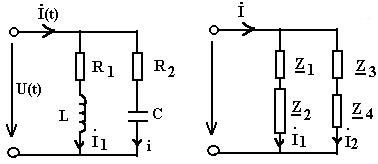₁=R₁;

z₂=jL=jX_L;

z₃=R₃;

Величина обратная контурному сопр-ю наз. комп. проводн.

Y=1/Z=UY=U(g+jb)=Ug+Ujb=

=I_A+jI_P;
Y₁=1/(z₁+z₂)=1/(R₁+jX_L)=(R₁-jX_L)/(R₁²+X_L²)=(R₁/(R₁²+X_L²))–j(X_L/(R₁²+X_L²));

(R₁/(R₁²+X_L²))=g₁ – активная проводимость ветви1.

(jX_L/(R₁²+X_L²))=b_L – индуктивная проводимость контура.

Y₂=1/(z₃+z₄)=1/(R₂-jX_С)=(R₂+jX_С)/(R₂²+X_С²)=(R₂/(R₂²+X_С²))+j(X_С/(R₂²+X_С²));

(R₂/(R₂²+X_С²))=g₂ – активная проводимость ветви 2;

(jX_С/(R₂²+X_С²))=b_C – емкостная проводимость контура;

Y=Y₁+Y₂=g₁-jb_L+g₂+jb_C=g₁+ g₂+j(b_C-b_L);

I=UY=U(g+j(b_C-b_L));

b_C=b_L – условие резонансов токов;

R₁=R₂=0;

b_L=1/X_L=1/L;

b_C=1/X_С=1/(1/С)=С;

b_L=b_C =>1/L=C;

’₀=(1/LC) – резонансная частота ||-го контура без потерь,

=(L/C) – характеристическое сопротивление ||-го контура без потерь,

₀=((²-R₁²)/(²-R₂²)) – резонансная частота ||-го контура.

Резонансной частотой колебательного контура опр-ся не только параметрами реактив. эл-ов вх-х в контур, но и параметрами активных эл-в, т.е. R₁ и R₂. Если R₁=R₂= - резонанс наступает на любых частотах.

Резонанс токов хар-ся след:

1. Полная проводимость контура=активной проводимости, а значит минимальна. Ток в неразветвл. части цепи минимален.

2. Реактивн. состояния токов в ветвях максимальны и противопол. по фазе.

3. Реактивные мощности Q_L и Q_C равны, а их суммарная реактивная мощность контура=0. Q_L=U²b_L; Q_С=U²b_С; Q= Q_L-Q_C= U²(b_L-b_C)=0;
16. Мощность в цепи переменного тока (полная, активная, реактивная, мгновенная).

Мощность в цепи переменного тока.

Мгновенная мощность – это произведение мгновенных значений напряжения и тока.

U(t)=U_msin(t);

i(t)=I_msin(t+);

P(t)=U(t)*i(t)=U_msin(t)*I_msin(t+)=UIcos+UIcos(2t+);

Постоянная составляющая мгновенной мощности характеризует собой необратимые преобразования электрической энергии в другие виды энергии.

Переменная составляющая мгновенной мощности, которая колеблется с частотой в два раза превышающей частоту тока в цепи, а значит за время периода два раза изменяющая свой знак, характеризует собой взаимообмен энергии между приемником и источником энергии. Очевидно, что среднее значение переменной составляющей за период равно 0.

средняя мощность в цепи перемен тока за интервал времени от 0 до :
P – активная мощность, Q – реактивная мощность, ее среднее значение за период=0

P=I_mU_m/2cos=(U_m/2)(I_m/2)cos=IUcos;

U_m/2 – действующее значение напряжения в цепи.

I_m/2 – действующее значение тока.

Активная мощность характеризует мощность, которая безвозвратно превращается в др. виды энергии (преобразовывает в тепловую энергию).

Реактивная мощность(Q) характеризует тот факт, что происходят обратимые преобразования энергии. Максимальное значение переменной составляющей мгновенной мощности за период. Подразделяется на индуктивную и емкостную.

Q=UIsin; P=U_RI=I²R; Q_L=U_LI=I²X_L; Q_C=U_CI=-I²X_C; Q=Q_L-Q_C;

Cosφ – коэффициент мощности, показывает, какая часть потребляемой мощности необратимо образуется в другие виды энергии.

Реактивная мощ-ть катушки индуктивности всегда (+), а конденсатора(-).

S=UI; P=IUcos; Q=UIsin; S=√(P²+Q²);
17. Баланс мощностей в цепи переменного тока. Коэффициент мощности.

Баланс мощностей в цепи перемен. тока.

1. 
   Р_ист=Р_пр=RI²;
   

Активная мощность источников энергии равна в цепи переменного тока сумме активных мощностей приемников электрической энергии.

2. 
   Q_ист=Q_пр=XI²
   

Алгебраическая сумма реактивных мощностей приемников энергии = алгебраической сумме реактивных мощностей источников энергии.
Коэффициент мощности (cos)

1 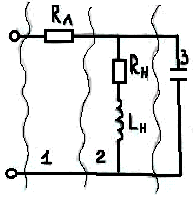– линия передачи энергии,

2 – приемник электрической энергии,

3 – конденсатор реактивной мощности.

Сопротивление R_Н символизирует мощность, которая расходуется безвозвратно, т.е. переходит в другие виды энергии.

R_Л – сопротивление линий передачи энергии.

Большинство потребителей имеет индуктивный хар-р, т.к. необходимо наличие реактивной мощ-ти для создания магнитного поля. В связи с этим напряжение опережает ток на угол . Косинус этого угла и называется коэффициентом мощности.

Коэффициент мощ-ти (cos) – это отношение активной мощности к полной мощности и показывает какая часть электрической энергии необходимо преобразовать в другие виды энергии:

cos=P/S=I_A/I;

По линии передачи эл. эн. кроме активной мощности передается реактивная (индукция) мощность, кот. в течении одного периода колебания заимствуется из источника энергии и затем возвращается ему. Это постоянно перетекающая мощность. Для компенсации реактивной мощности, ||-но c нагрузкой подключают элемент, имеющей ёмкостный хар-р. В результате реактивная мощность, необходимая для создания магнитного поля, заимствуется не по линии передачи энергии, имеющей существенное сопротивление из-за её большой протяжённости, а от источника реактивной мощности, расположенного непосредственно возле приёмника электроэнергии, т.е. практически без потерь. Идеальный случай компенсации, когда cos=1. Если реактивная мощность компенсатора больше реактивной мощности приёмника, то cos<1 и в линии передачи энергии опять-таки будет протекать реактивная (ёмкостная) мощность. Это явление называется перекомпенсация и также нежелательно.
18. Переходные процессы в цепях постоянного тока. Законы коммутации.