Шпоры по электротехнике. 1. Электрическая цепь (ЭЦ), элемент эц, электрическая схема. Источники и приемники электрической энергии

• Название: 1. Электрическая цепь (ЭЦ), элемент эц, электрическая схема. Источники и приемники электрической энергии
• Анкор: Шпоры по электротехнике
• Дата: 26.02.2023
• Размер: 0.69 Mb.
• Имя файла: Shpory_po_elektrotekhnike_1.doc
• Тип: Документы; #955695
• страница: 2 из 4

Переходные процессы в цепи постоянного тока

Любые изменения в электрических цепях можно представить в виде переключения, называемом в общем случае коммутацией. Процессы, возникающие при переходе цепи из одного установленного режима в другой, называются переходными. Возникновение переходных процессов обусловлено наличием в цепи ёмкостных и индуктивных элементов, которые способны накапливать соответственно энергию электрического и магнитного поля.

Законы коммутации:

1. 
   Ток в цепи с индуктивным элементом в начальный момент после коммутации (+0) имеет тоже значение, что и перед коммутацией (-0), т.е. ток через индуктивность не может измениться скачком.
   

i_L(+0)=i_L(-0)=i_L(0); iR+L(di/dt)=E; L(di/dt)→∞.

С 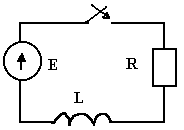качкообразное изменение тока означает, что di/dt=∞, а величина тока, ЭДС и сопротивление конечны, тогда скачкообразное изменение тока через индуктивность противоречит 2-му закону Кирхгофа.

2) Напряжение на емкостном элементе в начальный момент времени после коммутации имеет тоже значение, которое оно имело перед коммутацией, т.е. напряжение на емкостном элементе не может измениться скачком. u_C(+0)= u_C(-0)= u_C(0); iR+ u_C=E; i=C(du_C/dt); CR(du_C/dt)+u_C=E;

Е сли напряжение на ёмкостном элементе изменится скачком, то du_C/dt→∞ и первое значение в формуле также →∞, а поскольку u_C величины конечные, то это привело бы к нарушению 2-го закона Кирх.

i_L(+0)=i_L(-0)=i_L(0) и u_C(+0)=u_C(-0)=u_C(0) – начальные условия переходного процесса.

21. Дифференцирующие и интегрирующие звенья

Интегрирующее звено:

- U_вх+iR+U_C=0;

U_вх=iR+U_C; iR>>U_C;

U_вх=iR;

i=C(dU_C/dt);

i=C(dU_вых/dt);

U_вх=RC(dU_вых/dt);

Звено является интегрирующим, если длительность интервала интегрирования много меньше постоянной времени этого звена. В случае синусоидального напряжения необходимым условием является:

U_R>>U_С; IR>>IX_С; R>>X_С; R>>1/C; CR>>1;

=2/T; 2/TRC>>1; (2/T)τ>>1; 2τ=T;

Дифференцирующее звено: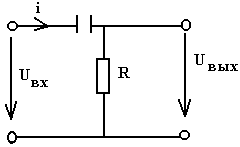

- U_вх+iR+U_C=0;

U_вх=iR+U_C; U_C>>iR;

U_вх=U_C;

U_вых=iR;

i=C(dU_C/dt);

U_вых=Ri=RC(dU_вх/dt)=τ(dU_вх/dt);

Звено является дифференцируемым, если t>>τ; если звено включено в цепь синусоидального тока, то

U_C>>U_R; IX_С>>IR; X_С>>R; 1/C>>R; 1>>R/C;

=2/T; RC=τ; 1>>τ2/T; T>>τ2 – необходимое условие;

22. Трехфазная электрическая цепь. Получение трехфазного тока.

Способы изображения трехфазной симметричной системы ЭДС.

Трехфазные цепи. Трехфазные системы ЭДС.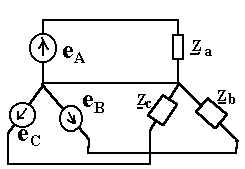



3 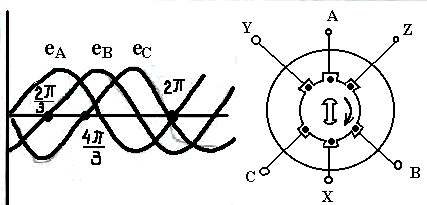-х фазные цепи – это совокупность 3-х однофазных цепей, в кот. действуют синусоидальные ЭДС одной и той же частоты, сдвинутые по фазе на угол 120.

Достоинства: передача электрической энергии на дальние расстояния более выгодно, чем по однофазным цепям. Кроме того, 3-х фазные асинхронные, синхронные, двигательные трансформаторы просты в изготовлении и практичны. В 3-х фазной системе легко получить вращающееся магнитное поле.

е_А=Е_Мsint; е_B=Е_Мsin(t-120);

е_C=Е_Мsin(t+120); E_A=(E_m/2)e^j0=E;

E_B=(E_m/2)e^-j180=Ee^-j180;

E_C=(E_m/2)e^j120=Ee^j120;

П 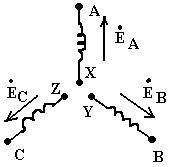ри вращении ротора, создаваемого постоянное магнитное поле с угловой скоростью, в обмотках статора, сдвинутых в пространстве на угол 120, наводятся синусоидальные ЭДС по частоте и амплитуде и сдвинутые на Т/3 относительно друг друга.


23. Способы соединения источников трехфазного переменного тока. Соотношения между фазными и линейными напряжениями.

Способы соединения фаз 3-х фазного источника. Линейные и фазные напряжения и токи.

П 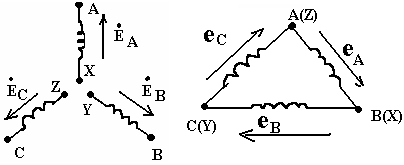ри соед. звездой концы фаз соед-ся в общей т. назыв-ой нейтральной, а начала фаз подключают к приемникам элект-ой энерг. При соед. фаз источн. в треугольн. конец фазы соед-ся с началом предыдущей, а к образовавшимся вершинам треугольн. подключается приемники энергии.

Напр-е м/у началами и концами фаз наз. фазными. Токи протекающие в фазе наз-ся фазными. Провода соед-е ист. энергии и приемники энергии, т.е. провода соед. т. А,а, В,в, С,с, наз-ся линейными. Напр-е м/у линейными проводами наз-ся линейным, токи в этих проводах тоже линейные.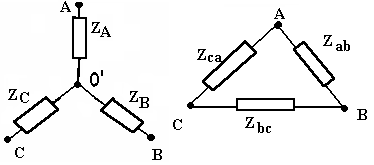



24. Схема соединений «звезда» - «звезда» с нулевым проводом.

Векторная диаграмма. Симметричная и несимметричная нагрузка.

Соед-е звезда-звезда с нулевым проводом.

I 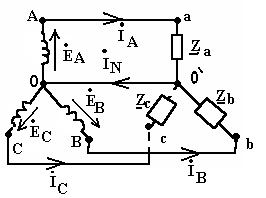_A=I_Ф;

U_A=3U_Ф;

Провод соед-й нейтральные т. Генератора и нагрузки наз-ся нейтральным или нулевым.

I_A=U_A/Z_A; I_B=U_B/Z_B; I_C=U_C/Z_C;

I_A+I_B+I_C=I_N;

Нагрузка наз-ся симметричной если: Z_A=Z_B-Z_C; Во всех 3-х фазах нагрузка одинакова, если нагр-ка симметрична, то ток в нейтральном проводе=0. Расчет сводится к расчету тока в одной фазе.Токи сдвинуты от-но ф.напряжений на тот же угол ф.

Векторная диаграмма:

Симметричная: Несимметричная:

0=I_n=Ia+Ib+Ic I_n=Ia+Ib+Ic

В случае несимметричной нагрузки в нейтральном проводе протекает уравновешивающий ток, благодаря которому остаются неизменному фазные напряжения в независимости от характера нагрузки.

25. Схема соединений «звезда» - «звезда» без нулевого провода.

Векторная диаграмма. Симметричная и несимметричная нагрузка.

Тк в звезда-звезда в нейтр. проводе нет тока. То можно соединять без него.

Теперь проводов не 4, а3.

С 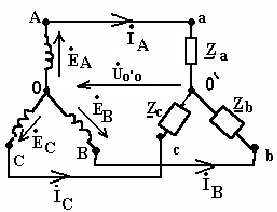имметр.нагр.

Тк. Za=Zb=Zc, расчет ведется на одну фазу
Ia=Ua/Za=Uфe^j0/Zфe^jф=Iфe^-jф U_Л=3U_Ф

Несимм.нагр

Y_A=1/Z_A; Y_В=1/Z_B; Y_C=1/Z_C;

U_0'0=(E_AY_A+E_ВY_В+E_CY_C)/(Y_A+Y_В+Y_C);

Фазные напряжения приемника не равны напряжениям ген.

Из за смещения нейтрали: Ua=UA-UnN……

Токи Ia=YaUa……

Напр-е U_0'0 – т.е. напр-е м/у нейтр-ми т. генер. и нагрузки наз-ся смещением нейтрали. Смещение нейтрали=0, если нагрузка симметрична. Смещение нейтрали отсутствует. В случае симметричной нагрузки U_Л=3U_Ф; т.к. смещ-е нейтрали=0.

U_A – линейное, U_Ф – фазное. U_0'0-смещение нейтрали.

U_а0'=E_A-U_0'0; U_в0'=E_В-U_0'0; U_с0'=E_С-U_0'0;

I_A=U_а0'/Z_A=U_а0'Y_A; I_В=U_в0'/Z_В=U_в0'Y_В; I_С=U_с0'/Z_С=U_с0'Y_С;

U_Л= U_Ф3U_Ф – в случае симметричной нагрузки; U_00' =0

26. Соединения приемников «треугольником». Векторная диаграмма.

Соотношения между линейными и фазными токами при симметричной и

несимметричной нагрузке.