ФИЗИКА. 1. Электрическое поле особая форма
 Скачать 279 Kb.
|
|
ФИЗИКА 1. Электрическое поле — особая форма материи, существующая вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде в электромагнитных волнах. Электрическое поле непосредственно невидимо, но может наблюдаться по его действию и с помощью приборов. Основным действием электрического поля является ускорение тел или частиц, обладающих электрическим зарядом. Электрическое поле можно рассматривать как математическую модель, описывающую значение величины напряженности электрического поля в данной точке пространства. Дуглас Джанколи писал так:"Следует подчеркнуть, что поле не является некой разновидностью вещества; правильнее сказать, это чрезвычайно полезная концепция… Вопрос о «реальности» и существовании электрического поля на самом деле — это философский, скорее даже метафизический вопрос. В физике представление о поле оказалось чрезвычайно полезным — это одно из величайших достижений человеческого разума". Электрическое поле является одной из составляющих единого электромагнитного поля и проявлением электромагнитного взаимодействия. 2. Электроемкость характеризует способность проводников или системы из нескольких проводников накапливать электрические заряды, а следовательно, и электроэнергию, которая в дальнейшем может быть использована, например, при фотосъемке (вспышка) и т.д. Различают электроемкость уединенного проводника, системы проводников (в частности, конденсаторов). Уединенным называется проводник, расположенный вдали от других заряженных и незаряженных тел так, что они не оказывают на этот проводник никакого влияния. Электроемкость уединенного проводника — физическая величина, равная отношению электрического заряда уединенного проводника к его потенциалу  В СИ единицей электроемкости является фарад (Ф). 1 Ф — это электроемкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл. Поскольку 1 Ф очень большая единица емкости, применяют дольные единицы: 1 пФ (пикофарад) = 10-12 Ф, 1 нФ (нанофарад) = 10-9 Ф, 1 мкФ (микрофарад) = 10-6 Ф и т.д. 3. Как и любая система заряженных тел, конденсатор обладает энергией. Вычислить энергию заряженного плоского конденсатора с однородным полем внутри него несложно. Энергия заряженного конденсатора. Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта работа равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, содержащую лампу накаливания, рассчитанную на напряжение в несколько вольт (рис.14.37). При разрядке конденсатора лампа вспыхивает. Энергия конденсатора превращается в тепло и энергию света. 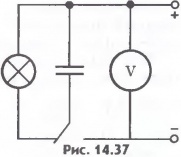 Выведем формулу для энергии плоского конденсатора. Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е -напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины (рис.14.38). Согласно формуле (14.14) для потенциальной энергии заряда в однородном поле энергия конденсатора равна: 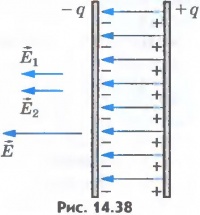  где q - заряд конденсатора, а d - расстояние между пластинами. Так как Ed=U, где U - разность потенциалов между обкладками конденсатора, то его энергия равна:  Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную. Заменив в формуле (14.25) разность потенциалов или заряд с помощью выражения (14.22) для электроемкости конденсатора, получим:  Можно доказать, что эти формулы справедливы для любого конденсатора, а не только для плоского. 4. Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1]. По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил  , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре  ЭДС будет равна: где  — элемент контура.ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого́ источника равна нулю. 5. Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда. Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси. В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов. 6. Различают полупроводниковые материалы n-типа и p-типа. 7.Полупроводники n-типа   Полупроводник n-типа Термин «n-тип» происходит от слова «negative», обозначающего отрицательный заряд основных носителей. Этот вид полупроводников имеет примесную природу. В четырёхвалентный полупроводник (например, кремний) добавляют примесь пятивалентного полупроводника (например, мышьяка). В процессе взаимодействия каждый атом примеси вступает в ковалентную связь с атомами кремния. Однако для пятого электрона атома мышьяка нет места в насыщенных валентных связях, и он переходит на дальнюю электронную оболочку. В этой электронной оболочке для отрыва электрона от атома нужно меньшее количество энергии. Электрон отрывается и превращается в свободный электрон. В данном случае перенос заряда осуществляется электроном, а не дыркой, то есть данный вид полупроводников проводит электрический ток подобно металлам. Примеси, которые добавляют в полупроводники, вследствие чего они превращаются в полупроводники n-типа, называются донорными примесями. Проводимость полупроводников n-типа приблизительно равна: σ≈qN n μ n Полупроводники р-типа  Полупроводник p-типа Термин «p-тип» происходит от слова «positive», обозначающего положительный заряд основных носителей. Этот вид полупроводников, кроме примесной основы, характеризуется дырочной природой проводимости. В четырёхвалентный полупроводник (например, в кремний) добавляют небольшое количество атомов трехвалентного элемента (например, индия). Каждый атом примеси устанавливает ковалентную связь с тремя соседними атомами кремния. Для установки связи с четвёртым атомом кремния у атома индия нет валентного электрона, поэтому он захватывает валентный электрон из ковалентной связи между соседними атомами кремния и становится отрицательно заряженным ионом, вследствие чего образуется дырка. Примеси, которые добавляют в этом случае, называются акцепторными примесями. Проводимость полупроводников p-типа приблизительно равна: σ≈qN p μ p 8. Опыт Эрстеда — классический опыт, проведённый в 1820 году Эрстедом и являющийся первым экспериментальным доказательством воздействия электрических токов на магниты Ганс Христиан Эрстед помещал над магнитной стрелкой прямолинейный металлический проводник, направленный параллельно стрелке. При пропускании через проводник электрического тока стрелка поворачивалась почти перпендикулярно проводнику. При изменении направления тока стрелка разворачивалась на 180°. Аналогичный разворот наблюдался, если провод переносился на другую сторону, располагаясь не над, а под стрелкой. Принято считать, что это открытие было совершенно случайно: профессор Эрстед демонстрировал студентам опыт по тепловому воздействию электрического тока, при этом на экспериментальном столе находилась также и магнитная стрелка. Один из студентов обратил внимание профессора на то, что в момент замыкания электрической цепи стрелка немного отклонялась. Позднее Эрстед повторил опыт с более мощными батареями, усилив тем самым эффект. При этом сам он в своих поздних работах опровергал случайный характер открытия: «Все присутствующие в аудитории — свидетели того, что я заранее объявил о результате эксперимента. Открытие, таким образом, не было случайностью…» 9. Линией магнитной индукции (магнитной линией) называется такая линия, касательная к которой в любой точке совпадает с направлением вектора магнитной индукции. 10. Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен  и не зависит[2] от амплитуды колебаний и массы маятника. Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы. При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной. 11 Волны - колебания, распространяющиеся в пространстве с течением времени. Волновой процесс- процесс распространения колебаний в сплошной среде. Упругие волны- механические возмущения, распространяющиеся в упругой среде. При распространении волны частицы среды не перемещ-ся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной передаётся лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн независимо от природы явл-ся перенос энергии без переноса вещества. Различают механические волны, электромагнитные волны и волны на поверхности жидкости. В твёрдых телах, внутри жидкости и газа волны возникают благодаря силам упругости, а на поверхности жидкости - благодаря силе тяжести и силе поверхностного натяжения. Упругие волны бывают поперечные, если колебания совершаются в направлении, перпендикулярном распространению волны. Они возникают в твёрдых телах и на поверхности жидкости благодаря деформации сдвига и продольные если колебания совершаются в направлении распространения волны. Они возникают в твёрдых телах, внутри жидкости и газах благодаря деформации растяжения и сжатия. Длина волны ? (м) - расстояние между ближайшими точками, колеблющимися в одной фазе. За один период волна проходит расстояние, равное одной длине волны. За 1 период волна проходит расстояние, равное одной длине волны. Интенсивность волны - энергия, переносимая через единичную площадь за единицу времени: I=W/St (Дж/м/с). 12. Корпускуля́рно-волново́й дуали́зм (или Ква́нтово-волново́й дуали́зм) — принцип, согласно которому любой физический объект может быть описан как с использованием математического аппарата, основанного на волновых уравнениях, так и с помощью формализма, основанного на представлении об объекте как частице или системе частиц. В частности, волновое уравнение Шрёдингера не накладывает ограничений на массу описываемых им частиц, и следовательно, любой частице, как микро-, так и макро-, может быть поставлена в соответствие волна де Бройля. В этом смысле любой объект может проявлять как волновые, так и корпускулярные свойства[1]. Идея о корпускулярно-волновом дуализме была использована при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. В соответствии с теоремой Эренфеста квантовые аналоги системы канонических уравнений Гамильтона для макрочастиц приводят к обычным уравнениям классической механики. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантованных полей в квантовой теории поля. Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных волн. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла[2]. Характер решаемой задачи диктует выбор используемого подхода: корпускулярного (фотоэффект, эффект Комптона), волнового или термодинамического[3]. Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей, что наглядно показал эксперимент, проведённый французскими физиками Гранжье, Роже и Аспэ в 1986 году[4]. Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон). Сейчас концепция корпускулярно-волнового дуализма представляет лишь исторический интерес, так как, во-первых, некорректно сравнивать и/или противопоставлять материальный объект (электромагнитное излучение, например) и способ его описания (корпускулярный или волновой); и, во-вторых, число способов описания материального объекта может быть больше двух (корпускулярный, волновой, термодинамический, …), так что сам термин «дуализм» становится неверным. На момент своего возникновения концепция корпускулярно-волнового дуализма служила способом интерпретировать поведение квантовых объектов, подбирая аналогии из классической физики. На деле квантовые объекты не являются ни классическими волнами, ни классическими частицами, приобретая свойства первых или вторых лишь в некотором приближении. Методологически более корректной является формулировка квантовой теории через интегралы по траекториям (пропагаторная), свободная от использования классических понятий. 13. Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения). Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания Резонансная частота контура определяется так называемой формулой Томсона:  Пусть конденсатор ёмкостью C заряжен до напряжения  . Энергия, запасённая в конденсаторе составляет  Параллельный колебательный контур  Осциллограмма LC контура во время замыкания заряженного конденсатора на катушку индуктивности. С - 240нФ(заряженный) L - 360нГн F0 ≈ 542кГц При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток  , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора  . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна , где — индуктивность катушки,  — максимальное значение тока.После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения  .В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре. В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром. Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности. 14. Радиолока́ция — область науки и техники, объединяющая методы и средства локации (обнаружения и измерения координат) и определения свойств различных объектов с помощью радиоволн. Близким и отчасти перекрывающимся термином является радионавигация, однако в радионавигации более активную роль играет объект, координаты которого измеряются, чаще всего это определение собственных координат. Основное техническое приспособление радиолокации — радиолокационная станция (РЛС, англ. radar). Различают активную, полуактивную, активную с пассивным ответом и пассивную радиолокацию. Радиолокаторы различаются по используемому диапазону радиоволн, по виду зондирующего сигнала, числу применяемых каналов, числу и виду измеряемых координат, месту установки РЛС. Выделяют два вида радиолокации: Пассивная радиолокация основана на приёме собственного излучения объекта При активной радиолокации радар излучает свой собственный зондирующий импульс и принимает его отражённым от цели. В зависимости от параметров принятого сигнала определяются характеристики цели. Активная радиолокация бывает двух видов:  Активная радиолокация с пассивным ответом С активным ответом — на объекте предполагается наличие радиопередатчика (ответчика), который излучает радиоволны в ответ на принятый сигнал. Активный ответ применяется для опознавания объектов (свой-чужой), дистанционного управления, а также для получения от них дополнительной информации (например, количество топлива, тип объекта и т. д.). С пассивным ответом — запросный сигнал отражается от объекта и воспринимается в пункте приёма как ответный. Для просмотра окружающего пространства РЛС использует различные способы обзора за счёт перемещения направленного луча антенны РЛС: круговой секторный обзор по винтовой линии конический по спирали «V» обзор линейный (самолёты ДРЛО типа Ан-71 и А-50 (Россия-Украина) или американские с системой Авакс) В соответствии с видом излучения РЛС делятся на РЛС непрерывного излучения Импульсные РЛС 15.Ядерная модель атома В начале 20 века в результате изучения катодных лучей были обнаружены отрицательные частицы – электроны с зарядом 1,6.10‾19 Кл, массой 9,11.10‾31 кг, открыто рентгеновское электромагнитное излучение. Обобщив эти открытия, Дж.Томсон в 1897 году предложил свою модель атома – это положительно заряженная сфера, в которую вкраплены отрицательные электроны (подобно изюму в пудинге). Если эта модель верна, тогда металлическая фольга – это пленка положительного электричества, содержащая электроны и поток α- частиц должен легко проникать через нее, не меняя направление. В 1909 г. сотрудники англ. ученого Э. Резерфорда это проверили. 1 из 100000 α - частиц при прохождении через золотую фольгу рассеивались на большие углы и даже поворачивали обратно. Анализируя результаты эксперимента, Резерфорд сделал вывод, что масса и заряд атома сконцентрированы в малой части объема, называемой ядром. Отклоняются те α - частицы, которые сталкиваются с ядрами. Большинство же α - частиц проходит через пространство между ядрами. Модель строения атома, предложенная Э. Резерфордом, напоминала солнечную систему. Ее называют планетарной моделью. Согласно ей, в центре атома находится положительное ядро, в котором сосредоточена вся масса атома. Вокруг ядра по круговым орбитам движутся электроны. Заряд ядра и число электронов одинаковы, т.е. атом нейтральная частица. |