телекоммуникации. 1. элементы теории передачи информации информация, сообщение, сигнал Понятие информация
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
|
При передаче непрерывных сообщений отличие принятого сообщения b*(t) от переданного b(t) носит также непрерывный характер: Для оценки достоверности передачи сообщений в данном случае обычно используют средний квадрат ошибки или относительный средний квадрат ошибки где усреднение производится по всем реализациям сообщений b(t) и их оценкам b*(t), Возможны и другие показатели достоверности, как, например, показатель максимальной абсолютной ошибки εmax=max׀ε(t) ׀. Под помехоустойчивостью понимают способность системы противостоять вредному действию помех на передачу сообщений. Количественно помехоустойчивость телекоммуникационных систем можно характеризовать вероятностью ошибки pош при заданном отношении средних мощностей сигнала и помехи в полосе частот занимаемой сигналом, или требуемым отношением средних мощностей сигнала и помехи на входе приемника системы, при котором обеспечивается заданная вероятность ошибки pош. Еще одна важная характеристика – скорость передачи информации – будет введена ниже. 1.4. Информационные характеристики источника дискретных сообщений и канала связи 1.4.1. Количественная оценка информации Для сравнения различных систем телекоммуникаций необходимо ввести количественную меру, позволяющую оценивать объем информации, содержащейся в сообщении. Строгие методы количественного определения информации были предложены К.Шенноном в 1948 г. и привели к построению теории информации, являющейся основой теории связи, информатики и ряда смежных отраслей науки и техники. 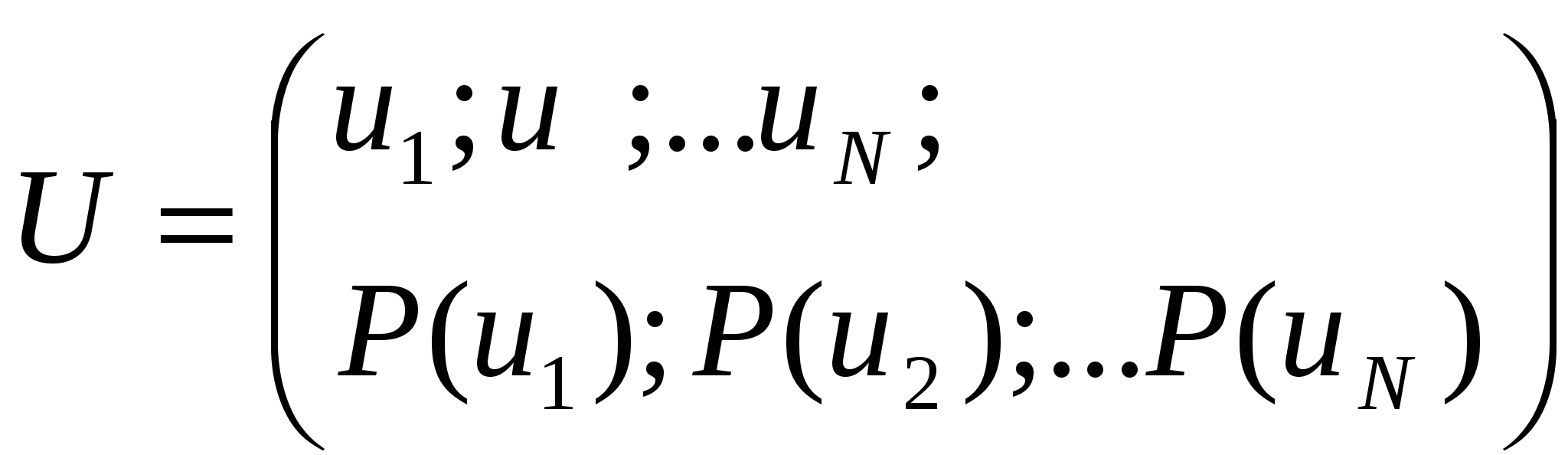 Рассмотрим основные идеи этой теории применительно к дискретному источнику сообщений, который в каждый момент времени случайным образом может принимать одно из конечного множества возможных состояний. Каждому состоянию источника сообщений ставится в соответствие условное обозначение в виде знака (в частности буквы) из алфавита данного источника u1, u2, u3 ..., uN. Одни состояния выбираются источником сообщений чаще, другие реже. Поэтому наряду с множеством состояний целесообразно задать вероятность их появления: Или: 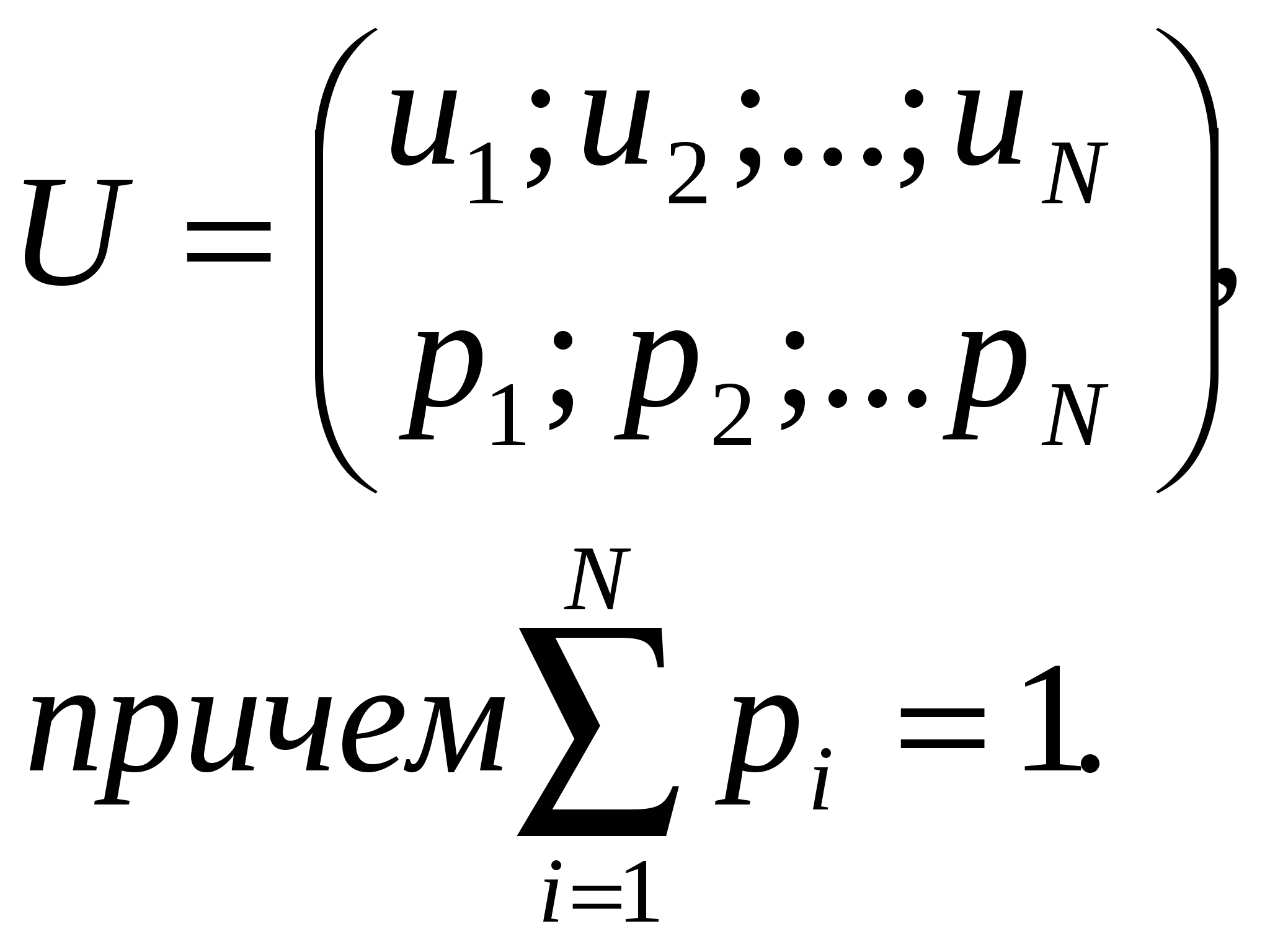 Совокупность состояний и вероятностей их получения называется ансамблем U. Перед тем как ввести определение количества информации, сформулируем условия, которым должна удовлетворять эта величина:
I(ui , uk) = I(ui )+ I(uk ); (1.3)
Итак, для определения количества информации в некотором сообщении ui из ансамбля U необходимо основываться только на таком параметре, который характеризует в самом общем виде это сообщение. Таким параметром, очевидно, является вероятность pi появления данного сообщения на выходе источника. Дальнейшее уточнение искомого определения не составит труда, если принять во внимание первые два из перечисленных выше условий. Пусть uiи uk - два независимых события. Вероятность того, что оба этих сообщения появятся на выходе источника одно за другим Р(ui , uk) = Р(ui )*Р(uk ), (1.4) а количество информации в этих сообщениях должно удовлетворять условию (1.3). Следовательно, необходимо найти функцию, обладающую свойством, что при перемножении двух аргументов значения функции складываются. Единственная такая функция – это логарифмическая функция I(u)=klogP(u), где k- постоянный коэффициент. Заметим, что при таком определении количества информации выполняется и второе требование - при P(u)=1 I(u)=0. Основание логарифма не имеет принципиального значения и определяет только масштаб функции. Так как информационная техника широко использует элементы, имеющие два устойчивых состояния, то обычно основание логарифма выбирают равным 2. В дальнейшем обозначение log, если основание не оговаривается особо, будет означать двоичный логарифм. Чтобы количество информации I(u) было неотрицательной величиной, выбирают k=1. Поэтому I(u)= logP(u). Если источник передает последовательность зависимых между собой сообщений, то получение предшествующих сообщений может изменить вероятность последующего, а следовательно, и количество информации в нем. Оно должно определяться по условной вероятности передачи данного сообщения uk при известных предшествовавших сообщениях uk-1,uk-2,…: I(uk uk-1,uk-2,…)= logP(ukuk-1,uk-2,…).(1.5) Введенное выше определение характеризует количество информации, содержащееся в одном сообщении из ансамбля U. При этом I(u) является случайной величиной, зависящей от того, какое состояние источника в действительности реализуется. Для характеристики всего ансамбля (или источника) используется математическое ожидание количества информации, называемое энтропией и показывающее, какое количество информации в среднем содержится в одном сообщении данного источника H(U)=MlogP(u) . (1.6) Для источника независимых сообщений выражение (1.6.) можно представить в виде H(U)= P(ui)logP(ui), i=1, …, N. (1.7) Пример 1. Рассмотрим случай, когда алфавит состоит из двух знаков, появляющихся на выходе источника сообщений независимо друг от друга. Обозначим P(u1)=P. Соответственно P(u2)=1-P. Тогда на основании (1.7.) имеем H(U)= PlogP(1P)log(1P). (1.8) Если события u1 и u2 являются равновероятными, то P=1/2. Подставив это значение в (1.8.), получим H(U)=1. В общем виде зависимость H(U) от Р показана на рис. 1.4. 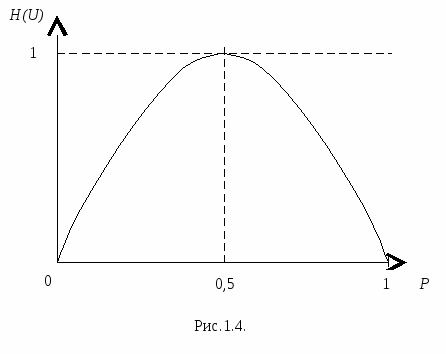 Количество информации, содержащееся в среднем в одном символе алфавита, состоящего из двух знаков, которые появляются на выходе источника сообщений независимо друг от друга и равновероятно, получило название "1 бит информации" или просто 1 бит. Случай, когда алфавит источника сообщений состоит всего из двух знаков, широко распространен на практике. В качестве примера можно привести цифровые системы, использующие алфавит, состоящий из знаков 0 и 1. Чем больше энтропия источника, тем больше степень неожиданности передаваемых им сообщений в среднем, т.е. тем более неопределенным является ожидаемое сообщение. Поэтому энтропию часто называют мерой неопределенности сообщений. При этом имеется в виду неопределенность, существующая до того, как сообщение передано. После приема сообщения, если оно передано верно, всякая неопределенность устраняется. Это позволяет трактовать количество информации как меру уменьшения неопределенности. 1.4.2. Свойства энтропии источника дискретных сообщений Перечислим основные свойства энтропии:
H(U)logN, (1.8) причем равенство имеет место только тогда, когда все сообщения передаются равновероятно и независимо (P(ui)=1/N; i=1, …, N). Для доказательства последнего свойства воспользуемся неравенством lnw≤ (w-1). (1.9) Рассмотрим разность функций, стоящих в левой и правой частях неравенства (1.8). Путем несложных преобразований ее можно представить в виде: H(U)- logN= Pi log(1/Pi) - Pi logN= Pi log(1/NPi), (1.10) причем суммирование ведется по i=1, …, N. Чтобы воспользоваться неравенством (1.9), перейдем в последнем выражении к натуральному основанию логарифма: H(U)- logN= Pi log(1/NPi)= log e Pi ln(1/NPi). (1.11) Используя (1.9), преобразуем выражение (1.11). Получим: H(U)- logN= log e Pi ln(1/NPi) ≤ log e Pi[1/NPi-1]= =loge (1/N-Pi)=0. (1.12) Знак равенства в (1.8) имеет место тогда, когда в неравенстве (1.9) w=1. Так как в нашем случае w=1/NPi, то условие w=1 эквивалентно Pi=1/N; i=1, …, N. То есть, H(U)= logN в случае, когда все элементы алфавита появляются на выходе источника равновероятно. Свойство (1.8) доказано. Анализируя свойство (1.8), можно прийти к выводу, что чем больше объем алфавита источника дискретных сообщений, тем большее количество информации содержится в среднем в одном символе этого алфавита (при условии, что все элементы алфавита появляются на выходе источника равновероятно). Казалось бы, рассмотренный выше алфавит {0,1}, который широко применяется на практике, следует безоговорочно заменить алфавитами с N»2. Однако следует иметь ввиду, что в реальных условиях различение сигналов, которые могут принимать количество значений N»2, осуществить на фоне помех гораздо сложнее, чем в случае, когда сигналы могут принимать только два значения – 0 и 1. Пример 2. В теории информации доказывается, что энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений при том же объеме алфавита и тех же безусловных вероятностях сообщений. Пусть, например, источник выдает последовательность букв из алфавита объемом N=32. Если буквы выбираются равновероятно и независимо друг от друга, то энтропия источника H(U)= log32=5 [бит]. Однако смысловое содержание такой последовательности букв вряд ли удовлетворит получателя сообщения. Если буквы передаются не хаотически, а составляют связный текст, например, на русском языке, то они оказываются неравновероятными и, главное, зависимыми (так, после гласных не может появиться «ь»; мала вероятность появления 3 гласных или согласных подряд и т.д.). В качестве примера приведем относительные частоты использования некоторых букв русского алфавита в текстах ( в порядке убывания) [4]: «о» - 0,090; «е», «ё» - 0,072 «а», «и» - 0,062 «н», «т» - 0,053 ………………… «ц» - 0,004 «щ», «э» - 0,003 «ф» - 0,002. Как видно из этих данных, различие в частоте появления букв в текстах достигает 45 раз! Если рассматривать ансамбль текстов русской художественной прозы, то энтропия оказывается меньше 1,5 бит на букву. Еще меньше, около 1 бит на букву, энтропия ансамбля поэтических произведений, так как в них имеются дополнительные вероятностные связи, обусловленные ритмом и рифмами [3]. 1.4.3. Избыточность сообщений Рассмотрим ансамбль U, состоящий из N различных символов:u1,u2,…, uN. Энтропия такого дискретного источника достигает максимального значения Hmax(U) = logN, если символы статистически независимы и равновероятны. На практике может оказаться так, что символы, образующие алфавит, нельзя рассматривать как независимые и равновероятные, поэтому для такого источника H(U)<Hmax(U). Предположим, на выходе такого источника появилось сообщение, состоящее из n символов.. Количество информации, содержащееся в нем I=nH(U). (1.13) При использовании алфавита с максимальной энтропией для передачи такого же количества информации потребовалось бы меньшее число символов I=nmin Hmax(U). (1.14) Приравнивая (1.13) и (1.14), находим где µ=H(U)/Hmax(U) <1 – коэффициент, характеризующий допустимую степень сжатия сообщений. Величина χ=1-µ называется избыточностью источника. Последствия от наличия избыточности неоднозначные. С одной стороны, избыточные сообщения требуют дополнительных затрат на передачу (например, увеличивается длительность передачи). С другой стороны, наличие избыточности способствует повышению помехоустойчивости сообщений, подчиняющихся априорно известным условиям (ограничениям), т.к. можно обнаружить и исправить ошибки, приводящие к нарушению этих ограничений. Для сокращения избыточности на практике применяется кодирование источника дискретных сообщений, заключающееся в преобразовании исходного дискретного сообщения по определенному правилу в последовательность кодовых символов, удовлетворяющую требованиям равновероятности и статистической независимости. Устройство, осуществляющее указанную операцию, называется кодером источника. В случае его использования, оно размещается в структурной схеме, приведенной на рис. 1.2, между источником сообщений и передающим устройством. Соответственно, на приемной стороне на выходе приемного устройства необходимо добавить устройство, которое будет осуществлять обратную операцию перед тем, как сообщение поступит получателю. Такое устройство называется декодером. 1.5. Скорость передачи информации по дискретному каналу. Пропускная способность Наряду с введенными в разделе 1.3 такими характеристиками, как достоверность и помехоустойчивость, при оценке эффективности систем связи используется ряд других характеристик, рассмотренных ниже. Технической скоростью Vт называется число элементарных сигналов (символов), передаваемых по каналу в единицу времени. Она зависит от свойств линии связи и быстродействия аппаратуры канала. С учетом возможных различий в длительностях символов Vт =1/τср, |
