вм. СРС ВМ. 1 Елементи теорії матриць

• Название: 1 Елементи теорії матриць
• Дата: 03.06.2022
• Размер: 188.53 Kb.
• Имя файла: СРС ВМ.docx
• Тип: Документы; #567463

Тема 1 Елементи теорії матриць

19 Утворення оберненої матриці

Знаходження оберненої матриці є важливою складовою в розділі лінійної алгебри. З допомогою таких матриць, якщо вони існують, можна швидко знайти розв'язок системи лінійних рівнянь або обчислити матричне рівняння A*X=B.
Матриця A^-1 називається оберненою до матриці A, якщо виконуються наступні рівності

Якщо визначник матриці A відмінний від нуля, то матрицю називають неособливою або невиродженою. Для того, щоб матриця мала обернену необхідно і достатньо, щоб вона була невиродженою.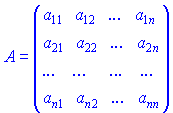



потрібно знайти обернену до неї. Для цього потрібно виконати наступні дії:

1. Знайти визначник матриці  . Якщо він не рівний нулю то виконуємо наступні дії. В іншому випадку дана матриця вироджена і для неї не існує оберненої.

2. Знайти алгебраїчні доповнення елементів матриці A. Вони рівні мінорам, помноженим на (-1)^i+j в степені суми рядка і стовпця, для якого шукаємо.

3. Скласти матрицю з алгебраїчних доповнень елементів матриці A та протранспонувати її. Ця матриця називається приєднаною або союзною і позначається "А з хвиькою"  .

4Поділити приєднану матрицю на детермінант  . Отримана матриця буде оберненою та задовільнятиме властивостям, які викладені на початку статті.

Теорема(необхідна та достатня умова існування оберненої матриці). Обернена до матриці А матриця  існує, причому єдина тоді й тільки тоді, коли матриця А є невиродженою.

Для знаходження обернених до матриць вищих порядків використовується інший метод – метод елементарних перетворень.

Алгоритм методу елементарних перетворень полягає в наступному: справа від матриці А дописують одиничну матрицю такого ж порядку, шляхом елементарних перетворень над рядками матриці А її намагаються звести до одиничної, ті ж перетворення в тому самому порядку здійснюються над відповідними рядками одиничної матриці. Як тільки матриця А перетвориться на одиничну, на місці одиничної матриці буде знаходитись обернена матриця 

При використанні методу елементарних перетворень не потрібно обчислювати визначник матриці А, тому з’ясувати, чи існує обернена до неї можна лише під час реалізації методу, а саме: якщо на певному кроці перетворень у матриці А виникне нульовий рядок, то вона є виродженою і оберненої не має. Інакше обернена існує, причому єдина.

Тема 2 Загальна теорія систем лінійних рівнянь

20 Розв'язування систем лінійних рівннянь способом оберненої матриці

Маричний метод обчислення СЛАР не такий поширений як метод Крамера, однак він присутній в авчальній програмі з лінійної алгебри і його вивчають як один із способів розв'язання системи рівнянь.
Нехай маємо систему N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими x₁, x₂,..., x_N.,коефіцієнтами при яких є елементи матриці A(a_ij), а вільними членами є числа b₁, b₂,..., b_N.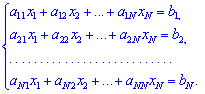



Позначимо через X – матрицю-стовпець невідомих, через B– матрицю-стовпець вільних членів. Тоді попередню систему рівнянь можна записати у вигляді матричного рівняння:
A*X=B
Якщо квадратна матриця A має відмінний від нуля визначник  , то для неї існує обернена A^-1. Помноживши зліва в цьому рівнянні на A^-1, одержимо

Враховуючи, що добуток оберненої матриці на саму матрицю дає одиничну  , а також формулу  , одержимо матричний розв'язок системи
X=A^-1*B
Знаходження матричного розв'язку називається матричним способом розв'язування системи лінійних алгебраїчних рівнянь

21 Метод Гауса

Метод Гаусса-послідовне виключення невідомих. Цей метод використовується для вирішення квадратних систем лінійних алгебраїчних рівнянь. Хоча рівняння за допомогою методу Гаусса вирішуються легко, але все ж студенти часто не можуть знайти правильне рішення, так як плутаються в знаках (плюси і мінуси).

Тому під час вирішення СЛАУ необхідно бути гранично уважним і тільки тоді можна легко, швидко і правильно вирішити навіть найскладніше рівняння. У систем лінійних алгебраїчних рівнянь є кілька переваг: рівняння не обов'язково заздалегідь на спільність; можна вирішувати такі системи рівнянь, в яких число рівнянь не збігається з кількістю невідомих змінних або визначник основної матриці дорівнює нулю; є можливість за допомогою методу Гауса приводити до результату при порівняно невеликій кількості обчислювальних операцій.

СЛАУ в залежності від її елементів може мати: Одне рішення; багато рішень; зовсім не мати рішень. У перших двох випадках СЛАУ називається сумісною, а в третьому випадку – несумісна. Якщо система має одне рішення, вона називається визначеною, а якщо рішень більше одного, тоді система називається невизначеною. Метод Крамера і матричний спосіб не підходять для вирішення рівнянь, якщо система має нескінченну безліч рішень. Ось тому нам і потрібен метод Гаусса, який допоможе нам в будь-якому випадку знайти правильне рішення. До елементарних перетворень відносяться: зміна місць рівнянь системи; почленное множення обох частин на одне з рівнянь на деяке число, так, щоб коефіцієнти при першій змінній в двох рівняннях були протилежними числами; додавання до обох частин одного з рівнянь певних частин іншого рівняння.

Отже, коли ми знаємо основні правила і позначення, можна приступати до вирішення. Тепер розглянемо, як вирішуються системи методом Гауса на простому прикладі: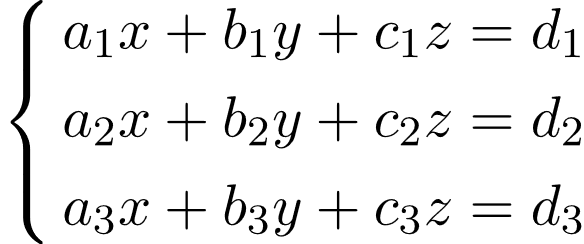



де а, в, с – задані коефіцієнти, d – задані вільні члени, x, y, z – невідомі. Коефіцієнти і вільні члени рівняння можна називати його елементами. Якщо d_1 = d_2 = d_3 = 0, тоді система лінійних алгебраїчних рівнянь називається однорідною, в іншому випадку – неоднорідною. Множини x_0, y_0, z_0 називаються рішенням СЛАУ, якщо при підстановці x=x_0, y=y_0, z=z_0 в СЛАУ отримаємо Числові тотожності.
22 Однорідна система лінійних алгербраїчних рівнянь

Система називається однорідною якщо всі її вільні члени рівні нулю, інакше – система називається неоднорідною. (Однорідна, коли всі доданки однакового степеня.)

Однорідна система має завжди хоча б один розв’язок – нульовий (0;0;…0).

Нехай однорідна система квадратна. Якщо  - один розв’язок (тільки нульовий).

Якщо  - розв’язків безліч.

Властивості розв’язків однорідної системи.
1) якщо  - розв’язки системи,

то і їх сума  - теж розв’язок.

2) якщо - розв’язок системи, k- будь-яке число, то  - теж розв’язок.

Система m лінійних рівнянь з n невідомими називається однорідною якщо всі вільні члени b₁=b₂=...=b_m=0 рівні нулю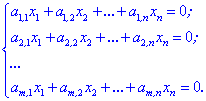



Нульовий розв'язок
x₁=0;x₂=0; ...x_n=0
завжди задовольняє однорідну систему рівнянь. Ненульовий розв'язок (якщо він існує) знаходять методом Гауса. Якщо кількість рівнянь і невідомих однакові m=n і головний визначник рівний нулеві   то однорідна система має безліч розв'язків. Кількість залежних розв'язків рівна рангу системи лінійних рівнянь r(A), решта приймають будь-які значення.
Найчастіше на практичних заняттях зустрічаються системи двох однорідних рівнянь з трьома невідомими та трьох з трьома.
Нехай маємо перший випадок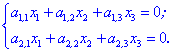



Якщо для деякої множини об’єктів V виконуються такі властивості:

x є V, y є V=> x + y є V; x є V, k є ℝ => kx є V (замкнутість множини V відносно додавання та множення на число). Також виконуються властивості:
перестановочна (комутативність): x+y=y+x;
розподільча (асоціативність): (x + y) + z = x + (y + z);

існує єдиний нульовий елемент 0 є V, такий що 0+х=х для будь-якого х є V;

для кожного елемента х є V існує єдиний протилежний вектор –х, такий що х+(-х)=0;

1×х=х; (km)x=k(mx)

дистрибутивна: k(x + y) = kx +ky, (k+m)x=kx+mx (x,y,z є V, k, m є ℝ).

Тоді множина V- називається лінійним простором (над полем дійсних чисел).

Отже, множина розв’язків однорідної СЛАР є лінійним простором.

Означення. Базис (синонім – основа).

Базисом чи фундаментальною сукупністю елементів лінійного простору V- називається така сукупність його об’єктів через які о д н о з н а ч н о можна виразити будь-який об’єкт лінійного простору з допомогою дій додавання та множення на число.

Вправа. Довести, що елементи базису лінійно незалежні. (Тому що нульовий елемент теж повинен отримуватися єдиним способом, тобто тільки коли всі коефіцієнти  .

Тема 3 Лінії на площині

23 Загальне рівння прямої.Взаємне розміщення прямих.Загальне рівняння площини та його окремі випадки.

Будь-яку пряму на площині можна задати рівнянням прямої першого ступеня вигляду

A x + B y + C = 0

Де A і B не можуть одночасно дорівнювати нулю.

Рівняння прямо Однорідна система лінійних алгербраїчних рівнянь

Система називається однорідною якщо всі її вільні члени рівні нулю, інакше – система називається неоднорідною. (Однорідна, коли всі доданки однакового степеня.)

Однорідна система має завжди хоча б один розв’язок – нульовий (0;0;…0).

Нехай однорідна система квадратна. Якщо  - один розв’язок (тільки нульовий).

Якщо  - розв’язків безліч.

Властивості розв’язків однорідної системи.
1) якщо  - розв’язки системи,

то і їх сума  - теж розв’язок.

2) якщо - розв’язок системи, k- будь-яке число, то  - теж розв’язок.

Система m лінійних рівнянь з n невідомими називається однорідною якщо всі вільні члени b₁=b₂=...=b_m=0 рівні нулю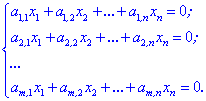



Нульовий розв'язок
x₁=0;x₂=0; ...x_n=0
завжди задовольняє однорідну систему рівнянь. Ненульовий розв'язок (якщо він існує) знаходять методом Гауса. Якщо кількість рівнянь і невідомих однакові m=n і головний визначник рівний нулеві   то однорідна система має безліч розв'язків. Кількість залежних розв'язків рівна рангу системи лінійних рівнянь r(A), решта приймають будь-які значення.
Найчастіше на практичних заняттях зустрічаються системи двох однорідних рівнянь з трьома невідомими та трьох з трьома.
Нехай маємо перший випадок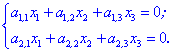



Якщо для деякої множини об’єктів V виконуються такі властивості:

x є V, y є V=> x + y є V; x є V, k є ℝ => kx є V (замкнутість множини V відносно додавання та множення на число). Також виконуються властивості:
перестановочна (комутативність): x+y=y+x;
розподільча (асоціативність): (x + y) + z = x + (y + z);

існує єдиний нульовий елемент 0 є V, такий що 0+х=х для будь-якого х є V;

для кожного елемента х є V існує єдиний протилежний вектор –х, такий що х+(-х)=0;

1×х=х; (km)x=k(mx)

дистрибутивна: k(x + y) = kx +ky, (k+m)x=kx+mx (x,y,z є V, k, m є ℝ).

Тоді множина V- називається лінійним простором (над полем дійсних чисел).

Отже, множина розв’язків однорідної СЛАР є лінійним простором.

Означення. Базис (синонім – основа).

Базисом чи фундаментальною сукупністю елементів лінійного простору V- називається така сукупність його об’єктів через які о д н о з н а ч н о можна виразити будь-який об’єкт лінійного простору з допомогою дій додавання та множення на число.

Вправа. Довести, що елементи базису лінійно незалежні. (Тому що нульовий елемент теж повинен отримуватися єдиним способом, тобто тільки коли всі коефіцієнти  .

ї з кутовим коефіцієнтом

Загальне рівняння прямої коли B≠0 можна звести до рівняння вигляду

y = k x + b

де k - кутовий коефіцієнт, який дорівнює тангенсу кута, утвореного даною прямою і додатним напрямком осі ОХ.

Рівняння прямої в відрізках на осях

Якщо пряма перетинає вісі OX і OY в точках з координатами (a, 0) і (0, b), то вона може бути знайдена, якщо використати формулу рівняння прямої в відрізках

x	+	y	= 1
a		b

Рівняння прямої, що проходить через дві різні точки на площині

Якщо пряма проходить через дві точки A(x₁, y₁) і B(x₂, y₂), такі що x₁ ≠ x₂ і y₁ ≠ y₂, то рівняння прямої можна знайти, використовуючи наступну формулу

x - x1	=	y - y1
x2 - x1		y2 - y1

Параметричне рівняння прямої на площині

Параметричне рівняння прямої може бути записане наступним чином

	x = l t + x0
	y = m t + y0

де (x₀, y₀) - координати точки, що лежить на прямій, {l, m} - координати напрямного вектора прямої.

Канонічне рівняння прямої на площині

Якщо відомі координати точки A(x₀, y₀), що лежить на прямій і напрямного вектора n = {l; m}, то рівняння прямої можна записати в канонічному вигляді, використовуючи наступну формулу

x - x0	=	y - y0
l		m

Приклад. Знайти рівняння прямо, що проходить через дві точки A(1, 7) і B(2,3).

Розв'язок. Використаємо формулу для рівняння прямої, що проходить через дві точки

x - 1	=	y - 7
2 - 1		3 - 7

Із цього рівняння виразимо y через x

x - 1	=	y - 7
1		-4

y - 7 = -4(x - 1)

y = -4x + 11

Тема 4 Криві другого порядку

24 Коло та його елементи

Колом називають геометричну фігуру, яка складається з усіх точок площини, рівновіддалених від даної точки. Цю точку називають центром кола, а відрізок, що сполучає центр кола з будь-якою точкою кола, називають радіусом.

Відрізок, що сполучає дві точки кола, називають хордою. Хорду, що проходить через центр кола, називають діаметром.

іаметр кола удвічі довший за радіус: d = 2r.

Розглянемо деякі властивості елементів кола.

1. Діаметр є найбільшою з хорд.

2. Діаметр з будь-якої точки видно під прямим кутом.

На малюнку 175: АВ — діаметр кола, М — довільна точка кола. Тоді  AMB = 90°.

3. Діаметр кола, перпендикулярний до хорди, ділить її навпіл.

4. Діаметр кола, що проходить через середину хорди, яка не є іншим діаметром, перпендикулярний до цієї хорди.

Коло — це фігура, що складається з усіх точок площини, рівновіддалених від деякої точки. Дана точка має назвуцентр кола.

Діаметр кола дорівнює двом її радіусам.

Діаметр кола, що перетинає хорду в її середині, є перпендикулярним до неї, і навпаки.

Рівні хорди знаходяться від центра кола на однаковій відстані (рівновіддалені). Рівновіддалені від центра кола хорди є рівними.

Довжина кола дорівнює двом радіусам, помноженим на константу π, що має наближене значення 3,14, або діаметру, помноженому на π.

Довжина кола С = 2πr або С = πd.

Кола, що мають спільний центр, називаються концентричними колами.

Кола, що мають рівні радіуси, є рівними.

Коло поділяє площину на зовнішню і внутрішню її частини.

Коло разом з внутрішньою його частиною площини називають кругом.

Круг має центр, радіус і діаметр ті ж, що й у кола.

Площа кола дорівнює квадрату його радіуса, помноженого на константу π: S = πr².

Коло — це одна з найважливіших фігур геометрії, яка відома людству з найдавніших часів. Уже Фалес у 6 столітті до нашої ери знав, що діаметр ділить коло навпіл.

Відношення довжини кола до його діаметра для всіх кіл є величиною сталою і позначається грецькою буквою π. Наближене значення числа π з 32 правильними десятковими знаками знайшов Рудольф Ван Цейлен, тому число π іноді називають Рудольфовим числом.

Тема 5 Границя функції

25 Основні теореми про границі

Нехай функція f(x)f(x) визначена у всіх точках проміжку (a;b)(a;b), за винятком, можливо, деякої точки x0∈(a;b)x0∈(a;b). Побудуємо послідовність значень аргументу функції f(x)f(x):

x1,x2,...,xn,...,n∈N,(xn≠x0) (1)x1,x2,...,xn,...,n∈N,(xn≠x0) (1)

таку, щоб всі члени послідовності належали проміжку (a;b)(a;b) і послідовність збігалась до точки x0x0:

limn→∞xn=x0.limn→∞xn=x0.

Тоді значення функції f(x)f(x)

f(x1),f(x2),...,f(xn),... (2)f(x1),f(x2),...,f(xn),... (2)

також утворять деяку числову послідовність.

Говорять, що число AA є границею функції f(x)f(x) при xx, що прямує до x0x0, якщо для будь-якої послідовності значень аргументу (1), яка збігається до числа x0x0, послідовність значень функції (2) збігається до числа AA, і пишуть

limx→x0f(x)=A.

Існує й інше, еквівалентне тому, що вище, визначення границі функції.

Говорять, що число AA є границею функції f(x)f(x) при xx, що прямує до x0x0, якщо для будь-якого додатнього числа εε знайдеться таке додатне число δδ, яке залежить від εε, що при всіх x∈(a;b)x∈(a;b), які задовільняють нерівність

0<|x−x0|<δ,0<|x−x0|<δ,

виконується нерівність

|f(x)−A|<ε.

Сформовані вище означення границі функції по Гейне і по Коші можуть бути узагальнені і на випадок, коли замість числа x0x0 береться +∞+∞ (або −∞−∞).

Говорять, що число AA є границею функції f(x)f(x) при xx, що прямує до +∞+∞, якщо для будь-якого додатнього числа εε знайдеться таке додатне число ΔΔ, що для всіх xx, які задовільняють нерівність x>Δx>Δ, виконується нерівність

|f(x)−A|<ε;|f(x)−A|<ε;

в цьому випадку пишуть

limx→+∞f(x)=A.limx→+∞f(x)=A.

Говорять, що функція f(x)f(x) прямує до +∞+∞ при прямуванні xx до x0x0, якщо для будь-якого скільки завгодно великого додатнього числа EE знайдеться таке додатне число δ>0δ>0, що для всіх xx, які задовільняють нерівність

0<|x−x0|<δ,0<|x−x0|<δ,

і таких, що належать області визначення функції, виконується нерівність

f(x)>E;f(x)>E;

в цьому випадку пишуть

f(x)→+∞ при x→x0, абоf(x)→+∞ при x→x0, або

limx→x0f(x)=+∞.

1) Якщо функції f(x)f(x) і g(x)g(x) мають границі при xx, який прямує до aa, то функції f(x)±g(x)f(x)±g(x), f(x)×g(x)f(x)×g(x), f(x)g(x)f(x)g(x) також мають границі при xx, який прямує до aa і

limx→a((f(x)±g(x))=limx→af(x)±limx→ag(x),limx→a((f(x)±g(x))=limx→af(x)±limx→ag(x),

limx→a((f(x)×g(x))=limx→af(x)×limx→ag(x),limx→a((f(x)×g(x))=limx→af(x)×limx→ag(x),

limx→af(x)g(x)=limx→af(x)limx→ag(x).limx→af(x)g(x)=limx→af(x)limx→ag(x).

В останньому випадку припускається, що функція g(x)g(x) не перетворюється в нуль в досить малому околі точки aa і

limx→ag(x)≠0.limx→ag(x)≠0.

2) Якщо при xx, що прямує до aa, функція f(x)f(x) має границю, рівну AA, і ця границя більше числа cc, то для достятньо близьких до aa значень xx функція f(x)f(x) задовільняє нерівність f(x)>cf(x)>c.
Тема 6 Неперервність функції

26 Дослідження функціїї на неперервність

Функція   називається неперервною в точці   , якщо вона в цій точці визначена і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції:   .

Функція   називається неперервною в точці   ,якщо виконуються наступні умови:

1) функція визначена в точці   ;

2) існує границя функції в точці   ;

3) значення функції в точці   співпадає із значенням границі в точці   .

Число А називається границею функції   справа при   ,     , якщо функція визначена у правому   - околі точки   , і для будь – якого   знайдеться таке   , що для всіх   , взятих з інтервалу   виконується нерівність   .

Позначають 

Число А називається границею функції   зліва при   ,     , якщо функція визначена у лівому   - околі точки   , і для будь – якого   знайдеться таке   , що для всіх   , взятих з інтервалу   виконується нерівність   .

Позначають 

Функція   називається неперервною в точці   ,якщо виконуються наступні умови:

1) функція визначена в точці   і в деякому околі цієї точки;

2) існують односторонні границі   і   ;

3) односторонні границі рівні між собою і дорівнюють значенню функції в точці   .

Тема 7 Похідна функції

27 Правила диференціювання

Правило 1. Похідна сталої дорівнює нулеві (сonst)¢ = 0.

Правило 2. Якщо u - будь-яка диференційовна функція від х і с - довільна стала, то(cu) ¢ = cu¢.

Правило 3. Якщо u та v - диференційовні функції від х, то їх сума u + v є диференційовною функцією:

Правило 4.Добуток двох диференційовних функ­цій u та v є диференційовною функцією

Правило 5. У точках, в яких , відношення двох дифе­ренційовних функцій є функція диференційовна, причому

Тема 8 Диференціал функції однієї змінної

28 Диференціал функції однієї змінної

Диференціалом n -го порядку ( n -м диференціалом) функції f (x) звуть диференціал від диференціала (n -1)-го порядку і позначають dⁿf=d(d^n-1f), nєN

Означення диференціалу функції Нехай функція у = f (х) диференційовна на деякому проміжку, тобто для будь-якої точки х з цього проміжку границя   існує і дорівнює скінченному числу. Враховуючи взаємозв’язок змінної величини, що має скінченну границю, і нескінченної малої величини, можемо записати   , де а — нескінченно мала величина ( при   та при   ). Помноживши всі члени останньої рівності на   , дістанемо 

Тема 9 Основні теореми диференціального числення

29 Теореми про монотонність функції, сталість на проміжку і екстремум та опуклість

Точка х0 називається точкою максимуму функції F(x), якщо для всіх значень аргументу х з деякого околу точки х0 значення функції менші або дорівнюють її значенню в точці х0.

Точка х0 називається точкою мінімуму функції F(x), якщо для всіх значень аргументу х з деякого околу точки х0 значення функції більші або дорівнюють її значенню в точці х0.

Точки мінімуму і максимуму функції називаються точками екстремуму функції.

Значення функції в точці максимуму називається максимумом функції. Значення функції в точці мінімуму називається мінімумом функції.

Мінімуми і максимуми функції називаються екстремумами функціями.

Крива y=f(x) називається опуклою на інтервалі , якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.

Крива y=f(x) називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.

Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої.

30 Дослідження функції та побудова графіка

1) знайти область визначення функції, тобто множину всіх точок для яких існує значення функції;

2) знайти (якщо вони існують) точки перетину графіка з координатними осями. Для цього потрібно у рівняння y=f(x) підставити x=0, а також розв'язати рівняння f(x)=0 для відшукання точок перетину з віссю абсцис Ox;

3) дослідити функцію на періодичність, парність і непарність. У деяких випадках це можна зробити візуально за самим виглядом функції, якщо ні - то проводимо перевірку:

4) знайти точки розриву та дослідити їх (такими точками є краї інтервалів визначення функції); 5) знайти інтервали монотонності, точки екстремумів та значення функції в цих точках;

6) знайти інтервали опуклості, вгнутості та точки перегину;

7) знайти асимптоти кривої;

8) побудувати графік функції.

Тема 10 Диференціювання функцій багатьох змінних

32 Частинні похідні, градієнт, повний диференціал

Частинною похідною від функції  за незалежною змінною х називається скінчена границя

,

обчислена при постійному у.

Повним диференціалом функції  називається сума добутків частинних похідних цієї функції та приростів відповідних незалежних змінних, тобто

.

Формулу диференціала можна записати у вигляді



або  .

Градієнтом функції   називається вектор, який показує напрямок найбільшого зростання функції і проекціями якого на
координатні осі   ,   ,   є відповідно   ,   ,   :

 .

Тема 11 Дослідження функцій багатьох змінних на екстремум, умовний екстремум

33 Дослідження функцій багатьох змінних на екстремум, умовний екстремум

Функція багатьох змінних u = f ( M ) має максимум ( мінімум ) в точці якщо існує такий окіл М ( сукупність точок , відстань яких до менша за певне додатне часло а ) , для всіх точок М виконується нерівність f ( M ) > ( < ) f ( ) при М відмінному від .

Екстремумами називають максимуми та мінімуми фінкції багатьох змінних її, а точки , яких вони мають мiсце -точками екстремуму .

Критичними точками для функції u = f ( називають точки , яких всі частинні похідні рівні нулю або не існують.

Тема 12-13 Невизначений та визначений інтеграл

34 Первісна. Таблиця невизначених інтегралів. Складання інтегральних сум при розв’язуванні практичних задач економічного характеру

Таблиця невизначених інтегралів:



Функція F(x) називається первісною для функції f(x) на проміжку І, якщо

на цьому проміжку F'(x) = f(x)

Тема 14 Диференційні рівняння першого порядку

35 Диференційні рівняння з роздільними змінними

Диференційне рівняння вигляду

• 
  н азивається рівнянням з розділеними змінними.
  

Однорідні диференційні рівняння, та рівняння, що до них зводяться

Однорідні диференційні рівняння можуть бути записані у вигляді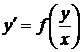

 , або  , де    і    - однорідні функції одного й того ж ступеня. Для розв’язання однорідного рівняння можна зробити заміну   , яка приводить до рівняння зі змінними, що розділяються.

Рівняння вигляду

зводиться до однорідного за допомогою перенесення початку координат в точку перетину прямих    і   . Якщо ці прямі не перетинаються, то   . Рівняння набуває вигляду    і зводиться до рівняння зі змінними, що розділяються заміною    або   .

Деякі рівняння можна звести до однорідних заміною   , де    - число, яке треба визначити з умови, щоб рівняння було однорідним. Якщо    не знаходиться з цієї умови, то рівняння не можна звести до однорідного вказаним способом

36 Диференційні рівняння першого порядку

Лінійним диференціальним рівнянням першого порядку називається рівняння виду y'+p(x)*y=g(x), де p(x) та g(x) – неперервні на певному проміжку функції.

Алгоритм методу Бернуллі

1.Розв'язок лінійного диференціального рівняння необхідно подати у вигляді добутку двох невідомих функцій y=u*v від аргумента u=u(x),v=v(x).Одну з цих функцій можна вибрати довільно, а друга визначається з даного рівняння.

2. За правилом похідна добутку рівна y=u*v,то y'=u'v+uv'.

3.Підставимо запис функції y=u*v та похідної y'=u'v+uv' у рівняння y'+p(x)*y=g(x) і одержимо u'v+uv'+p(x)*u*v= g(x). Згрупуємо другий і третій доданки, винісши спільний множник (u) за дужки і прийдемо до диф. рівняння u'v+u(v'+p(x)*v)=g(x).

4.Спершу визначаємо частинний розв'язок v=v(x), для цього розв'язуємо диф. рівняння v'+p(x)*v=0 і за довільну сталу інтегрування беремо нуль (С=0). Дане рівняння є диференціальним рівнянням з відокремлюваними змінними.

5. Далі підставимо знайдену функцію v=v(x) в вихідне диф. рівняння u'v+uv'+p(x)*u*v= g(x), яке при цьому спроститься до u'v+u*0=g(x), тобто до диференціального рівняння з відокремлюваними змінними u'v(х)=g(x) відносно u(x). З цього рівняння знаходимо u=u(x)+С.

6.Маючи u=u(x) і v=v(x), знаходимо загальний розв'язок через добуток y=u*v=( u(x)+С)* v(x).