1 .Физические основы механики. .Физические основы механики.
Механика изучает механическое движение, условия и причины, вызывающие данное движение, а также условия равновесия тел. Механическим движением называется изменение положения тела или его частей относительно других тел с течением времени.Механика Галилея-Ньютона называется классической механикой.В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью с изучаются релятивистской механикой, основанной на специальной теории относительности, сформулированной А.Эйнштейном (1879-1955). Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики неприменимы-они заменяются законами квантовой механики.
Квантовая механика-теория, устанавливающая способ описания и законы движения микрочастиц в заданных внешних полях; один из основных разделов квантовой теории. Квантовая механика впервые позволила описать структуру атомов и понять их спектры, установить природу химической связи, объяснить периодическую систему элементов и т. д. Т. к. свойства макроскопических тел определяются движением и взаимодействием образующих их частиц, законы квантовой механики лежат в основе понимания большинства макроскопических явлений.
Механика делится на три раздела: 1) кинематику; 2) динамику; 3) статику.
Кинематика раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих на них сил Динамика раздел механики, в котором изучается движение тел под действием приложенных к ним сил.
Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия.
Основные физ модели:.материальная точка-тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек. Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель-абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным.
Сплошна́я среда́-механическая система, обладающая бесконечным числом внутренних степеней свободы. Число степеней свободы-число независимых координат, полностью определяющих положение точки в пространстве.
1.1Элементы кинематики.
Всякое движение относительно. Характер движения зависит от того, относительно каких тел мы рассматриваем данное движение. Тело, относительно которого мы рассматриваем положение других тел в пространстве, называется телом отсчета. Системой отсчета называют систему координат, связанную с телом отсчета, и выбранный метод отсчета времени, т.е. часы.
Кинематическими уравнениями движения материальной точки называются уравнения (1.1).
При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

эквивалентными векторному уравнению r = r(t).(1.2)
Перемещение-вектор, соединяющий начальную и конечную точки траектории.
Скорость показывает простоту изменения тела в пространстве.Пусть моменту времени t1 соответствует радиус-вектор r1 движущейся точки, а близкому моменту времени t2 – радиус-вектор r2. Тогда за малый промежуток времени t точка совершит малое перемещение, равное s = r = r2 - r1. (рисунок – веторы r1, r2 выходят из нуля к точке 1, 2 на кривой; точки 1 и 2 соединены и образуют вектор deltaR; вектор средней скорости проходит через 1 и 2, а просто скорость выходит из точки по прямой). v (среднее) = < v > = s / t = r / t . Вектор средней скорости направлен вдоль вектора перемещения.
Более полно описать движение позволяет мгновенная скорость, т.е. скорость в любой момент времени. Она равна lim (при t 0) r / t = r ‘ ( t ). Вектор мгновенной скорости направлен по касательной траектории данной точки. Модуль полной скорости равен:
| v | = (корень) v2 по х + v2 по y + v2 по z
Кинематика движ по криволин траектории.Вектор ускорения при криволинейном движении тела обычно представляют в виде суммы двух составляющих, направленных следующим образом: одна по касательной к траектории – это тангенсальное ускорение, вторая по нормали к касательной –нормальное ускорение.
a (нормальное) = v (ст.2) / R
a (тангенсальное) = dv / dt
Итак,тангенциальнаясоставляющая ускорения характеризует быстроту изменения скорости по модулю(направлена по касательной к траектории), а нормальнаясоставляющая ускорения-быстроту изменения скорости по направлению (направлена к центру кривизны траектории)
Движение точки по окружности. При равномерном движении мат.точки по окружности радиус-вектор r точки описывает за время t равные углы . Отношение (вектор) / t = , называемое угловой скоростью, остается постоянным.
Если =const, то вращение равномерное и его можно характеризовать периодом вращения T-временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2. Так как промежутку времени t=T соответствует =2, то = 2/Т, откуда T=2/
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:E(вектор)=d(вектор)/dt
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору , при замедленном-противонаправлен ему
Связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а, нормальное ускорение аn) и угловыми величинами (угол поворота , угловая скорость (о, угловое ускорение ) выражается следующими формулами:S=R, v =R, а=R, аn=2=R
В случае равнопеременного движения точки по окружности (=const)
=0 +(-)t, =0 t+(-)t2/2 где 0 — начальная угловая скорость.
1.2Элементы динамики частиц
Динамика изучает движения тел и причины, вызывающие это движение.Чтобы решить основную задачу механики, необходимо выбрать рациональную систему отсчета и выяснить причины возникновения ускорений. Раздел механики, где решаются эти задачи называется динамикой. Механику, основанную на законах Ньютона называют классической механикой.
Масса тела-физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства.
Импульс тела – количество движения. P = m v (вектор) – справедливо для материальной точки. Если тело имеет конечный размер, то импульс этого тела можно найти как векторную сумму импульсов матерьяльных точек, на которое можно разбить это тело.
Сила – мера взаимодействия тел друг с другом. 4 вида взаимодействий:
1. Гравитационное – взаимодействие притяжения 2х тел, обладающих массой.
2. Слабые взаимодействия – ответственно за некоторые виды распада элементарных частиц, в частности за бета-распад.
3. Электро-магнитные взаимодействия – кулоновская и лоренцева силы.
4. Сильное взаимодействие – обеспечивает связь нуклонов в ядре.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние,он выполняется только в инерциальных системах отсчета.
Второй закон Ньютона. Ускорение, с которым движется тело прямо пропорционально силе, действующей на тело, и обратно пропорционально его массе и совпадает по направлению с действующей силой: a=F/m. Если на тело действуют несколько сил, то под F понимают результирующую всех сил. Движение твердого тела зависит не только от приложенных сил, но и от точки их приложения. Можно показать, что ускорение центра тяжести (центра масс) не зависит от точки приложения сил и справедливо уравнение maцт=F1+F2+F3+..., где m – масса тела, aцт – ускорение его центра тяжести. Если тело движется поступательно, то это уравнение полностью описывает движение тела.
Третий закон Ньютона:всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:F12=-F2I,где F12-сила, действующая на первую материальную точку со стороны второй; F21-сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
ИНЕРЦИАЛЬНАЯ система отсчета-в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения.Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета
НЕИНЕРЦИАЛЬНАЯ система отсчета-любая система отсчёта, которая движется как-либо ускоренно, или же вращается относительно инерциальной системы отсчета. Неинерциальность системы отсчета учитывают введением так называемых сил инерции.
Уравнение движения материальной точки: F=dp/dt
Уравнение динамики поступательного движения тела: 
где m – масса тела, a(вектор)– его ускорение,
суммаF(i-тое) – сумма всех действующих на тело сил.
Основное уравнение динамики вращательного движения твердого тела: I = M,где I– момент инерции твердого тела, относительно оси вращения, – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.
Г раницы применимости классического способа описания движения частиц:Законы движения Ньютона действуют только в ИСО, относятся к материальным точкам. раницы применимости классического способа описания движения частиц:Законы движения Ньютона действуют только в ИСО, относятся к материальным точкам.
1.6Элементы релятивистской динамики
Специальная теория относительности часто называется также релятивистской теорией, а специфические явления, описываемые этой теорией,-релятивистскими эффектами.
В основе специальной теории относительности лежат постулаты Эйнштейна, сформулированные им в 1905 г.
I.Принцип относительности: никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
II. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Первый постулат Эйнштейнаутверждает, что физические законы инвариантны по отношению к выбору инерциальной системы отсчета, а уравнения, описывающие эти законы, одинаковы по форме во всех инерциальных системах отсчета. Согласно этому постулату, все инерциальные системы отсчета совершенно равноправны, т. е. явления (механические, электродинамические, оптические и др.) во всех инерциальных системах отсчета протекают одинаково.
Согласно второму постулату Эйнштейна, постоянство скорости света-фундаментальное свойство природы, которое констатируется как опытный факт.
Специальная теория относительности потребовала отказа от привычных представлений о пространстве и времени, принятых в классической механике, поскольку они противоречили принципу постоянства скорости света. Потеряло смысл не только абсолютное пространство, но и абсолютное время.
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА имеют вид:K(система с корд x,y,z)
1.K->K’,(под знаком системы)x’=(x-ut)/корень1-2;y’=y;z’=z;t’=(t-ux/c2)/корень из1-2
2.K’->K, (под знаком системы)x=(x’+ut’)/корень1-2;y=y’;z=z’;t=(t’+ux’/c2)/корень из1-2;где =u/c
Они связывают координаты и время в различных инерциальных системах отсчета. В приделе при c к бесконечности, преобразования Лоренца переходят в преобразования Галилея. Различие в течение времени в разных инерциальных системах отсчета обусловлено существованием предельной скорости взаимодействий. При малых скоростях движений v0 преобразования Лоренца переходят в преобразования Галилея.
Следствия из преобразований Лоренца:
1.Сокращение длинны.
Пусть некоторый предмет находится в системе S`. Наблюдатель в системе S’ измеряя длину корабля получит: l’= x2’- x1’; x2’=гамма(x2-V t0); x1’=гамма(x1-V t0);l’= x2’- x1’=гамма(x2-V t0) - гамма(x1-V t0)=гамма(x2- x1)=гамма l;l’=гамма l=>l’< l0,l0)2 корень конец*с...Наблюдателю в системе S будет казаться, что все предметы в системе S’ сокращаются в направлении движения.Следствие: Расстояние между точками относительно. В соответствии с принципом относительности системы S и S’ равноправны, поэтому наблюдателю находящемуся в системе S’ также будет казаться, что все предметы в системе S сжимаются => расстояние между точками относительно.
2.Удлинение промежутков времени.
Пусть в системе S с координатой x0 произошло 2 события t1 и t2 (t1-включили прожектор, t2-выключили). t=t2 – t1
Наблюдатель в системе S` измеряя этот промежуток времени по своим часам, получит величину: t’=t2–t1; t’=(t2-(V*x0/ c2/корень из 1-2)- (t1-(V*x0/c2/корень из 1-2)=(t2–t1)/ корень из 1-2= t/корень из 1-2. t’>t.V=корень из 1-(t0/t)2корень конец*с.
Наблюдателю в системе S` будет казаться, что движущиеся относительно него в системе S процессы замедляются. Наименьшее значение имеет промежуток времени в той системе отсчета, в которой события происходят и относительно которой часы находятся в покое. Это время называют собственным.
Следствие: Относительность понятий одновременности.
3. Закон сложения скоростей:
Преобразования Лоренца позволяют получить: ИЗ U’x=dx’/dt’ и Ux=dx/dt следует что: Ux= (U’x+V)/(1+ (U’x*V)/ c2),следовательно при V/c<<1, Ux=U’x+V
Отсюда видно, что релятивистский способ сложения скоростей соответствует 2-му постулату специальной теории относительности: Скорость света во всех инерциальных системах отсчета одинакова.
Основной закон релятивистской динамики материальной точки имеет вид: F=d/dt*( m0*v/корень из 1–u2/c2)(39.2) или F=dp/dt(39.3),где p=mv=m0*v/корень из 1–u2/ c2 (39.4)-релятивистский импульс материальной точки.
Уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики. Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (39.4).В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Инвариантность уравнения движения относит преобразований Лоренца. Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости света, уравнение (39.2) переходит в основной закон классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<с. Законы классической механики получаются как следствие теории относительности для предельного случая v<<с (формально переход осуществляется при с). Таким образом, классическая механика-это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме)
Полную энергию можно выразить через массу покоя:E=m c2=(m0 c2)/корень из 1-V2/ c2=>E0=m0 c2-энергия покоя.
K=E-E0=m c2-m02= m0c2/корень из 1-2 - (m0 c2)=m0 c2*(1/корень из 1- (ст2)-1)
K= m0 c2*(m/m0-1)
K= m0 c2*(1/1-p2-1)
E2=(pc)2+(m0 c2)2
p2/2m=K(1+(K/2 m0 c2))
Если K<< m0c2,то K=p2/2m0=m0 V2/2
Закон сохранения четырехмерного вектора энергии-импульса.
Под знаком системы:m=m0/корень из 1-(u2/c2);E=m c2;p=mv,=> после преобразования Е2- p2*c2=m0c(c во всех системах одинакова).Смысл: 1координата-энергия,3остальных-проекции вектора импульса по осям
|
1.3Законы сохранения импульса и механической энергии.
ИЗОЛИРОВАННАЯ СИСТЕМА-механическая система тел, на которую не действуют внешние силы.
Рассмотрим механическую систему, состоящую из nтел, масса и скорость которых соответственно равны т1, m2, . .., тnи v1, v2, .. ., vn. Пусть F'1, F'2, ..., F'n — равнодействующие внутренних сил, действующих на каждое из этих тел, a f1, f2, ..., Fn — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из nтел механической системы:
d/dt(m1v1)=F'1+F1;d/dt(m2v2)=F'2+F2;d/dt(mnvn)= F'n+Fn.
Складывая почленно эти уравнения, получим
d/dt (m1v1+m2v2+... + mnvn) = F'1+F'2+...+ F'n+F1+F2+...+ Fn.
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то
d/dt(m1v1+m2v2 + ... + mnvn)= F1 + F2+...+ Fn, или
dp/dt=F1+ F2+...+ Fn, (9.1)
где  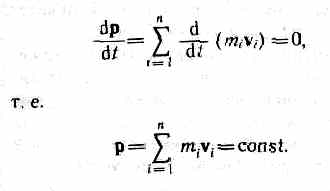 (*) (*)
импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (рассматриваем замкнутую систему)
(*)Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Центр инерциитела (системы материальных точек), точка, характеризующая распределение масс в теле или механической системе. При движении тела его центр масс движется как материальная точка с массой, равной массе всего тела, к которой приложены все силы, действующие на это тело.
Движение системы тел может быть охарактеризовано понятием центром масс.
Центром масс любой системы тел называется вектор, который определяются соотношением:R(i-тое(вектор))=сумма(i-тая)m(i-тая)*r(i-ый)/сумма(i-тая)m(i-тая). X(i-тое(вектор))=сумма(i-тая)m(i-тая)*x(i-ый)/сумма(i-тая)m(i-тая),аналогично и с координатамиY,Z
С корость движения центра масс: корость движения центра масс: => =>
Центр массы системы тел, движущихся, как материальная точка в которой сосредоточена вся масса системы.
Особенности:
1) FВНЕШН.=0, то dP=0 P=const
2)Если dt 0, то действие внешних сил очень мало dP=0, P=const
3) Fx =0, dPx=0, Px =const;
Реактивное движение.Уравнение Мещерского.
Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается за счет истечения газов, образующихся при сгорании топлива, и т. п.
Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени tмасса ракеты т, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за отрезок времени dt
dp = [(m-dm) (v+dv)+dm (v + u)]- mv,
где u — скорость истечения газов относительно ракеты. Тогда dp = mdv + udm
(учли, что dmdv-малый высшего порядка малости по сравнению с остальными).Если на систему действуют внешние силы, то dp = Fdt, поэтому Fdt = mdv + udm,mdv/dt=F-udm/dt.Член -udm/dt называют реактивной силой.Если u противоположен v, то ракета ускоряется, а если совпадает с v, то тормозится. Таким образом, мы получили уравнение движения тела переменной массы ma=F + Fp,которое впервые было выведено И. В.Мещерским.
Работа и кинетическая энергия. Мощность.
В качестве единой количественной меры различных форм движения материи и соответствующих им взаимодействий в физике вводится скалярная величина, называемая энергией.
Мощность-физическая величина N, измеряемая отношением работы A к промежутку времени t, в течение которого она совершена; если работа совершается равномерно, то N = A/ t.
Элементарной работой, силой F, называется величина, равная
dA = F * dr = F dr cos ; |dr| = ds ; Работа равна нулю в том случае, если: 1. тело неподвижно dr = 0 dA= 0. 2. =+ -/2, dA= 0.
dA>0, если – острый угол и dA< 0, если – тупой угол.
Вектор F (Fx, Fy, Fz) ; вектор dr (x, y, z) ; dA= F*dr = Fx*dx+Fy*dy+Fz*dz
A = (интеграл от 1 до 2) Fdr – работа силы по перемещению тела из 1 в 2.
Другой вариант записи – A = (интеграл от 1 до 2) Ft ds.
Кинетическая энергия мех системы–это энергия механического движения этой системы. Изменение кинетической энергии происходит за счет работы внешних сил.dT = dA. Используя второй закон Ньютона F=mdv/dt и умножая обе части равенства на перемещение dr, получим Fdr =m(dv/dt)dr=dA.Так как v=dr/dt,то dA=mvdv=mUvU=dT,откуда (интеграл от 0 до v)mUdU=mU2/2
Консервативные(поттенциальные) силы-силы,работа которых определяется только первоначальным и конечным положением тел и не зависит от траектории.
Диссипативне–силы,всегда направленные противоположно скоростям и совершающие отриц работуПотенциальная энергия. Работа, совершаемая потенциальными силами при изменениии конфигурации системы, т.е. расположении ее частей относительно системы отсчета не зависит от пути перехода из начального состояния в конечное. Эта работа A1-2 определяется только начальной и конечной конфигурацией систем, следовательно ее можно представить в виде разности значений некоторой функции конфигурации системы, называемой потенциальной энергией Wп. A1-2= П (1) – П (2) ; dA= - dП. В каждой конкретной задаче для получения однозначной энергетической зависимости каждой потенциальной рассматриваемой системы от ее конфигурации, выбирают нулевую конфигурацию, в которой потенциальная энергия системы считается равной нулю.
Потенциальной энергией механической системы называется величина, равная работе, которую совершают все действующие на систему потенциальные силы, при переводе системы из данного состояния в нулевое. dA= Fdr = Fx dx + Fy dy + Fz dz ; dA = - dП ;
dП = дП*dx / дх + дП*dy / дy + дП*dz / дz
dA = Fdr = Fxdx + Fydy + Fzdz = - дП*dx / дх - дП*dy / дy - дП*dz / дz
F = i * Fx + j * Fy + k * Fz = - (i *дП / дх + j *дП / дy + k *дП / дz) =
= - gradП
Потенциальная энергия материальной точки в однородном поле.
Силовое поле однородно, если сила F одинакова во всех точках поля. Рассмотрим однородный случай! Пусть сила F, приложенная к материальной точке действует вдоль оси Z ; dП = - dA = Fz dz ;
П = (интеграл z0 – z1) Fz dz = - Fz (z1 – z0) = -Fz * z ; Например тело в поле силы тяжести: F= mg ; z = h ; П = mgh
Закон сохранения энергии. Все законы сохранения связана с определенными свойствами симметрии пространства и времени. Закон сохранения импульса связан с однородностью пространства, т.е. вид физических знаков не изменяется при параллельном переносе в пространстве системы отсчета. Закон сохранения энергии связан с однородностью времени, т.е. выбор начала отсчета времени не изменяет физических законов или физические законы имвариантны относительно выбора начала отсчета времени.
Полной энергией называется сумма кинетической и потенциальной энергий. Механическая система называется консервативной, если все приложенные к ней непотенциальные силы не совершают работу, а все потенциальные силы постоянны во времени.
Потенциальная энергия системы может изменяться только за счет изменения ее консервации, поэтому если конфигурация системы не меняется, то П= const
дП / dt = 0. Рассмотрим консервативную систему, на которую действует внутренняя и внешняя консервативные силы и внешние диссепативные силы. Пусть вектор Fi – это внешняя консервативная сила, приложенная к внешней точке. Вектор Fi’ – внутренняя консервативная сила. Вектор f i – внешняя диссепативная сила. Запишем 2ой закон Ньютона для i-той точки матерьяльной системы: m i * dv i / dt = Fi + Fi’ + f i ; dr = v i * dt ; mi vi dt * dv / dt = (Fi’ + Fi) dvi + fi dri ; d (mi vi2 / 2) = (Fi’+Fi)dri+fidri
Для всей системы будет тоже самое, но ставится знак суммы перед каждым слагаемым. Отсюда следует d К + dП = dA ; d(К + П) = dA ;
A1-2 = (интеграл 1-2) d(К + П) ; A1-2 = (К + П)2 = - (К - П)1.
Если внешние силы не совершают работу, то dA=0 ; d (К + П) = 0 ;
т.е. полная энергия системы остается постоянной К + П = const
Согласно теореме Нетер, закон сохранения энергии соответствует однородности времени, закон сохранения импульса - однородности пространства.
1.5Принцип относительности Галилея
Установлено, что во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму; в этом суть механического принципа относительности (принципа относительности Галилея).
Для его доказательства рассмотрим две системы отсчета: инерциальную систему К (с координатами х, у, z), которую условно будем считать неподвижной, и систему К' (с координатами х', у', z'), движущуюся относительно К равномерно и прямолинейно со скоростью u (u=const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени tрасположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость и направлена вдоль ОО', радиус-вектор, проведенный из О в О', r0=ut.
Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 58 видно, что
r = r' + r0=r' + ut. (34.1)
Уравнение (34.1) можно записать в проекциях на оси координат: (под знаком системы X=X’+Ux*t, Y=Y’+Uy*t, Z=Z’+Uz*t)(34.2)
Уравнения (34.1) и (34.2) носят название преобразований координат Галилея.
В частном случае, когда система К' движется со скоростью v вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид(под знаком системы:X=X’+U*t,Y=Y’,Z=Z’)
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:t=t'. (34.3)
Продифференцировав выражение (34.1) по времени (с учетом (34.3)), получим уравнение
v = v' + u, (34.4)
которое представляет собой правило сложения скоростей в классической механике.
Ускорение в системе отсчета К: a=dv/dt=d(v’+u)/dt=dv’/dt=a’
Таким образом, ускорение точки А в системах отсчета К и К', движущихся друг относительно друга равномерно и прямолинейно, одинаково:а = а'. (34.5)
Следовательно, если на точку А другие тела не действуют (а = 0), то, согласно (34.5), и а' = 0, т.е. система K' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).
Таким образом, из соотношения (34.5) вытекает доказательство механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. являются инвариантными по отношению к преобразованиям координат. Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.
2.Механика колебаний и волн.
Колебательными называются процессы в той или иной степени повторяющиеся во времени. Виды колебаний:
Свободными колебаниями называются колебания, которые возникают в колебательной системе, в отсутствии внешних воздействий. Эти колебания возникают в следствии какого-либо начального наклонения колебательной системы от положения равновесия.
Вынужденные колебания – это колебания, возникающие в колебательной системе под влиянием переменного внешнего воздействия.
Колебания называют переодическими, если значения всех физических величин, характеризующих колебательную систему повторяется через равные промежутки времени. Наименьший промежуток времени, удовлетворяющий этому условию называется периодом колебания T.
Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы.
2.1Кинематика гармонического колебания.
Гармонические колебания-колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Гармонические колебания величины sописываются уравнением типа.
X(t)=Acos(0t+),X(t)-смещение частицы относительно положения равновесия в мом. Времени t, амплитудой колебаний(А)-максимальное значение колеблющейся величины ,круговая (циклическая) частота(число колебаний за 2 с) 0 = 2 / t = 2v, - начальная фаза колебаний-состояние колебательного процесса в определенный момент времени Так как косинус изменяется в пределах от +1 до -1, то s может, принимать значения от + А до -А.
Комплексная форма представления гармонич колебаний
В этом методе колеблющуюся величину представляют комплексным числом.Любое действительное число может быть представлено точкой на числовой оси.Комплексное число Z=x+iy.Согласно формуле Эйлера, для комплексных чисел,eiφ=cos+isin,где i=-1-мнимая единица. Модуль Z = корень из x2+y2=A;Z*=x-iy;Z=A(cos+isin),откуда Z(t)=A*e (в степени(i*(t+φ0))
В теории колебаний принимается, что колеблющаяся величина Z равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
Скорость гармонических колебаний U=dx/dt=-Asin(t+0).
Ускорение гармонических колебаний Umax=dU/dt=-2Acos(t+0)=-2*x.
Векторные диаграммы. Гармонические колебания изображаются графически методом векторных диаграмм: Если этот вектор привести во вращение с угловой скоростью w0, то проекция конца вектора будет перемещаться по оси х и принимать значения от -A до +А, а колеблющаяся величина будет изменяться со временем по закону s=Acos(w0t+j). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом j, равным начальной фазе, и вращающегося с угловой скоростью w0 вокруг этой точки.
Биения.два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть есть 2 колебания:x1=A1cos(ω1t+φ01),x2=A1cos(ω2t+φ02),ω2=ω1+Δω,Δω – очень мало
A=корень из A1+A2+2A1A2cos(φ). X=x1+x2=2Acos Δω*t/2 cos ωt,x=Aбиения cosωбt0;Aб=2Acos Δω*t/2.
Фигуры Лиссажу. Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний(рис)
|
1.4Элементы механики твердого тела.
Движение твердого тела
Условие равновесия твердого тела. Всякое движение твердого тела можно представить как сумму поступательного и вращательного движения. Отсюда вытекает 2 условия равновесия твердого тела: 1) F1+…+Fn = 0 – тело не движется поступательно ; 2) M1 +… Mk= 0 – тело не вращается.
Момент инерции тела относительно оси.
Моментом инерции матерьяльной точки относительно оси называется величина J = m r2. Где r – расстояние от точки до оси вращения.
К = m*v2/ 2. Если тело состоит из нескольких материальных точек, то момент его инерции будет равен сумме моментов инерций этих точек. Эта формула справедлива для дискретного распределения масс. В случае непрерывного распределения масс J = (интеграл) r2 dm .
Найдем момент инерции однородного сплошного цилиндра высотой h и радиусом Rотносительно его геометрической оси (рис.23). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом rи внешним-r+dr. Момент инерции каждого полого цилиндра dJ = r2dm(так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm-масса всего элементарного цилиндра; его объем 2rhdr. Если -плотность материала, то dm=•2rhdrи dJ=2r3dr.Тогда момент инерции сплошного цилиндра J=(интеграл)dJ=2h (интеграл от0доR)r3dr=1/2hR4
но так как R2h-объем цилиндра, то его масса m = R2h, а момент инерции J = 1/2R2.
Момент инерции стержня:J = 1/3 m l2
Момент инерции тонкого обруча: J = m R2
Момент инерции тонкого шара: J = 2/5 m R2
Момент инерции полого цил: J = (m R12+R21)
Момент инерции тонкого стержня: J = 1/12 m l2
Теорема Штейнера: Момент инерции тела относительно произвольной оси равен сумме момента инерции Jc относительно оси,параллельн данной и проходящей через центр масс тела,и произведения массф тела на квадрат расстояния между J = J центромасс + ma2.
Момент силы-величина,характеризующая вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и относительно оси. Момент силы относительно центра О-векторная величина, численно равная произведению модуля силы F на кратчайшее расстояние h от центра О до прямой, вдоль которой действует сила: M0= Fh ( h называется плечом силы). Вектор М 0 направлен перпендикулярно плоскости, проходящей через центр О и силу F, т. е. М 0 = [ rF], где r-вектор,проведенный из О в точку, где приложена сила F. Момент силы относительно оси ОО'-величина алгебраическая, равная проекции на эту ось момента силы относительно любой точки О на оси ОО' или численной величине момента проекции Q силы F на плоскость, перпендикулярную оси ОО', относительно точки пересечения этой оси с плоскостью.
Уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Найдем выражение для работы при вращении тела (рис). Пусть сила F приложена в точкеВ, находящейся от оси вращения на расстоянии r, — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d точка приложения В проходит путь ds= rd, и работа равна произведению проекции силы на направление смещения на величину смещения:dA=Fsinrd. (18.2) Учитывая (18.1), можем записать dA=Mzd,где Frsin = Fl =Mz— момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела идет на увеличение его кинетической энергии:dA=dT, но dT=d(Jz*2)/2)=Jzd.Учитывая, что =d/dt, получим Mz=Jz*d/dt=J.
Моментом импульса (моментом количества движения) материальной точки относительно оси называется векторная величина L = r * P ; где все величины – векторы ; r – расстояние от оси вращения до этой точки. Импульс точки: P = mv. Моментом силы M называется величина M=r *F
Моментом импульса твердого тела относительно оси является
L = сумма ri Pi ; |L| = |r | |P| sin ; Рассмотрим случай, когда =/ 2: L = сумма mi vi ri = сумма mi vi2 = J ; L = J ;
Продефференцируем это выражение по времени: dL / dt = J d/dt = J центромасс = M ; dL / dt = M ; Если M= 0, то dL / dt = 0 L = const
Это закон сохранения импульса!!!Если на систему тел не действует момент силы M или равнодействующая всех сил равна нулю, то момент импульса этой системы остается постоянным. Закон сохранения момента импульса является фундаментальным законом физики. Он справедлив не только в классической механике, но и в релитивистской и в квантовой механике. Закон сохранения момента импульса связан с изотропностью пространства-пространство обладает одинаковыми свойствами во всех направлениях.
3.Статистическая физика и термодинамика
Все вещества состоят из атомов и молекул, которые находится в непрерывном тепловом хаотическом движении. Характер этого движения зависит от агрегатного состояния вещества в твердых телах - это колебания ионов в узлах кристаллической решетки относительно положения равновесия. В газах – это ломаная линия. В жидкостях тепловое движение носит промежуточный характер, который сводится к тому, что молекулы находятся в определенном равновесном положении, перескакивают время от времени из одного положения в другое. Исторически имеются 2 подхода в молекулярной физике. Один называется статистическим, а второй – термодинамический. В 1-м случае рассматривается движение огромного числа частиц, во втором рассматривается макроскопические характеристики (давление, объем, температура, плотность). В основе 2-го подхода лежит эмпирические законы, которые называют началами термодинамики. Закон Авогадро: в одном моле вещества находится NA = 6.02 * 1023 частиц.
Т/д процесс – это переход термодинамической системы из одного состояния в другоес изменением т/д параметров. Термодинамический процесс называется обратимым, если после него можно возвратить систему в исходное состояние, при этом в исходное состояние должны вернуться и все тела, взаимодействующие с системой. Процесс, который не удовлетворяет этим условиям называется необратимым. Необходимым условием обратимого процесса является его равновестность, однако не всякий равновестный процесс обратим.
Стационарная система-состояние системы,параметры к-ой не изменяются со временем
Равновесная система-в к-ой состояние и параметры не изменяются
Релаксация-процесс перехода из НЕ равновесного состояния в равновесное
(время,по истечению к-ого т-д параметры системы изменится в е раз-время релаксации)
Обратимый процесс-к-ый возможно осуществить в обратном направлении, последовательно повторяя в обратном порядке все промежуточные состояния прямого процесса. Обратимым процессом может быть только равновесный процесс.
Равновесный проц-бесконечно медленный проц, в котором термодинамическая система проходит через ряд бесконечно близких друг к другу равновесных состояний. Равновесный процесс является обратимым.
Квазистатич-ий процесс-процесс,происходящий столь медленно, что термодинамическая система в течение всего процесса остается близкой к состоянию равновесия.
Циклический процесс-когда система принимает различные состояния,в итоге приходит к начальному состоянию.Т-д законы допустимы только для равновесных систем
2.2Гармонический осциллятор Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида: d2прs/dt2пр+w2пр0s=0.Свободные колебания такой системы представляют собой синусоидальное движение около положения равновесия.Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды
Физический маятник–это твердое тело, способное совершать колебания под действием своей силы тяжести вокруг оси, не проходящей через центр тяжести тела. Эта ось называется осью качания.
M = - J E ; M = m g d * sinφ (где d – расстояние от центромасс до места крепления физического маятника) ; J E = - mgd sinφ ; E = d2пр φ / dt2 ;
J * (d2пр φ / dt2) + mgd sinφ = 0 ; d2пр φ / dt2 + (mgd / J) sinφ = 0 ;
Это дифференциальное уравнение, описывающее колебания физического маятника. При малых углах уклонения можно считать, что sinφ = φ радиан ;
(d2пр φ / dt2) + mgdφ / J = 0 ; Это дифференциальное уравнение описывает гармонические колебания, частота которых равна:
d2пр S / dt2 + ω02 S = 0 ; ω02 = mgd / J ; ω0 = корень (mgd / J) ;
T = 2 / ω0 = 2 (корень J / mgd).
Если твердое тело представляет собой материальную точку, подвешенную на невесомой, нерастяжимой нити и способную совершать колебания, то маятник будет математическом. J = md2 ; T = 2 (корень md2 / mgd) = 2 (корень d / g); T = 2 (корень d / g) – период колебания математического маятника.
Пружинный маятник.-это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F=-kx, где k - коэффициент упругости, в случае пружины называемый жесткостью.ma = Fупр ; m * (d2пр x / dt2) = - kx ; (d2пр x / dt2) + kx / m = 0 – это дифференциальное уравнение, описывающее колебания груза на пружине, жесткость которого равна k. Частота этих колебаний: ω0= (корень) k / m ; Период: T=2 (корень m / k)
Кинетическая энергия записывается в виде:К=1/2m (dx/dt)2=1/2kA2sin2(ω0t+φ),
Потенциальная энергия П=1/2kx2=1/2kA2cos2(ω0t+φ),тогда полная энергия имеет значение:E=1/2kA2.
Свободные и затухающие колебания. Во всякой реальной колебательной системе всегда присутствует сила трения, которую также необходимо учитывать при рассмотрении колебания. При колебательном движении осциллятора им будет совершена работа против сил трения, в результате чего энергия колебаний будет постепенно уменьшаться и как следствие будет уменьшаться амплитуда колебаний. Свободные затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается из-за потерь энергии колебательной системой. Рассмотрим линейную колебательную систему – систему, параметры которой не изменяются в ходе колебаний. Рассмотрим колебания осциллятора, на который помимо квазе-упругих сил действует сила трения. Будем считать, что эта сила трения пропорциональна скорости колебания матерьяльной точки.
F= Fупр+Fтр ; Fупр = -kx ; Fтр = -b * dx/dt ; m * d2 x / dt2= -b*dx/dt – kx
Уравнение, описывающее затухающие колебания:
(d2пр x / d t2) + b/m * dx/dt + kx / m = 0 ; Введем обозначения:
ω02 = k/m ; b/m = 2; = b/2m; b – коэффициент сопротивления ; (d2 x / dt2) + 2*dx/dt + ω02 x = 0 ;
– коэффициент затухания. (из-за диссипации(рассеяние) энергии благодаря силам вязкого трения для механических затухающих колебаний)
Общее решение этого уравнения будем искать в виде X = A e (ст.ЛЯМДА t).
Подставим это решение в дифференциальное уравнение затухающих колебаний: dx/dt = A ЛЯМДА e (ст. ЛЯМДА t) ; d2пр x / dt2 = A ЛЯМДА (ст.2) e (ст. ЛЯМДА t); A ЛЯМДА (ст.2) e (ст. ЛЯМДА t) + 2bA ЛЯМДА e (ст.ЛЯМДА t) + ω02 A e (ст.ЛЯМДА t) ; Сокращаем:
ЛЯМДА (ст.2) +2А d + ω02 = 0 – характеристическое уравнение.
Решая его, получаем: X = - + - (корень 2 – w 0 (ст.2)) =
- + - i (корень ω02 – 2) ; Таким образом общее решение исходного дифференциального уравнения можно преобразовать к виду: w = (корень ω02 – 2 ); X (t) = A0 e (ст. – t) sin (wt + 0) ;
(рисунок – график затухающих колебаний – сжатый синус, все ниже и неже стает по оси OY)..Затухающие колебания не являются периодическими, т.к. максимальное значение колеблющихся величин, достигаемое в некоторый момент времени в последующем никогда не повторяется, поэтому можно говорить об условном периоде затухающих колебаний – T = 2 / ω = 2 / (корень ω02 – 2). Если >= ω0, то процесс становится апериодическим.
Логарифмический декремент затухания.
δ = ln (A(t) / A(t + )) = ln (A0 e (ст. – t) / A0 e (ст. – (t + ))) = ln (A0 e (ст. – t) / A0 e (ст. – t) e (ст. – )) =T ;
δ = T = 1 / N ; Время релаксации () в течении которого амплитуда затухающих колебаний убывает в e раз ; A = A0 / e = A0 e (ст. – ) ; e (ст. - 1) = e (ст. – ) – = 1 ;
= 1 / ; N = / T – число колебаний, в течении которых амплитуда убывает в e раз ; δ = 1 / N ;
Добротность. Q = [2 W (t)] / [W (t) – W (t + T)]; Добротность Q – это величина, пропорциональная отношению энергии, запасенной в колебательной системе к уменьшению этой энергии за один период. Т.к. энергия, запасенная в колебательной системе пропорциональна квадрату амплитуды, то: Q = 2 A (ст.2) (t) / A (ст.2) (t) – A (ст.2) (t +T);
A = A0 e (ст. – t) ; Q=2 A0 e(ст.-2 t) / A0 (ст.2) e(ст. –2 t) – A0 e (ст.-2 (t + T)) ; Q = 2 / (1 – e (ст. –2 t)) ; Q= / δ – при малых затуханиях.
Вынужденные механическими-колебания, возникающие под действием внешней периодически изменяющейся(вынуждающей) силы F(t)=F0cosωt; воспользуемся 2-ым законом Ньютона:
mx(сверху 2 точки)=-kx-rx(сверху 1 точка)+F0cost;x(сверху 2 точки)+2x(сверху 1 точка)+ω02x=F0cost/m.Они происходят с частотой ω вынуждающей силы
A(ω)=числитель(F0/m),знаменат(корень из (ω02-ω2)2+44ω4 (*1)При ωрез=корень из ω02-2 2(*2),амплитуда достигает максимального значения…На рисунке 2>1
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте wрез При 2<2 значение wрез практически совпадает с собственной частотой w0 колебательной системы.Подставим (*2)в (*1),получим:
Aрез=x0 /(2 на корень из ω02-2)
|
 Скачать 0.73 Mb.
Скачать 0.73 Mb.