Энтропия. Помимо внутренней энергии, которая является только функциональной составляющей термодинамической системы, в термодинамике используется еще ряд других функций, описывающих состояние термодинамической системы. Особое место среди них занимает энтропия. Пусть Q – теплота, полученная термодинамической системой в изотермическом процессе, а T – температура, при которой произошла эта передача теплоты. Величина Q/ T называется приведенной теплотой. Приведенное количество теплоты, сообщаемое термодинамической системе на бесконечно малом участке процесса будет равно dQ / T. В термодинамике доказывается, что в любом обратимом процессе сумма приведенных количеств теплоты, передаваемая системе на бесконечно малых участках процесса равна нулю. Математически это означает, что dQ/T – есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от того, каким путем перешла система в такое состояние. Функция, полученный дифференциал которой равен dS= dQ/ T – называется энтропией. Энтропия определяется только состоянием термодинамической системы и не зависит от способа перехода системы в это состояние. S – энтропия. Для обратимых процессов delta S = 0. Для необратимых delta S > 0 – неравенство Клаудио. Неравенство Клаудио справедливо только для замкнутой системы. Только в замкнутой системе процессы идут так, что энтропия возрастает. Если система незамкнута и может обмениваться теплотой с окружающей средой, ее энтропия может вести себя любым образом ; dQ = T dS ; При равновестном переходе системы из одного состояния в другое dQ = dU + dA ; delta S = (интеграл 1 – 2) dQ / T = (интеграл) (dU + dA) / T. Физический смысл имеет не сама энтропия, а разность энтропий при переходе системы из одного состояния в другое.
Статистическая природа энтропии.
Физический смысл энтропии был раскрыт Больцманом, который связал энтропию с термодинамической вероятностью w, S=k*lnW,где w - это число способов которыми может быть реализовано данное состояние термодинамической системой. Энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесии-наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.
Теорема Нернста: при стремлении температуры к абсолютному нулю энтропия системы стремится к нулю при прочих фиксированных условиях (напр., при неизменных объеме или давлении) (В. Нернст, 1906). Другая формулировка: при помощи конечной последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю.limS(T->0)=0
Связь энтропии с вероятностью состояния системы. Более глубокий смысл энтропии скрывается в статической физике. Энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы. Иными словами W – это число микросостояний, которые реализовывают данные макросостояния.
Больцман методами статистической физики показал, что энтропия S системы и термодинамическая вероятность связаны соотношением: S= k ln (W) ; где k – постоянная Больцмана. Термодинамическая вероятность W не имеет с математической вероятностью ничего общего. Из этого соотношения видно, что энтропия может рассматриваться как мера вероятности состояния термодинамической системы, энтропия является мерой неупорядоченной системы. Чем больше число микросостояний, реализующих данное макросостояние, тем больше ее энтропия.
Второй закон термодинамики. Количество теплоты, полученное от нагревателя, не может быть целиком преобразовано в механическую работу циклически действующей тепловой машиной. Это и есть 2ой закон: в циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от источника энергии – нагревателя. (by Кельвин Copyright 1851). Второй закон связан с необратимостью процессов в природе. Возможна другая формулировка: невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от холодного тела к горячему. Второй закон имеет вероятный характер. В отличие от закона сохранения энергии, второй закон применим лишь к системам, состоящим из очень большого числа частиц. Для таких систем необратимость процессов объясняется тем, что обратный переход должен был бы привести систему в состояние ничтожно малой вероятностью, практически не отличимой от невозможности.
Самопроизвольные процессы в изолированной системе всегда проходят в направлении перехода от маловероятного состояния в более вероятное.
|
3.4Элементы термодинамики
Внутренняя энергия газа состоит из учета потенциальной энергии и кинетической энергии движения атомов или молекул, поэтому величина внутренней энергии определяются выражением:U=NEk(вектор),тк N=m*NA/M ; Ek=i*kT/2 ; k=R/NA ; U=(mNA/M)*(ikT/2)=ivRT/2 ; Внутренняя энергия – это функция состояния газа. Она прямо пропорциональна абсолютной температуре и характеризует энергию всех молекул газа.
Закон равномерного распределения энергии по степеням свободы Числом степеней свободы называют количество независимых координат, которые определяют положение тела в пространстве. Точка в пространстве имеет 3 координаты и имеет 3 степени свободы. Твердое тело имеет 3 степени свободы, центра инерции и 3 вращательных степени свободы. Молекулы идеального газа имеют среднюю кинетическую энергию Ek=3/2kT
Таким образом, на одну степень свободы приходится kT/2. Этот закон очевиден для идеального газа и справедлив для любого случая и гласит, что на одну степень свободы в среднем приходится одинаковое количество энергии равное kT/2.
1)i =3 – одноатомный ; 2)i =3+2=5 – 2-х атомный ; 3)i=3+3=6 – 3-х атомный и более ; 4)i=3N-6,где N-число атомов.Для многоатомного газа:
Работа газа при изменении его объема
Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде . Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работу
A=Fdl=pSdl=pdV,где S — площадь поршня, Sdl=dV— изменение объема системы. Таким образом,A=pdV.Полную работу A, совершаемую газом при изменении его объема от V1до V2, найдем:интеграл(V1-V2)pdV
Теплоемкость
Удельная теплоемкость вещества величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:c=Q’/mdT
Молярная теплоемкость- величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К;C=Q’/vdT
где v = m/M — количество вещества, выражающее число молей.
В газе различают теплоемкости при постоянном давлении и теплоемкость при постоянном объеме.
1) V=const ; dV=0 ; dA=PdV=0 ; dQ=dU ; Ev = dQm / dT ; Eт = dUm / dT ;
Um = i k T Na/ 2 = i R T / 2 ; где i – число степеней свободы ;
dUm = i R dT / 2 ; Ev = i R / 2 – теплоемкость при постоянном V ;
2) P = const ; dAm = dm + dA ; dA= pdV ; PV=RT ; PdV= RdT ;
dQm = Cv dT + RdT = Cv + RdT ; Cp = dQm / dT= Cv +R ; Cp= Cv +R - уравнение Майера ; Cp = (iR / 2) + R = ((i +2)/ 2) R ; Cp = ((i+2) / 2) R ;
γ = Cp / Cv = (i+2) / i – коэффециент Пуассона
Из полученной формулы видно, что теплоемкость газа не зависит от температуры. Эксперементально было установленно, что этот закон соблюдается в достаточно широком интервале температур только для одноатомных газов
Первое начало термодинамики или первый закон термодинамики.
dQ = dU + dA ; Теплота, подводимая к термодинамической системе идет на изменение внутренней энергии и на совершение работы.
Внутренняя энергия U определяется только состоянием термодинамической системы, а Q и A являются характеристиками процесса при котором система переходит из одного состояния в другое. Переход системы из одного состояния в другое может осуществляться различными путями, поэтому Q и A зависят от способа перехода системы из одного состояния в другое, в то время, как внутренняя энергия U определяется только состоянием системы и не зависит от того, каким путем система перешла в это состояние.
Применение 1-го начала термодинамики к изопроцессам и адиабатическому процессу.
1) V = const изохорный => dV=0 ; d = PdV=0 ; dQ=dU ; dU = МЮ dUмол = МЮ Cv dT ;
dQ= МЮ Cv dT ; Q = (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T2 – T1) – m Cv (T2 – T1)/ μ
2) T = const изотермический => dT= 0 ; dQ= МЮ Cv dT = 0 ; dQ = dA ;
dA = PdV ; PV = МЮ RT ; P= МЮ RT / V ; dA = МЮ RT dV / V ;
A = (интеграл V1 – V2) МЮ RTdV / V = МЮ RT (интеграл V1 – V2) dV/ V = МЮ RT ln (V2/ V1) = МЮ RT ln (P1/ P2) ; P1 V1 = P2 V2 ;
3) P = const изобарический => dQ = PdV ; A = (интеграл V1 – V2) PdV = P (V2 – V1) ; A = P (V2 – V1) ; dU = МЮ Cv dT ; PdV = МЮ RdT ; dQ = МЮ Cv dT + МЮ Rdt = МЮ (Cv + R) dT ; Q = МЮ Cp (T2 – T1) ;
4) Q = const Адиабатный dA = dU ; dA = МЮ Cv dT ; PdV = - МЮ Cv dT ; PV = МЮ RT – продифференцированное уравнение Менделеева-Клайперона ; PdV + VdP = МЮ R dT ; … ; lnP = - γ lnP + const ; γ – коэффициент Пуассона ; lnP + lnV (ст. γ) = const ; PV (ст. γ) = const ; (график такой же как и изотермический, только чуть выше вверх).
dA = - dU = - МЮ Cv dT ; A = - (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T1 – T2) ;
Адиабатический процесс-т-д процесс, при котором система не получает теплоты извне и не отдает ее. PV(ст )=const
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необртимым.
Циклический процесс-когда система принимает различные состояния,в итоге приходит к начальному состоянию.Т-д законы допустимы только для равновесных систем
Цикл Карно.В основе идеальной тепловой машины лежит круговой процесс который называется циклом Карно
1-2: A1=Q1>0 – Изотерм. расширение
2-3: Q=0 – Адиабатическое расширение;
3-4: A2=Q2<0 – Изотермическое сжатие;
4-1: Q=0 Адиабатическое сжатие.
Для замкнутых циклов работа совершаемая газом в цикле Карно равна подводимому теплу. Тепловая машина реализующая этот цикл имеет максимальный КПД по сравнению с любым другим циклом. =(T1-T2)/T1; Для повышения КПД тепловых машин Необходимо увеличивать температуру нагревателя и уменьшать температуру холодильника. КПД любой реальной тепловой всегда меньше, чем у машины Карно: T1-T2 / T1>=Q1-Q2/Q1
КПД для кругового процесса:=A/Q1-Q1-Q2 /Q1=1-Q2 / Q1(*),где где Q1— количество теплоты, полученное системой, q2— количество теплоты, отданное системой.Подставляя значение работы из 1 в 2: A12=mRT1/M*lnV2/V1=Q1 ; и A34=mRT2/M*lnV4/V3= - Q2 в формулу(*),и учитывая что V2/V1= V3/V4, получим:=Q1-Q2/Q1=в числителе mRT1/M*lnV2/V1- mRT2/M*lnV3/V4,в знаменателе mRT1/M*lnV2/V1=T1-T2/T1.
|
3.5Реальные газы,жидкости и кристаллы
РЕАЛЬНЫЙ ГАЗ-газ, свойства которого существенно зависят от взаимодействия молекул.
МЕЖМОЛЕКУЛЯРНОЕ ВЗАИМОДЕЙСТВИЕ, взаимодействие между молекулами с насыщенными химическими связями.
При рассмотрении реальных газов-газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях 10-9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.
Коэффицент сжимания PV/RT=1.Идеальный газ тем ближе к реальному,чем >его температура и < коэф. сжатия.
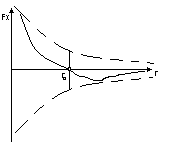
Fx=-dw(потенц. энергия взаимодействия)/dr(молекулярная энергия взаимодействия) r – расстояние, r0 – равновесное расстояние.
kT<Eпотmin- то расстояние между молекулами малы
kT>>WEпотmin- то степень свободы молекул и расстояние между молекулами больше
Уравнение Ван-дер-Ваальса.
Учет межмолекулярных взаимодействий был произведен впервые голландским физиком Ван-дер-Ваальсом. При этом он исходил из простой модели, которая была основана на следующих положениях:
1)Молекулы газов представляют собой шары с эффективным диаметром.
2)Между молекулами существуют только силы притяжения
3)Силы отталкивания учтены введением эффективного диаметра.
Учет собственного объема молекулы
V=1/6 l3 приводит к тому, что «Свободный» молярный объем в сосуде уменьшается по сравнению с идеальным газом на величину b,
V*= V-b где b – постоянная Ван-дер-Ваальса. b=rNAv
Наличие сил притяжения между молекулами реального газа приводит к тому, что давление становится меньше на некоторую величину p*. Таким образом pид=p+p*.Величина p* согласно теории Ван-дер-Ваальса обратно пропорциональна квадрату объема: p*=a/V2, т.о. уравнение состояния имеет вид: (p+a/V2)(V-b)=RT
Для разреженных газов размерами атомов можно пренебречь. Уравнение Ван-дер-Ваальса переходит в обычное уравнение Менделеева-Клапейрона.
Переход вещества из газообразного состояния в жидкое или твердое. Конденсация возможна только при температурах ниже критической температуры.КРИТИЧЕСКАЯ ТЕМПЕРАТУРА-предельная температура равновесного сосуществования двух фаз (жидкости и ее пара), выше которой эти фазы неразличимы.КРИТИЧЕСКОЕ СОСТОЯНИЕ-состояние двух равновесно сосуществующих фаз, при достижении которого фазы становятся тождественными по своим свойствам. Критическое состояние характеризуется критическими значениями температуры, давления, удельного объема, развитием флуктуаций. В критическом состоянии системы жидкость-пар удельные объемы жидкой и паровой фаз становятся одинаковыми, теплота фазового перехода обращается в нуль, исчезают граница раздела фаз и поверхностное натяжение. Поэтому критическое состояние можно рассматривать как предельное состояние однофазной системы. Сжимаемость системы жидкость-пар в критическом состоянии очень велика, вследствие чего резко возрастают флуктуации плотности и наблюдается критическая опалесценция.
Фаза-однородная по химическому составу и физическим свойствам часть термодинамической системы, отделенная от др. частей (фаз), имеющих иные свойства, границами раздела, на которых происходит изменение свойств.
Твердые тела (кристаллы) характеризуются наличием значительных сил межмолекулярного взаимодействия и сохраняют постоянными не только свой объем, но и форму. Кристаллы имеют правильную геометрическую форму, которая является результатом упорядоченного расположения частиц (атомов, молекул, ионов), составляющих кристалл. Структура, для которой характерно регулярное расположение частиц с периодической повторяемостью в трех измерениях, называется кристаллической решеткой. Точки, в которых расположены частицы, а точнее-точки, относительно которых частицы совершают колебания, называются узлами кристаллической решетки
Фазовый перед I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы 1 рода характеризуются постоянством температуры, изменениями энтропии и объема. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. В подобных переходах-из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние - степень беспорядка увеличивается, т. е., согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.
Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объема, называются фазовыми переходами II рода. Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Общая трактовка фазовых переходов II рода предложена советским ученым Л. Д. Ландау (1908—1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов II рода являются: переход ферромагнитных веществ (железа, никеля) при определенных давлении и температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое
скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия (гелия I) при Т — 2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести.
|
|
 Скачать 0.73 Mb.
Скачать 0.73 Mb.