Шпора по физике [1 семестр]. 1. Физические основы механики. Механика
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
| 1.1.движение точки по окружности 1.4.момоент инерции 1.4 Уравнение динамики вращательного движения твердого тела 1.4 Моментом импульса (количества движения) 1.5Принцип относительности Галилея 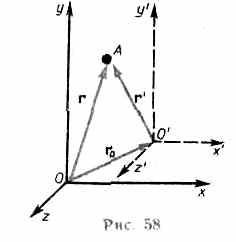  3. Закон сложения скоростей(1.6Элементы релятивистской динамики) 3. Закон сложения скоростей(1.6Элементы релятивистской динамики)Комплексная форма представления гармонич колебаний  2.1.Векторные диаграммы  2.1.БИЕНИЯ 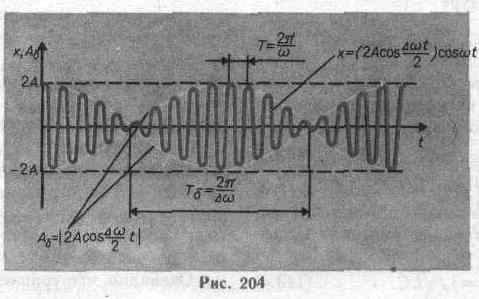 2.1ФИГУРЫ Лиссажу 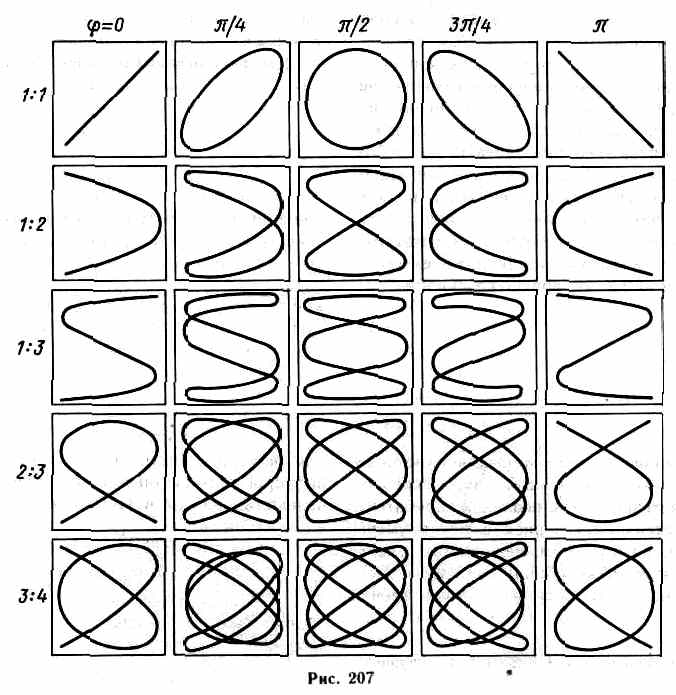 2.2Вынужденные механическими-колебания  3.1Элемненты МКТ  ЦИКЛ КАРНО 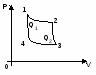 | 2.3Волновые процессы Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.Упругие волны возможны только в упругой среде, в жидкостях и газах–продольные,в твердых телах-и продольные и поперечные Поперечные волны – это волны, в которых смещение количества частиц происходит перпендикулярно направлению распространения волны. Продольные волны – это волны, в которых смещение количества частиц происходит в направлении распространения волны. Поперечные волны могут возникать в средах, в которых появляются упругие силы при деформации сдвига. В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид y(x,t)=Acos[w(t -х/v)+j0], где А=const — амплитуда волны, w — циклическая частота волны, j0 — начальная фаза колебаний, определяемая в общем случае выбором начал отсчета х и t, [w(t-x/v)+j0]—фаза плоской волны. Длинна волны-расстояние, между ближайшими частицами, колеблющимися в одинаковой фазе. Волновой вектор-вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу Фазовый фронт-геометрическое место точек, имеющих одну и ту же фазу. Волново́е число́ -это величина, обратная длине волны, т. е. это число волн на отрезке 2π..Формула k = 2π/лямда. Фа́зовая ско́рость-скорость перемещения фазы волны в пространстве вдоль заданного направления. Зачастую рассматривают направление, совпадающее с направлением волнового вектора.Так для случая плоской гармонической волны фазовую скорость вдоль волнового вектора можно выразить следующим образом: Uk= ω/k, где k-волновое число, ω - угловая частота. Если среда, в которой распространяются одновременно несколько волн линейно, т.е. ее свойства не зависят от возмущений, создаваемых волнами, то к этой среде применим принцип суперпозиции: при распространении нескольких волн в среде, каждая из них распространяется независимо от других, а результат их совместного действия является простой суммой действия каждой из этих волн. Исходя из принципа суперпозиции любая волна может быть представлена в виде суммы гармонических волн, т. е. в виде волнового пакета, или группы волн. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Групповая скорость.«Сконструируем» простейший волновой пакет из двух распространяющихся вдоль положительного направления оси х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем d<< и dk<<k.Тогда:y=A0cos(t-kx)+A0cos[(+d)t-(k+dk)x]=2A0cos((td-xdk)/2)*cos(t-kx). Эта волна отличается от гармонической тем, что ее амплитуда есть медленно изменяющаяся функция координаты х и времени t.За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что td-xdk=const, получим dx/dt=d/dk=u.Скорость uесть групповая скорость. Ее можно определить как скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет. Интерференция волн-перераспределение энергии в пространстве,с устойчивым во времени образованием максимумов(x=n) в одних точках и минимумов(x=/2(2n+1)) в других Стоячие волны-это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами Бегущая:y1=Acos(t-kx);Отраженная:y2=Acos(t-kx);сложим:y=2Acos2x/*sint ЭНЕРГИЯ УПРУГИХ ВОЛН Упругие волны переносят энергию, которая равна сумме кинетической и потенциальной энергии всех составляющих частиц среды, где происходят колебания. Т.к. среда может быть бесконечной, удобно определять энергию волны через энергию, приходящуюся на единицу объема. КV=mU2/2=VU2/2; |U|=Asin(t-2x/).Wk(удельная плотность энергии)=КV/V=1/22A2sin2(t-2x/); Wk=Wп;W=Wk+Wп=2A2sin2(t-2x/) Видно, что плотность энергии зависит от времени. Это значит что в процессе распространения колебаний энергия изменяется от 0 до Wmax=rw2A2, что соответствует моментам полной отдачи энергии соседним участкам среды (0) и получении новой порции энергии от источника. ВЕКТОР УМОВА.Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии.Этот вектор для упругих волн называется вектором Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. p(вектор)=wU(вектор),где p=dE/(dt*dS)-энергия,распространяющаяся через единицу площади,перпенд-но к поверхн за единицу времени(плотность потока энергии),а w=dE/dV-энергия,заключенная на единицу обьема(обьемная плотность) Эффект Доплера-изменение частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника друг относительно друга. Например, из опыта известно, что тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении, т. е. движение источника колебаний (гудка) относительно приемника (уха) изменяет частоту принимаемых колебаний. 1. Источник и приемник покоятся относительно среды, , т.е. vист=vпр=0. Если v-скорость распространения звуковой волны в рассматриваемой среде, то длина волны =vT=v/v0. Распространяясь в среде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой =v/=v/(vT)=0 2. Приемник приближается к источнику, а источник покоится, т.е. vпр>0, vист=0. В данном случае скорость распространения волны относительно приемника станет равной v+vпр. Так как длина волны при этом не меняется, то v=U+Uпр/= U+Uпр/UT=(U+Uпр)v0/U 3.Источник приближается к приемнику, а приемник покоится, т.е. vист>0, vнаб=0. Скорость распространения колебаний зависит лишь от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние vT(равное длине волны ) независимо от того, движется ли источник или покоится. За это же время источник пройдет в направлении волны расстояние vистT, т.е. длина волны в направлении движения сократится и станет равной '=-vистТ=(v-vист)Т, тогда v=U/’=U/((U-Uист)T)=Uv0/(U-Uист) 4. Источник и приемник движутся относительно друг друга. Используя результаты, полученные для случаев 2 и 3, можно записать выражение для частоты колебаний, воспринимаемых источником: v=((U±Uпр)v0)/(U±Uист) Эффект Доплера различен в зависимости от того, движется ли источник или приемник. | 3.1Элемненты МКТ Макоскопическое сосотояние системы, определяется значениями ее термодинамических параметров: давления p, температуры Т, удельного объема v, внутренней энергии U и т. п. Для определения макроскопического состояния однокомпонентной системы достаточно знать значения любых 2 независимых параметров (напр., Т и p или Т и v).. Идеальным газом называют газ, в котором отсутствуют взаимодействие между молекулами и размеры атомов пренебрежимо малы (материальные точки), атомы или молекулы совершают упругие соударения со стенками сосуда. При этих условиях молекулы идеального газа оказывают силовое воздействие на стенки сосуда, которое характеризуется физической величиной называемой давлением. P=F/S, Па. Давление – сила, действующая на единицу поверхности. Основное уравнение МКТ. P1(вектор)=F1(вектор)*t ; F1молекулы=2m1Ux/t Fвсех мол=2m1Ux/t*n*SUxt*1/2 ; U2x=1/3 U2, откуда имеем основные уравнения идеального газаP=F/S*1/3n m1<U2>; P=2/3n Температура-физическая величина, характеризующая состояние термодинамического равновесия системы. Температура всех частей изолированной системы, находящейся в равновесии, одинакова. Если система не находится в равновесии, то между ее частями, имеющими различную температуру, происходит теплообмен. Более высокой температурой обладают те тела, у которых средняя кинетическая энергия молекул (атомов) выше. Измеряют температуру термометрами на основе зависимости какого-либо свойства тела (объема, электрического сопротивления и т. п.) от температуры 3.2Функции распределения в классической физике Микроскопическое состояние системы, определяется в классической механике заданием координат и импульсов всех частиц системы. Вероятность и флуктуации. Пусть имеется совокупность из очень большого числа одинаковых частиц, находящихся в равновесном состоянии. Это равновесное состояние характеризуется определенным значением давления среднеквадратичной скорости и т.д., однако за счет того, что молекулы хаотически двигаются и соударяются между собой возникает случайное отклонение мгновенных значений этих величин от их средних значений. Эти случайные отклонения называются флуктуациями. Вероятность-число, пропорциональное количеству физически различимых микроскопических состояний, которыми может быть реализовано данное макроскопическое состояние системы. Распределения Максвелла молекул по скоростям. Очевидно, что число молекул с очень маленькими скоростями, как и число молекул с очень большими скоростями сравнительно невелико. Основное количество молекул имеет скорости близкие к КВ Распределение по скоростям установил Максвелл. Для этого он ввел функцию распределения f(). Физический смысл этой функции заключается в том, что она позволяет вычислить число молекул dN движущихся со скоростями в интервале (,+d) dN = f()d: f()=4N*(m0/2kT)3/2*U2e(ст.-mU2/2kT),где N-общее число молекул Наиболее вероятная скорость:U=корень из 2kT/m0 Средняя арифметическая скорость:U= корень из 8kT/m0 Средняя квадратичная скорость:U= корень из 3kT/m0 При увеличении температуры интенсивность движения возрастает Согласно молекулярно-кинетической теории – как бы не изменялись скорости отдельных частиц, средняя квадратичная скорость молекулы остается постоянной и равна vкв.Это объясняется тем, что в газе, находящимся в состоянии термодинамического равновесия, устанавливается некоторое стационарное, независящее от времени, распределение молекул по скоростям. Закон распределения молекул по скоростям впервые был выведен Максвелом. При выводе этого закона предполагалось, что газ состоит из состоит из очень большого числа частиц N, которые находятся в состоянии хаотического теплового движения, предполагалось, что никакие силовые поля на частицы газа не действуют., Распределения Больцмана. Основное уравнение МКТ и максвелские распределения молекул по скорости были получены предположением, что молекулы равномерно распределены по объему и все направления движения молекул равномерно распределены по объему и все направления движения молекул равновероятны. Такие условия могут быть реализованы только в том случае, если на молекулы не действуют никакие внешние силовые поля. Однако молекулы любого газа в земных условиях находятся в потенциальном гравитационном поле Земли, что приводит к нарушению равномерного распределения молекул по объему. P = pgh – давление в жидкости ; dP = - pgdh – т.к. с увеличением высоты давление уменьшается. PV = mRT / μ => p = m / V = Pμ / RT ; dP = - Pμ g dh / RT = P m0 g dh / kT ; dP/ P = - m0 g dh / kT ; Проинтегрируем это выражение: (интеграл P0 - P) dP / P = - (m0 g / kT) (интеграл 0 - h) dh ; ln (P / P0) = - (m0 gh / kT) ; P = R0 e (ст. m0 gh / kT) ; P = P0 e (ст. – μ n / RT) ; Это выражение описывает распределение частиц по высоте в гравитационном поле. m0 gh = П, поэтому n = n0 e (ст. – П / kT). Это и есть распределения Больцмана. Оно описывает распределение частиц по высоте в гравитационном поле, а не только в гравитационном поле Земли. Это распределение приемлемо к частицам, находящимся в состоянии заотического теплового движения. 3.3Явление переноса Явление переноса. В термодинамической неравновесной системе возникают особые неравновесные процессы, называемые явлением переноса., в результате которых происходит перенос в пространстве энергии, массы и импульса. К явлениям переноса относятся: 1) теплопроводность (перенос энергии) ; 2) диффузия (перенос массы) ; 3) внутренние трение или вязкость (перенос импульса) ; 1. Теплопроводность-перенос тепла из зоны с большим теплом в зону с меньшим,но не перенос массы! dQ = - æ (dT / dx) S dt ; dS-площадка,dpi/dx-проекция градиента температуры сорта на ось,перпендик-но к dS. æ = 1/3 c p <v> <ЛЯМДА> ; c – теплоемкость, p – плотность. 2.Диффузия – это выравнивание концентраций в смеси нескольких веществ. Этот процес наблюдается в газах, жидкостях и твердых телах. Рассмотрим двухкомпонентную смесь. Будем считать, что молекулы обеих компонент обладают близкими массами и близкими значениями эффективных диаметров. В этом случае можно считать, что |
