ответы на вопросы. 1 Физические свойства жидкостей. Испарение
 Скачать 1.95 Mb. Скачать 1.95 Mb.
|
|
1) Физические свойства жидкостей. Испарение— процесс парообразования, протекающий со свободной поверхности жидкости. Текучесть — смещение слоя жидкости в направление действия внешней силы. Вязкость— способность жидкостей оказывать сопротивление сдвигу ее слоев. Кипение— процесс испарения, протекающий по всему объему жидкости, при этом образуются пузырьки пара. 2) Определение гидростатического давления. Гидростатическое давление— давление столба жидкости, находящейся в состоянии равновесия, над некоторым условно выбранным уровнем при действии силы тяжести.  3) Пьезометрическая высота. Пьезометрическая высота (h)— высота столба данной жидкости, соответствующая данному давлению P (абсолютному или избыточному).  4) Уравнения равновесия Эйлера (в проекциях). 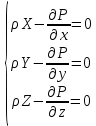 Данные уравнения отражают основные свойства гидростатического давления, другими словами, это давление, действующее на рассматриваемую точку в жидкости одинаково в любом направлении, которое зависит от координат данной точки. 5) Поверхность уровня. Поверхность уровня— поверхность жидкости, любая точка которой имеет одно и тоже значение рассматриваемой функции (функции давления). Уравнение поверхности уровня:  6) Относительное равновесие жидкости в поле силы тяжести. Относительное равновесие жидкости— такое состояние жидкости, при котором каждая ее частица сохраняет свое положение относительно твердой стенки движущегося сосуда, в котором она находится, находящаяся в состоянии покоя. При рассмотрении относительного равновесия жидкости решаются 2 задачи: 1) Определяется форма поверхности уровня (поверхности равного давления). 2) Определяется характер распределения давления на этом уровне. 7) Движение резервуара с жидкостью по вертикали.  Для определения формы поверхности уровня (поверхности равного давления) используют дифференциальное уравнение поверхности: 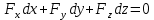 Проекции единичных массовых сил:  Получаем:  Характер распределения давления получаем из основного дифференциального уравнения равновесия: 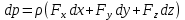 Получаем:  Уравнение показывает, что при движении жидкости по вертикали с полученным уравнением давление изменяется по линейному закону. 8) Горизонтальное перемещение резервуара с жидкостью с постоянным ускорением.  Проекции единичных массовых сил:  Сумма сил:   Уравнение поверхности жидкости:  Закон распределения давления:  Давление также изменяется по линейному закону для любой горизонтальной плоскости при движении сосуда с жидкостью вдоль горизонтальной плоскости с постоянным ускорением a:      9) Давление жидкости на дно цилиндрического сосуда.  В пределах площади дна этого сосуда выделена элементарная площадка  Сила давления на общую площадь дна dp:  Полное гидростатическое давление, действующее на дно сосуда:  Равнодействующая сил давления: 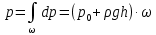 Уравнение показывает, что независимо от формы сосуда, в который налита жидкость и формы его дна, сила гидростатического давления будет одинакова во всех точках и будет определяться только глубиной h и внешним давлением. 10) Давление жидкости на произвольно ориентированную поверхность.     расстояния от точек C и D вдоль рассматриваемой плоскости до свободной поверхности расстояния от точек C и D вдоль рассматриваемой плоскости до свободной поверхностиПолная сила гидростатического давления: 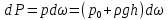 Сила гидростатического давления на свободную поверхность величина постоянная, значит: 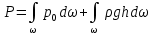   Тогда:  11) Давление жидкости на криволинейные поверхности.  Площадка 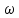 находится в равновесии, система распределенных по ее поверхности сил находится в равновесии, система распределенных по ее поверхности сил  может быть заменена одной равнодействующей силой P: может быть заменена одной равнодействующей силой P: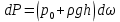  Элементарная сила давления: 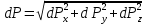  горизонтальные составляющие силы dP, которые действуют вдоль осей Ox и Oy горизонтальные составляющие силы dP, которые действуют вдоль осей Ox и Oy вертикальная составляющая силы dP вертикальная составляющая силы dPГоризонтальные составляющие будут равны:   проекции площадки проекции площадки  на плоскости перпендикулярные плоскостям Ox и Oy на плоскости перпендикулярные плоскостям Ox и OyВертикальная составляющая равна сумме всех элементарных вертикальных составляющих: 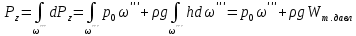  12) Уравнение неразрывности. При течении жидкости должно соблюдаться условие неразрывности изменения параметров потока по координатам и времени. Уравнение неразрывности потока жидкости: 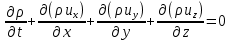 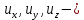 составляющие скорости жидкости вдоль оси x,y,z. составляющие скорости жидкости вдоль оси x,y,z.Если течение установившееся (  : : Если жидкость несжимаемая (капельная), то  : : 13) Формулы компонентов вихря. 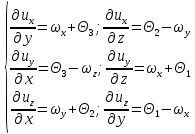 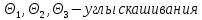   14) Уравнения движения Эйлера для невязкой жидкости. В потоке элементарная частица имеет форму параллелепипеда со сторонами dx,dy,dz. На эту частицу действуют силы гидростатического давления, массовые силы и силы инерции. В проекциях на оси координат можно записать:  15) Уравнения движения невязкой жидкости в форме Громеки-Ламба. Уравнения Громеки-Ламба:  В этих уравнениях ускорения массовых сил являются частными производными частного потенциала U(X,Y,Z):  16) Интегралы Лагранжа и Бернулли. Интеграл Лагранжа: в некотором потенциальном потоке во всех точках сохраняется постоянное значение четырех членов равенства.  Интеграл Бернулли: при установившемся течении жидкости вдоль линии тока должна сохраняться постоянной сумма. 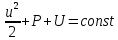 17) Изменение кинетической и потенциальной энергии жидкости при течении вдоль линии тока, отнесенное к единице массы, к единице веса, к единице объема. Изменение кинетической энергии при течении вдоль линии тока: 1) отнесенное к единице массы:  2) отнесенное к единице веса:  3) отнесенное к единице объема:   Изменение потенциальной энергии при течении вдоль линии тока: 1) отнесенное к единице массы:  2) отнесенное к единице веса:  3) отнесенное к единице объема: 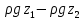 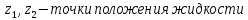 18) Геометрический смысл уравнения Бернулли.  Уравнение Бернулли: 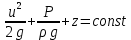 Высота положения (  ) — расстояние от центра тяжести до плоскости OO. ) — расстояние от центра тяжести до плоскости OO.Пьезометрическая высота (  )— расстояние от центра тяжести до плоскости сравнения )— расстояние от центра тяжести до плоскости сравнения  Скоростная высота (  )— расстояние от плоскости сравнения )— расстояние от плоскости сравнения  до плоскости до плоскости  19) Уравнение Бернулли для потока вязкой жидкости. Должны соблюдаться условия: 1. Течение жидкости должно быть плавно изменяющимся. 2. Нормальные к вектору скорости, ускорения будут иметь минимальные или пренебрежительно малые значения по сравнению с продольными составляющими ускорения. 3. Живые сечения должны быть или плоскими, или круглоцилиндрическими. 4. Распределенные гидродинамические давления должны подчиняться гидростатическому закону. Уравнение Бернулли для потока вязкой жидкости: 1. Для единицы массы: 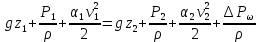 2. Для единицы веса:  3. Для единицы объема:    20) Коэффициент гидравлических сопротивлений. Коэффициент гидравлических сопротивлений (λ) — является функцией числа Рейнольдса и коэф. относительной шероховатости. 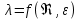  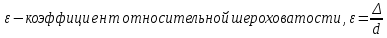 Коэффициент гидравлических сопротивлений вычисляется по следующим правилам: 1. Если течение жидкости ламинарное, т.е. когда  , то λ рассчитывается по формуле Стокса: , то λ рассчитывается по формуле Стокса: 2. Если число Рейнольдса лежит в пределе от 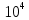 до до  , то λ рассчитывается по формуле Блазиуса(режим течения в гидравлически гладких трубах): , то λ рассчитывается по формуле Блазиуса(режим течения в гидравлически гладких трубах): 3. Если  , то λ рассчитывается по формуле Шифрисона: , то λ рассчитывается по формуле Шифрисона: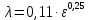 4. Если число Рейнольдса чуть больше 2320 (  ), то λ можно рассчитать с помощью формулы Альтшуля: ), то λ можно рассчитать с помощью формулы Альтшуля: |
