ЛЕКЦИЯ 03. 3. 1 Закон действующих масс. Константа химического равновесия

• Название: 3. 1 Закон действующих масс. Константа химического равновесия
• Анкор: ЛЕКЦИЯ 03.doc
• Дата: 04.03.2018
• Размер: 345 Kb.
• Имя файла: ЛЕКЦИЯ 03.doc
• Тип: Закон; #16226

ЛЕКЦИЯ 3

Термодинамика химического равновесия. Константа химического равновесия. Закон действующих масс. Принцип Ле-Шателье. Изотерма химической реакции. Равновесие в гетерогенных реакциях. Влияние температуры на химическое равновесие. Уравнения изобары и изохоры химической реакции.
3.1 Закон действующих масс. Константа химического равновесия.

Cуществуют реакции, протекающие в двух противоположных направлениях, которые называются обратимыми

Н_{2 газ} + I_{2 газ} 2 НI_газ

С течением времени скорость (V) прямой реакции, которая пропорциональна произведению концентраций исходных веществ, будет уменьшаться, так как уменьшаются концентрации исходных веществ (Н₂ и I₂), а скорость обратной реакции, которая пропорциональна концентрации НI в квадрате, увеличивается, так как увеличивается концентрация НI. Наконец, наступит такой момент, когда V_прямой = V_{обратной}, т. е. наступает состояние химического равновесия.

Устойчивые равновесия (в том числе и химические) характеризуются следующими общими признаками:

1. Неизменностью равновесного состояния системы при сохранении внешних условий.

2. Подвижностью равновесия

3. Динамическим характером равновесия, т.е. установлением и сохранением его вследствие равенства скоростей прямого и обратного процессов.

4. Возможностью подхода к состоянию равновесия с двух противоположных сторон (т.е. вводя только исходные вещества, либо только продукты реакции).

5. Минимальным значением G (или F или соответствующим экстремальным значением другой характеристической функции при иных путях проведения процесса).

Можно вывести конкретные условия равновесия, одним из которых является закон действующих масс (закон действия масс), который был выведен кинетическим способом Гульдбергом и Вааге в 1867 г. (кинетический метод менее строгий, чем термодинамический).

Кинетический вывод закона действующих масс.

Рассмотрим обратимую реакцию:

Н_{2 газ} + I_{2 газ} 2 НI_газ

Для прямой реакции при постоянной температуре скорость реакции равна:

V_прямой = k₁

Для обратной реакции скорость равна:

V_{обратной} = k₂с²_HI

Это математическая форма записи так называемого основного постулата химической кинетики. Здесь k₁ и k₂ – константы скорости прямой и обратной реакции.

При равновесии: V_прямой = V_{обратной}, т.е

. ,

откуда или ,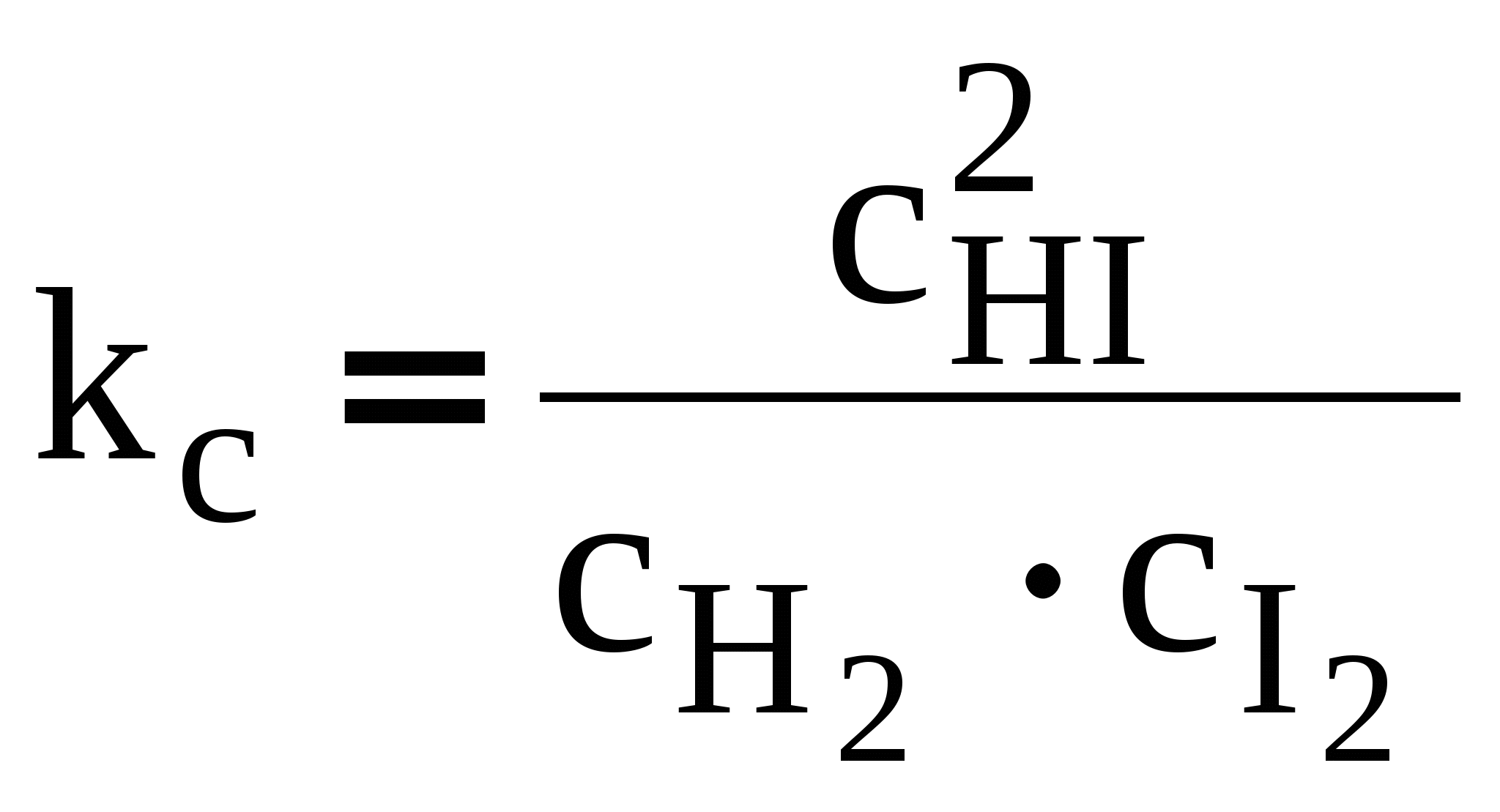

где .

Здесь k_с – константа равновесия, выраженная через равновесные концентрации (ее иногда называют классической константой равновесия или концентрационной константой равновесия). Это и есть математическое выражение закона действующих масс для рассмотренной реакции, который формулируется следующим образом:

отношение произведения равновесных концентраций (или парциальных давлений) продуктов реакции, взятых в степенях, равных их стехиометрическим коэффициентам, к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная для данной реакции.
Термодинамическая константа равновесия.

Химические реакции обратимы и могут протекать как в прямом так и в обратном направлении.

В случае реальных систем равновесные концентрации заменяют на равновесные активности (а_i) и получают термодинамическую константу химического равновесия:

,

где _i – стехиометрические коэффициенты уравнения реакции. Величины положительны для продуктов реакции и отрицательны для исходных веществ.

Константы химического равновесия, выраженные через равновесные парциальные давления р_i или равновесные фугитивности f_i участников реакции, имеют вид: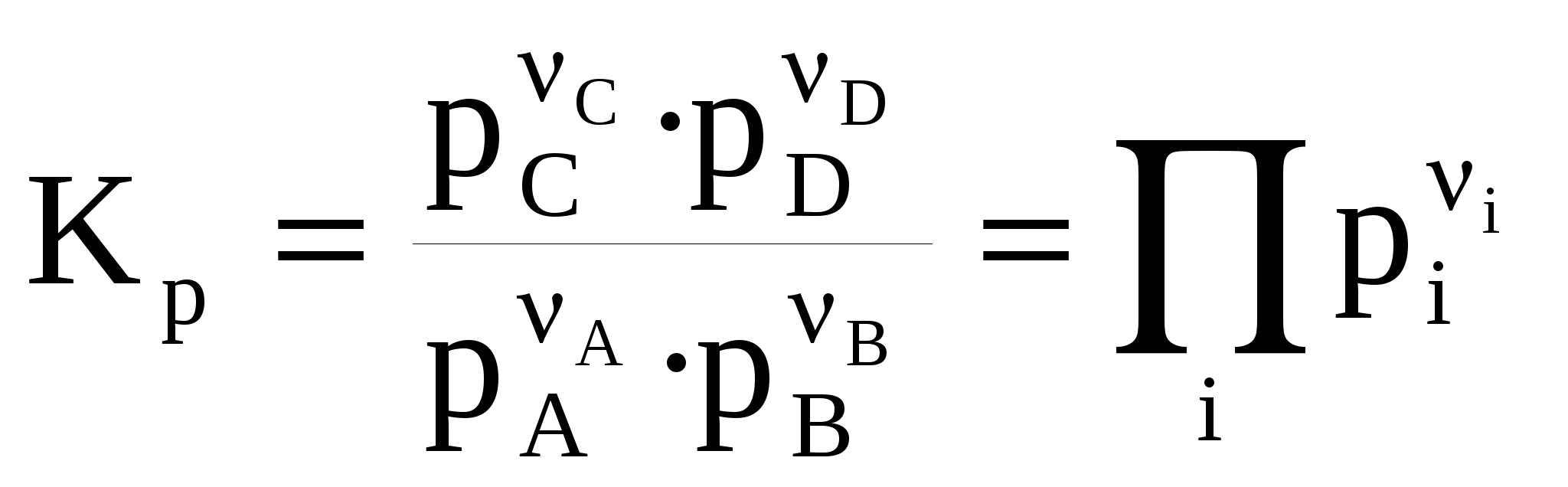

,

.

Один из важных выводов из закона действия масс является взаимосвязь парциальных давлений (или концентраций) всех веществ, участвующих в реакции. В условиях равновесия парциальные давления (или концентрации) всех веществ, участвующих в реакции, связаны между собой. Нельзя изменить парциальное давление (или концентрации) ни одного из них, без изменения парциальных давлений (или концентраций) всех остальных веществ, участвующих в реакции, чтобы сохранилось прежнее численное значение константы равновесия при данных условиях.

Пример 3.1 Процесс получения хлора окислением хлористого водорода протекает по уравнению:

.

При смешении 1 моль HCl с 0,48 моль O₂ образуется 0,402 моль Cl₂. В системе P = 1 атм (1,013*10⁵ Па), T =659 K. Найти значение K_P.

Решение. На образование 0.402 моль Cl₂ расходуется 0.804 моль HCl и 0,201 моль O₂. При установлении в системе равновесия имеем:



Найдем равновесные парциальные давления участников реакции:



Рассчитаем константу равновесия реакции: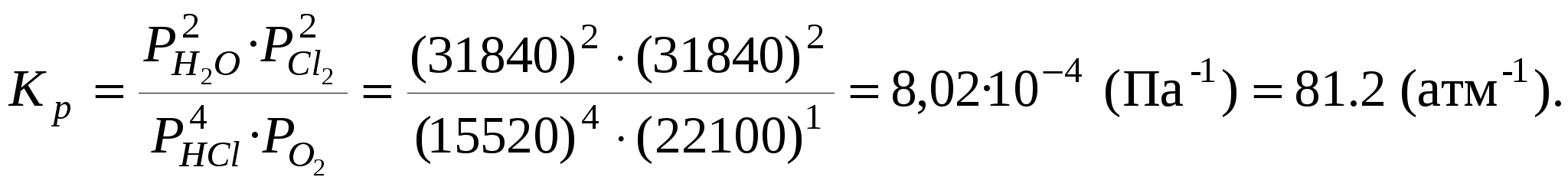


3.2 Условия равновесия для химической реакции.

Рассмотрим реакцию: N_{2 газ} + 3 Н_{2 газ} 2 NН_{3 газ} протекающую при р, Т = const. Изменения количеств веществ в результате химической реакции связаны между собой. Пусть изменение числа молей N₂ будет –0,2 моль; тогда изменение чисел молей (n ) Н₂ и NH₃, будет, соответственно –30,2-0,6 и 20,2=0,4моль. Таким образом видно, что

Но отношения будут одинаковыми для всех участников реакции.
= = = = 0,2

При этом принято, что _i  0 – для продуктов реакции, _i  0 – для исходных веществ.

Величина называется степенью полноты протекания реакции, химической переменной или числом пробегов реакции.

Для любой химической реакции:

, (1)

где (ξ– химическая переменная).

Можно показать, что если _i = сonst (т.е. если состав системы не меняется), то после интегрирования уравнения (1) получается



(_i  0 – для продуктов, _i  0 – для исходных веществ).

Для одного пробега реакции, т.е. в случае, когда ξ = 1 (когда прореагировали вещества в количествах, равных их стехиометрическим коэффициентам: n_i = _i), в условиях постоянного состава системы (в условиях бесконечно большого количества всех компонентов, когда химический потенциал _i = сonst) изменение энергии Гиббса равно:

или



Проанализируем последнее выражение.

1. 
   Если G  0, то
   

(2)

В этом случае реакция может протекать самопроизвольно слева направо при постоянных температуре и давлении.

2. 
   Пусть G  0, тогда
   

(3)

В этом случае реакция может протекать самопроизвольно справа налево при постоянных температуре и давлении.

3. 
   Пусть G = 0, тогда
   

(4)

Система находится в состоянии равновесия.

Условия (2–4) – условия направленности и равновесия процессов для любой химической реакции.

Стандартные условия протекания реакции.

В термодинамике под стандартными условиями понимают, что начальные активности всех компонентов a_i равны единице, т.е. все a_i = 1 (в случае идеальных газов это будет, когда все р_i = 1 атм), причем начальные количества веществ будут настолько велики (бесконечно большие), что их изменение в результате протекания 1 пробега химической реакции не скажется на изменении состава исходной смеси, т.е. на протяжении реакции активности всех компонентов останутся постоянными и равными единице.

Тогда _i = _i⁰ (поскольку _i = _i⁰ + RT lna_i). В результате получим:

(5)

(_i  0 – для продуктов, _i  0 – для исходных веществ).

При равновесии будем иметь:

, (6)

G⁰ – стандартное изменение энергии Гиббса в результате одного пробега химической реакции, протекающей при описанных выше стандартных условиях, (причем не тогда, когда р_общ. = 1 атм, а когда р_i всех участников реакции равны 1 атм и постоянны).
3.3 Изотерма химической реакции.

Уравнение изотермы (или просто изотерма) химической реакции позволяет связать возможное направление химической реакции с исходным составом реагирующих веществ. Уравнение изотермы химической реакции легко получить, используя следующие соотношения:



_i = _i⁰ + RTlna_i, (7)

где а_i – начальная активность i-ого компонента.

(8)

Но ;

поэтому .

В уравнении изотермы химической реакции единицы измерения R = 8,314 , [G] = [G⁰] = Дж.

Здесь G – изменение энергии Гиббса для одного пробега реакции при заданных температуре и давлении и постоянном составе системы (когда количества всех веществ взяты бесконечно большими и их начальные активности заданы равными a_i)

G⁰ – стандартное изменение энергии Гиббса для одного пробега той же реакции, если начальные активности равны единице.

Если задать начальные активности каждого из участников реакции равными их соответствующим равновесным активностям, то система (реакция) будет находиться в состоянии равновесия, поэтому G = 0, и из уравнения изотермы получим: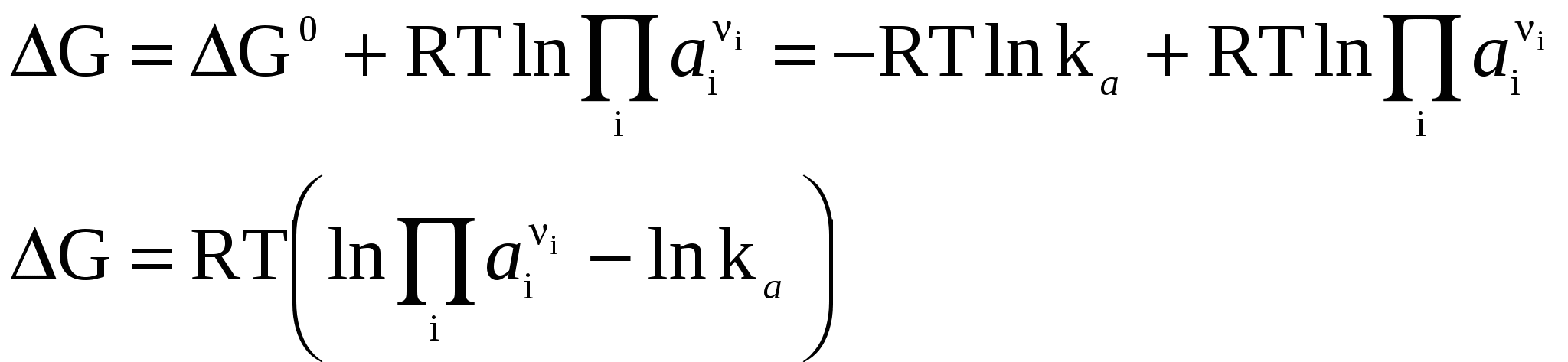

(9)

где (10)

или (11)

(здесь _i  0 – для продуктов, _i  0 – для исходных веществ).

G⁰ = –RT lnk_a (12)



тогда (13)

Для процессов, протекающих при постоянных объеме и температуре, можно получить аналогичное выражение для энергии Гельмгольца, подставив вместо a_i концентрацию с_i:

(14)

где (15)

По уравнению изотермы химической реакции (11) с учетом соотношения (13) можно определить направление протекания химической реакции при заданных начальных концентрациях (парциальных давлениях) участников реакции и, например, при постоянных давлении и температуре.

Рассмотрим уравнение изотермы химической реакции в виде:

, (16)

Может быть три случая:

1) . Следовательно G < 0. В системе термодинамически возможно самопроизвольное протекание прямой реакции при указанных выше условиях.

2) . Следовательно G > 0. В этом случае термодинамически возможно самопроизвольное протекание обратной реакции.

3) . Следовательно G = 0. Данная система будет находиться в состоянии химического равновесия.

Из анализа уравнения изотермы химической реакции видно, что, меняя начальные концентрации (парциальные давления) веществ, в принципе, можно менять и направление протекания реакции.

Иногда в качестве критерия приближенной оценки возможности протекания реакции используют не величину G, а величину G⁰, которую можно рассчитать на основании термодинамических характеристик участников реакции:

G⁰_Т = ⁰_Т – ТS⁰_T;

⁰_T = ⁰₂₉₈ + С⁰_р, 298 (Т – 298); (17)

S⁰_T = S⁰₂₉₈ + С⁰_р, 298 ln. (18)

3.4 Связь между k_р и k_с.

Если рассматривать обратимую газовую реакцию и считать газы идеальными, то выполняются следующие соотношения:

1) Закон Менделеева–Клапейрона pV = nRT (или p_iV = n_iRT).

, где , (19)

Отсюда можно получить следующие соотношения, показывающие взаимосвязь между k_р и k_с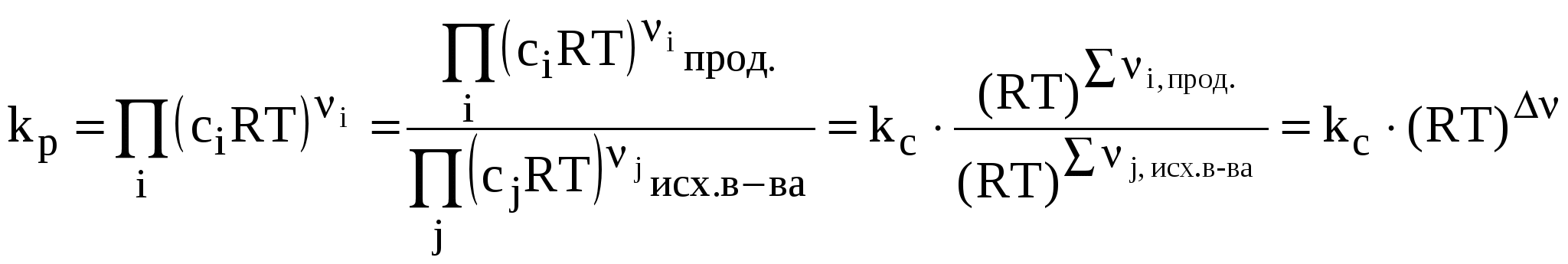

, но т.к. p_i = c_iRT, то получим:

.

Здесь  – изменение числа молей газообразных веществ в результате протекания одного пробега данной реакции. (20)

k_р = k_с (RT)^. (21)

Если парциальные давления компонентов выражены в атмосферах, а концентрации в , то в соотношение, (21) связывающее k_р и k_с, вместо R следует ставить величину R = 0,082 .

k_р не зависит от давления и концентрации, k_с не зависит от концентрации и от давления.

3.5 Равновесие в гетерогенных реакциях.

До сих пор речь шла о гомогенных реакциях (протекающих в одной фазе). Рассмотрим гетерогенные реакции, в которых не все вещества находятся в газообразном состоянии. В случае гетерогенных систем, в которых жидкие или твёрдые вещества не образуют растворов друг с другом и с газообразными веществами, химические потенциалы этих конденсированных веществ при постоянной температуре будут постоянными, также как и давление насыщенных паров над каждым из таких веществ в смеси. Поэтому в выражения для констант равновесия входят давления только газообразных веществ.

СаО_тв. + СО_{2 газ} СаСО_{3 тв.} (22)



В случае, если в гетерогенной реакции принимают участие растворы, в выражения для констант равновесия будут входить активности (концентрации) этих веществ.
3.6 Принцип Ле-Шателье.

Как отмечалось ранее, химические равновесия являются динамичными и подвижными. При изменении внешних условий может происходить сдвиг равновесияв сторону образования либо продуктов реакции, либо исходных веществ. Впервые принцип смещения равновесия сформулировал А. Ле-Шателье.

Принцип Ле–Шателье: если на систему, находящуюся в равновесии, оказывать внешнее воздействие, то равновесие смещается в сторону того процесса, который уменьшает это воздействие.

Теоретически этот принцип был выдвинут Ф. Брауном и теперь известен, как принцип Ле-Шателье – Брауна.

Обычно в качестве внешних факторов, влияющих на состояние равновесия, рассматривают влияние температуры, давления и изменения концентрации реагирующих веществ. Например, с повышением температуры равновесие смещается в сторону эндотермической реакции, протекающей с поглощением теплоты. Уменьшение давления приводит к смещению равновесия в сторону реакции, протекающей с увеличением числа молей газообразных веществ.

Пример 3.2 Рассмотрим реакцию

()

1. 
   Увеличим температуру: так как реакция экзотермическая, т. е. идёт с выделением тепла, равновеие смещается в сторону исходных веществ (обратная реакция идёт с поглощением тепла).
   
2. 
   Увеличим давление: так как прямая реакция идёт с уменьшением числа молей газобразных веществ (т.е. объем уменьшается), то равновесие смещается в сторону продуктов реакции.
   

3.7 Влияние температуры на константу химического равновесия.

Уравнение изобары Вант-Гоффа.

Количественно влияние температуры на константу равновесия выражается с помощью уравнения изобары Вант-Гоффа (р = const) или уравнения изохоры Вант-Гоффа (V = const). Для вывода уравнения изобары Вант-Гоффаз из уравнения

(23)

найдем частную производную от G по Т при р = const: (24)

Это получено, исходя из того, что начальная активность веществ не зависит от температуры, тогда:

() то . (25)

Подставляем в уравнение Гиббса-Гемгольца

значения G и из (23) и (25) соответственно

После преобразований имеем

. (26)

После преобразований имеем

(27)

Здесь Н – тепловой эффект реакции при p = const.

Уравнение (27)– это уравнение изобары Вант-Гоффа в дифференциальной форме. Это уравнение показывает, как константа равновесия k_a зависит от температуры.

Аналогичным способом, рассматривая F вместо G в соответствующих уравнениях типа (23) и (24), можно получить выражение для уравнения изохоры Вант-Гоффа в дифференциальной форме.



Здесь U – изменение внутренней энергии (т.е. тепловой эффект реакции при V = const).

Если рассматривать газофазную реакцию, то для идеальных газов можно записать и тогда

(28)

Рассмотрим случай, когда реакция проводится в стандартном состоянии при р = 1 атм, тогда уравнение (28) примет следующий вид:

(29)

Рассмотрим, как изменяется k_p с изменением температуры. Проанализируем соотношение (29) (здесь H⁰ – тепловой эффект соответствующей химической реакции в стандартном состоянии.

Возможны три случая.

1) H⁰ > 0 – эндотермическая реакция, протекающая с поглощением теплоты. Так как R > 0; T² > 0, тогда, . Известно, что если производная функции (у) , то у – возрастающая функция (т.е. с возрастанием аргумента ее значение увеличивается, а с уменьшением – уменьшается), тогда при увеличении температуры (dT > 0) величина lnk_p, а, следовательно, и k_p, возрастает, а при уменьшении температуры k_p уменьшается.

2) H⁰ < 0 – экзотермическая реакция, протекающая с выделением теплоты.

; тогда , следовательно, функция lnk_p убывающая, то есть с ростом аргумента -температуры величина lnk_p а, значит, и k_p, уменьшается.

3) H⁰ = 0; . Функция lnk_p (а также и k_p) не зависит от температуры, то есть k_p – постоянная при Т  сonst.

Зависимость k_p (или k_p) от температуры может иметь следующий вид:




1. H⁰₁ = 0

2. H⁰₂ > 0

3. H⁰₃ < 0
Для получения интегральной формы уравнения изобары Вант-Гоффа нужно соответствующую дифференциальную форму проинтегрировать, для чего в уравнении (29) разделим переменные:

. (30)

Вычислим неопределенный интеграл:

. (31)

Если H⁰ не зависит от температуры, то

(32)

(где А – некоторая константа).

Возьмем теперь определенный интеграл:

(33)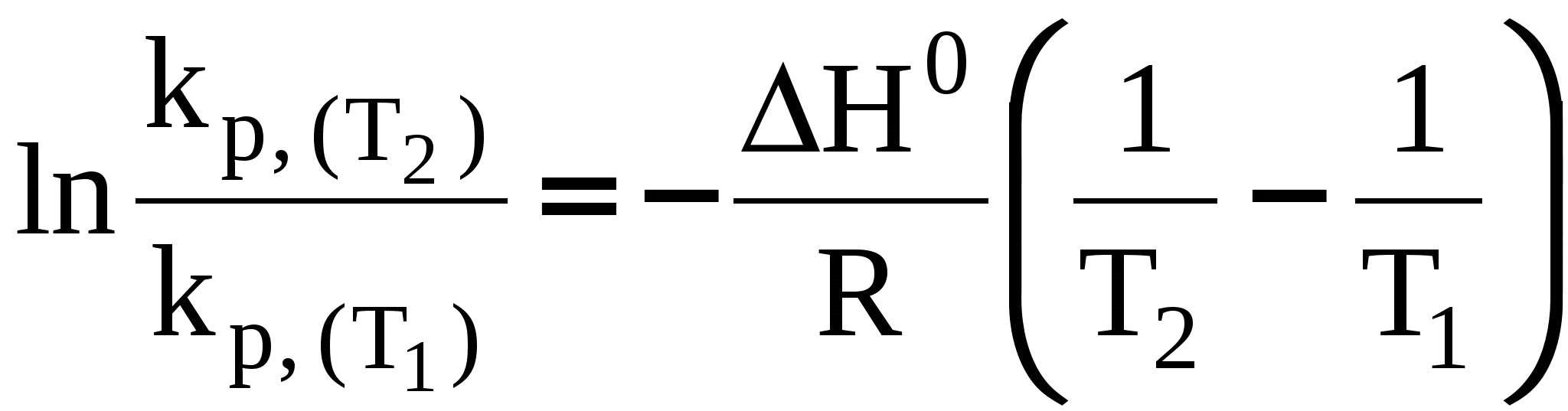

или

(34)

Таким образом, зная значения константы равновесия ( и ) при двух температурах (Т₁ и Т₂), можно рассчитать величину теплового эффекта реакции H⁰ или же, зная величину H⁰ и значение константы равновесия при какой-либо температуре Т₁, можно определить k_p при другой температуре Т₂.

Из уравнения (32) видно, что, зная зависимость k_p от Т, можно графически определить величину теплового эффекта химической реакции. Надо провести линеаризацию соответствующего уравнения (т.е. осуществить выбор соответствующих координат, чтобы получить прямую линию: y = lnk_p; x =).

1. 
   ₁⁰ < 0 (c ростом Т величина lnk_p убывает);
   
2. 
   ₂⁰ = 0;
   
3. 
   ₃⁰ > 0 ( c ростом Т величина lnk_p возрастает).
   

Из графика можно рассчитать величину теплового эффекта реакции:

и .