Шпоры Дунюшкин 2012. 1. Физикохимические свойства пластовой нефти. Условные компоненты пластовой нефти. Молярный объём нефти, примеры
 Скачать 1.8 Mb. Скачать 1.8 Mb.
|
Определение потерь напора на трениеПотеря напора на преодоление трения hT по длине трубопровода круглого сечения при любом режиме течения определяется по формуле Дарси-Вейсбаха: 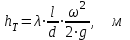 Из (69) следует, что 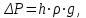 Тогда потери давления будут 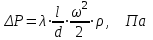 Если скорость выразить через объемный расход и площадь сечения 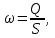 то уравнение примет вид: 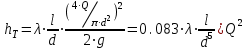 В наклонном трубопроводе: 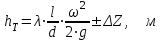 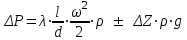 + - когда сумма участков подъема по высоте больше суммы участков спуска; - - когда наоборот. где l – длина трубопровода, м; d- внутренний диаметр, м; ρ- плотность жидкости, кг/м3; ΔZ- разность геодезических отметок начала и конца трубопровода, м; g- ускорение силы тяжести, м/с2; λ- коэффициент гидравлического сопротивления, который в общем случае зависит от числа Рейнольдса Re и относительной шероховатости стенки трубопровода 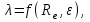 где ε– относительная шероховатость где ε– относительная шероховатость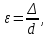 где Δ– абсолютная эквивалентная шероховатость выбирается по таблице, мм; d- внутренний диаметр трубы, мм. где Δ– абсолютная эквивалентная шероховатость выбирается по таблице, мм; d- внутренний диаметр трубы, мм.Абсолютная эквивалентная шероховатость – это такая высота шероховатости, при которой в квадратичной зоне сопротивления потери напора равны потерям напора для данной естественной шероховатости трубы. Для ламинарного режима движения (Rе < Rекр) коэффициент гидравлического сопротивления зависит только от параметра Рейнольдса: Rекр = 2320 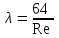 Если учесть, что Если учесть, что 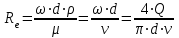 и подставить выражение (79) в (78), то получим и подставить выражение (79) в (78), то получим 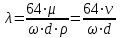 В этом случае выражение принимает вид формулы Пуазейля:  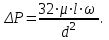 При турбулентном режиме движения (Rе > Rекр) различают три зоны сопротивления. Зона гидравлически гладких труб ( 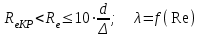 ): ):  -формула Блазиуса, используемая при Rе ≤105. Здесь сопротивление шероховатых и гладких труб одинаково. -формула Блазиуса, используемая при Rе ≤105. Здесь сопротивление шероховатых и гладких труб одинаково.В зависимости от скорости течения и вязкости жидкости одна и та же труба может быть гидравлически гладкой и гидравлически шероховатой. 2. Зона шероховатых труб или смешанного трения (  ): ):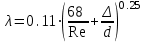 - формула Альтшуля. - формула Альтшуля.3. Зона вполне шероховатых труб или квадратичная зона ( 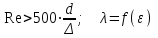 ): ):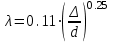 - формула Шифринсона. - формула Шифринсона.Для нефтепроводов наиболее характерны режимы гладкого или смешанного трения. Определение потерь напора на местные сопротивления(для сложных трубопроводов)Местными сопротивлениями называются участки трубопровода, в которых происходит резкая деформация потока (к ним относятся, в частности, все виды арматуры трубопроводов – вентили, задвижки, тройники, колена и т.д.). Потери напора в местных сопротивлениях hM определяются по формуле Вейсбаха (в долях скоростного напора) 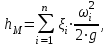 где n– число местных сопротивлений; ω- средняя скорость потока за местным сопротивлением; ξ- коэффициент местного сопротивления, зависящий от его геометрической формы, состояния внутренней поверхности и Re, а для запорных устройств - от степени их открытия. При развитом турбулентном движении (Re > 104), что соответствует квадратичной зоне сопротивления для местных сопротивлений, ξКВ = const и определяется по справочникам. где n– число местных сопротивлений; ω- средняя скорость потока за местным сопротивлением; ξ- коэффициент местного сопротивления, зависящий от его геометрической формы, состояния внутренней поверхности и Re, а для запорных устройств - от степени их открытия. При развитом турбулентном движении (Re > 104), что соответствует квадратичной зоне сопротивления для местных сопротивлений, ξКВ = const и определяется по справочникам.Потери напора в местных сопротивлениях можно рассчитать по формуле Дарси-Вейсбаха через эквивалентную длину lэкв, понимая под ней такую длину трубопровода, для которой hT = hM.  где lП– приведенная длина трубопровода где lП– приведенная длина трубопровода 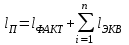 Обычно зона деформации потока в районе местного сопротивления мала по сравнению с длиной труб. Поэтому в большинстве задач принимается, что потери напора в местном сопротивлении происходят как бы в одном сечении, а не на участке, имеющем некоторую длину. Таким образом, полный перепад давления с учетом местных сопротивлений и рельефа местности определяется из формулы: 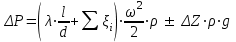 При больших длинах напорных трубопроводов удельный вес местных сопротивлений невелик и ими при расчетах пренебрегают. При движении жидкости по трубопроводу происходит потеря давления по его длине, вызываемая гидравлическими сопротивлениями. Величина потерь давления (напора) зависит от диаметра трубопровода, состояния его внутренней поверхности (гладкая, шероховатая), количества перекачиваемой жидкости и ее физических свойств. Зависимость между путевой потерей напора и расходом жидкости, то есть hП = f(Q) называется гидравлической характеристикой трубопровода. 8. Гидравлические расчёты простых трубопроводов при изотермическом движении по ним нефтяного газа При движении нефтяного газа по трубопроводу происходит значительное падение давления по длине в результате преодоления гидравлических сопротивлений. В этих условиях плотность газа уменьшается, а линейная скорость – увеличивается. Установившееся изотермическое (Т=const) движение газа в газопроводе описывается системой трех уравнений: Уравнение Бернулли: dP/gг + d/2g + dz + *dx/d * 2/2g = 0 (1) Уравнение состояния: P =г*Rг*T*z, (2); где Rг = R/M (3) 3. Закон сохранения массы: G = г*s = cons (4) При этом следует помнить, что изотермический процесс описывается уравнением Бойля-Мариотта: Р/ = const (5) При выводе расчетной формулы вторым и третьим слагаемыми в уравнении (1) пренебрегают, т.к. считают, что увеличения линейных скоростей в газопроводе не происходит и газопровод проложен горизонтально. При этих допущениях уравнение (1) запишется в виде: -dP/gг = *dx/d * 2/2g = 0 Определим из (4) линейную скорость и подставим получаем: -dP/gг = *dx/d *G2/2gS2г2 Умножив левую и правую части на г2 и сократив g, получим: -г*dP = *dx/d *G2/2S2 Из (129) выразим г и подставим в последнее выражение, получим: -PdP/z RгT = *dx/d * G2/2S2 = 0 Возьмем интеграл от данного уравнения в пределах от начального давления Р1 до конечного Р2 в газопроводе длиной от 0 до L: -1/zRгTР2Р1PdP = * G2/2dS2L0dx Подставив вместо площади величину S = d2/4, получим окончательно: P12 – P22/2 z RгT = * 16 G2 L / 2 2d5 Или _________________ G = d2/4(P12 – P22)d/zRгTL , кг/с Формула (138) является основной для расчета массового расхода газа по трубопроводу. Для гидравлических гладких труб не зависит от шероховатости внутренней поверхности трубы и рассчитывается по формуле: =0.067(158/Re)0.2=0.1844/ Re0.2 При квадратичном режиме течения , и является функцией относительной шероховатости: =0.067(2/d)0.2 По универсальной формуле ВНИИ газа: =0.067(158/Re+2/d)0.2 Значение числа Re для смеси газов: 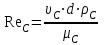 , где С=у11+ у22+…+ уnn – вязкость смеси газов; С – плотность смеси газов в условиях трубопровода, кг/м3. , где С=у11+ у22+…+ уnn – вязкость смеси газов; С – плотность смеси газов в условиях трубопровода, кг/м3.Обычно течение газа происходит при высоких скоростях, когда сопротивление определяется только шероховатостью труб (квадратичная зона). Т.к. шероховатость не зависит от диаметра трубопровода, можно считать, что зависит только от диаметра газопровода. Одной из формул типа = (d), получившей широкое распространение, является формула Веймаута: =0.009407/ 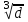 Формула Веймаута может использоваться при ориентировочных расчетах диаметра и пропускной способности простого газопровода. Формула Веймаута может использоваться при ориентировочных расчетах диаметра и пропускной способности простого газопровода. 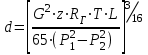 ; ;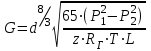 . . Из формулы (142) можно получить выражение для определения длины L, диаметра d и конечного давления Р2 при известном начальном Р1: 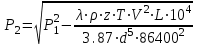 . . Гидравлические расчеты сложных трубопроводов при изотермическом движении по ним нефтяного газа. Запишем систему уравнений для потока нефтяного газа в трубопроводе: 1. 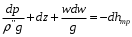 2. 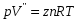 3. 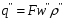 В практических расчетах можно пренебречь влиянием разности отметок крайних точек газопровода и изменением линейной скорости газа. Потери на трение определяются по уравнению Дарси-Вейсбаха: 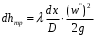 Тогда получим: 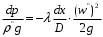 Т.к. 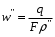 , подставляя это выражение в предыдущее, получим: , подставляя это выражение в предыдущее, получим: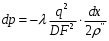 Т.к. 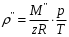 , подставляя в предыдущее, получим дифференциальное уравнение связи всех интересующих нас параметров: , подставляя в предыдущее, получим дифференциальное уравнение связи всех интересующих нас параметров: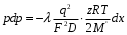 Интегрируя полученное выражение получим: 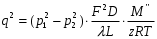 Значение коэффициента гидравлического сопротивления  рассчитывают в зависимости от режима движения газа и шероховатости труб. рассчитывают в зависимости от режима движения газа и шероховатости труб.Одной из формул типа 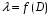 , получившей широкое распространение, является формула Веймаута: , получившей широкое распространение, является формула Веймаута: 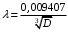 Формулу Веймаута можно использовать при ориентировочных расчетах диаметра или пропускной способности простого газопровода. В этом случае расчетные формулы имеют вид: 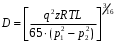 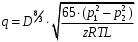 Иногда для увеличения надежности работы газосборной сети прокладывают две или несколько параллельных ниток. Пропускная способность всей серии газопроводов:  Пропускная способность газопровода переменного диаметра: 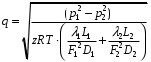 Существуют газовые коллекторы трех типов: линейный, лучевой и кольцевой. Линейный и каждую нитку лучевого коллектора рассчитывают следующим образом: 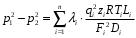 Если газопровод на всех участках выполнен из труб одного диаметра, то расчетная формула имеет вид: 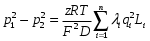 9. Распределение температуры по длине неизотермического трубопровода. Вывод формулы Шухова В. Г. П 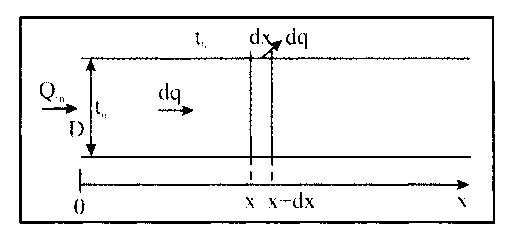 усть по трубопроводу диаметром Dдвижется однофазная продукция с массовым расходом q. Температура продукции на входе в трубопровод tH. Температура окружающей среды to. Поток стационарный, то есть распределение температуры по длине трубопровода во времени не меняется. Из этого следует, что все тепло, которое выделяется при охлаждении продукции уходит в окружающую среду. Удельная теплоемкость потока сри коэффициент теплоотдачи КоТ. Трубопровод горизонтальный. Введем систему координат, ось х. Составим баланс тепловой энергии на элементе трубопровода dx. усть по трубопроводу диаметром Dдвижется однофазная продукция с массовым расходом q. Температура продукции на входе в трубопровод tH. Температура окружающей среды to. Поток стационарный, то есть распределение температуры по длине трубопровода во времени не меняется. Из этого следует, что все тепло, которое выделяется при охлаждении продукции уходит в окружающую среду. Удельная теплоемкость потока сри коэффициент теплоотдачи КоТ. Трубопровод горизонтальный. Введем систему координат, ось х. Составим баланс тепловой энергии на элементе трубопровода dx.Где Следовательно Проинтегрируем полученное уравнение: откуда 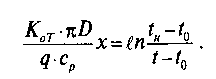 Обозначим Тогда следует формула ВТ. Шухова для расчета распределения температуры по длине трубопровода 10. Типичные структуры газонефтяных потоков в горизонтальных и наклонных трубопроводах [по Гужову А.И. - ?] Структурная форма газожидкостного потока — это пространственное распределение потоков жидкой и газовой фаз в трубопроводе. В зависимости от формирующейся в трубопроводе структуры потока меняется его гидравлическое сопротивление из-за изменений: формы поверхности раздела фаз, характера взаимодействия фаз между собой и стенками трубопровода и, как следствие, относительной скорости движения сосуществующих фаз. Структурные формы газожидкостных потоков весьма разнообразны и зависят от: скорости движения смеси; объемного соотношения фаз в трубопроводе; физических свойств жидкой и газовой фаз; межфазного поверхностного натяжения; диаметра и угла наклона трубопровода; направления потока в отдельных участках рельефного трубопровода.  А.И. Гужовым и учениками его школы в Грозненском нефтяном институте были выделены следующие шестьструктурных форм движения воздуховодяной смеси (рис. 3.2). При раздельно-волновой форме потока с ростом скорости движения газожидкостной смеси на поверхности жидкости развиваются гравитационные волны в направлении движения смеси, что вызывает некоторую пульсацию давления в трубопроводе. Размеры волн и пульсация давления с увеличением скорости смеси возрастают и раздельно-волновая структура потока переходит в пробковую. Пузырьковая форма газожидкостного потока наблюдается при небольших газосодержаниях и характеризуется движением окклюдированного газа в виде пузырей в верхней части сечения трубы при почти полном отсутствии пульсации давления. Размеры основного числа пузырей примерно одинаковы, а скорость их движения не больше средней скорости смеси. С увеличением скорости смеси происходит дробление пузырей, а при скорости более 0,2 м/с окклюдированные газовые пузырьки равномерно распределяются в жидкости. Рост газосодержания в смеси при прочих равных условиях вызывает коалесценцию (слияние) пузырьков газа, приводя к возникновению более крупных газовых скоплений. При скоростях менее 0,2 м/с слияние пузырьков газа приводит к образованию непрерывной газовой фазы, т.е. формированию раздельной структуры потока. При более высоких скоростях газожидкостной смеси коалесценция пузырей газа приводит к образованию газовых пробок. Пробковая структура газожидкостного потока характеризуется последовательным чередованием газовых и жидкостных пробок. С увеличением газосодержания размеры газовых пробок увеличиваются, а жидкостных уменьшаются. При дальнейшем увеличении газосодержания жидкостные пробки переходят в волны и поток становится раздельно-волновым. С увеличением скорости происходит разрушение (в зависимости от газосодержания) газовых или жидкостных пробок. При низких объемных расходных газосодержаниях 30% об. и меньше разрушаются газовые пробки с образованием вначале пузырей, затем эмульсионной однородной структуры. При более высоких газосодержаниях происходит разрушение верхней части жидкостных пробок с обильным образованием пены с последующей сменой структурной формы потока на проб-ково-диспергированную, для которой характерно пульсирующее движение газовых пробок, разделенных небольшими диспергированными жидкостными перемычками. Такой режим течения характеризуется наибольшими пульсаииями давленияс периодическим затормаживанием потока, прорывом и слиянием газовых скоплений. Увеличение скорости смеси приводит к уменьшению высоты волн, увеличению распыленной жидкости из-за разрушения пены и сопровождается уменьшением пульсации давления. Дальнейшее увеличение скорости еще больше разрушает газовые и жидкостные скопления. При объемных расходных газосодержаниях до 70% наиболее интенсивно разрушаются газовые скопления, и поток переходит в эмульсионную форму. При более высоких газосодержаниях преимущественно разрушаются волновые жидкостные скопления с образованием жидкой дисперсионной среды. На стенках трубопровода по всему его периметру образуется устойчивый слой жидкости, то есть возникает новая пленочно-диспергированная (кольцевая) форма газожидкостного потока. В пленочно-диспергированном состоянии часть жидкости движется в виде мельчайших капель в ядре потока, остальная часть в виде пленки на стенке трубы, образуя кольцо, толщина которого в нижней части больше, чем в верхней. При очень больших расходах газа практически вся жидкость переходит в распыленное состояние, и поток становится ярко выраженным диспергированным. При газосодержаниях более 95—98% об. раздельно-волновая структура потока непосредственно переходит в пробково-диспергированную или пленочно-диспергированную. При небольшом содержании жидкости в потоке жидкостные пробки не возникают. Образующиеся волны разрушаются, не успевая перекрыть сечение трубы. Области существования структурных форм потока в значительной мере зависят от: направления потока и угла наклона трубы. Например, при восходящем течении отсутствует раздельно-волновая структура и, как следствие, значительно расширяется область пробковой структуры газожидкостного потока. При нисходящем движении наблюдаются такие же структурные формы течения газожидкостной смеси, как и при горизонтальном, но граница перехода раздельно-волновой формы потока в пробковую смещается в сторону больших скоростей смеси с увеличением угла наклона трубы. Основными факторами, определяющими границы существования структурных форм являются: скорость смеси и объемное расходное газосодержание в ней. С увеличением диаметра трубопровода область раздельно-волновой формы потока расширяется, а пузырьково-пробковой сокращается. Остальные структурные формы потока по существу не зависят от диаметра трубопровода. Существенное влияние на структурные формы потока оказывают свойства жидкости. Повышение вязкости жидкости и снижение межфазного поверхностного натяжения вызывает более интенсивное дробление газовых пузырей и пенообразование при одновременном уменьшении относительной скорости фаз и затухании волн. Поток становится более однородным независимо от его структуры. Повышение разности плотностей жидкости и газовой фазы увеличивает их гравитационное разделение. Таким образом, структурные формы газонефтяных потокови границы их существования могутсущественно отличатся от таковых для водовоздушных смесей. Экспериментальные промысловые исследования на месторождениях Чечено-Ингушетии позволили установить следующие структурные формы течения газонефтяной смеси в горизонтальных и наклонных трубах: раздельно-волновая (раздельная); пробково-эмульсионная (пробковая); пленочно-диспергированная и эмульсионная. В отличие от движения водовоздушных смесей газонефтяные потоки скважинной продукции имеютследующие специфические особенности: При снижении давления по длине трубопровода происходит непрерывное образование газовой фазы в нефти в виде мельчайших пузырьков. Устойчивость образующейся газонефтяной эмульсии благодаря естественным ПАВ, содержащимся в нефти, и высокое газосодержание нефти, непрерывно увеличивающееся с возрастанием скорости смеси. Образование устойчивых пен, способствующих насыщению газовой фазы нефтью. В определенных условиях пенная структура потокаможет иметь преобладающее значение. В газонефтяных потоках не происходит полного гравитационного разделения фаз, что обуславливает особенности структурных форм и закономерностей изменения: истинного газосодержания потока, пульсаций давления и других гидравлических характеристик потока. В промысловых трубопроводах могут одновременно сосуществовать различного характера эмульсии и пены. Влияние диаметра труб проявляется в том, что с его увеличением граница перехода раздельной структуры в пробковую смещается в сторону больших скоростей. Однако темп этого изменения уменьшается и в трубах относительно большого диаметра (более 0,2 м) ста новится практически мало заметным. С увеличением давления и снижением межфазного поверхностного натяжения величина скорости смеси, при которой раздельное течение переходит в пробковое уменьшается.   Наибольшую область распространения как по скорости смеси, так и по газосодержанию имеют пробковая и эмульсионная структуры потока. Наибольшую область распространения как по скорости смеси, так и по газосодержанию имеют пробковая и эмульсионная структуры потока.Область пленочно-диспергированного (кольцевого) течения существует при скоростях более 8-10 м/с и объемном расходном газосодержании более 85%. Границы существования пленочно-диспергированной и эмульсионной структур потока мало зависят от диаметра труб и определяются в основном степенью турбулизации потока и свойствами сосуществующих фаз. Области существования пленочно-диспергированной и эмульсионной форм как в восходящем, так и нисходящем потоке примерно такие же, как при горизонтальном течении. Для промысловых нефтегазопроводов пробковая и эмульсионная структуры являются наиболее распространенными формами течения смеси. Между отдельными формами газонефтяного потока фактически нет четких границ раздела — имеются сравнительно широкие переходные зоны как по скорости, так и по газосодержанию. В промысловых трубопроводах под влиянием рельефа местности обуславливается сравнительно частое изменение направления потока и, как следствие, изменение структурных форм потока. |
