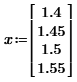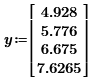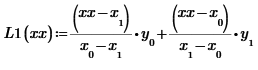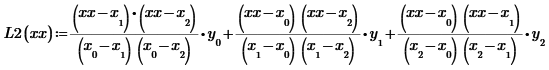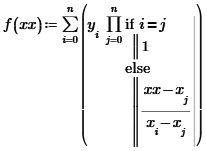Главная страница
Навигация по странице:

  • 2. Точка интерполяции для формулы Ньютона a = 0.22. Выбор и нумерация узлов.

  • Номера выбранных узлов (k) x

  • заданной точностью, добавлять узлы вправо

  • Ручной расчет по 1–й формуле Лагранжа.

  • Степень многочлена k Pk(x) Погрешность

  • 2.8. Решение задачи интерполяции с использованием средств пакета MathCad .

  • 2.9 Решение задачи интерполяции с использованием средств пакета Scilab .

  • _a_=_-3.6541216_-2.0296255_5.3997127">--> ans = -2.8335994 --> "Квадратичная интерполяция" --> a = -3.6541216 -2.0296255 5.3997127

  • 2.0148941 ans = -2.8367423

  • 2.9 Решение задачи интерполяции с использованием средств пакета C ++.

  • Вывод.

    		•

    1. Индивидуальное задание. Точка интерполяции для формулы Ньютона a 22. Выбор и нумерация узлов


    Скачать 202.85 Kb.
    Название1. Индивидуальное задание. Точка интерполяции для формулы Ньютона a 22. Выбор и нумерация узлов
    Дата08.03.2022
    Размер202.85 Kb.
    Формат файлаdocx
    Имя файла2.docx
    ТипДокументы
    #386668

    1.Индивидуальное задание.






    2. Точка интерполяции для формулы Ньютона a = 0.22.

    Выбор и нумерация узлов.

    Для ручной интерполяции в точке x = b = 1.49 по 1 формуле Лагранжа выбираем 4 узла из таблицы 2–2 так, чтобы точка b = 1.49 оказалась между узлами с номерами с 1 по 2 и добавляем узлы вправо:



    Номера выбранных узлов (k)

    xk

    yk

    27
    1.40
    4.9280

    28
    1.45
    5.7760

    29
    1.50
    6.6750

    30
    1.55
    7.6265

    Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке по 1 формуле Лагранжа, с заданной точностью,

    добавлять узлы вправо относительно точки x=a.

    Изменим нумерацию узлом интерполяции для использования их в интерполяционных формулах и занесем в таблицы вида 2–3

    K
    0
    1
    2
    3

    xk
    1.40
    1.45
    1.50
    1.55

    yk
    4.9280
    5.7760
    6.6750
    7.6265



    Ручной расчет по 1–й формуле Лагранжа.

    Заполним таблицу конечных разностей:

    x
    y
    Δy
    Δ2y
    Δ3y

    0.2
    -4.0240
    0,074
    0,0268
    0,0019

    0.25
    -3.9500
    0,2628
    0,0287



    0.3
    -3.8610
    0,2915






    0.35
    -3.7555











    Запишем 1–ю интерполяционную формулу Ньютона


    для многочленов 1–й, 2–й и 3–й степени и выполним расчеты по ним.

    Определим значение q: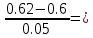

    0.4
    Значение многочлена 1-й степени в т. x=0.12:




    Значение многочлена 2-й степени в т. x=0.12: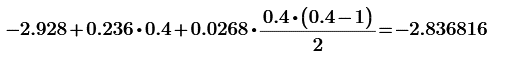





    Значение многочлена 3-й степени в т. x=0.12: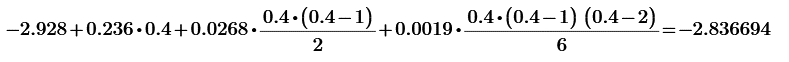





    Важно: Выражения для многочленов 1, 2 и 3 степени могут быть получены после соответствующих преобразований формулы:


    В нашем случае они будут иметь вид:

    P1= -5.7600002 + 4.7200013*x

    P2=-3.6541216 - 2.0296255*x + 5.3997127*x2

    P3=-4.2045571 + 0.5203651*x + 1.4697783*x2 + 2.0148941*x3

    Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для многочленов 1–й и 2–й степени:


    Степень многочлена k
    Pk(x)
    Погрешность

    1
    - 2.8336
    0,003216

    2
    - 2.836816
    0,000122

    3
    - 2.836694





    Вывод. Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в т. а. Оценку погрешности проведём в соответствии с неравенством:



    Можно утверждать, что разность между точным значением функции и значением функции в т.x=0.62 после 3-х итераций не превышает 0.0002.

    2.8. Решение задачи интерполяции с использованием средств пакета MathCad.




    Ручной расчет по формуле Лагранжа


















    Расчет с использованием пакета MathCad

    2.9 Решение задачи интерполяции с использованием средств пакета Scilab.

    -> exec('Интерполяция функции.sce')

    -->

    "Линейная интерполяция"
    --> a =
    -5.7600018

    4.7200028

    --> ans =
    -2.8335994
    -->

    "Квадратичная интерполяция"
    --> a =
    -3.6541216

    -2.0296255

    5.3997127
    --> ans =
    -2.8368398

    "Кубическаяинтерполяция"
    --> a =
    -4.2045571

    0.5203651

    1.4697783

    2.0148941
    ans =
    -2.8367423




    // Линейная интерполяция. 1-я формула Ньютона.

    x=[0.60 0.65]; y=[-2.9280 -2.6920]; z=[x;y]; a=[0;0];

    function [zr]=R(a, z)

    zr=z(2)-a(1)-a(2)*z(1)

    endfunction

    disp('Линейная интерполяция');

    a=datafit(R,z,a)

    deff('y=i1(x)','y=-5.7600002+4.7200013*x');

    i1(0.62)

    //Квадратичнаяинтерполяция

    x=[0.60 0.65 0.70]; y=[-2.9280 -2.6920 -2.4290]; z=[x;y]; a=[0;0;0];

    function [zr2]=R(a, z)

    zr2=z(2)-a(1)-a(2)*z(1)-a(3)*z(1)^2

    endfunction

    disp('Квадратичная интерполяция');

    a=datafit(R,z,a)

    deff('y=i2(x)','y=-3.6541216-2.0296255*x+5.3997127*x^2');

    i2(0.62)

    //Кубическаяинтерполяция

    x=[0.60 0.65 0.70 0.75]; y=[-2.9280 -2.6920 -2.4290 -2.1375];z=[x;y]; a=[0;0;0;0];

    function [zr3]=R(a, z)

    zr3=z(2)-a(1)-a(2)*z(1)-a(3)*z(1)^2-a(4)*z(1)^3

    endfunction

    disp('Кубическаяинтерполяция');

    a=datafit(R,z,a)

    deff('y=i3(x)','y=-4.2045571+0.5203651*x+1.4697783*x^2+2.0148941*x^3');

    i3(0.62) // Интерполяция в точке


    2.9 Решение задачи интерполяции с использованием средств пакета C++.


    // LR2.cpp: главный файл проекта.
    #include "stdafx.h"

    #include

    #include
    using namespace std;
    void x1(float x[])

    {

    x[0] = 1.4;

    x[1]=1.45;

    x[2]=1.5;

    x[3]=1.55;

    }

    void y1(float y[])

    {

    y[0]=4.928;

    y[1]=5.776;

    y[2]=6.675;

    y[3]=7.6265;

    }

    int main(int n, float z)

    {

    float x[4], y[4];

    float s = 1, p = 0, p1, p2, e = 1E-4;

    int k = 1, N = 3;

    z = 1.41;

    p2 = 1;

    x1(x);

    y1(y);

    cout<<"n f(x)"<
    do

    {

    s = 1;

    p = 0;

    n = k;

    for(int i = 0; i <= n; ++i)

    {

    for(int j = 0; j <= n; ++j)

    {

    if (i != j)

    {

    s = s*((z - x[j])/(x[i] - x[j]));

    }

    }

    p = p + y[i]*s;

    s = 1;

    p1 = p2;

    p2 = p;

    }

    cout<

    k++;

    }while((abs(p1 - p) > e)&&(k <=N ));

    system("pause");

    return 0;

    }


    Вывод. Полученные выражения многочленов 1, 2 и 3-ей степени, а также их

    значения в заданной точке b=1.41 совпадают до 4 знака после десятичной точки с ручным расчетом.

    написать администратору сайта