Физика. Задания ч.3. doc. 1. интерференция света основные формулы и законы
 Скачать 1.6 Mb.
|
107 м/с]
107 м/с]Задания 4.1. Определите радиусы первых трех стационарных орбит в атоме водорода. А. [0,53∙10-10 м; 2,12∙10-10 м; 4,77∙10-10 м] B. [4,77∙10-10 м; 0,53∙10-10 м; 2,12∙10-10 м] C. [0,53∙10-10 м; 4,77∙10-10 м; 2,12∙10-10 м] D. [2,12∙10-10 м; 0,53∙10-10 м; 0,75∙10-10 м] 4.2. Определите скорости электрона на первых трех стационарных орбитах. A. [2,19∙106 м/c; 1,1∙106 м/c; 0,73∙106 м/c] B. [3,1∙106 м/c; 5,2∙106 м/c; 7,3∙106 м/c] C. [0,1∙106 м/c; 0,3∙106 м/c; 0,5∙106 м/c] D. [1,0∙106 м/c; 0,7∙106 м/c; 0,4∙106 м/c] 4.3. Определите период обращения электрона на первой стационарной орбите в атоме водорода. A. [1,43∙10-16 c] B. [2,86∙10-16 c] C. [4,86∙10-16 c] D. [5,86∙10-16 c] 4.4. Определите угловую скорость электрона на первой стационарной орбите в атоме водорода. A. [4,4∙1016 рад/c] B. [5,6∙1016 рад/c] C. [6,7∙1016 рад/c] D. [7,8∙1016 рад/c] 4.5. Определите кинетическую, потенциальную и полную энергии электрона на первой стационарной орбите в атоме водорода. A. [21,76∙10-19 Дж; - 43,52∙10-19 Дж; - 21,76∙10-19 Дж] B. [- 21,76∙10-19 Дж; 43,52∙10-19 Дж; 21,76∙10-19 Дж] C. [31,76∙10-19 Дж; 41,75∙10-19 Дж; 53,76∙10-19 Дж] D. [21,76∙10-19 Дж; 43,52∙10-19 Дж; 21,76∙10-19 Дж] 4.6. Определите наибольшую и наименьшую длины волн в серии Лаймана. A. [121,6 нм; 91,2 нм] В. [102,6 нм; 91,2 нм] C. [656,3 нм; 102,6 нм] D. [434,0 нм; 121,6 нм] 4.7. Определите наибольшую и наименьшую частоты волн в серии Бальмера. A. [0,82∙1015 Гц; 0,45∙1015 Гц] В. [3,29∙1015 Гц; 2,46∙1015 Гц] C. [3,29∙1015 Гц; 0,82∙1015 Гц] D. [2,46∙1015 Гц; 0,82∙1015 Гц] 4.8. Определите потенциал ионизации и первый потенциал возбуждения атома водорода. A. [13,6 В; 10,2 В] В. [10,2 В; 13,6 В] C. [21,1 В; 15,3 В] D. [27,2 В; 20,4 В] 4.9. Максимальная длина волны спектральной линии в серии Лаймана равна 0,122 мкм. Полагая, что постоянная Ридберга неизвестна, определите максимальную длину волны в серии Бальмера. A. [0,656 мкм] В. [0,852 мкм] С. [0,102 мкм] D. [0,486 мкм] 4.10. 1). Какую наименьшую энергию (в электронвольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серий спектра водорода? 2). Какую наименьшую скорость должны иметь эти электроны? A. [13,6 эВ; 2,2 ∙106 м/с] В. [10,2 эВ; 1,8 ∙106 м/с] С. [27,2 эВ; 3,1 ∙106 м/с] D. [10,2 эВ; 2,2 ∙106 м/с] 4.11*. Используя теорию Бора, определите орбитальный магнитный момент электрона, движущегося по первой орбите атома водорода. A. [0,93∙10-23 А∙м2] В. [2,8∙10-23 А∙м2] С. [1,8∙10-23 А∙м2] D. [0,45∙10-23 А∙м2] 4.12. Предполагая, что в опыте Франка и Герца вакуумная трубка наполнена не парами ртути, а разреженным атомарным водородом, определите, через какие интервалы ускоряющего потенциала возникнут максимумы на графике зависимости силы анодного тока от ускоряющего потенциала. A. [10,2 В] В. [4,9 В] C. [13,6 В] D. [9,8 В] 4.13*. Атомарный водород освещается ультрафиолетовым излучением с длиной волны 100 нм. Определите, какие спектральные линии появятся в спектре излучения атомарного водорода. A. [λ1,2 = 121,6 нм; λ 1,3 = 102,6 нм; λ 2,3 = 656,3 нм] В. [λ 2,3 = 656,3 нм; λ 2,4 = 486 нм; λ 2,5 = 434 нм] С. [λ 1,2= 121,6 нм; λ 2,3= 656,3 нм; λ 2,4 = 486 нм] D. [λ 1,2 = 121,6 нм; λ 1,3 = 102,6 нм; λ 2,4 = 486 нм] 4.14. В спектре излучения атомарного водорода интервал между двумя линиями, принадлежащими серии Бальмера, составляет 1,71∙10-7 м. Определите с помощью этой величины постоянную Ридберга. 4.15. Основываясь на том, что энергия ионизации атома водорода равна 13,6 эВ, определите в электронвольтах энергию фотона, соответствующую самой длинноволновой линии серии Пашена. A. [0,48 эВ] В. [1,89 эВ] C. [10,2 эВ] D. [6,31 эВ] 4.2. Элементы квантовой механики Основные формулы и законы Длина волны де Бройля  , где  – постоянная Планка,p– импульс частицы.Связь импульса частицы с кинетической энергией Т  ,гдеm – масса частицы. При малых скоростях  .Соотношение неопределенностей Гейзенберга 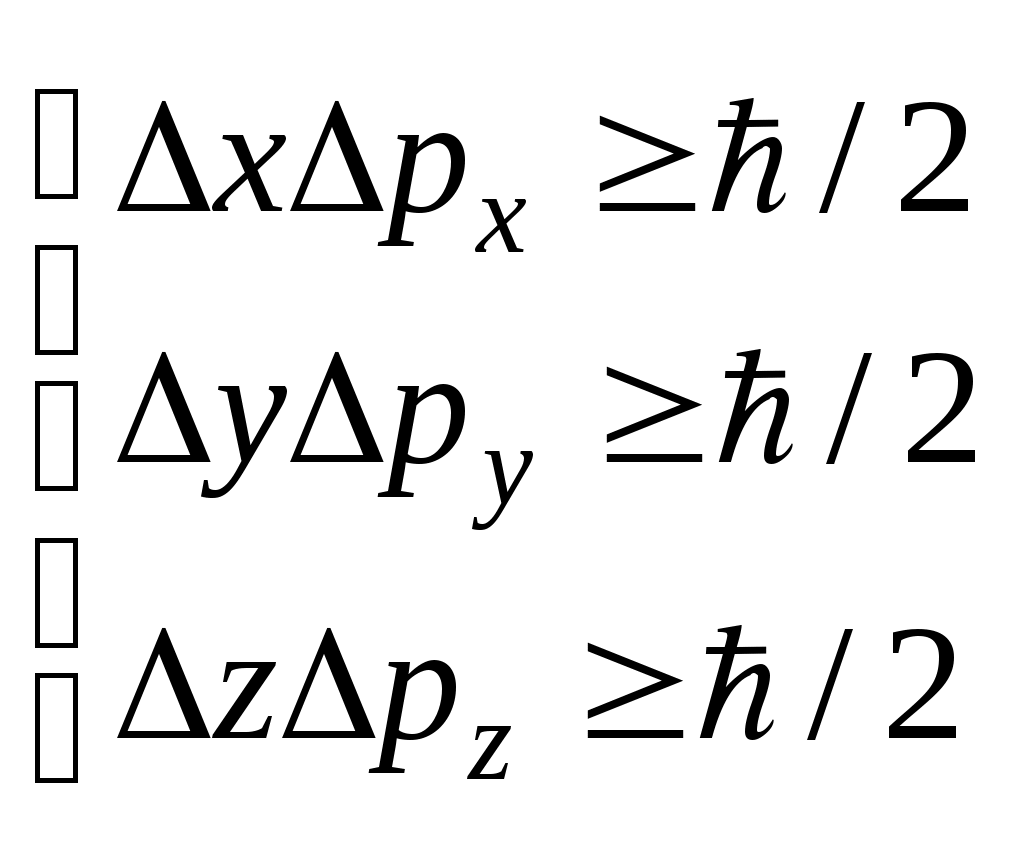  ,где  , - соответственно неопределенности координаты, импульса, энергии и времени, ħ=h/ .Нестационарное уравнение Шредингера  .Уравнение Шредингера для стационарных состояний  , где  – волновая функция микрочастицы,  - полная энергия микрочастицы,  = - потенциальная энергия частицы, - пространственная координата ( =  ), t – время,∆ =  - оператор Лапласа (записан в декартовых координатах), m – масса микрочастицы, ћ – постоянная Планка,  =  - мнимая единица.Одномерное уравнение Шредингера для стационарных состояний  .Условие нормировки волновой функции   .Плотность вероятности   , где dW(x) –вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке dх. Вероятность обнаружения частицы в интервале от х1 до х2 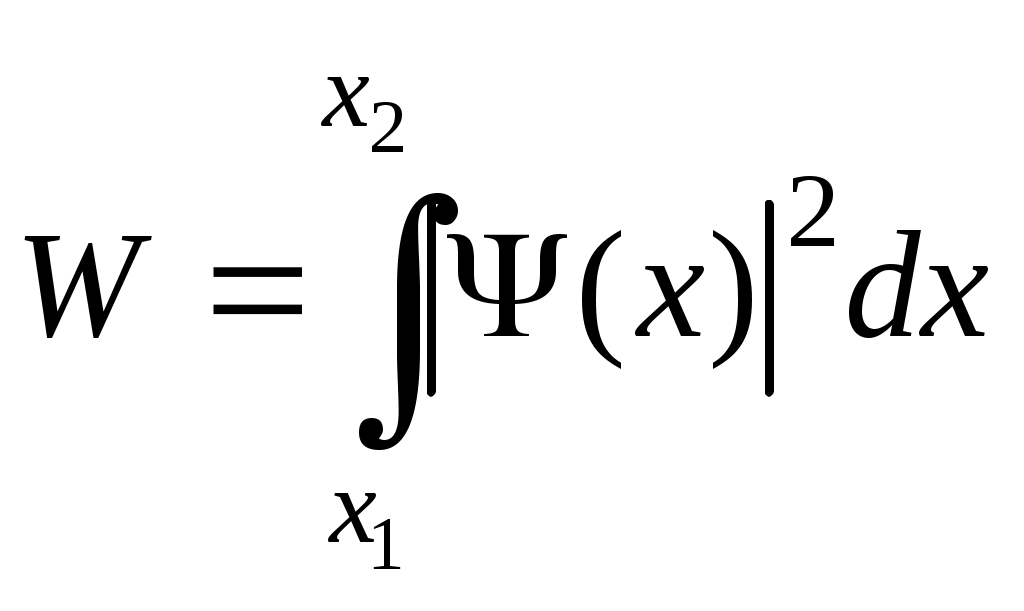 .Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной  (0 ≥ x ≥ ) (собственная нормированная волновая функция) (собственное значение энергии), где n – главное квантовое число ( n = 1, 2, 3,…). В области 0 ≥ x ≥ = ∞ и  = 0. ,где  - коэффициент прозрачности барьера (коэффициент прохождения). Энергия квантового осциллятора  , где n – главное квантовое число ( n = 0, 1, 2,…),  - циклическая чачтота.Для частиц с целочисленными спинами (бозонов) справедлива статистика Бозе-Эйнштейна, а для частиц с полуцелыми спинами (фермионов) справедлива статистика Ферми-Дирака. Обобщенное уравнение для квантовых статистик  ,где  - среднее число частиц в состоянии с номером  , Ei - энергия частицы в этом состоянии; μ – так называемый химический потенциал, определяемый из условия   = Ni, т. е. сумма всех частиц равна полному числу N частиц в системе, знак минус (-) перед единицей в знаменателе соответствует статистике бозонов (распределению Бозе-Эйнштейна, а знак плюс (+) соответствует статистике фермионов (распределению Ферми -Дирака).Задания 4.16. Вычислите длину волны де Бройля для протона, прошедшего разность потенциалов U = 10 В. A. [9,1 пм] В. [91 пм] С. [0,91 пм] D. [4,55 нм] 4.17. При какой скорости электрона дебройлевская длина волны будет равна: а) 500 нм; б) 0,1 нм? (В случае электромагнитных волн первая длина волны соответствует видимой части спектра, вторая – рентгеновским лучам). A. [1,46 ∙103 м/с; 0,73 ∙107 м/с] В. [0,73 ∙103 м/с; 1,46∙107 м/с] С. [2,92 ∙103 м/с; 1,46 ∙107 м/с] D. [1,46 ∙107 м/с; 2,92 ∙103 м/с] 4.18. Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислите длину волны де Бройля для такого электрона. A. [86 пм] В. [43 пм] С. [172 пм] D. [344 пм] 4.19. На грань кристалла никеля падает под углом 64о к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Принимая расстояние между атомными плоскостями кристалла равным 200 пм, определите скорость электронов, если они испытывают дифракционное отражение первого порядка. A. [2 Мм/с] В. [1 Мм/с] С. [0,5 Мм/с] [4 Мм/с] 4.20. Скорость протона составляет (8,880 ± 0,012)∙105 м/с. С какой максимальной точностью можно измерить его положение? A. [13 пм] В. [26 пм] С. [65 пм] D. [40 пм] 4.21. Исходя из того, что радиус атома имеет величину порядка 0,1 нм, оцените скорость движения электрона в атоме водорода. A. [∆  = 5,8 ∙105 м/с; |
С. [∆
= 5,8 ∙104 м/с; 
= 3∙10-9] B. [
, где А – нормировочный коэффициент волновой функции, r – расстояние электрона от ядра, 
– первый боровский радиус. Определите наиболее вероятное расстояние электрона от ядра в основном состоянии. 
] 
, где 
– нормировочный коэффициент волновой функции, r – расстояние этой частицы до силового центра, 
– некоторая постоянная, имеющая размерность длины. Определите среднее расстояние 
частицы от силового центра. 
= 
] В. [
] С. [
] D. [
]