Моделирование и исследование характеристик типовых динамических звеньев систем автоматического управления. Лабораторная 1 (вариант 24). 1 Исследование инерционного звена
 Скачать 1.82 Mb.
|
|
Целью лабораторной работы является получение навыков разработки электронных моделей типовых динамических звеньев САУ, исследование их частотных и переходных характеристик на этих моделях. Такими звеньями, в частности, являются инерционное, инерционное форсирующее, а также звенья второго порядка (колебательное и апериодическое). Данные варианта 24:  4, Т=200 мс.1 Исследование инерционного звена 1.1 Собрать схему модели апериодического (инерционного) звена, установить значения  = = =100 кОм. По формулам  ,  рассчитать параметры остальных элементов в соответствии с данными для индивидуального варианта.1.2 Получить переходную характеристику и определить время переходного процесса  .1.3 Получить экспериментальные ЛАЧХ и ЛФЧХ, замерить частоту среза  и значение фазы  на этой частоте.1.4 Увеличить значения постоянной времени Т звена в два, три и четыре раза и повторить выполнение заданий по п.п. 1.2 и 1.3. 1.5 Построить графики зависимостей  ,  и  .1.6 Оценить влияние величины постоянной времени на характеристики апериодического (инерционного) звена. 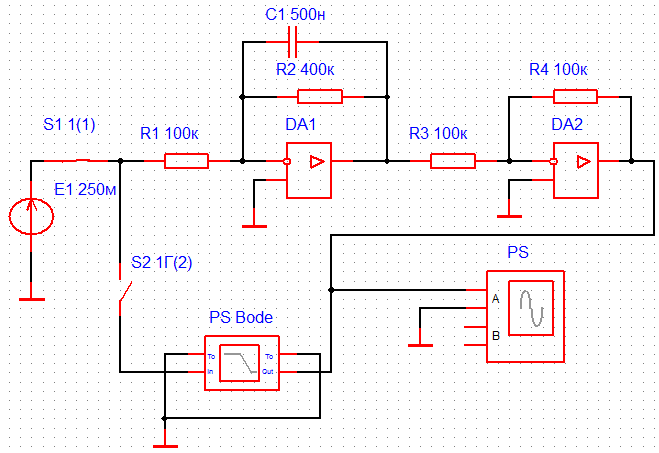 Рисунок 1 – Схема для исследования инерционного звена 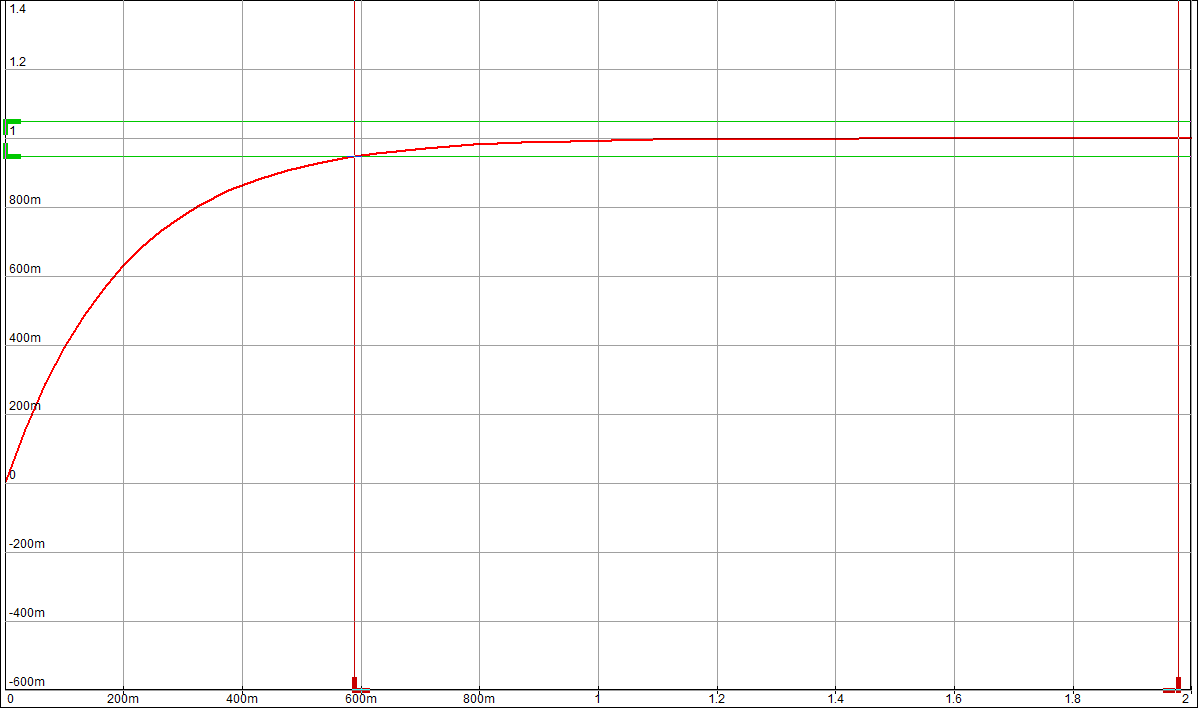 Рисунок 2 – Переходная характеристика инерционного звена (при Т=200 мс) 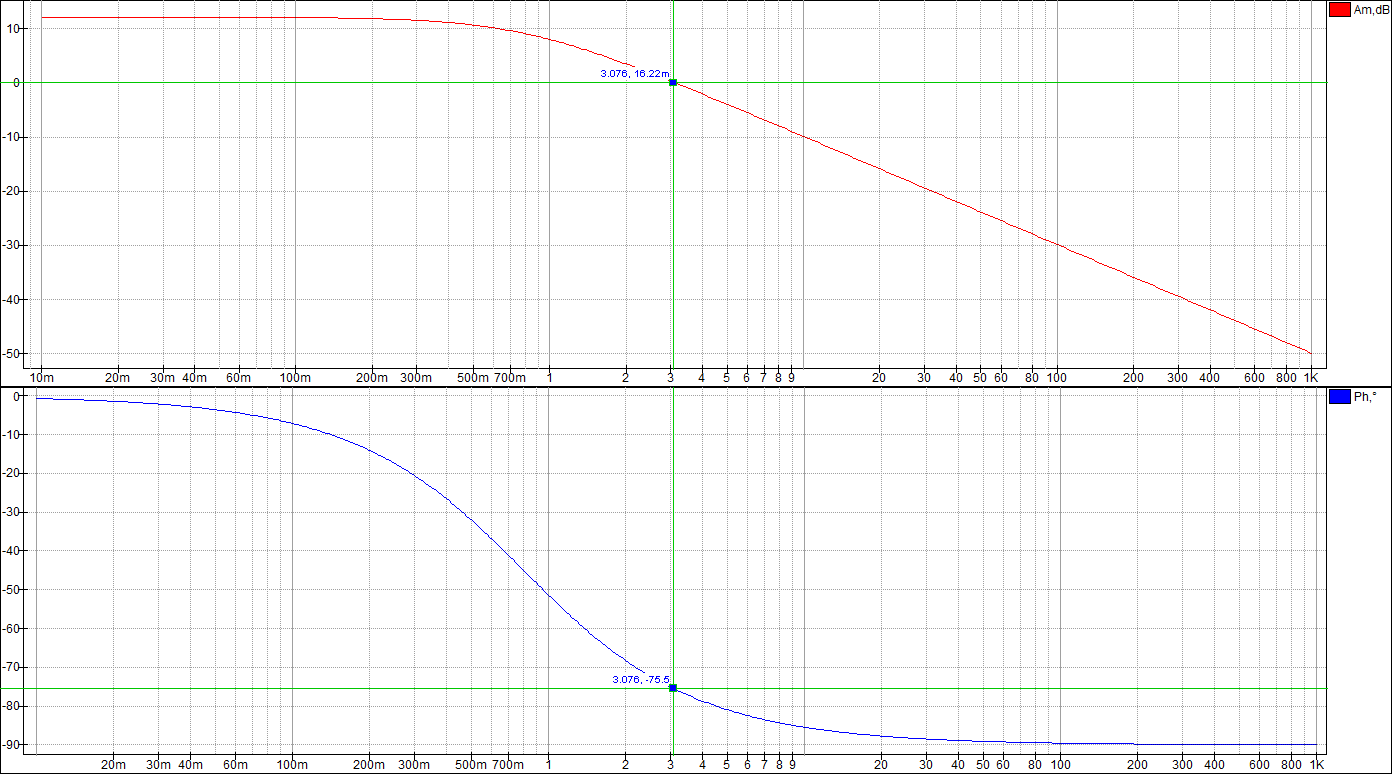 Рисунок 3 – ЛАЧХ и ЛФЧХ инерционного звена (при Т=200 мс) 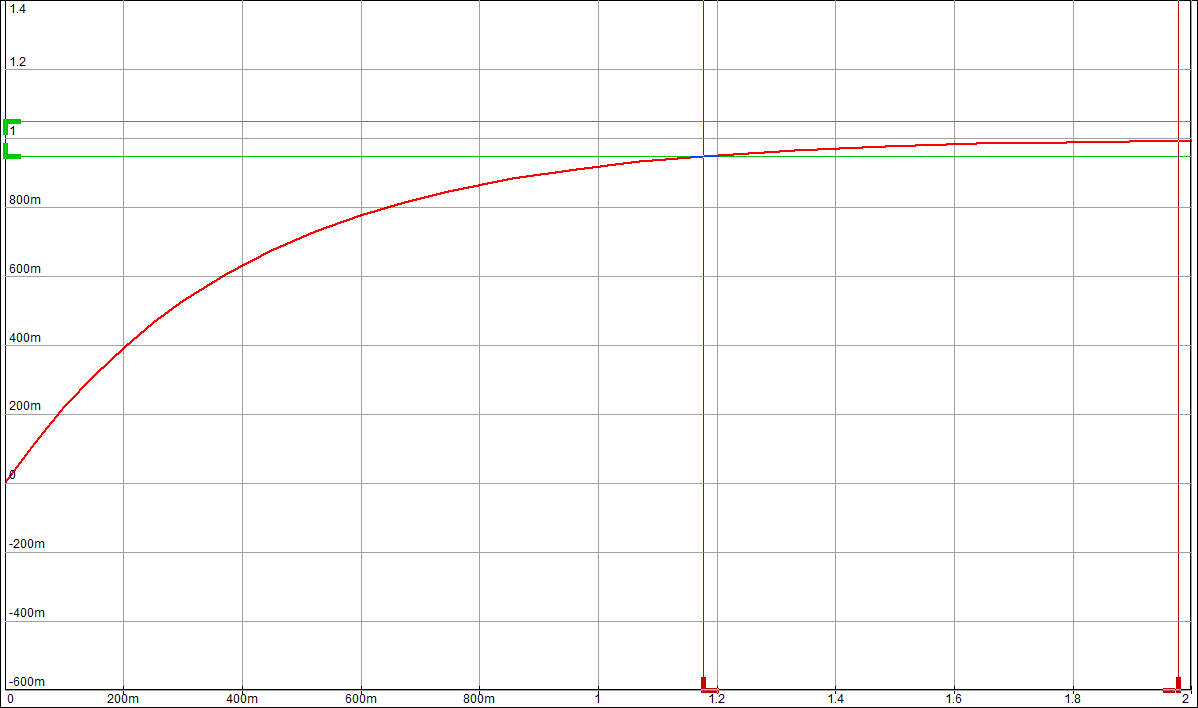 Рисунок 4 – Переходная характеристика инерционного звена (при Т=400 мс) 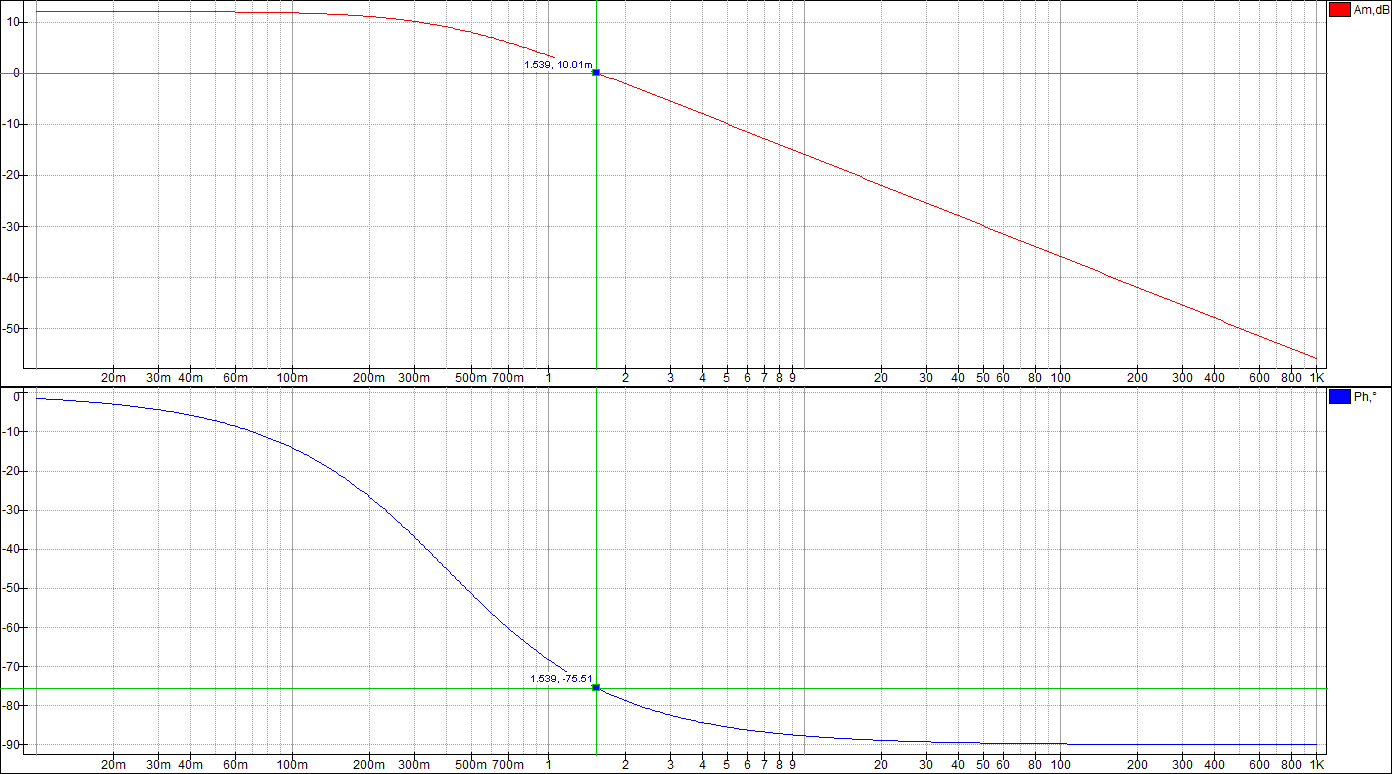 Рисунок 5 – ЛАЧХ и ЛФЧХ инерционного звена (при Т=400 мс) 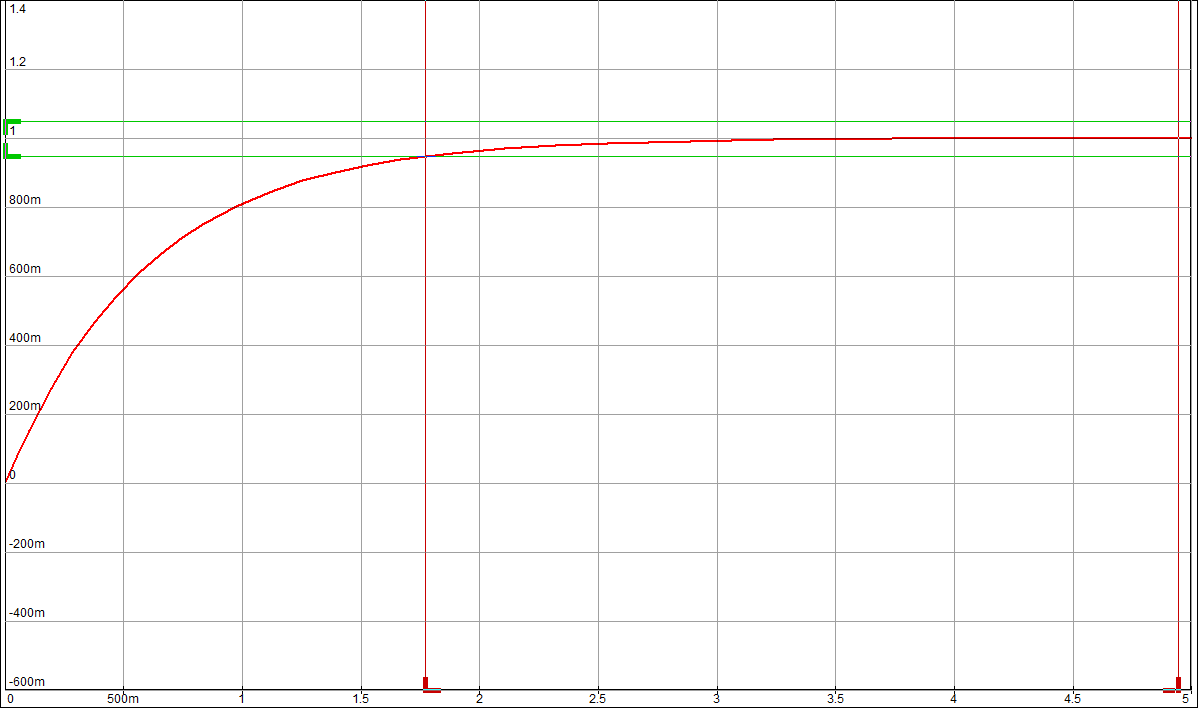 Рисунок 6 – Переходная характеристика инерционного звена (при Т=600 мс) 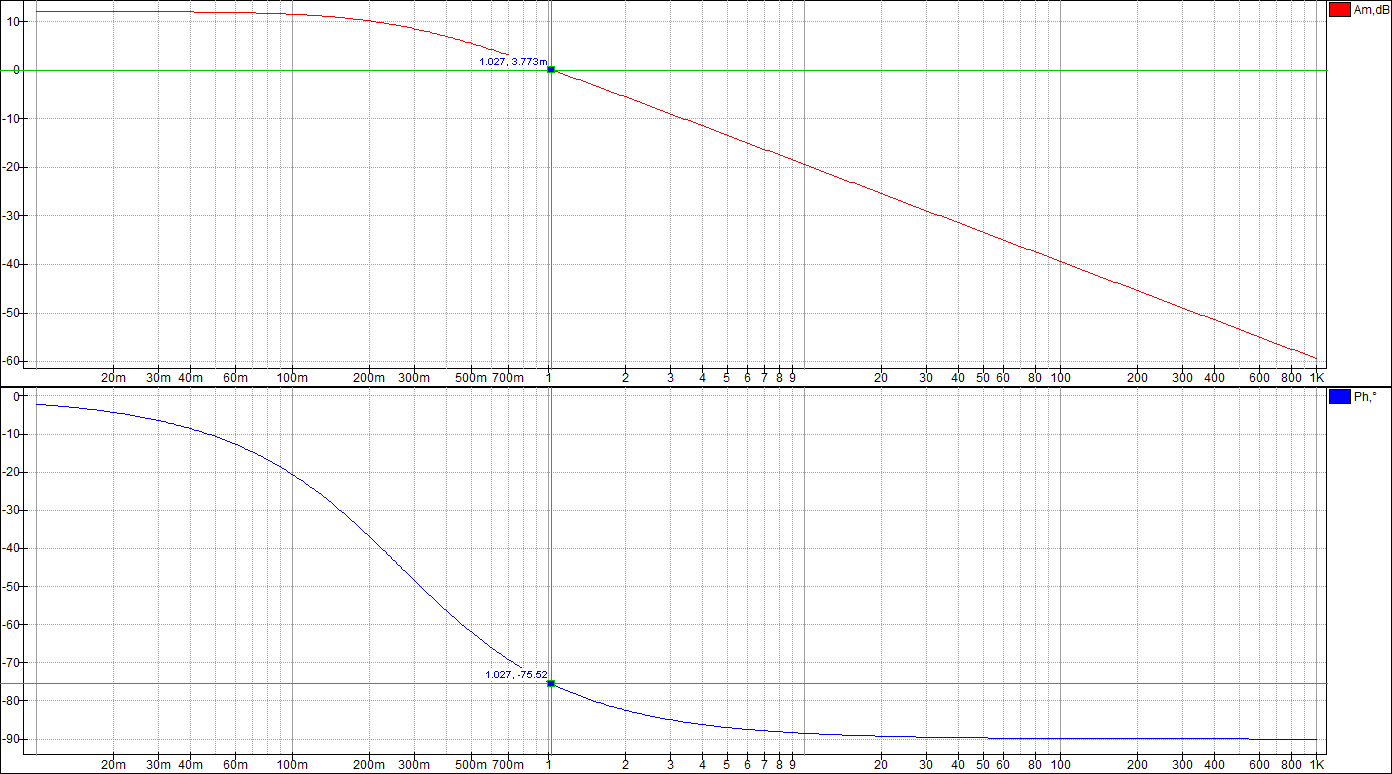 Рисунок 7 – ЛАЧХ и ЛФЧХ инерционного звена (при Т=600 мс) 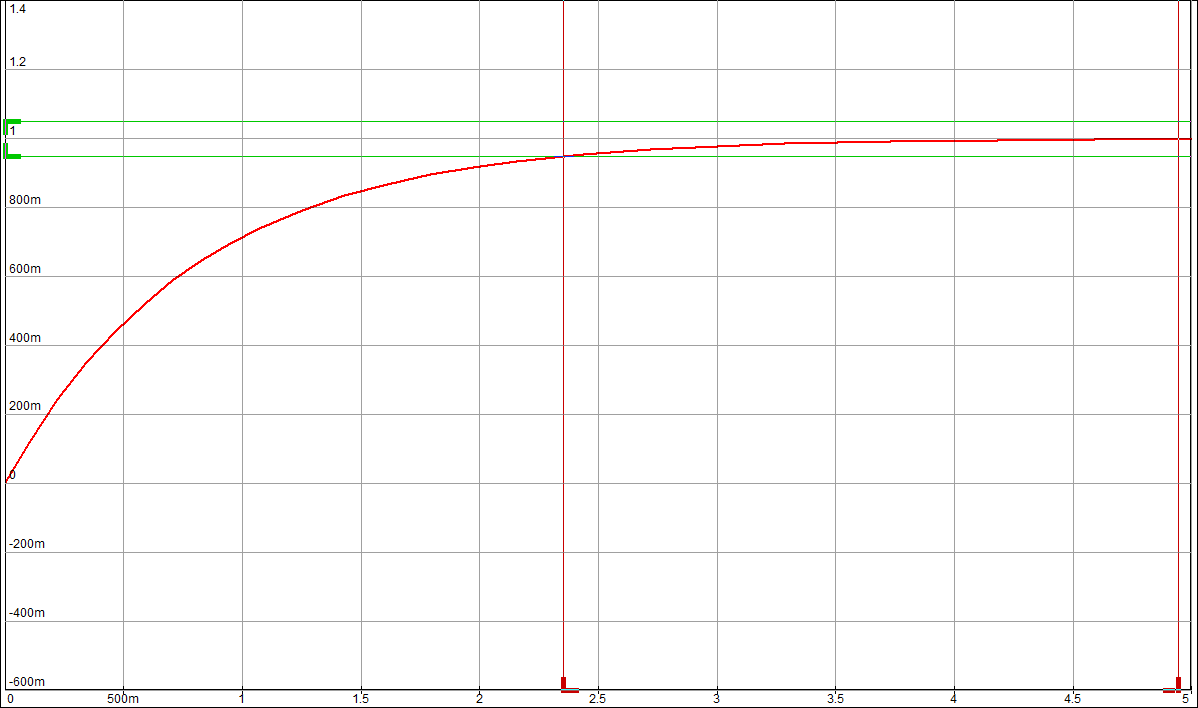 Рисунок 8 – Переходная характеристика инерционного звена (при Т=800 мс) 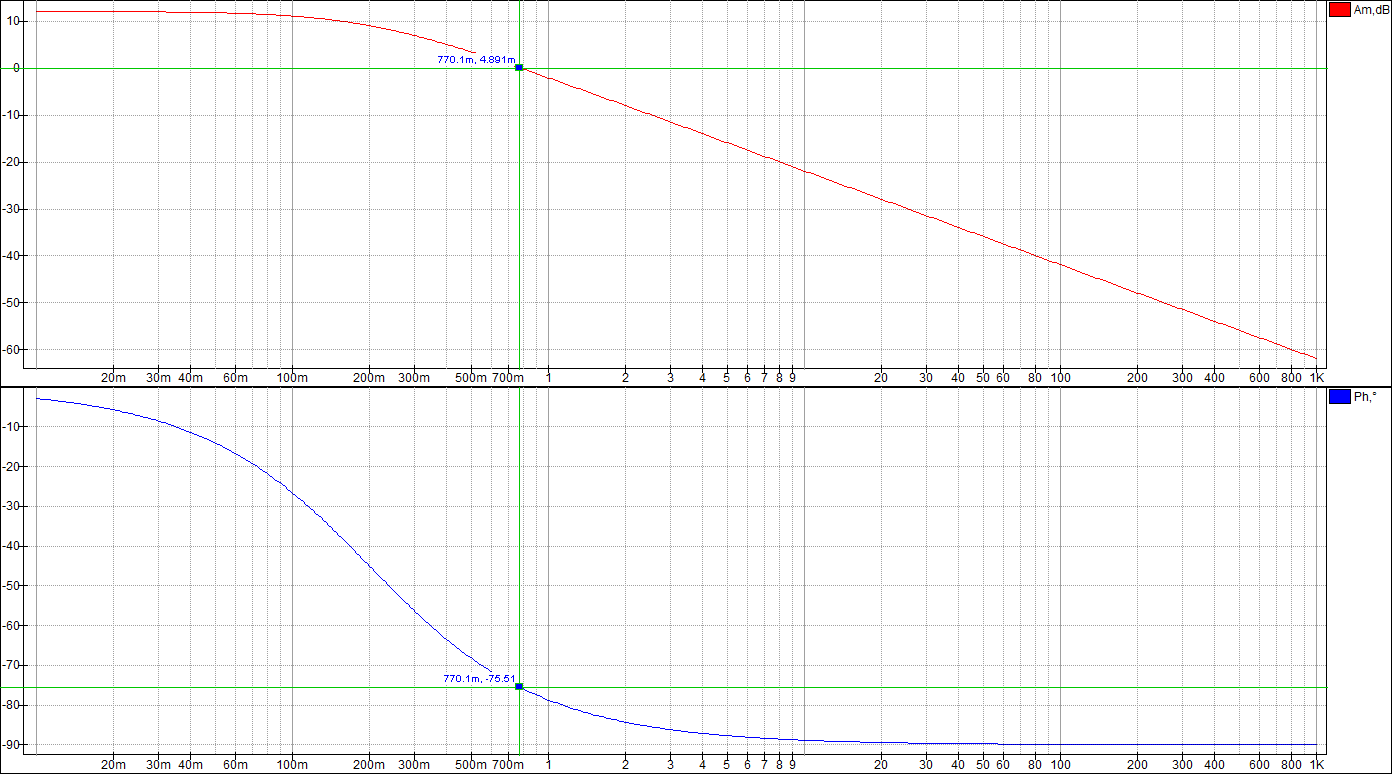 Рисунок 9 – ЛАЧХ и ЛФЧХ инерционного звена (при Т=800 мс) Таблица 1 – Таблица найденных значений ,  и 
По таблице значений построим графики зависимостей. 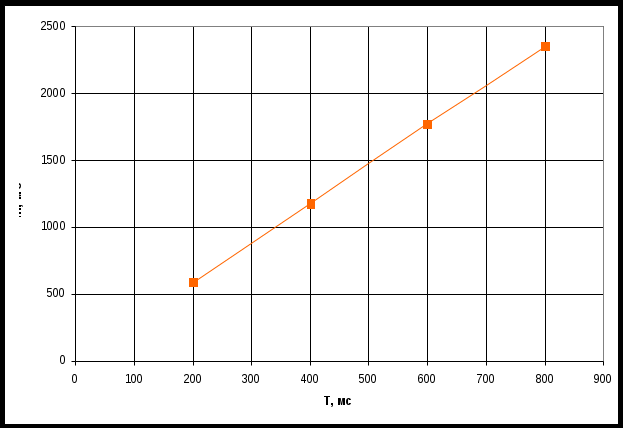 Рисунок 10 – График зависимости 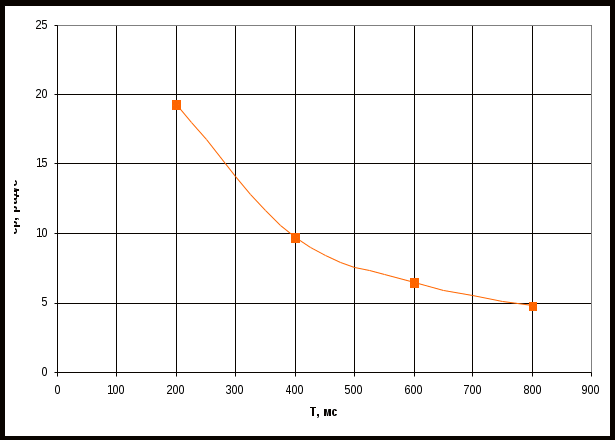 Рисунок 11 – График зависимости 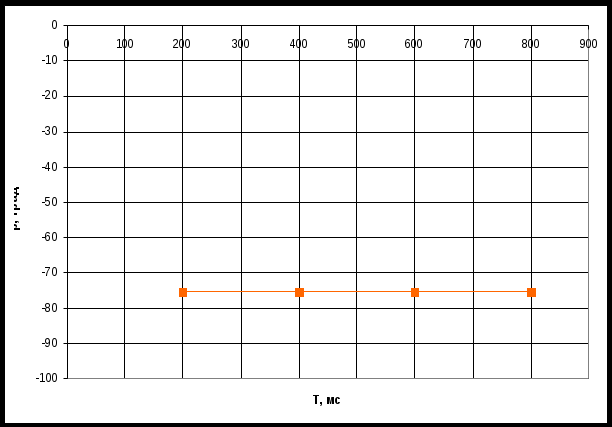 Рисунок 12 – График зависимости Вывыдо: при увеличении постоянной времени инерционного звена: - время переходного процесса линейно увеличивается; - частота среза уменьшается. Проверим это  ,откуда 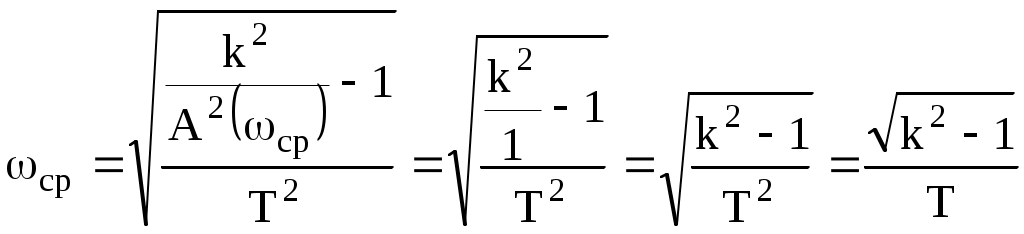 .Откуда при Т=200 мс  =19,36 рад/с, при Т=400 мс =9,68 рад/с, при Т=600 мс =6,45 рад/с, при Т=800 мс =4,8 рад/с. Как видно, экспериментальные данные верны – частота среза изменяется обратно пропорционально постоянной времени.- фаза – постоянна. 2 Исследование инерционного форсирующего звена 2.1 Собрать схему электронной модели инерционного форсирующего звена. Принять = =100 кОм,  =1 мкФ. Для заданного варианта выбрать значение постоянной времени T (200 мс), принять постоянную времени τ=0,1T и коэффициент передачи звена k=2. По формулам рассчитать параметры остальных элементов модели. Напряжение E источника питания электронной модели принять равным 0,5 В.2.2 Снять переходную характеристику и определить величину скачка  переходной характеристики при t=0 , установившееся значение  и время переходного процесса . Рассчитать параметр  .2.3 Получить экспериментальные ЛАЧХ и ЛФЧХ, замерить частоту среза и значение фазы  на этой частоте.2.4 Установить соотношения значений постоянных времени τ = 0,2T , τ = 0,3T , τ = 0,4T и повторить выполнение заданий пп. 2.2 и 2.3, пересчитав параметры модели в соответствии с п. 2.1. 2.5 Построить графики зависимостей λ=f(τ),  ,  и  и сравнить их с аналогичными зависимостями, полученными в п. 1.5.2.6 Оценить влияние постоянной времени форсирующего звена на характеристики инерционного форсирующего звена. 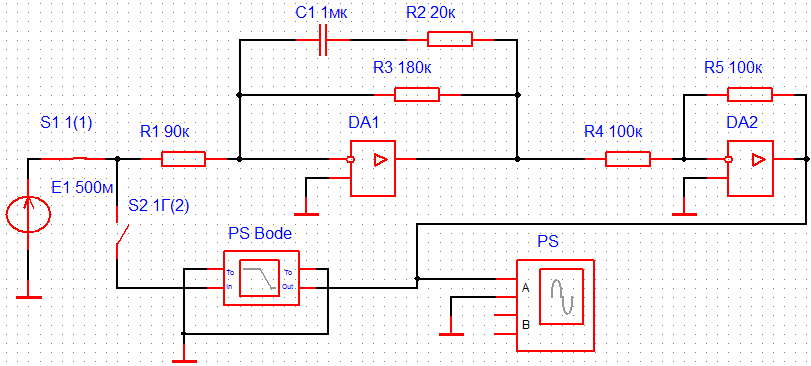 Рисунок 13 – Схема для исследования форсирующего инерционного звена 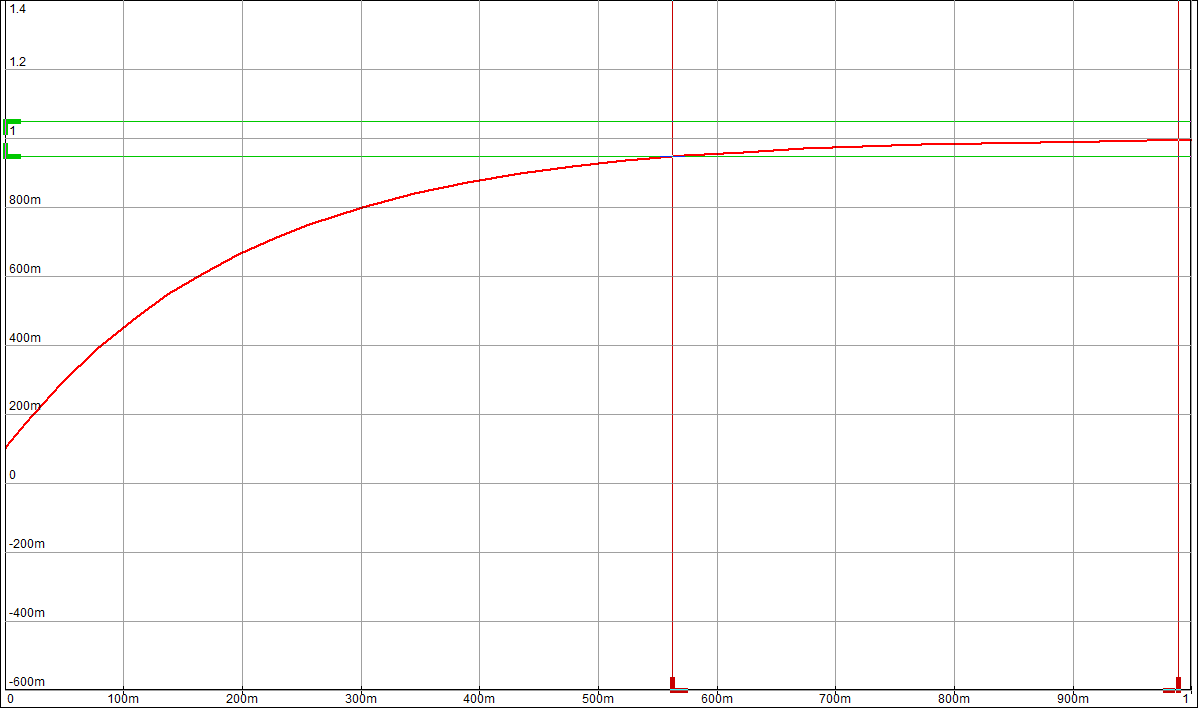 Рисунок 14 – Переходная характеристика форсирующего инерционного звена (при τ=0,1T) 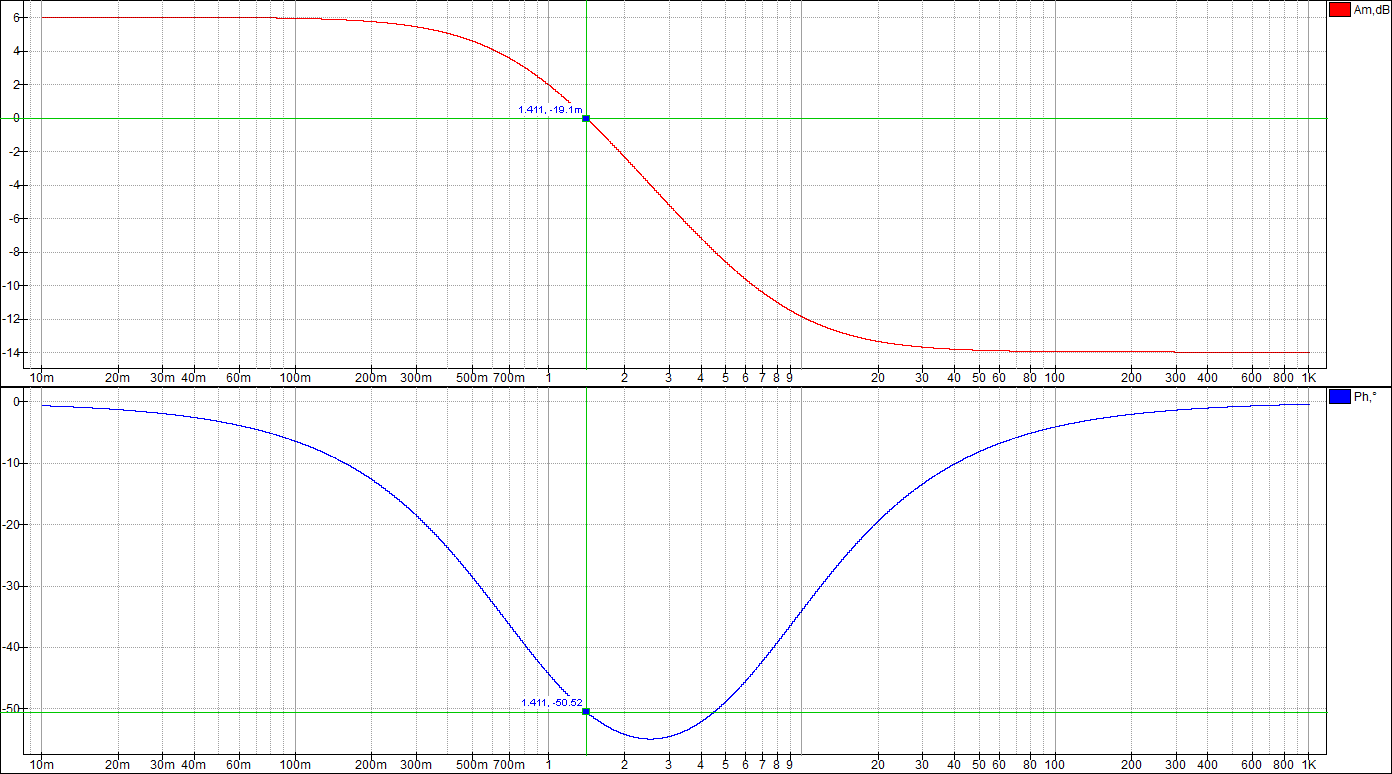 Рисунок 15 – ЛАЧХ и ЛФЧХ форсирующего инерционного звена (при τ=0,1T) 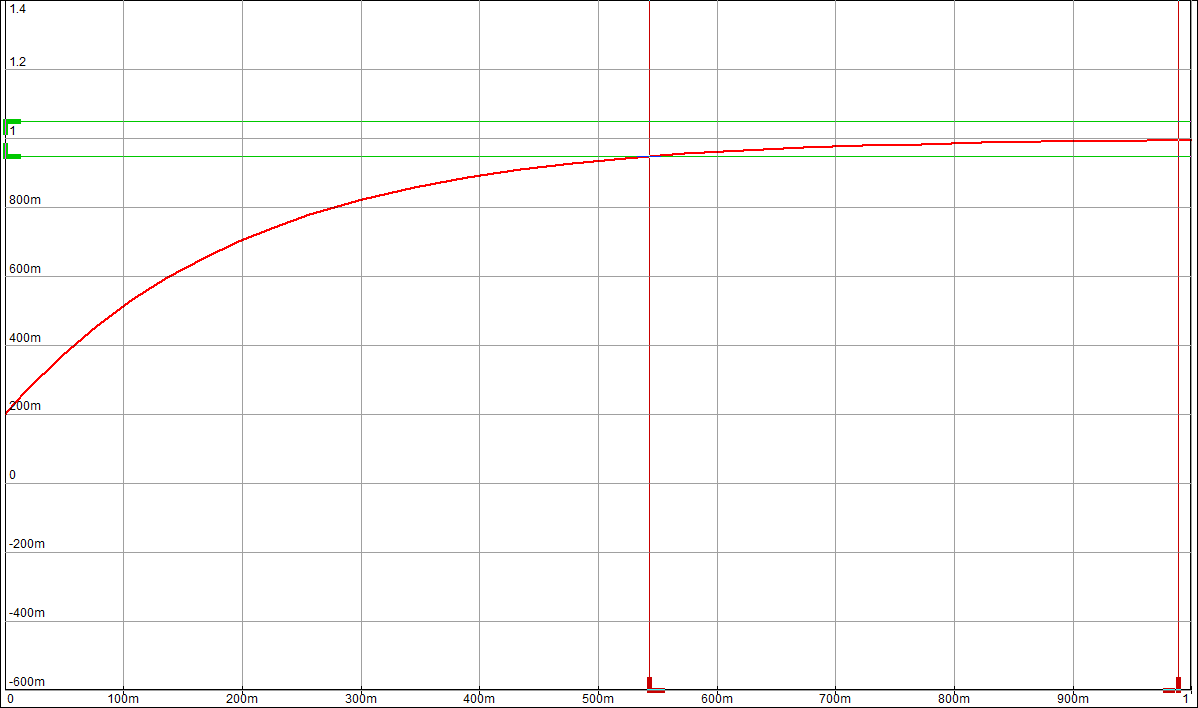 Рисунок 16 – Переходная характеристика форсирующего инерционного звена (при τ=0,2T) 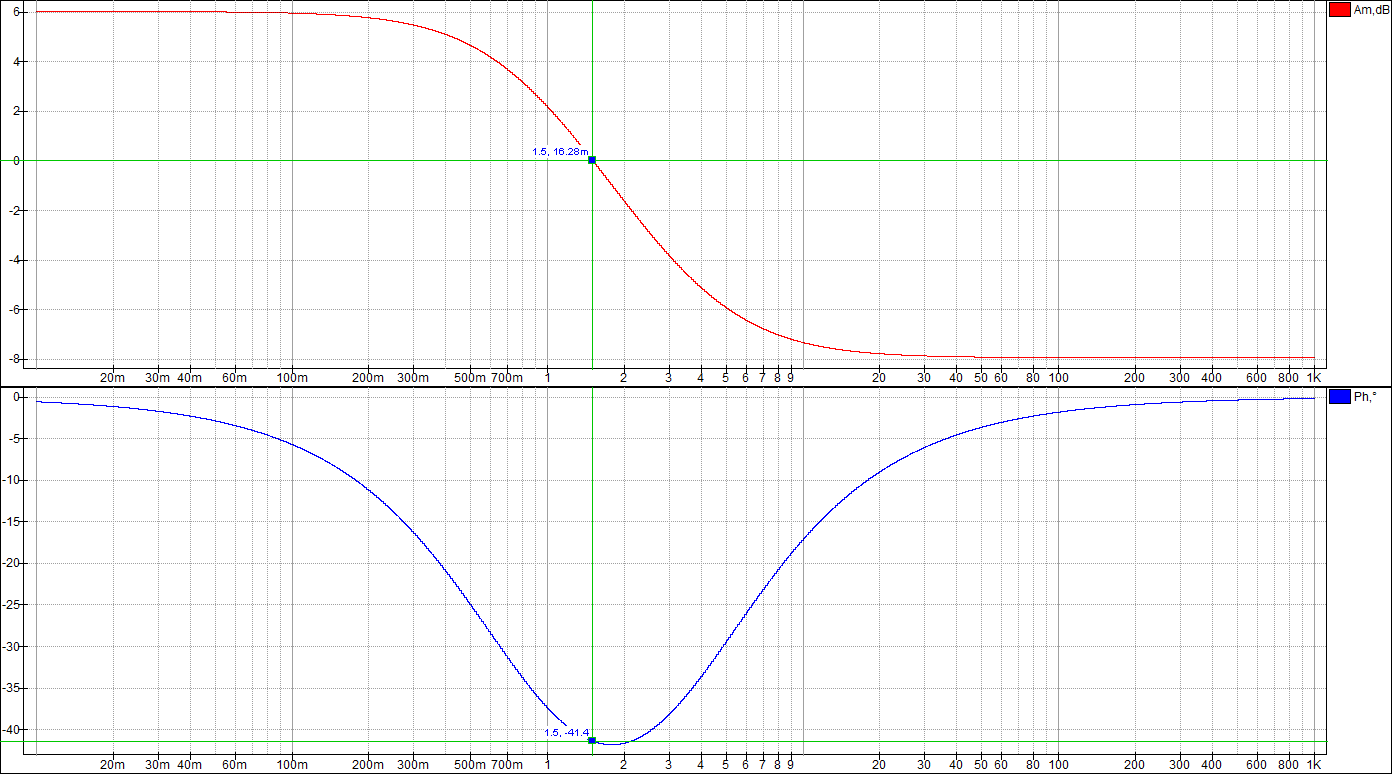 Рисунок 17 – ЛАЧХ и ЛФЧХ форсирующего инерционного звена (при τ=0,2T) 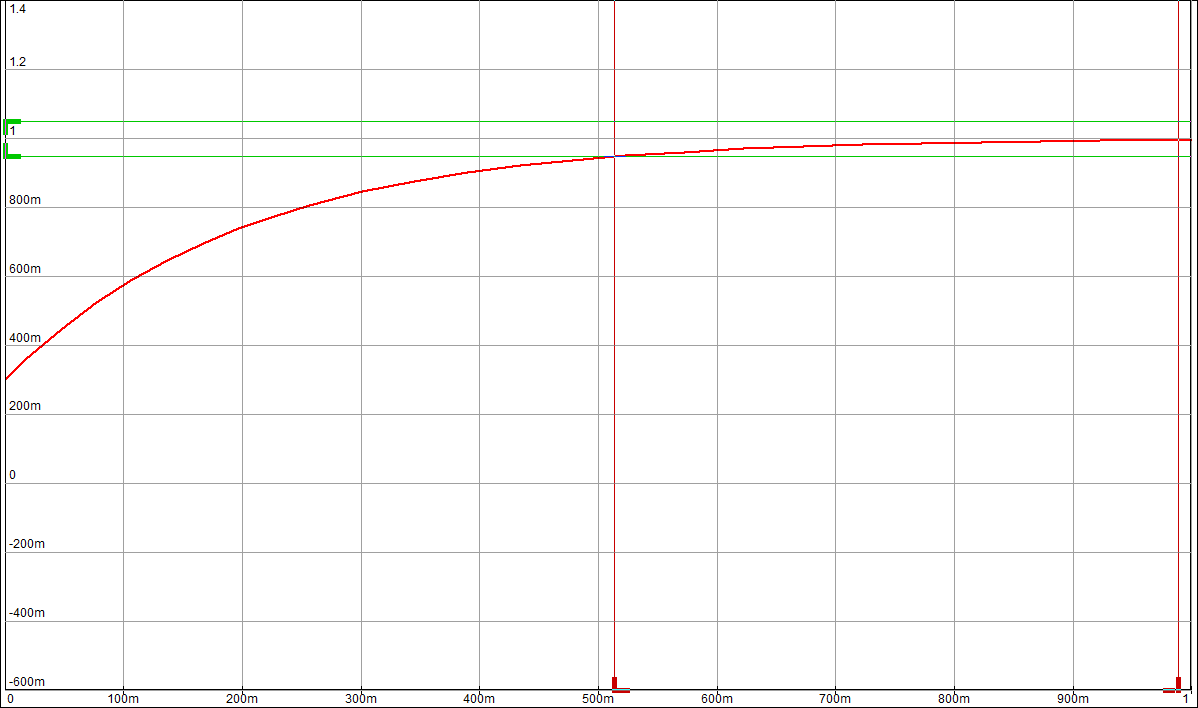 Рисунок 18 – Переходная характеристика форсирующего инерционного звена (при τ=0,3T) 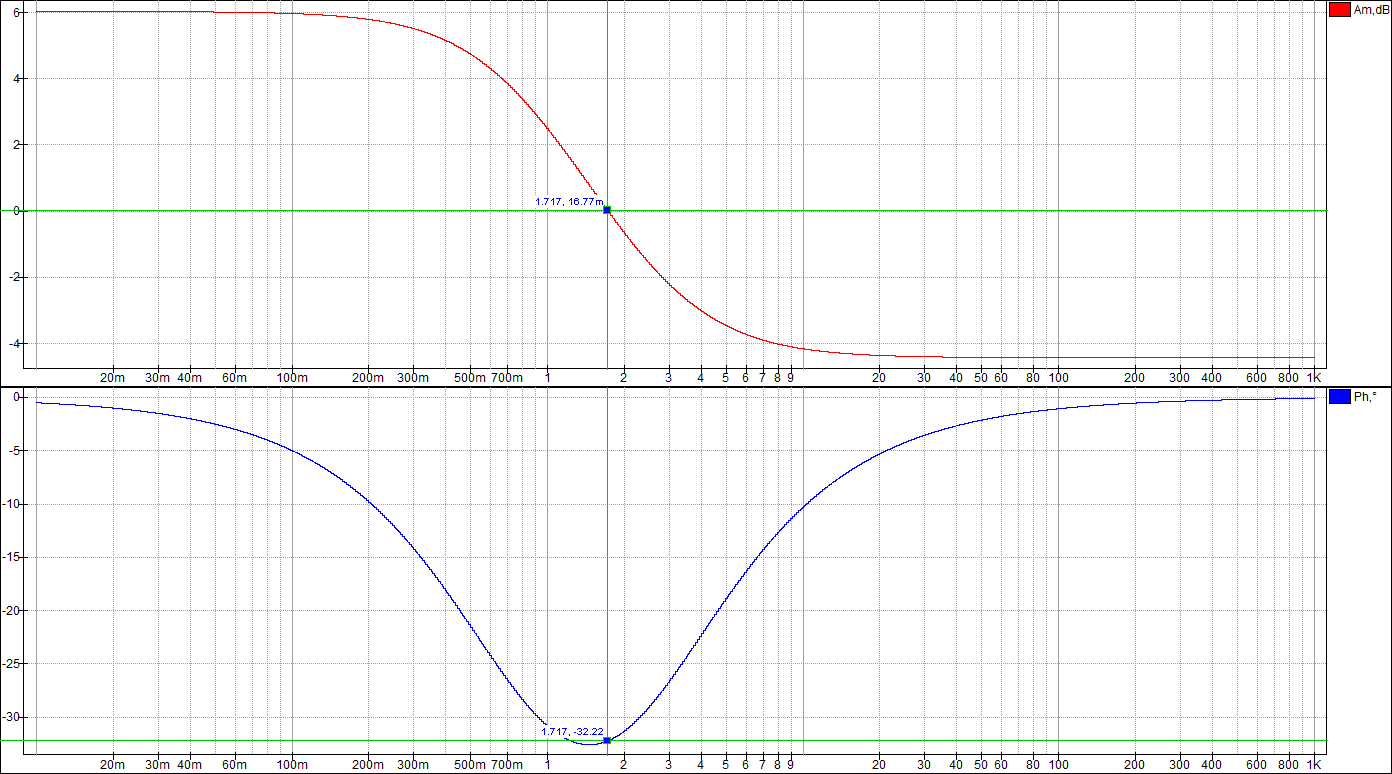 Рисунок 19 – ЛАЧХ и ЛФЧХ форсирующего инерционного звена (при τ=0,3T) 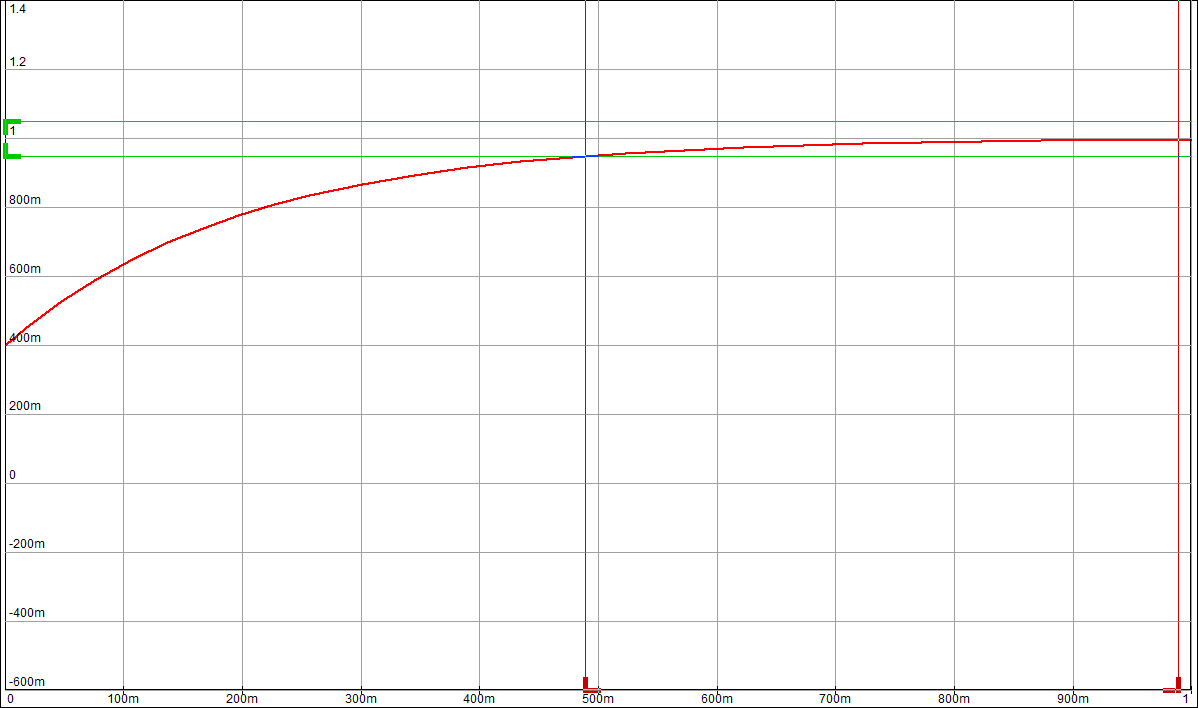 Рисунок 20 – Переходная характеристика форсирующего инерционного звена (при τ=0,4T) 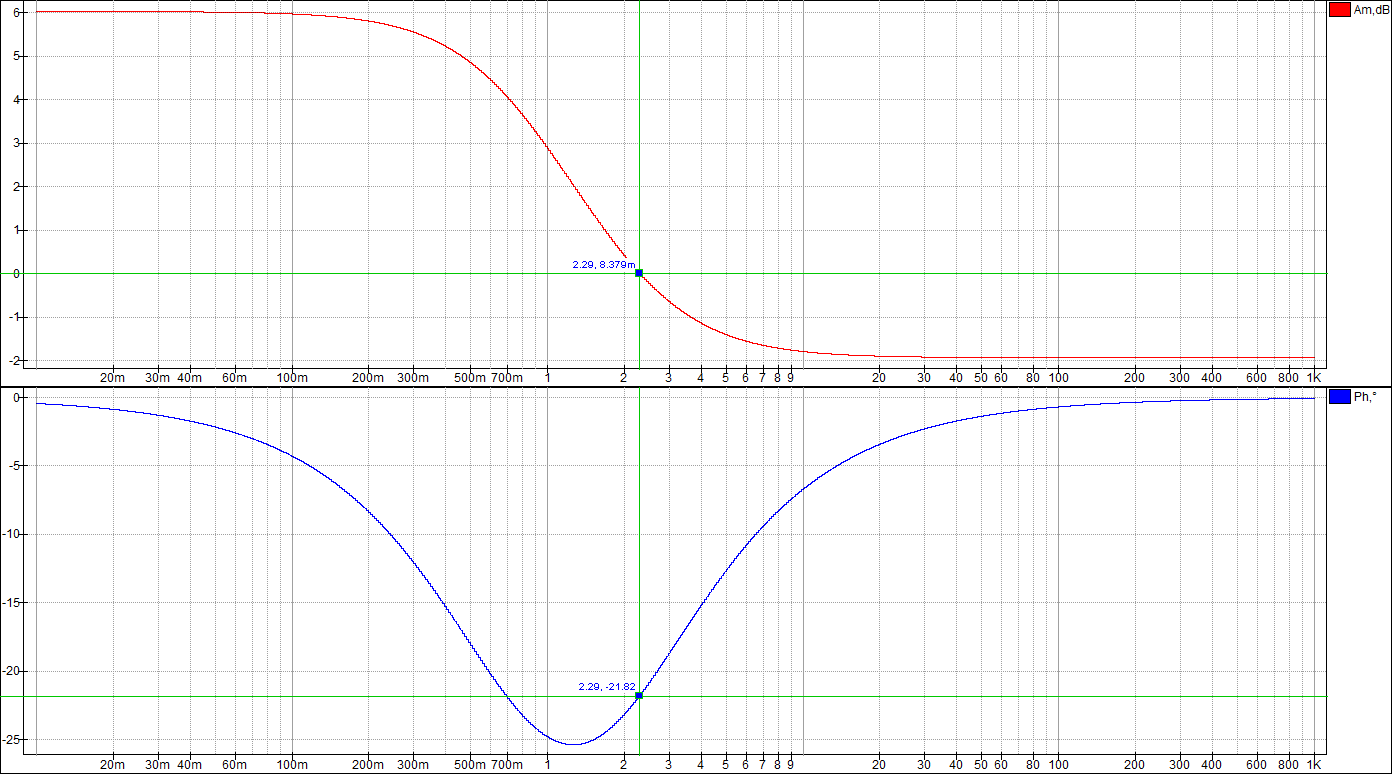 Рисунок 21 – ЛАЧХ и ЛФЧХ форсирующего инерционного звена (при τ=0,4T) Таблица 2 – Таблица найденных значений  , , и
По таблице значений построим графики зависимостей. 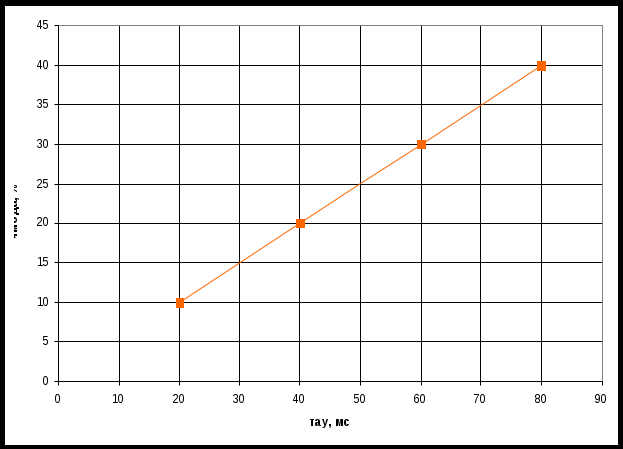 Рисунок 22 – График зависимости λ=f(τ) 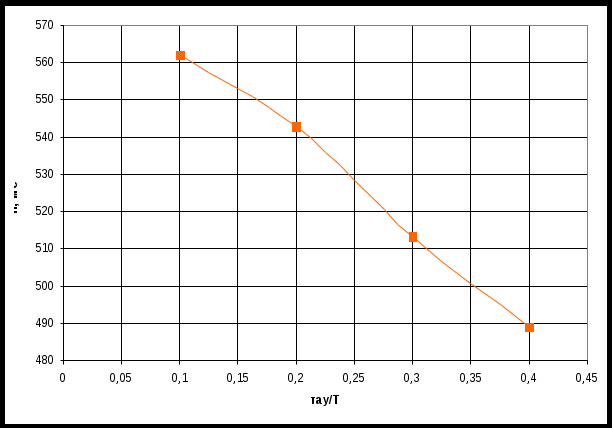 Рисунок 23 – График зависимости 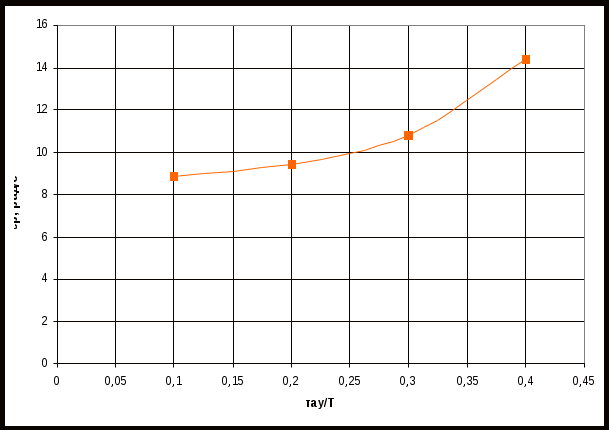 Рисунок 24 – График зависимости 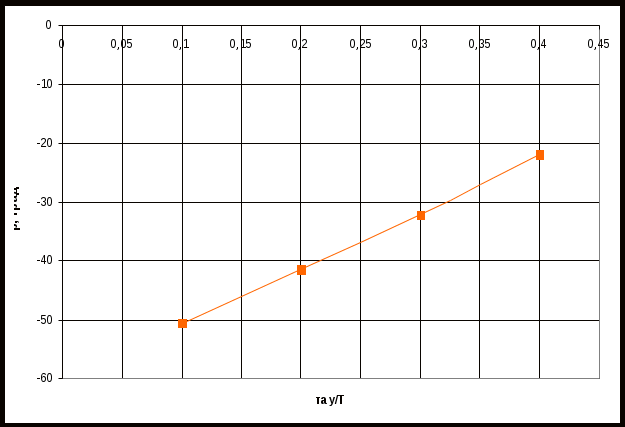 Рисунок 25 – График зависимости Выводы: при увеличении постоянной времени форсирующего инерционного звена (а, следовательно, при увеличении отношения  ):- возрастает, а именно  , т.е. зависимость линейная;- время переходного процесса уменьшается, тогда, как у инерционного звена время переходного процесса увеличивалось; - частота среза увеличивается, тогда, как у инерционного звена частота среза уменьшалась; - фаза возрастает, тогда, как у инерционного звена фаза была постоянной. 3.1 Собрать схему модели звена второго порядка в соответствии с рис. 5.11. Приняв  = = =100 кОм, = =1 мкФ, ξ=0,7 и выбрав значения постоянной времени T (200 мс) и коэффициента передачи k (4) согласно индивидуальному варианту, рассчитать значения остальных параметров модели по формулам: ,  ,  .3.2 Установить напряжение питания модели, равное  , снять переходную характеристику и определить время переходного процесса , фиксируя при этом осциллографом максимальное  значение выходного напряжения.3.3 Рассчитать перерегулирование  ,где  =1 В. При правильном расчете параметров электронной модели колебательного звена перерегулирование не должно превышать 5 %.3.4 Получить экспериментальные ЛАЧХ и ЛФЧХ, замерить частоту среза , значение фазы на частоте среза и определить запас устойчивости по фазе  .3.5 Установить значения ξ=0,5, ξ=0,3, ξ=0,1, а также ξ=1, ξ=2, ξ=3 и повторить выполнение пп. 3.2 – 3.4. 3.6 Построить графики зависимостей  ,  ,  ,  и  . 3.7 Оценить влияние коэффициента демпфирования на характеристики звеньев второго порядка. 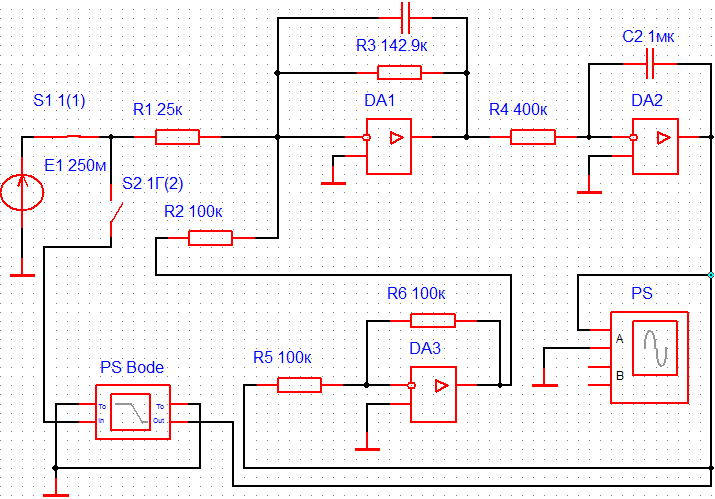 Рисунок 26 – Схема для исследования звена второго порядка 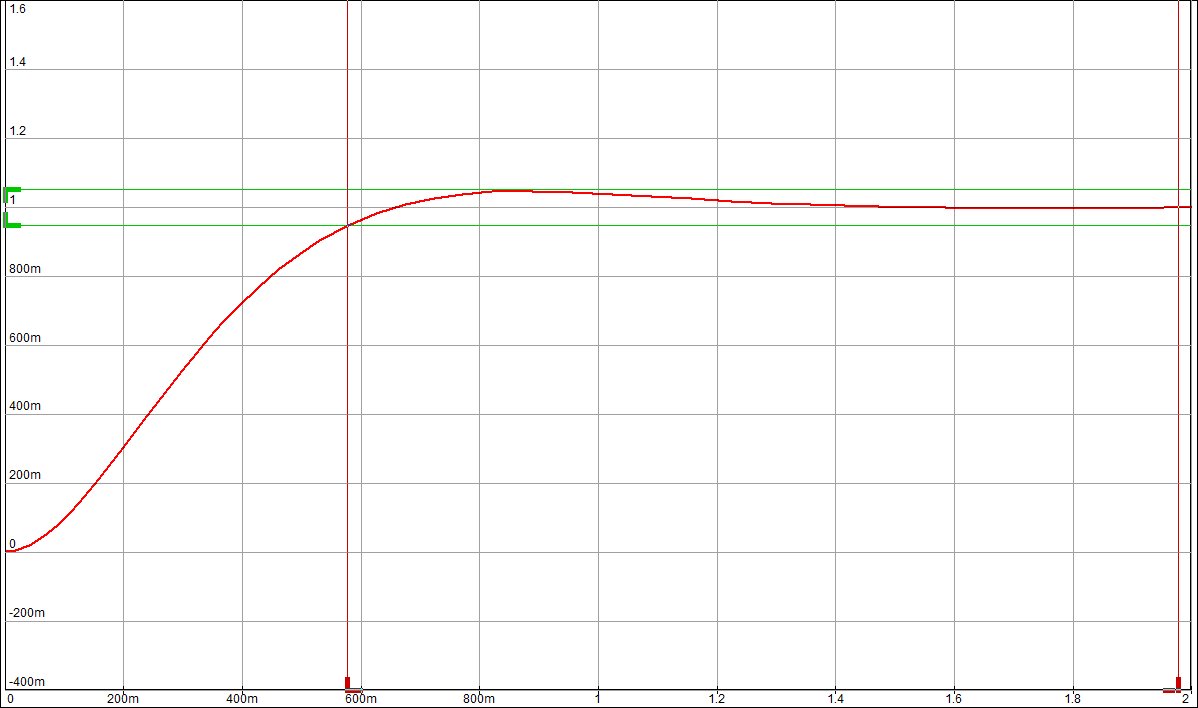 Рисунок 27 – Переходная характеристика звена второго порядка (при 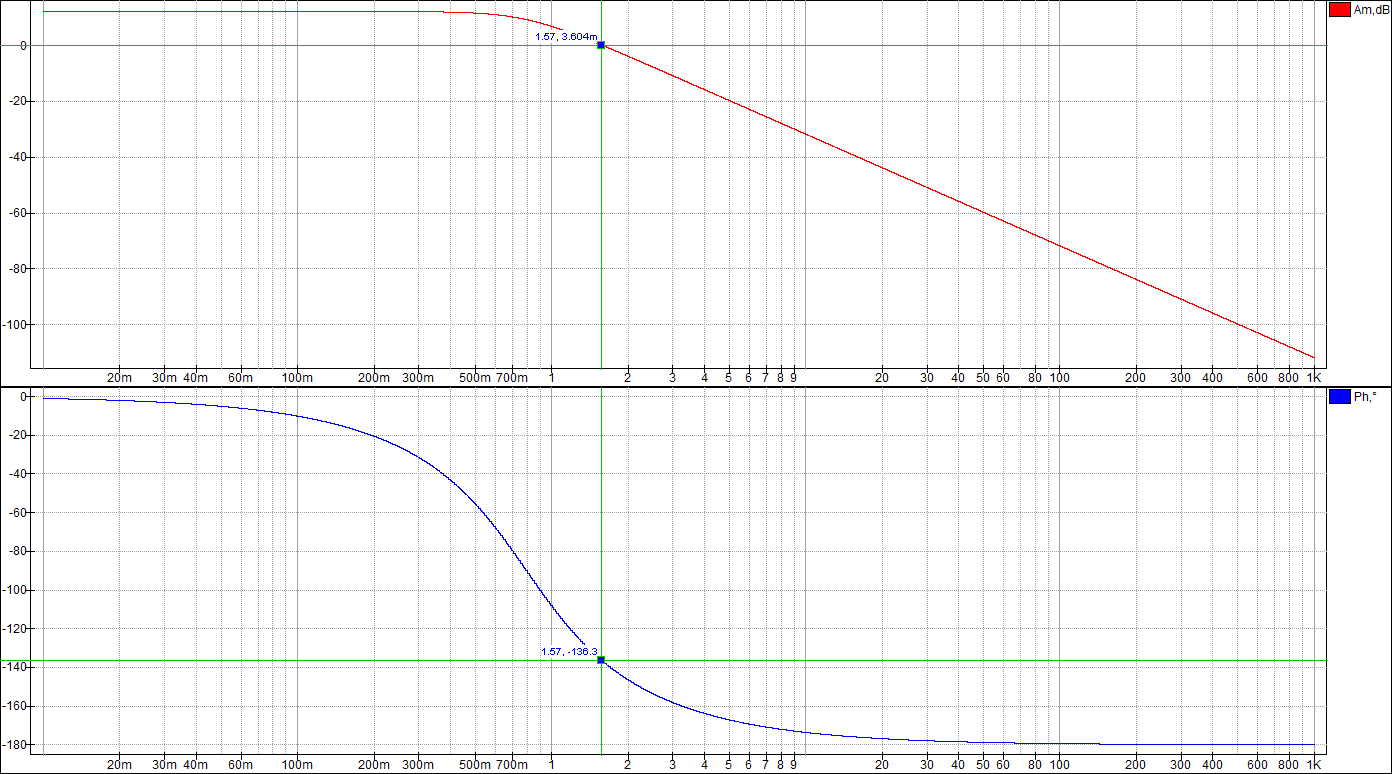 ) Рисунок 28 – ЛАЧХ и ЛФЧХ звена второго порядка (при 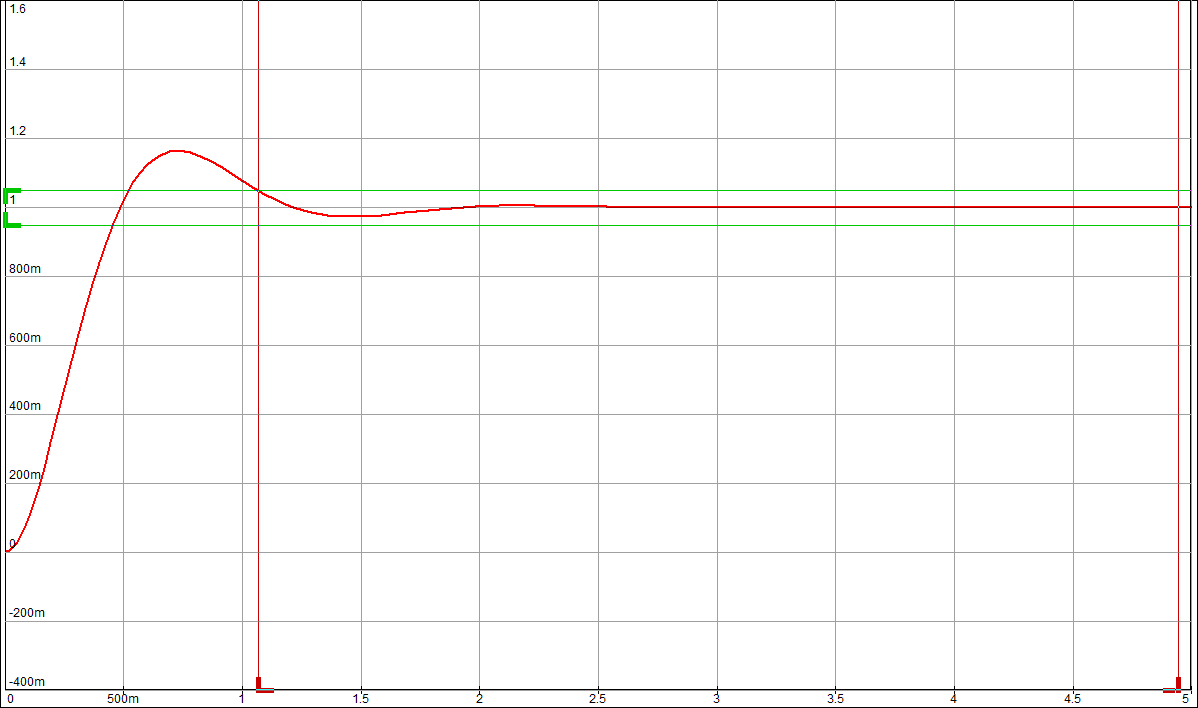) Рисунок 29 – Переходная характеристика звена второго порядка (при 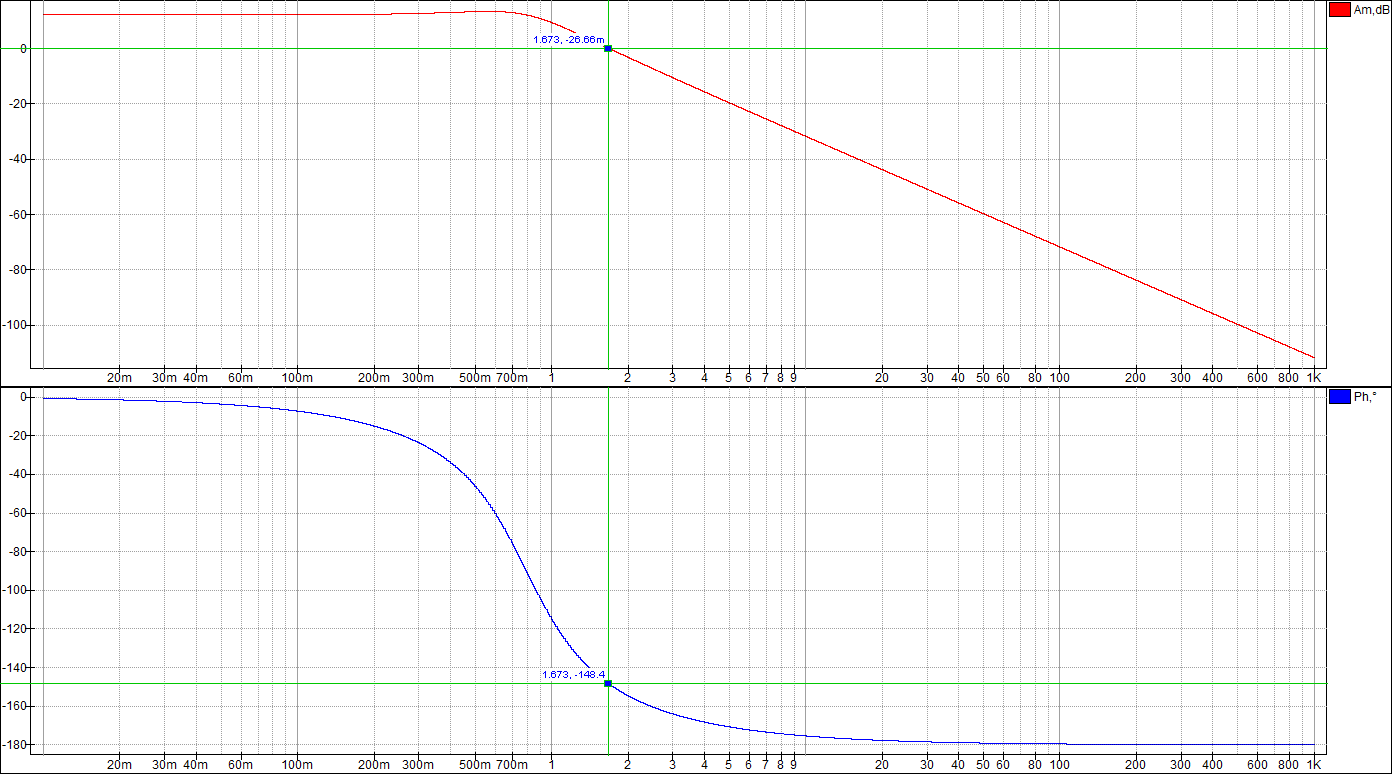 ) Рисунок 30 – ЛАЧХ и ЛФЧХ звена второго порядка (при 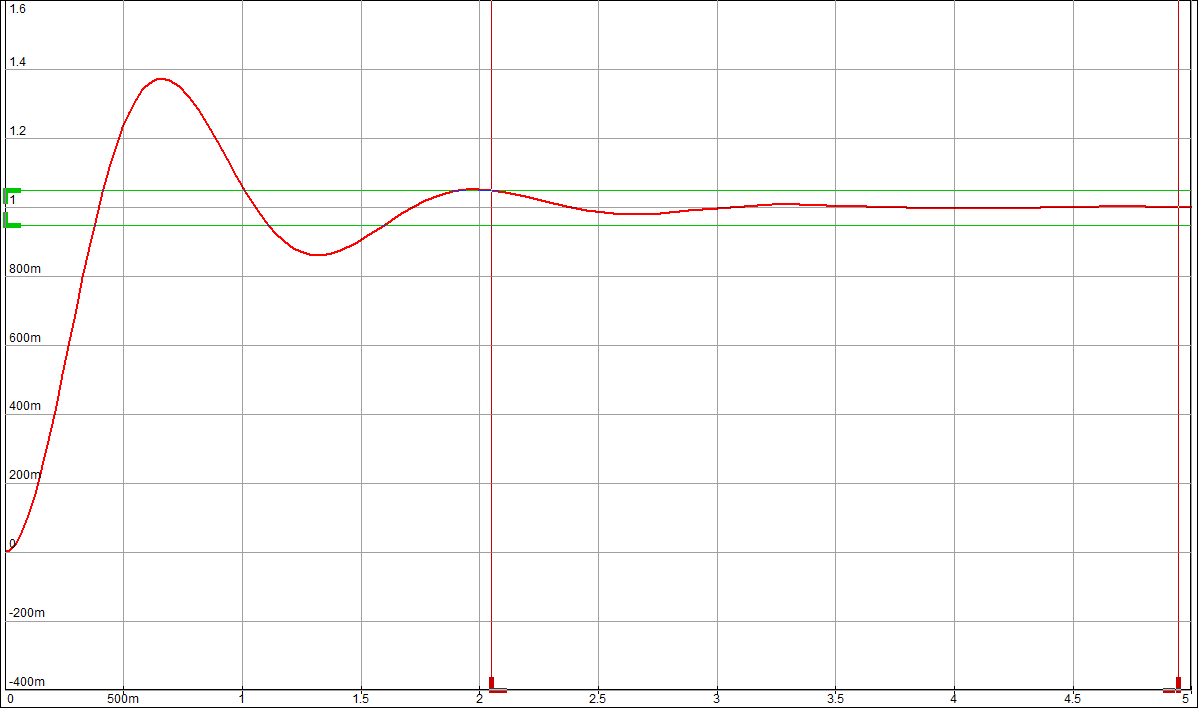) Рисунок 31 – Переходная характеристика звена второго порядка (при 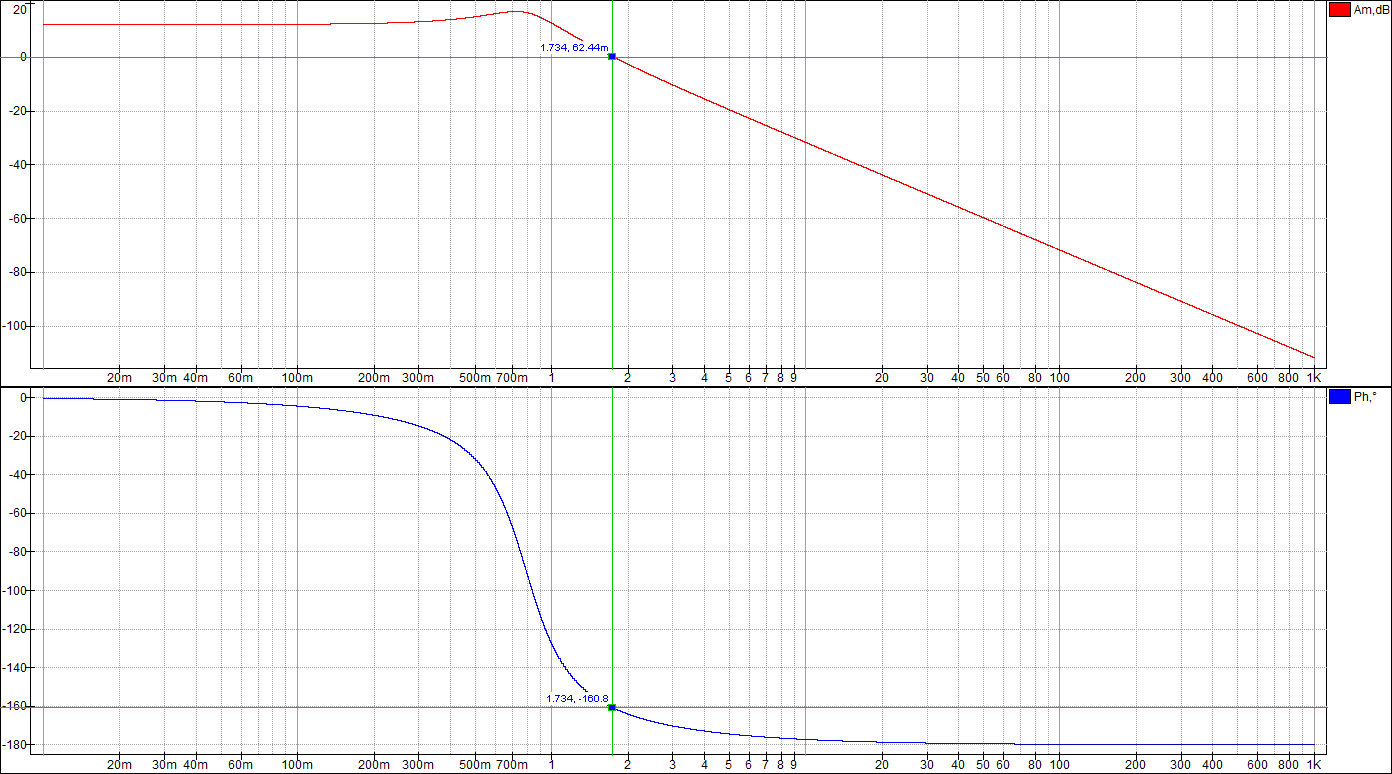 ) Рисунок 32 – ЛАЧХ и ЛФЧХ звена второго порядка (при 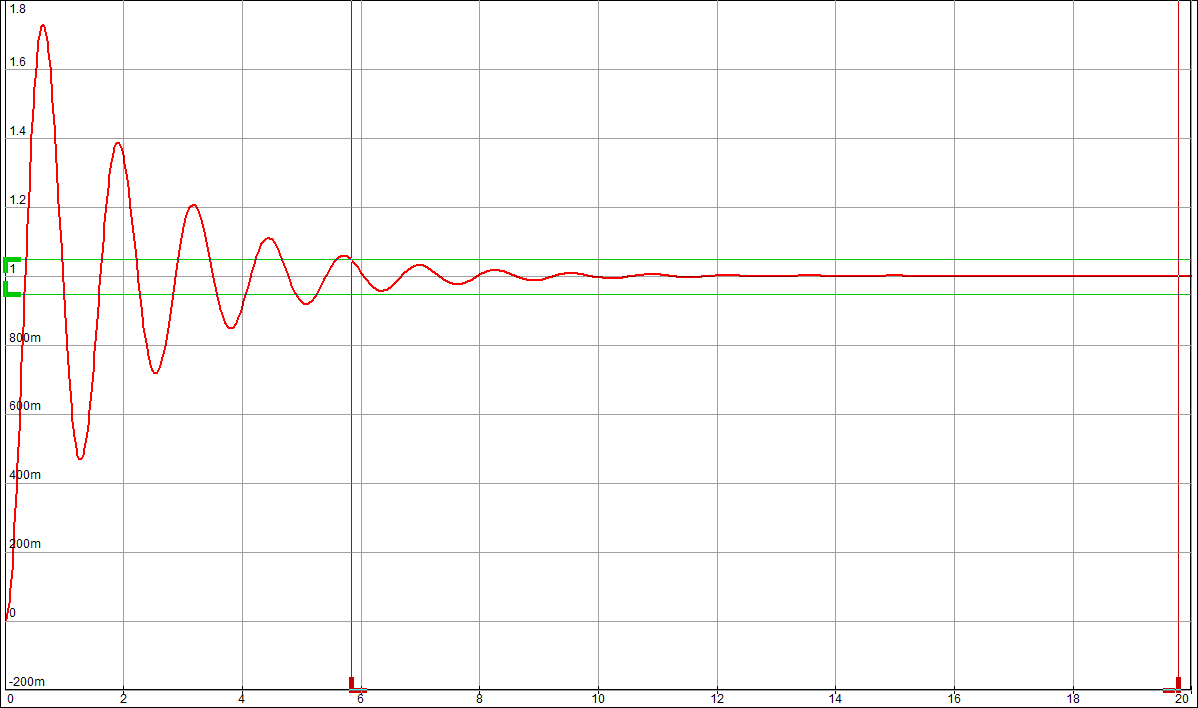) Рисунок 33 – Переходная характеристика звена второго порядка (при 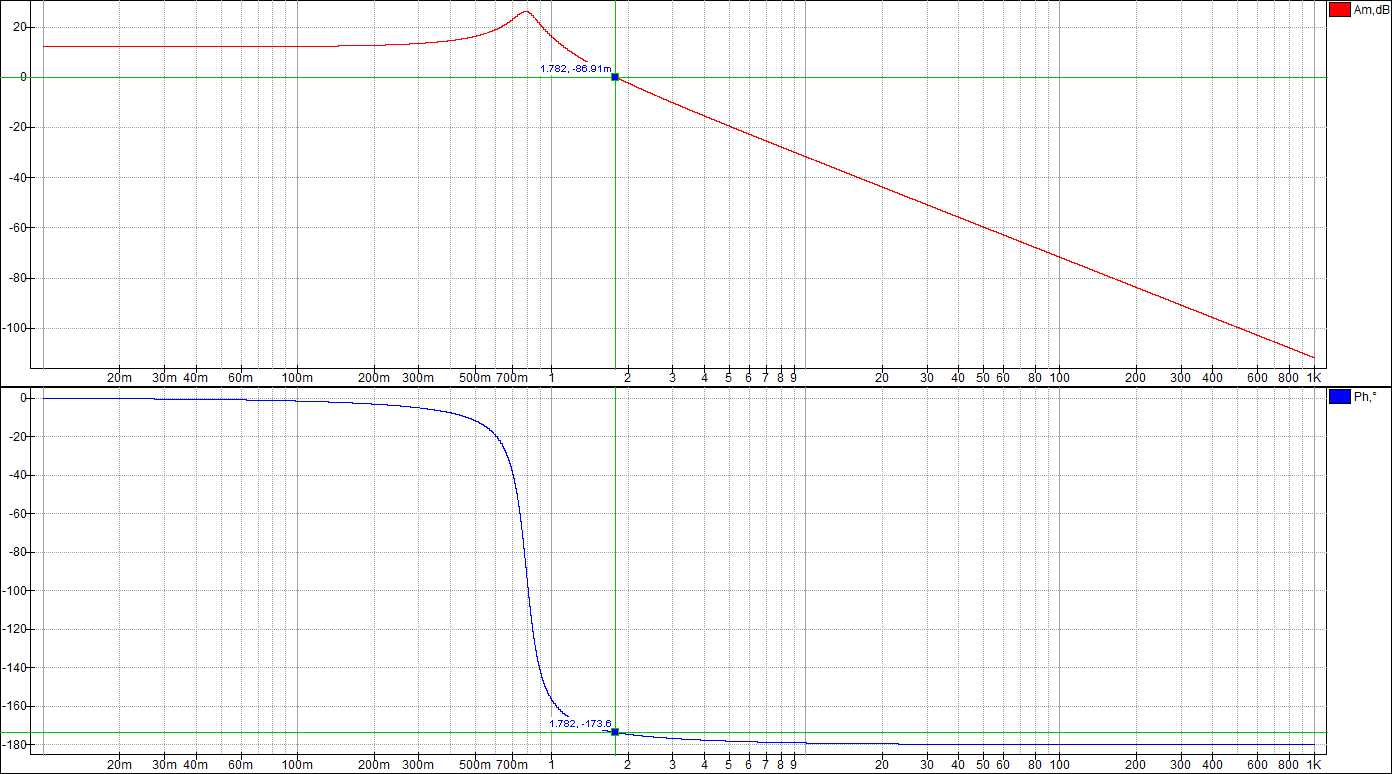 ) Рисунок 34 – ЛАЧХ и ЛФЧХ звена второго порядка (при 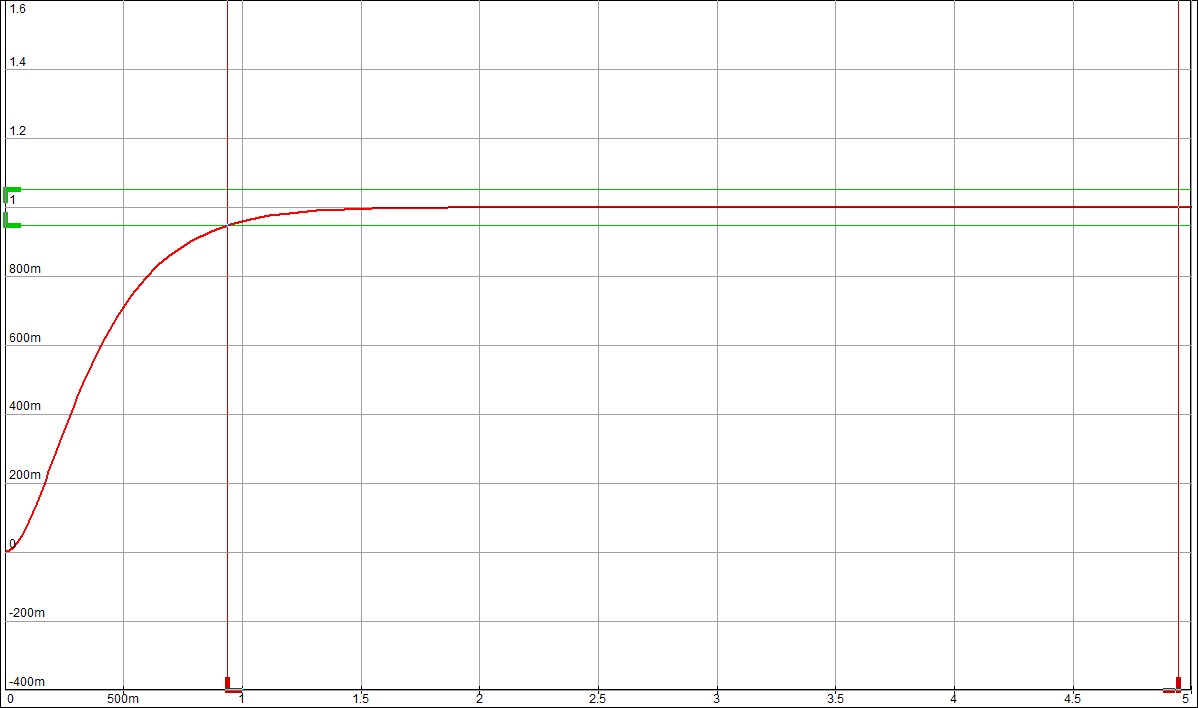) Рисунок 35 – Переходная характеристика звена второго порядка (при 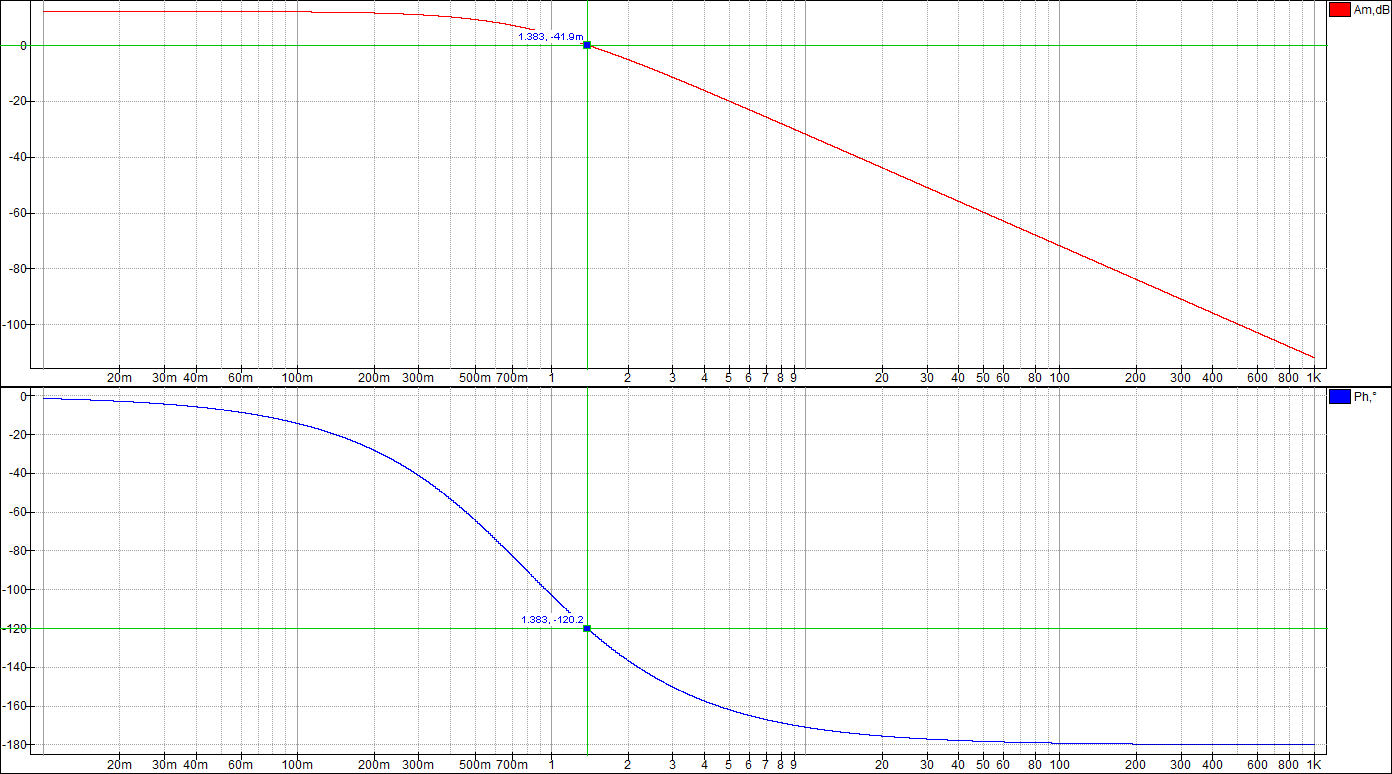 ) Рисунок 36 – ЛАЧХ и ЛФЧХ звена второго порядка (при 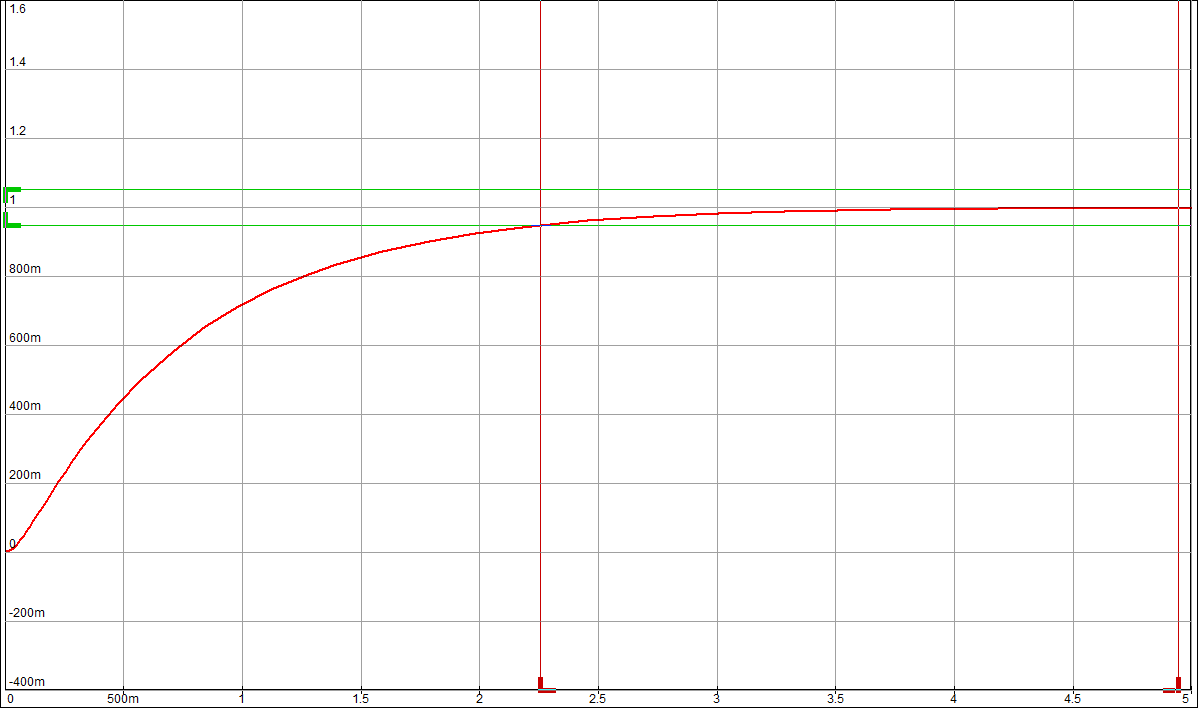) Рисунок 37 – Переходная характеристика звена второго порядка (при 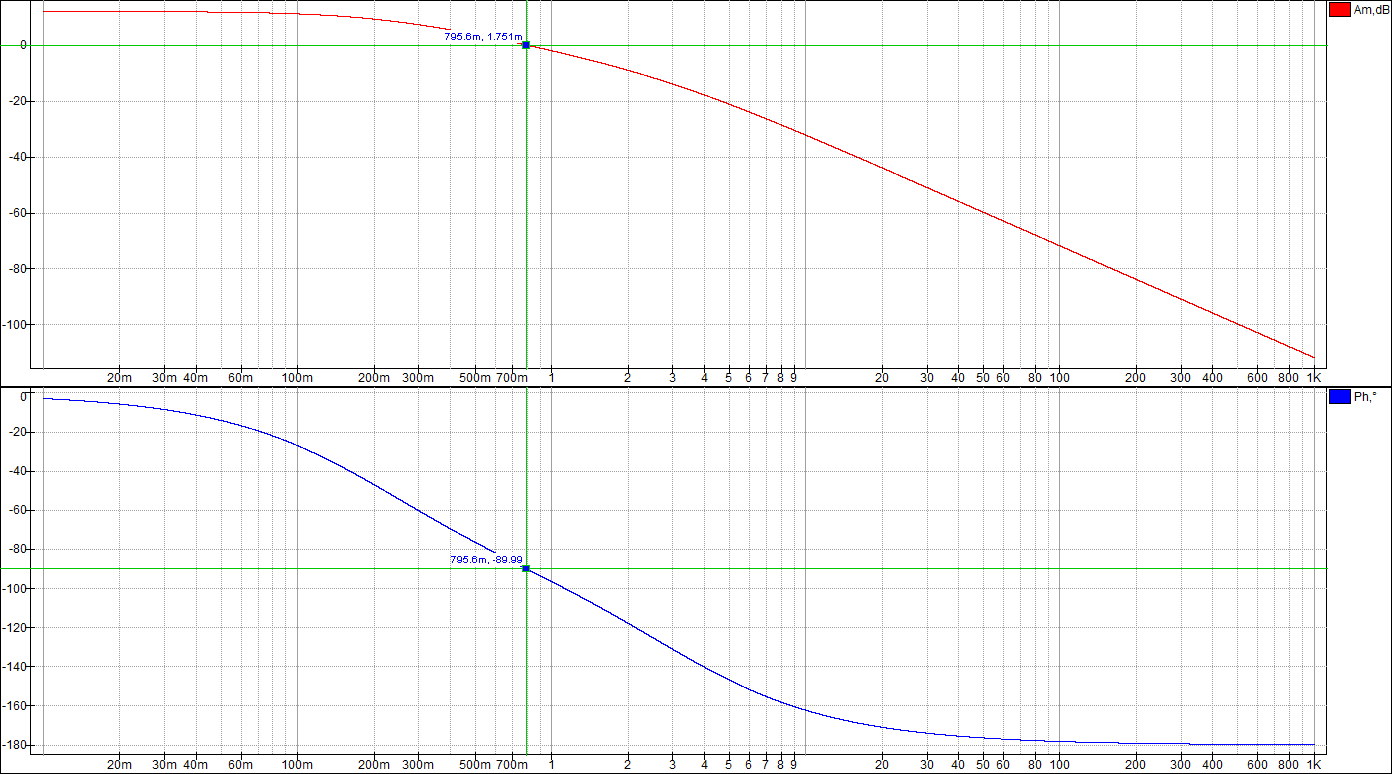 ) Рисунок 38 – ЛАЧХ и ЛФЧХ звена второго порядка (при 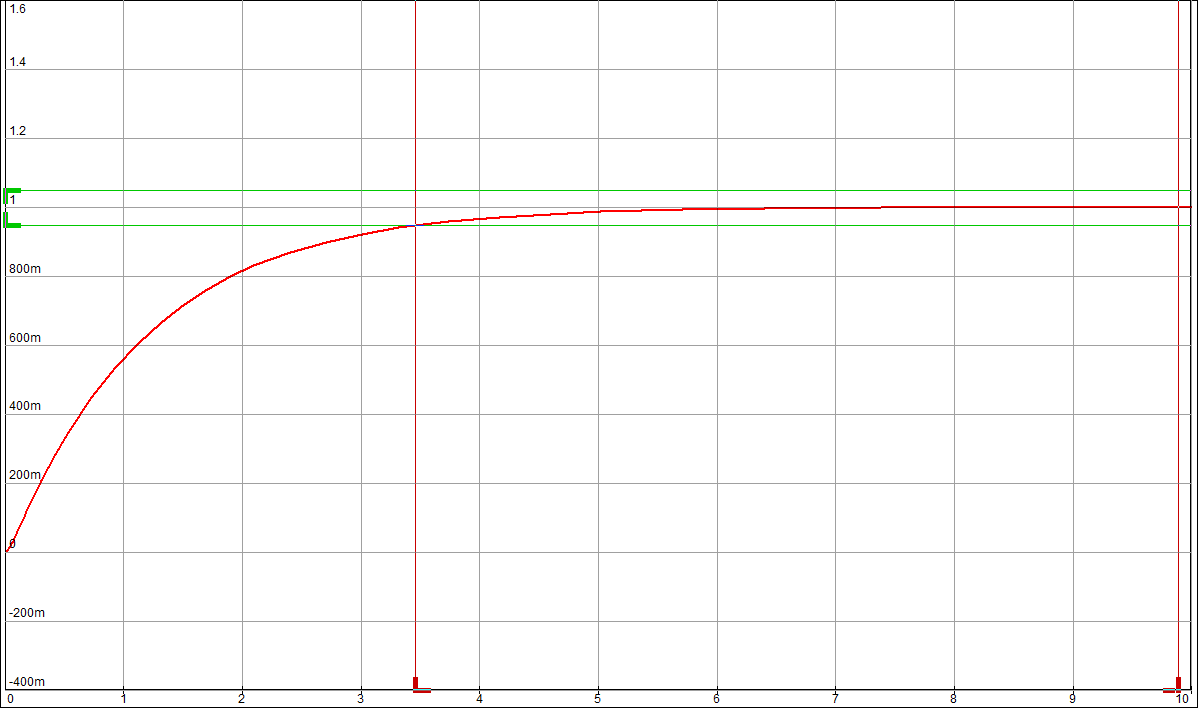) Рисунок 39 – Переходная характеристика звена второго порядка (при 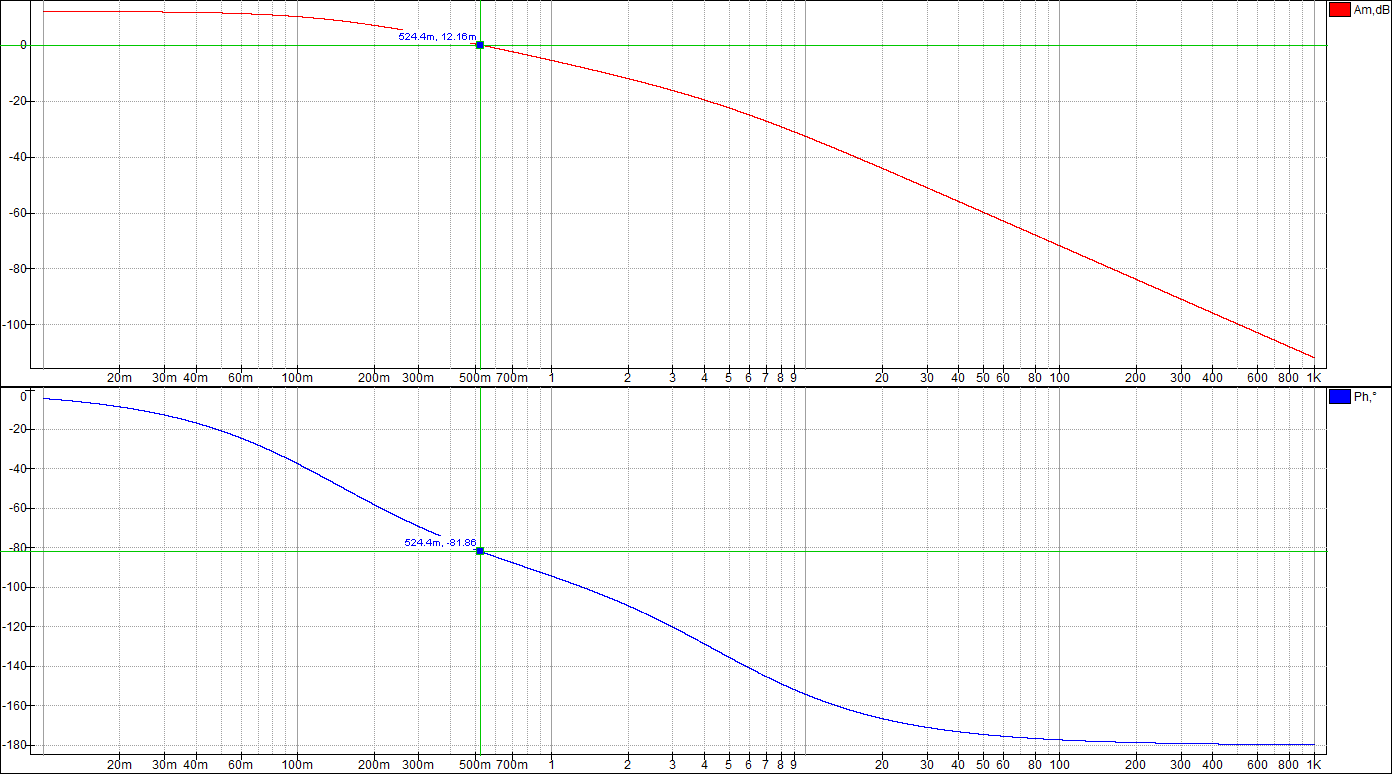 ) Рисунок 40 – ЛАЧХ и ЛФЧХ звена второго порядка (при )Таблица 3 – Таблица найденных значений , , и
По таблице значений построим графики зависимостей. 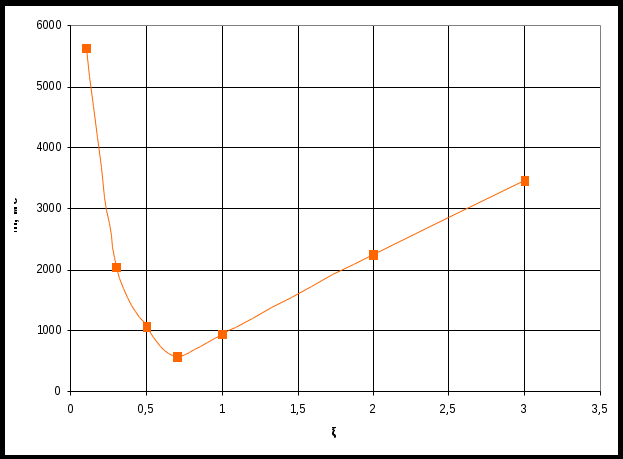 Рисунок 41 – График зависимости 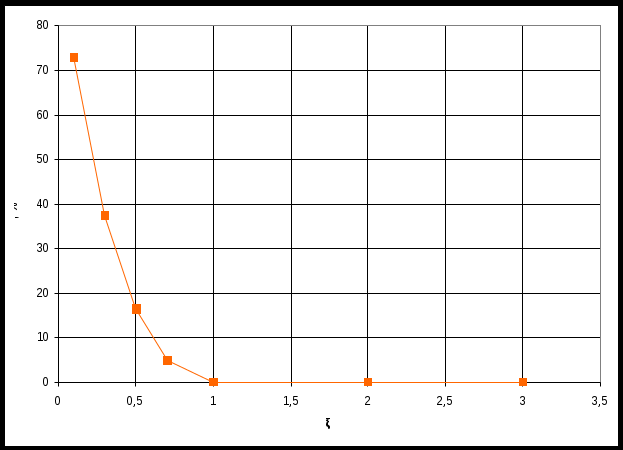 Рисунок 42 – График зависимости 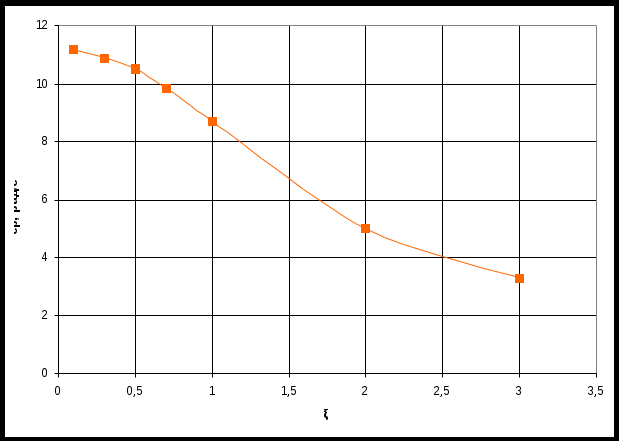 Рисунок 43 – График зависимости 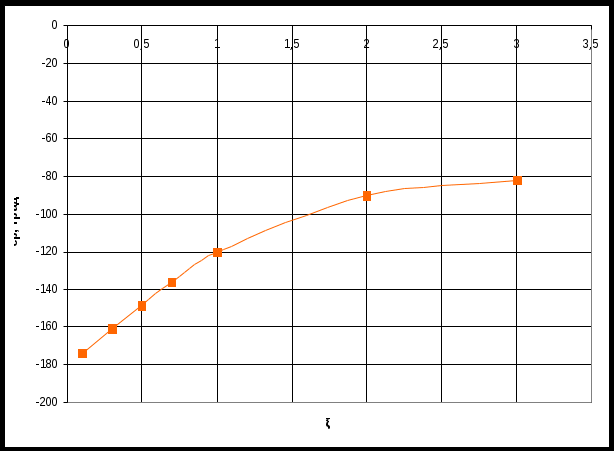 Рисунок 44 – График зависимости 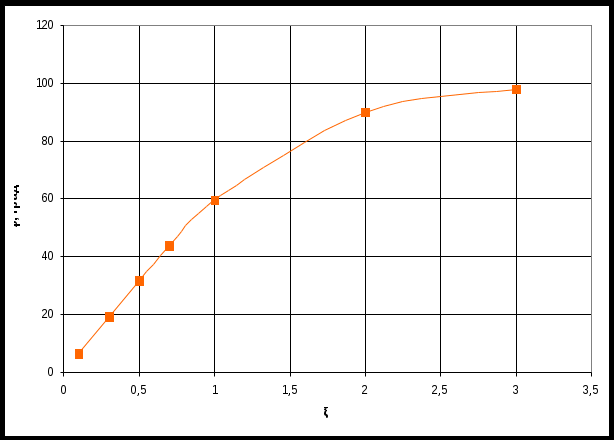 Рисунок 45 – График зависимости Выводы при увеличении значения  звена второго порядка:- время переходного процесса уменьшается при увеличении от 0 до 0,7 и возрастает при значении >0,7, следовательно, зависимость нелинейная. Время переходного процесса имеет минимальное значение, когда =0,7;- перерегулирование уменьшается, а при  равно 0;- частота среза уменьшается; - фаза и запас устойчивости по фазе возрастают. 1. Как количественно величина постоянной времени связана с временем переходного процесса в инерционном звене? Время переходного процесса можно описать неравенством: ,где  – это расстояние от мнимой оси, являющейся границей устойчивости, до ближайшего корня (геометрически), т.е.  .В инерционном звене корень равен  , тогда, подставляя в выше приведенные выражения:  ,откуда  .Откуда, время переходного процесса меньше или равно трём постоянным времени. 2. Как изменятся характеристики инерционного форсирующего звена при τ>T и его реализация на электронной модели? При τ>T реализация на электронной модели инерционного форсирующего звена будет иметь вид (рисунок 46) 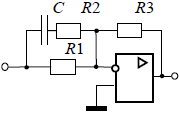 Рисунок 46 – Электронная модель инерционного форсирующего звена при τ>T Переходная характеристика будет иметь вид (рисунок 47). При t=0 переходная характеристика будет иметь начальный скачок, равный 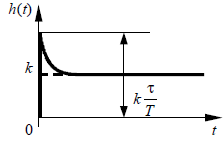 , то есть при τ>T начальный скачок будет выше установившегося значения. При t=∞ установившееся значение h(∞)=k . Рисунок 47 – Переходная характеристика инерционного форсирующего звена при τ>T ЛАЧХ и ЛФЧХ будут иметь вид (рисунок 48). При τ > T наклон ЛАЧХ +20 дБ/дек после частоты сопряжения 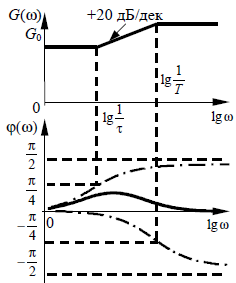 и нулевой наклон после  . ЛФЧХ в результате суммирования составляющих  и  (на рисунке они показаны штрихпунктирными линиями) имеет колоколообразную форму и находится в области положительных значений фазы. Рисунок 48 – ЛАЧХ и ЛФЧХ инерционного форсирующего звена при τ>T 3. В каком случае колебательное звено становится консервативным и как при этом изменятся его характеристики? Колебательное звено становится консервативным при  .Переходная характеристика будет иметь вид незатухающих колебаний (рисунок 49) 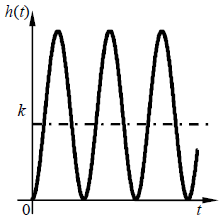 Рисунок 49 – Переходная характеристика консервативного звена Логарифмические частотные характеристики консервативного звена изображены на рисунке 50. Точная ЛАЧХ (сплошная линия) терпит разрыв непрерывности второго рода на частоте сопряжения 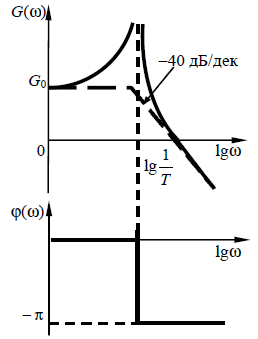 , асимптотическая ЛАЧХ (пунктирная линия) такая же, как у колебательного звена. ЛФЧХ в точке  терпит разрыв непрерывности первого рода (фаза скачком изменяется от 0 до −π ). Рисунок 50 – ЛАЧХ и ЛФЧХ консервативного звена 4. Как нужно изменить схему, приведенную на рис. 51, чтобы получить электронную модель консервативного звена? 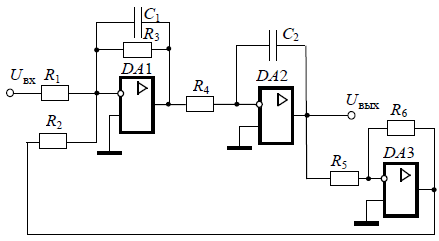 Рисунок 51 – Устройство на операционных усилителях В устройстве, схема которого приведена на рис. 51, в соответствии с формулой: ,получение консервативного звена возможно при 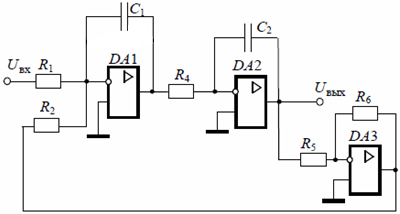 . Для этого резистор  просто нужно удалить из устройства (рисунок 52). Рисунок 52 – Электронная модель консервативного звена 5. Чему равен запас устойчивости по амплитуде в звеньях второго порядка? Запас устойчивости по амплитуде определяется на частоте, при которой ЛФЧХ равна –π. ЛФЧХ звеньев второго порядка асимптотически приближается к значению –π. Откуда получаем, что устойчивости по амплитуде в звеньях второго порядка равен бесконечности. 6. Чем объяснить наличие точки перегиба на переходной характеристике апериодического звена второго порядка? По формуле разложения: 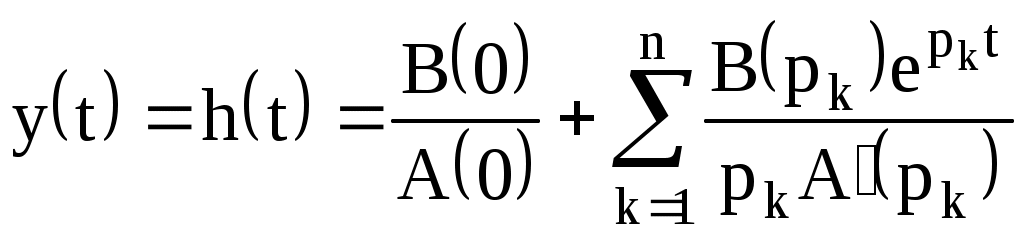 ,получим расчетное выражение для переходной функции апериодического звена второго порядка. Для него:  , , , ,  ,тогда 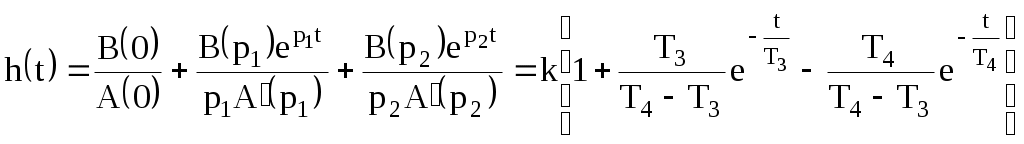 .Наличие точки перегиба на переходной характеристике апериодического звена второго порядка объясняется суммированием двух экспоненциальных составляющих. |
, мс
, %