ТАУ. 1- 6_Лабораторная_ТАУ. Исследование характеристик типовых динамических звеньев сау теория автоматического управления Автор учебнометодического пособия Ю. М. Лебедев Томск 2000 Лабораторная работа 1
 Скачать 233.5 Kb. Скачать 233.5 Kb.
|
|
Федеральное агентство образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) «исследование характеристик типовых динамических звеньев сау» «теория автоматического управления» Автор учебно-методического пособия: Ю.М. Лебедев Томск 2000 Лабораторная работа №1 Вариант №6 Выполнил студент группы « » 2008 г. 2008 Цель работы: получение навыков разработки электронных моделей типовых динамических звеньев САУ, исследование их частотных и переходных характеристик. Программа работы Исследование апериодического (инерционного) звена. 1. Рассчитаем параметры элементов и соберем схему модели апериодического (инерционного) звена. Чтобы выходной сигнал не сдвигался на 180о, нам необходимо последовательно включить еще одну схему пропорционального звена с единичным коэффициентом передачи. k=3; T=60 мс; R2=100 кОм; R1=R2/k=33.3 кОм; C=T/R2=0.6 мкФ. 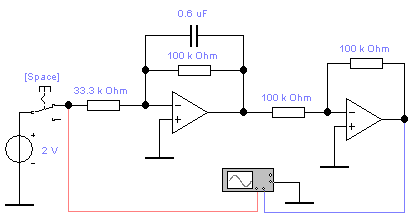 2. Снимем переходную характеристику и определим время переходного процесса tпп. 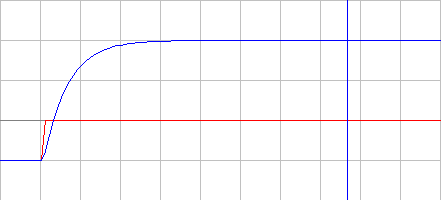 Переходной процесс считается закончившимся при достижении 95% от установившегося значения, т.е. амплитуда сигнала = 6.006 В, 95% = 5.7057 В. Время переходного процесса составляет tпп = 0.185 с. 3. Получим экспериментальные ЛАЧХ и ЛФЧХ, замерим частоту среза ωср и значение фазы φ ср на этой частоте. 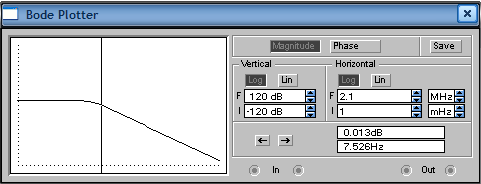 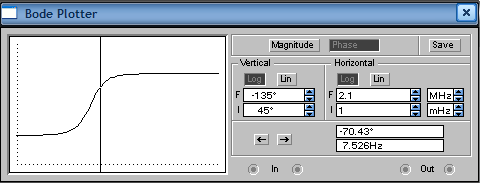 Как видно из рисунков частота среза ωср=2πfср=47.26 Рад/с, а значение фазы φср=-70.43°. 4. Увеличим значения постоянной времени T звена в 2, 3 и 4 раза. Выполним задания п. 2 и 3. Для увеличения T увеличим емкость конденсатора соответственно в 2, 3 и 4 раза. Полученные данные занесем в таблицу:
5. Построим зависимости tпп = f(T), ωср = f(T) и φ ср = f(T).    Исследование инерционного форсирующего звена. 1. Рассчитаем параметры элементов и соберем схему модели инерционного форсирующего звена. Чтобы выходной сигнал не сдвигался на 180о, нам необходимо последовательно включить еще одну схему пропорционального звена с единичным коэффициентом передачи. k=2; T1=60 мс; T2=120 мс; R2=100 кОм; R3= T2/C-R2=100 кОм; R1=R3/k=50 кОм; C=T1/R2=0.6 мкФ. 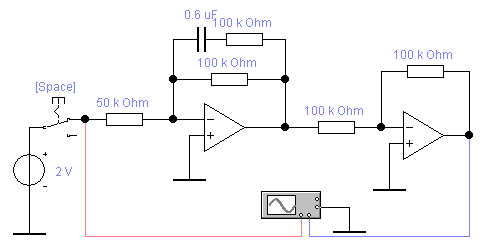 2. Снимем переходную характеристику и определим время переходного процесса tпп. 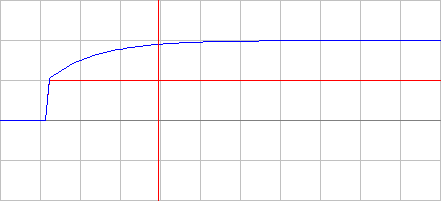 U0 = 2 В, Uуст = 3.8 В. Время переходного процесса составляет tпп = 0.285 с. Параметр λ=(U0/Uуст )*100% =(2/3.8)*100%=52.63% 3. Получим экспериментальные ЛАЧХ и ЛФЧХ, замерим частоту среза ωср и значение фазы φ ср на этой частоте. 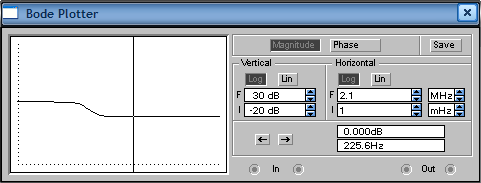 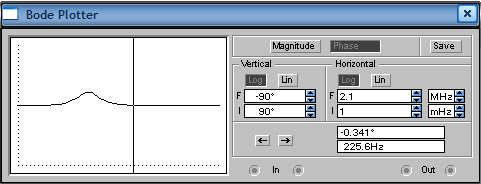 Частота среза ωср = 1416.77 Рад/с, а значение фазы φ ср = -0.34°. Установим соотношения значений постоянных времени T2=3T1, T2=4T1, T2=5T1. Выполним задания п. 2 и 3. Для изменения постоянной времени Т2 изменим значение сопротивления R3, а что бы коэффициент передачи оставался неизменным, изменим также значение сопротивления R1. Полученные данные занесем в таблицу:
5. Построим зависимостиλ = f(T2), tпп = f(T2), ωср = f(T2) и φ ср = f(T2).     Исследование колебательного звена. 1. Рассчитаем параметры элементов и соберем схему модели колебательного звена. k=6; T=35 мс; R2=R5=R6=100 кОм; C1= C2=1 мкФ; ξ=0.7. 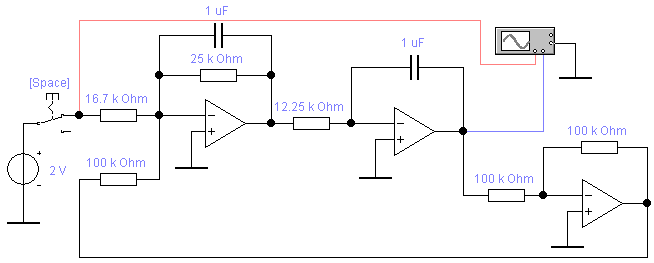 2. Снимем переходную характеристику и определим время переходного процесса tпп, зафиксируем максимальное Uмакс и установившееся Uуст значения выходного напряжения. 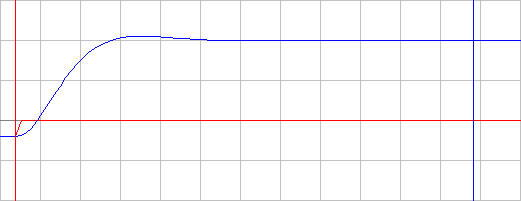 Uмакс = 12.54 В, Uуст = 11.98 В. Время переходного процесса составляет tпп = 0.573 с. 3. Рассчитаем значение перерегулирования. Значение не превышает 5%, следовательно, параметры электронной модели колебательного звена рассчитаны правильно. 4. Получим экспериментальные ЛАЧХ и ЛФЧХ, замерим частоту среза ωср и значение фазы φ ср на этой частоте и определим запас устойчивости по фазе Δφ. 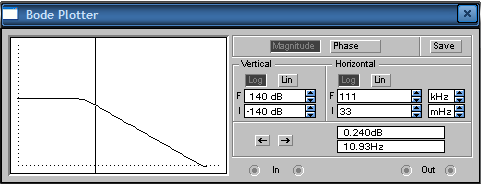 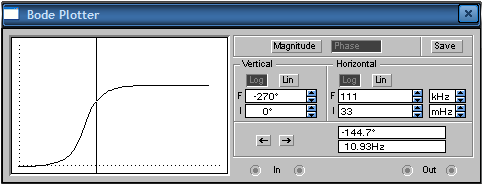 Как видно из рисунков частота среза ωср = 69.08 Рад/с, значение фазы φ ср = -144.7°. Δφ = 180 - │φ ср│= 35.3° 5. Установим значения ξ=0.5, ξ=0.3, ξ=0.1 и повторим выполнение задания п. 2 и 3. Полученные данные занесем в таблицу.
6. Построим зависимости tпп = f(ξ), σ = f(ξ), ωср = f(ξ) и φ ср = f(ξ), Δφ = f(ξ).      Исследование апериодического звена второго порядка. 1. Рассчитаем параметры элементов и соберем схему модели колебательного звена. k=6; T=35 мс; R2=R5=R6=100 кОм; C1= C2=1 мкФ; ξ=1. 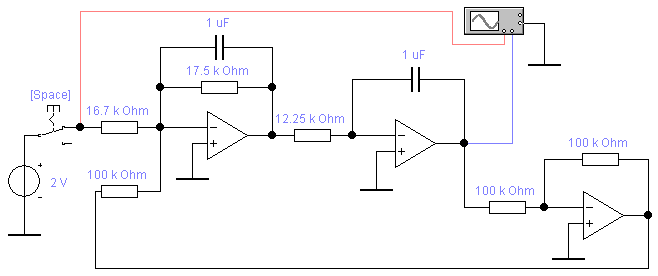 2. Снимем переходную характеристику и определим время переходного процесса tпп. 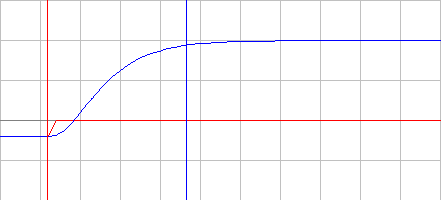 Время переходного процесса составляет tпп = 0.171 с. 3. Получим экспериментальные ЛАЧХ и ЛФЧХ, замерим частоту среза ωср и значение фазы φ ср на этой частоте. 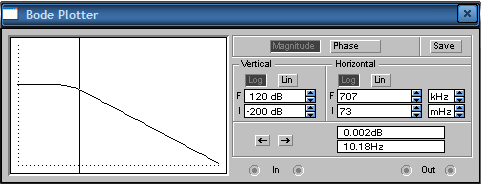 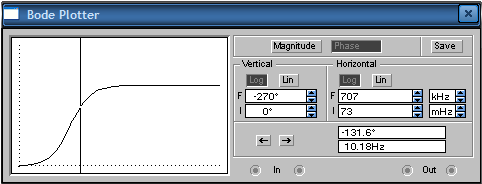 Как видно из рисунков частота среза ωср = 63.93 Рад/с, значение фазы φ ср = -131.6°. 4. Установим значения ξ=2, ξ=3, ξ=4. Выполним задания п. 2 и 3. Полученные данные занесем в таблицу:
5. Построим графики зависимостей tпп = f(ξ), ωср = f(ξ) и φ ср = f(ξ).   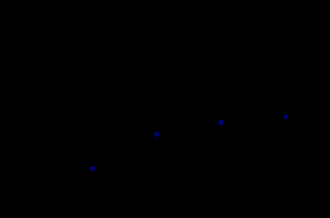 Анализ результатов работы. Влияние постоянной времени на апериодическое звено: - при увеличении постоянной времени увеличивается время переходного процесса, уменьшается частота среза, сдвиг фазы не меняется, т.е. запас устойчивости по фазе не зависит от постоянной времени. Влияние форсирующего звена на инерционное: - увеличивается время переходного процесса, полоса пропускания частот уменьшается снижается запас устойчивости по фазе. Влияние коэффициента демпфирования на колебательное звено: - коэффициент демпфирования колебательного звена увеличивает полосу пропускания частот, время переходного процесса увеличивается, перерегулирование увеличивается, запас устойчивости по фазе снижается. Ответы на контрольные вопросы: - Исходя из экспериментальных данных (график, таблица), можно увидеть зависимость tпп =3T, следовательно постоянная времени T инерционного звена пропорционально увеличивается с увеличением времени переходного процесса tпп. - 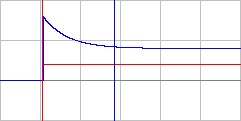 Характеристики изменятся следующим образом: Характеристики изменятся следующим образом:в начальный момент будет скачок напряжения, время переходного процесса уменьшится tпп=0,18с. АЧХ и ФЧХ будут иметь следующий вид: 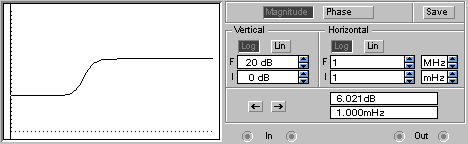 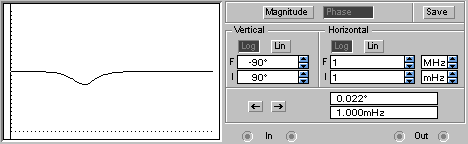 Исчезнет частота среза ωср (т.е. звено будет иметь усилительные свойства на всех частотах). Значение фазы φ сризменяется от близкого к нулю, затем с увеличением АЧХ принимает отрицательное значение, а потом снова близкое к нулю. - Колебательное звено становится консервативным, когда коэффициент демпфирования равен нулю, колебания переходного процесса становятся незатухающими, амплитуда на сопрягающей частоте становится бесконечной, фаза скачком из 0 становится равной -π. - Исключив сопротивление R3-обратной связи первого каскада, получим из колебательного звена консервативное. - Апериодическое звено второго порядка состоит из двух последовательно соединенных апериодических звеньев первого порядка, в связи с этим при суммировании двух экспоненциальных составляющих происходит перегиб. |
