Главная страница
Навигация по странице:

  • Ответ

    		•

    Задача 1 2 Задача 2 7 Задача 3 9 Задача 4 12 Задача 5 18 Список литературы 20 Задача 1


    Скачать 250.17 Kb.
    НазваниеЗадача 1 2 Задача 2 7 Задача 3 9 Задача 4 12 Задача 5 18 Список литературы 20 Задача 1
    Дата15.03.2023
    Размер250.17 Kb.
    Формат файлаdocx
    Имя файлаvar_5.docx
    ТипЗадача
    #993068


    Содержание



    Задача 1 2

    Задача 2 7

    Задача 3 9

    Задача 4 12

    Задача 5 18

    Список литературы 20


    Задача 1



    В момент t = 0 в цепи, схема которой показана на рис. 2.4 (а – варианты 1–4, 27-30; б – варианты 5–8, 23-26; в – варианты 9–12, 20-22; г – варианты 13–19), происходит коммутация. Параметры источника и всех элементов указаны в табл.2.5. Определить токи во всех ветвях в момент коммутации и в установившемся режиме (после окончания переходного процесса), время переходного процесса. Определить функцию переходного тока (напряжения), указанную в табл.2.5 и построить ее график.

    До коммутации:

    - для замыкания ключа S - токи в цепи отсутствовали, конденсатор был разряжен;

    - для размыкания ключа S - цепь работала в установившемся режиме.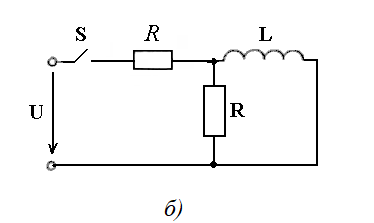



    Таблица 1 – Параметры элементов цепи (задачи 1 и 2)

    № п.п
    Коммутация
    U, В
    С, мкФ
    L, мГн
    RL, Ом
    R, Ом
    Функция

    5
    Размыкание S
    50



    10
    2
    50
    iL(t)



    Решение

    Составим схему замещения после коммутации – рисунок 1.1.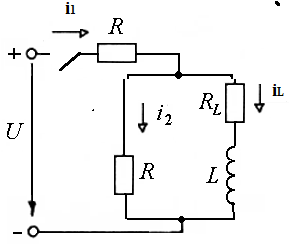



    Рисунок 1.1 – Схема замещения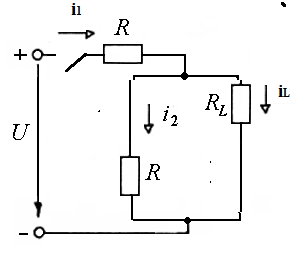



    Рисунок 1.2 – Схема замещения в установившемся режиме

    2. Определим токи в ветвях в момент коммутации.

    Эквивалентное сопротивление цепи равно: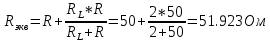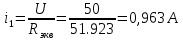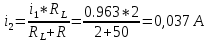









    4. Определим токи в ветвях в установившемся режиме. После окончания переходного процесса токи в цепи будут постоянными, то есть на их величину не влияет наличие в цепи индуктивности – катушка замещается только сопротивлением RL – рисунок 1.2.

    Ток через R:



    Токи в параллельных ветвях:





    Определим временные параметры переходного процесса. Постоянная времени цепи равна: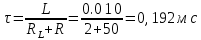



    Время переходного процесса равно: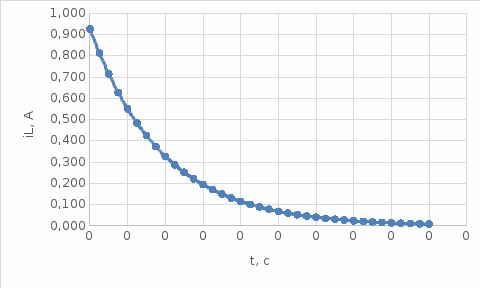







    t, с
    iL(t) A

    0
    0,926

    0,000025
    0,813

    0,00005
    0,714

    0,000075
    0,627

    0,0001
    0,551

    0,000125
    0,483

    0,00015
    0,424

    0,000175
    0,373

    0,0002
    0,327

    0,000225
    0,287

    0,00025
    0,252

    0,000275
    0,222

    0,0003
    0,195

    0,000325
    0,171

    0,00035
    0,150

    0,000375
    0,132

    0,0004
    0,116

    0,000425
    0,102

    0,00045
    0,089

    0,000475
    0,078

    0,0005
    0,069

    0,000525
    0,060

    0,00055
    0,053

    0,000575
    0,047

    0,0006
    0,041

    0,000625
    0,036

    0,00065
    0,032

    0,000675
    0,028

    0,0007
    0,024

    0,000725
    0,021

    0,00075
    0,019

    0,000775
    0,016

    0,0008
    0,014

    0,000825
    0,013

    0,00085
    0,011

    0,000875
    0,010

    0,0009
    0,009


    Ответ:

    токи в момент коммутации: iL(0) = 0.926 А

    i1(0) = 0,963 А

    i2(0) = 0,037 А

    токи в установившемся режиме: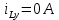

    время переходного процесса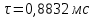

    функция переходного тока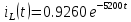



    Задача 2



    В условиях задачи 1 определить переходные токи во всех ветвях операторным методом.



    Рисунок 2.1 – Схема замещения после коммутации
    Составим операторную схему замещения цепи после коммутации – рисунок 2.1.

    Заменим элементы цепи соответствующими операторными изображениями:

    Резисторы R – на резисторы R.

    Резистор RL – на резистор RL.

    Катушка L – на «резистор» с сопротивлением pL и источник ЭДС L*i(0).

    Заменим все известные токи и напряжения операторными токами и напряжениями: для постоянного напряжения U получаем U(р)=U/р.

    В операторной схеме замещения неизвестной является величина iL(0). Для того, чтобы ее определить, проанализируем схему до коммутации.

    Определим начальные условия.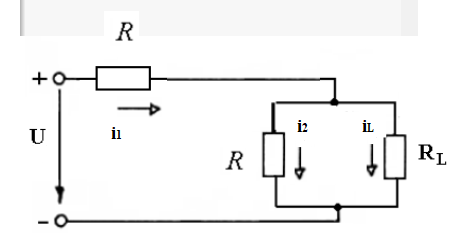



    Рисунок 2.2 – Схема до коммутации
    Эквивалентное сопротивление цепи равно: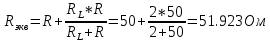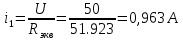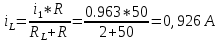









    По первому закону коммутации ток в момент коммутации равен: iL(0) = iL(0-) = 0.926 А

    Составим для схемы, приведенной на рисунке 2.1, уравнение по 2 закону Кирхгофа, описывающее операторную схему замещения, и определим из нее ток в индуктивности: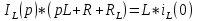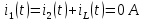











    Задача 3



    Полупроводниковый диод включен параллельно с линейным резистором R, как показано на рис.2.5. Общий ток, тип диода и сопротивление резистора указаны в табл.2.6. Определить токи через диод и резистор.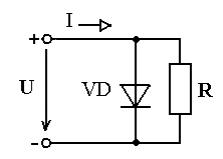



    Рис. 2.6
    Таблица 3 – исходные данные

    № п.п
    Тип диода
    I, мА
    R, Ом

    5
    МД226
    150
    5



    Решение


    1. Составим схему замещения цепи – рисунок 3.1.




    Рисунок 3.1 – Схема замещения


    1. Вычертим в одной системе координат в одном масштабе ВАХ всех элементов цепи.

    ВАХ линейного резистора R представляет собой прямую линию, уравнение которой I = U/R. Для построения такого графика нам понадобятся две точки:

    - начало координат (0, 0);

    - точка, координату U которой выберем произвольно, например, пусть U=0,6 В, тогда вторая точка координат этой точки I = 0,6/5 =120 мА.

    Обозначим график ВАХ резистора 1.

    ВАХ диода найдем в справочнике. Перерисуем ВАХ диода в ту же систему координат, обозначив график ВАХ диода – 2, рисунок 3.2.

    Рисунок 3.2 - ВАХ
    3. Составим уравнение цепи по законам Кирхгофа. Так как задано параллельное соединение элементов, то по 1 закону Кирхгофа:

    I(U) = IR(U) + IVD(U)

    Построим ВАХ цепи в целом. Из уравнения следует, что ВАХ всей цепи I может быть построена суммирование ВАХ резистора и диода – по токам (по ординатам). Построив несколько точек, соединим их плавной кривой линией, получим ВАХ всей цепи 3 - рисунок 3.1.

    4. По заданному общему току цепи I = 150 мА по графику 3 определим напряжение, приложенное к цепи U = 0.494 В.

    Определим искомые токи, протекающие через элементы цепи.

    По ВАХ 1 при U = 0.494 В определим ток через резистор IR = 98.8 мА.

    По ВАХ 2 при U = 0,494 В определим ток через диод IVD = 51.2 мА.

    Сделаем проверку решения.

    Подставим найденные токи в уравнение цепи:

    IR + IVD = 98.8 + 51.2 = 150 мА = I

    Вывод: задача решена правильно. Ток через резистор IR = 98.8 мА, ток через диод IVD = 51.2 мА.

    Задача 4



    Эскиз МЦ изображен на рис. 2.7. Магнитопровод МЦ образован двумя деталями, изготовленными из сталей заданных марок: марка стали А – 3413; марка стали В – 1211 (четные варианты) / 1511 (нечетные варианты). Кривые намагничивания сталей показаны на рис. 2.8. Ширина конструктивного воздушного зазора δ = 0,05 мм. Число витков катушки w = 1000 - №∙2. Определить магнитный поток в магнитопроводе, создаваемый током I = (№ + 50)∙10-3 А (обратная задача).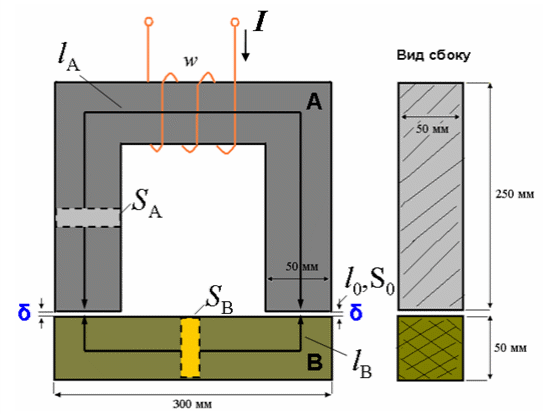



    Рис. 2.7



    Рис. 2.8
    Исходные данные:

    Марка стали А – 3413

    Марка стали В – 1511

    Ширина конструктивного воздушного зазора δ = 0,05 мм.

    Число витков катушки w = 1000 - 5∙2 = 990

    Ток I = (5 + 50)∙10-3 = 55∙10-3 А = 0,055 мА
    Решение
    1. МЦ разбиваем на три участка: участок А из стали 3413, участок В из стали 1511 и воздушный зазор.

    Длины средних магнитных линий из стали и воздушного зазора равны: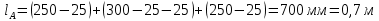







    Площадь поперечного сечения стальных и воздушного участков одинакова и равна:



    2. Определяем магнитное сопротивление воздушного зазора по формуле:



    3. Вычисляем МДС обмотки по формуле: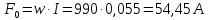



    4. Определяем значение магнитного потока в МЦ в первом приближении. Пренебрегая магнитным сопротивлением стали по сравнению с воздушным зазором с учетом 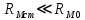, приближенно оценим величину магнитного потока по закону Ома для МЦ:



    5. Реализуем алгоритм последовательного приближения.

    5.1.Решаем прямую задачу расчета МЦ при Ф = Ф1 (т.е. первое приближение МДС цепи).

    Магнитная индукция равна:



    По кривой намагничивания 3413 находим напряженность стали:



    По кривой намагничивания 1511 находим напряженность стали:



    Напряженность магнитного поля в воздушном зазоре:



    МДС обмотки равна: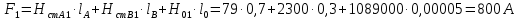



    Сравниваем приближенное значение МДС с истинным значением. Так как F1 > F0, то зададимся новым приближенным значением магнитного потока Ф2 < Ф1.

    5.2. Решим прямую задачу, задаваясь различными значениями магнитного потока Ф, результаты расчетов сведем в таблицу 3.1

    Пусть Ф = Ф2 = 0,25 мВб.

    Магнитная индукция



    По кривой намагничивания 3413 находим напряженность стали: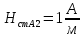



    По кривой намагничивания 1511 находим напряженность стали:



    Напряженность магнитного поля в воздушном зазоре:



    МДС обмотки равна:



    Сравниваем приближенное значение МДС с истинным значением. Так как F2 < F0, то зададимся новым приближенным значением магнитного потока Ф3 > Ф2.

    Пусть Ф = Ф3 = 1 мВб.

    Магнитная индукция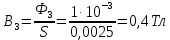



    По кривой намагничивания 3413 находим напряженность стали: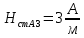



    По кривой намагничивания 1511 находим напряженность стали: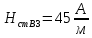



    Напряженность магнитного поля в воздушном зазоре: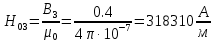



    МДС обмотки равна:



    Сравниваем приближенное значение МДС с истинным значением. Так как F3 < F0, то зададимся новым приближенным значением магнитного потока Ф4 > Ф3.

    Пусть Ф = Ф4 = 1.5 мВб.

    Магнитная индукция



    По кривой намагничивания 3413 находим напряженность стали: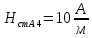



    По кривой намагничивания 1511 находим напряженность стали:



    Напряженность магнитного поля в воздушном зазоре: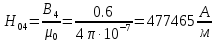



    МДС обмотки равна: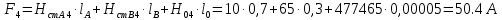



    Сравниваем приближенное значение МДС с истинным значением. Так как F4 < F0, то зададимся новым приближенным значением магнитного потока Ф5 > Ф4.

    Пусть Ф = Ф5 = 2 мВб.

    Магнитная индукция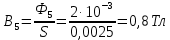



    По кривой намагничивания 3413 находим напряженность стали:



    По кривой намагничивания 1511 находим напряженность стали: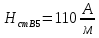



    Напряженность магнитного поля в воздушном зазоре: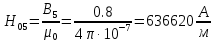



    МДС обмотки равна: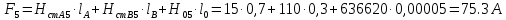



    Сравниваем приближенное значение МДС с истинным значением. Так как F5 > F0, то закончим расчеты.

    6. По результатам расчетов, сведенных в таблицу 3.1, построим график – рисунок 3.3 - вебер-амперную характеристику МЦ.
    Таблица 3.1 – Результаты расчетов

    Ф, мВб
    0,25
    1
    1,5
    2

    F, А
    10.7
    31.5
    50.4
    75.3


    Рисунок 3.3 – Вебер-амперная характеристика МЦ
    7. По графику (рисунок 3.3) определяем при

    искомый магнитный поток: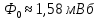
    Ответ: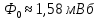

    Задача 5



    Потенциалы обкладок конденсатора, показанного на рис. 2.9, равны V1 = № + 10 B, V2 = -V1. Расстояние между обкладками d = № + 5 мм. Считая, что потенциал изменяется только в направлении, нормальном к обкладкам, определить законы изменения потенциала и напряженности поля.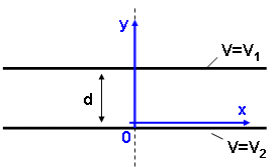



    Рис. 2.9
    Исходные данные

    V1 = 5 + 10 = 15 B

    V2 = - 15 В.

    d = 5 + 5 = 10 мм
    Решение
    Потенциал изменяется только вдоль координаты y, поэтому уравнение Лапласа принимает вид:



    После интегрирования находим: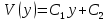



    Постоянные С1 и С2 определим из условий:

    при у = 0 V = V2

    при у = d V = V1

    Подставим данные значения: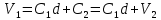







    Таким образом:



    Воспользуемся тем, что характеристики поля, напряженность и потенциал, связаны между собой уравнением:
    .

    Запишем данное уравнение для одномерного случая и рассмотрим поведение потенциала в областях на пластинах 1 и 2 и между пластинами:




    Знак минус указывает на то, что вектор напряженности полня направлен в сторону уменьшения потенциала точек поля.
    Ответ: закон изменения потенциала

    Закон изменения напряженности поля




    Список литературы



    1. Бессонов, Л. А. Теоретические основы электротехники. Электрические цепи [Текст]: учебник / Л. А. Бессонов. – М: Гардарики, 2016. – 701 с.

    2. Оробинский, А. М. Теоретические основы электротехники [Текст]: учебник / А. М. Оробинский, А. В. Лучин, Ю. В. Раменский. – Серпухов: ФВА РВСН, 2019. – 275 с.

    написать администратору сайта