Нелинейность роста знаний. 1. История науки по Т. Куну Допарадигмальный период
 Скачать 138.18 Kb. Скачать 138.18 Kb.
|
|
Содержание Введение 1. История науки по Т.Куну 1.1. Допарадигмальный период 1.2. Зрелая наука 2. История зрелой науки 2.1. Нормальная наука 2.2 Аномалии и кризис в науке 2.3. Революция в науке 2.3.1 Несовместимость старой и новой парадигмы 2.3.2 Переключение гештальта в результате революций 2.3.3 Выбор новой парадигмы. 3. О характере революции в математике 3.1. Основные точки зрения на революцию в математике 3.2 Математика и научные революции Заключение Литература Введение Наука и техника XX века поставили перед методологией науки актуальную проблему анализа природы, структуры тех коренных изменений научного знания в науке. Они называются революциями наук. На Западе интерес к этой проблеме был вызван появлением в 70-х годах работы Томаса Куна «Структура научных революций». Книгу Т.Куна, которая вызвала огромный интерес историков науки, но также философию и психологию в различных странах мира, а также многих естествоиспытателей разных стран. Эта книга не только содержит достаточно спорный взгляд на развитие науки, но и написана весьма спорно. Если Кун не открывает ничего нового, то многие авторы говорили об отсутствии в развитии науки нормальных и революционных этапов. Они не смогли найти аргументированного ответа на вопросы: «Как отличить небольшие, постепенные изменения от изменений коренных, качественных и революционных?»?„Что происходит с этими процессами в предшествующий период?“. И это не случайно, поэтому история науки часто представляется как простой перечень фактов и открытий. В этом случае прогресс в науке сводится к простому накоплению и росту научного знания (кумуляции), что не раскрывает внутренние закономерности происходящих изменений. С этим подходом столкнулся Кун в своей книге, критикуя его концепцию развития науки через периодически происходящие революции. Кратко теорию К. Куна можно описать так: периоды спокойного развития (период «нормальной науки») сменятся кризисом, который может быть разрешен с помощью революции и замены доминирующей парадигмой в будущем. Кун определяет парадигму как совокупность понятий, теории и методов исследования. Эта система дает научному сообществу модель постановки проблем и их решения. Из-за попытки наглядно представить изучаемую теорию читателям предлагается схематический график развития науки по Куну. В данном случае речь пойдет о том, что будет описано далее – о понятии и процессах, которые изображены на схеме. 1. История науки по Т.Куну Т.Кун в своей книге «Структура научных революций» описывает историю науки следующим образом: 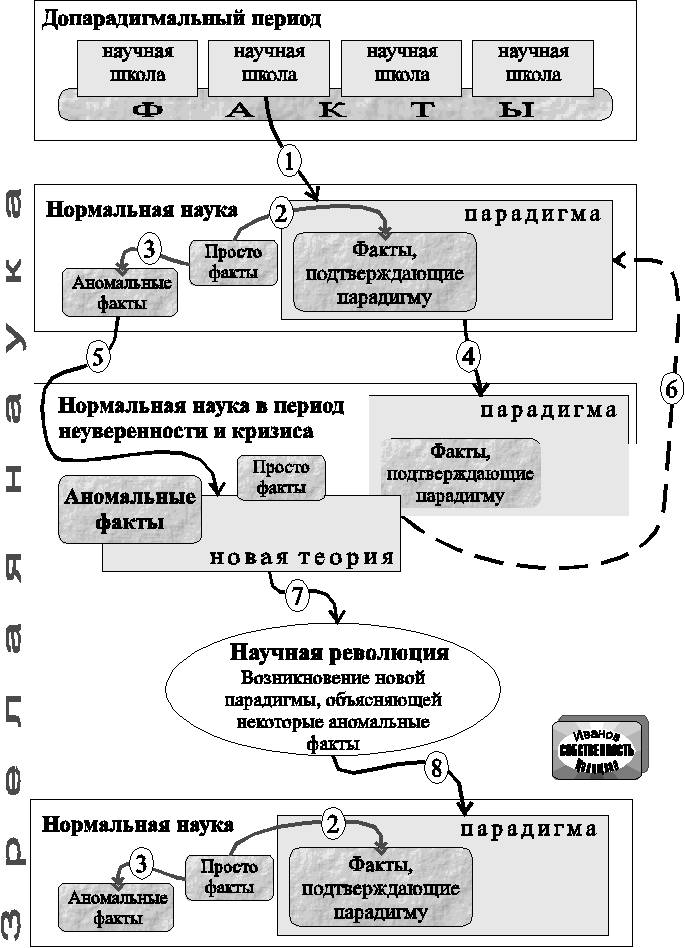  1.1 Допарадигмальный период Приблизительно допарадигмальный период развития науки характеризуется наличием большого количества школ и направлений. Все школы имеют разные интерпретации различных явлений и фактов, лежащих в русле определенной науки. В основе этих интерпретаций могут лежать различные методологические или философские предпосылки. Если говорить о физике, то в качестве примера можно привести историю физической оптики. В период от глубокой древности до конца XVII века не было периода, в котором бы была одна и общепринятая точка зрения на природу света. Кроме того, существовало множество противоборствующих школ. Большинство из них придерживалось какой-либо разновидности теории Эпикура и Аристотеля или Платонов. Направление, которое рассматривает свет в качестве частиц материального тела, рассматривало свет как модификацию среды между телом и человеческим глазом; кроме того, свет объяснялся в терминах взаимодействия среды с излучением глаз. Даже если все эти школы физической оптики до Ньютона были учеными, результат их деятельности не является научным. При отсутствии единой основы для своих убеждений, представители каждой школы пытались построить свою собственную физическую оптику заново, начиная с наблюдений. Научные работники не обращались к коллегам, а скорее к оппонентам из других школ в данной области исследований и ко всем, кто интересуется предметом их исследования. По мнению современных ученых, их работы можно отнести к категории научно-популярных изданий. По словам Курта Куна, допарадигмальный период – это время возникновения любой науки. Описанная выше ситуация характерна для развития каждой науки, прежде чем эта наука выработает свою первую всеми признанную теорию и методологию исследований. Кун называет это парадигмой. Начиная с начала становления любой науки различные ученые сталкиваются со схожими категориями явлений. Однако они не всегда одинаково описывают и интерпретируют одни и те же явления. По мнению ученых, исключение составляют такие науки, как математика или астрономия, в которых первые прочные парадигмы относятся к их предыстории. Другие дисциплины могут возникнуть на стыке уже сформировавшихся отраслей знания. Вместе с тем, начало астрономии характеризовано «многопарадигмальностью». Первые парадигмы появились в таких разделах биологии, как, например, учение о наследственности. Это произошло только в XX веке. Зрелая наука Как считает Кун, на смену допарадигмальной науки идет, по его мнению, зрелая наука. В современной науке существует не более одной общепринятой парадигмы. В начале развития науки существуют существенные расхождения, которые возникают с появлением общих теоретических и методологических предпосылок или принципов. Затем они постепенно исчезают в значительной степени, а затем и окончательно. Обычно их исчезновение связано с успехом одной из допарадигмальных школ, например парадигмы Франклина в области исследования электрических явлений. Существует парадигма, в которой можно определить область исследований и более четкое определение области исследования. С принятием этой концепции школьная школа, которая интересовалась природой из простого любопытства, становится профессиональной научной школой, а предмет ее интереса превращается в научную дисциплину. Сейчас мы можем изложить в учебниках такие парадигмы или научные достижения, которые долгое время признавались определенным научным сообществом как основа для развития его дальнейшей деятельности. В учебниках разъясняется сущность принятой теории, показываются многие ее применения и сравниваются эти результаты с типичными наблюдениями и экспериментами. Именно они определяют права и методы исследования каждой области науки для будущих поколений ученых. [1][2] После того как эти книги стали общепринятыми, аналогичную функцию выполняли известные классические труды ученых: «Начало» и "Оптика», электрическое электричество Франклина. Лавуазье. Их появление - это уникальный случай, который может на долгое время отвратить ученых к конкурентным концепциям. Они были достаточно открыты для нового поколения исследователей и могли в их рамках найти решения проблем любого типа. 2. История зрелой науки На протяжении всего своего развития наука проходит несколько этапов. При этом период нормальной науки сменяется кризисом. Он или разрешается методами нормализованной науки, либо приводит к научной революции в рамках парадигмы. С новой парадигмой вновь наступает период нормальной науки. При этом, согласно концепции Куна, развитие науки происходит не за счет постепенного увеличения новых знаний на старые знания и замены основных представлений -- через периодические научные революции. Кун считает, что действительного прогресса в области объективной истинности научных знаний не существует. Он полагает, что такие знания могут быть определены только как более или менее эффективные для решения соответствующих задач, а не как истинные или ложные. В этой связи следует отметить, что Кун не связывает явно смену парадигм с преемственностью в развитии науки, с движением по спирали от неполного знания к более полному и совершенному. Мне кажется, Кун не рассматривает вопрос о качественных соотношениях старых и новых парадигм: является ли новая концепция лучше старой с точки зрения прогресса в научном познании? Прогресс науки у Куна не направлен вверх к высотам «абсолютной истины», он сложился стихийно в ходе исторического развития наук. Два. Спокойная наука "Нормальной наукой" Кун называет исследование, прочно опирающееся на одно или несколько прошлых научных достижений, которые в течение некоторого времени признаются определенным научным сообществом в качестве основы для развития, то есть это исследование в рамках парадигмы и направленное на поддержание этой парадигмы. В результате при ближайшем рассмотрении «создается впечатление, что природу пытаются втиснуть как будто бы во временную и довольно узкую коробку», «явления, которые не могут поместиться в эту коробку, часто вообще упускаются из виду». По этой причине нормальная наука не ставит перед собой цель создания новой теории, и успех в нормальном научном исследовании заключается совсем не во всем этом. Изучение нормальной науки направлено на разработку тех явлений и теорий, существование которых предполагается парадигмой. Коротко деятельность ученых в рамках нормальной науки можно описать как наведение порядка (ничего не революционного). Это ни в коем случае не революция. По мнению К. Куна, три вида задач -- установление значимых фактов и сравнение фактов с теорией - исчерпывают... Нормальной наукой является то поле, в котором она существует.2 1. Большинство проблем, поднятых даже самыми выдающимися учеными, обычно охватывается этими тремя категориями. Кроме того, существуют и другие экстраординарные проблемы, но они возникают только в особых случаях. Зависимость между работой и парадигмой невозможна, поэтому отказаться от нее означает прекратить те научные исследования, которые она определяет. Если мы откажемся от парадигмы, то мы придем к научной революции. Определение «нормальной науки», введенное Куном, было подвергнуто острой критике со стороны сторонников критического рационализма во главе с Карлом Попперым. Поппер считает, что нормальная наука существует. Но если Куну это явление кажется нормальным, то Поппер в работе «Нормальная наука и ее опасности» (1970) рассматривает его как опасный для науки в целом. Первое направление – это критика понимания Куном нормальности науки. Первое – это абсолютное отрицание самой возможности возникновения науки. В этом смысле наука никогда бы не смогла продвинуться, если основной деятельностью ученых была нормальная наука. Противники этого направления полагают, что нормальной науки с кумулятивным накоплением знания не существует; что из нормальной науки Куна невозможно вырастить революцию. “Нормативная” наука, как правило, ассоциируется с «стагнацией» в науке. С критикой нормальности в области науки выступил Карл Поппер. Его признание в том, что есть нормальная наука, но при этом он умалчивает о ее роли. У Поппера есть мнение о том, что нормальная научная работа Куна может быть опасна для самого существования науки. В глазах Поппера «нормальный» ученый выглядит жалким: он не привык к критическому отношению. В действительности, если ученый работает в рамках какой-то теории, он может выйти за эти рамки в любой момент. По мнению Поппера, неверно говорить о истории науки как о непрерывной революции и принижать роль нормальной науки в науке. Конечно же, в понимании Куна «самая удивительная особенность проблем нормальной научной мысли». У них очень мало шансов на большие открытия, будь то открытие новых фактов или создание новой теории"3 2. При этом ученые, которые следуют норме науки, не ставят перед собой цели создания новых теорий или каких-то значительных качественных (революционных) изменений в своей научной дисциплине. Им важно знать, что результаты научного исследования расширяют область применения парадигмы и добавляют некоторые параметры. В математике такие результаты могут быть предсказаны, но сам способ получения результата или доказательства остается в значительной степени сомнительным. Большинство проблем трудно решить, хотя предшествующая практика нормальной науки давала все основания считать их решенными или почти полностью разрешеными в силу существующей парадигмы. Решение проблемы исследования требует решения множества сложных инструментальных, концептуальных и математических задач. В этом случае, нормальная наука предстает у Куно как “решение головоломок”. Учёный, преуспевший в этом, становится специалистом своего рода по решению задач-головоломок, и стремление к разрешению все новых и новых задач-головоломок является стимулом его дальнейшей активности. Наиболее важными мотивами, которые побуждают к научному исследованию, можно назвать желание решить головоломку или задачу, которую до него не решал никто или в решении которой никто из участников был убедительным. При этом работа в рамках парадигмы предполагает, что научное сообщество с приобретением парадигмы получает критерии для определения проблемных ситуаций и может считать их теоретически разрешимыми, пока эта концепция признана общепризнанной. В большинстве случаев ученые занимаются только проблемами, которые сообщество считает научными или заслуживающими внимания. Даже изолировать научное сообщество от тех важных проблем, которые невозможно свести к типу головоломок из-за отсутствия концептуального и инструментального аппарата парадигмы. [1] Некоторые проблемы могут быть отброшены только потому, что они кажутся слишком серьезными, чтобы тратить на них время. По мнению Куна, одна из причин кажущегося прогресса в развитии нормальной науки заключается в том, что ученые фокусируются на проблемах с нехваткой изобретательности. 2.1. Нормальная наука Нормальная наука не ставит своей целью нахождение нового факта или теории, тем не менее, новые явления вновь и вновь открываются научными исследованиями, а радикально новые теории опять и опять изобретаются учеными. В первую очередь открытие начинается с осознания аномалии. Это означает, что природа каким-то образом нарушила ожидания, которые были заложены в парадигму нормальной науки".4Написала Кун в "Круге. Такое понимание различия в новых фактах и теории может привести к более или менее расширенному изучению аномалии. Но если в рамках этой парадигмы аномалия не возникает, то она может возникнуть на фоне другой парадигмы. Если парадигма точна и развитая, она выступает более чувствительным индикатором при обнаружении аномалии, что в свою очередь приводит к изменению парадигмы. Установление аномалии - это период, в течение которого парадигмальные теории адаптированы к новым обстоятельствам до тех пор, пока аномалия не станет ожидаемой. Для усвоения теории нового вида фактов необходимо что-то большее, чем простое дополнение теории; ученый должен научиться видеть природу в ином свете. И это изменение парадигмы потребовалось для того, чтобы восприятие аномалии изменилось. У всех известных открытий новых видов явлений есть три общих черты: предварительное осознание аномалии, постепенно или мгновенно ее признание и последующее изменение парадигмальных понятий. При осознании открытия научное сообщество может объяснить более широкую область явлений и процессов или более точно описать те явления, которые ранее не были известны. В этом случае можно добиться этого только путем удаления определенных убеждений из прежней парадигмы. Разберем несколько примеров о том, что осознание аномалии стало предпосылкой для значительных изменений в теории естествознания. Уравнение результатов измерений положения планет с помощью геоцентрической системы Птолемея и их предсказания, полученного при помощи географического представления о планете, привело к самому известному в истории естествознания изменению парадигмы - появлению астрономии Коперника. Новое понимание света и цвета Ньютона появилось с открытием того, что ни одна из существующих парадигм не может учесть длину волны спектра. Эта новая волна появилась в результате возрастающего интереса к аномалиям, затрагивающим дифракционные и поляризационные эффекты теории Ньютона. [1] Необычные противоречия в теории множеств и логики (первые парадоксы, или антиномии были обнаружены еще Г.Кантором) вылились кризисом оснований математики в начале XX века и появлением новых теорий и концепций. Понимание аномалий обычно длится настолько долго и проникает так глубоко, что можно с полной уверенностью сказать: область в которой они были обнаружены, находится в состоянии нарастающего кризиса. В качестве кризиса Кун понимает постоянную неспособность нормальной науки решать свои головоломки в той мере, как она должна это делать. Тем более возникающие в науке аномалии вызывают резко выраженную профессиональную неуверенность в научной среде. Кун говорит, что банкротство существующих правил означает начало поиска новых.7. Так, в результате нарастающего кризиса возникает множество новых теорий или, по Куну, «новая теория предстает как непосредственная реакция» на кризис.5. О том, что на ранних стадиях развития новой парадигмы можно создать альтернативные теории, свидетельствует история науки. Не так ли? Как отмечает Кун, философы науки неоднократно демонстрировали способность возводить более чем один теоретический конструкт на одном и том же наборе данных. Однако учёные редко пользуются этим изобретением альтернатив, характерным для допарадигма. Как в производстве, в науке смена оборудования -- крайняя мера. Она применяется лишь по неотложным причинам. Кризисы являются индикаторами своевременности этого переоборудование. По сути любой кризис начинается с сомнения в существующих парадигмах и последующего разрушения правил исследования в рамках нормальной науки. На этом основании исследование во время кризиса похоже на исследование в допарадигмальном периоде, но ученые сталкивались с большими трудностями. И в этот момент все кризисы заканчиваются одним из трех вариантов. По крайней мере в некоторых случаях нормальная наука доказывает свою способность разрешить проблемы, порождающие кризис (этому соответствует пунктирная стрелка 6 на схеме). На самом деле решение проблемы может быть, но не предвидится, поэтому даже радикально новые подходы не помогут. Сфера проблемы откладывается в сторону (в разряд необоснованных аномальных фактов), надеясь, что ее решение будет найдено новым поколением ученых или с помощью более совершенных методов. Возможно также и третье разрешение кризиса, которое может быть достигнуто с возникновением новой теории для объяснения аномалий и борьбой за ее принятие в качестве парадигмы (на схеме этому случаю соответствует процесс обозначенный стрелками 5, 7, 8). Именно этот последний способ завершить кризис Куна и называет его научной революцией. 2.3. Революция в науке Научная революция, в отличие от периода постепенного накопления (кумуляции) знаний, рассматривается как такой некумулятивный эпизод развития науки, во время которого старая парадигма замещается полностью или частично новой парадигмой, несовместимой со старой. Понимание кризисного состояния в предыдущем разделе – это предпосылка революции. В период политической революции выбор между конкурирующими политическим и научным институтами оказывается выбором между несовместимыми моделями жизни общества. Это происходит во время научных революций, когда люди выбирают разные модели жизни научного сообщества. По мнению Куна, выбор не обусловлен и не может быть детерминирован просто оценочными характеристиками процедур нормальной науки... И когда они входят в русло споров о выборе парадигм... В каждой группе есть своя собственная парадигма для аргументации в защиту этой же самой парадигмы.9 7. Кун полагает, что доводы о выборе какой-либо определенной парадигмы «не имеют отношения к логике, а к убеждению». Кюн показал, что научные революции не являются кумулятивным этапом развития науки. Напротив: они считаются кумулятивным этапом в развитии науки.Только лишьНаучная деятельность в рамках нормальной науки может быть проведена благодаря умению ученых отбирать разрешимые задачи-головоломки. 2.3.1 Несовместимость старой и новой парадигмы Научные революции Куна не разделяют позицию позитивистов, которые считают, что каждая новая теория не должна вступать во противоречие с предшествующей теорией. Самым известным примером для защиты такого понимания развития науки является анализ отношения между динамикой Эйнштейна и уравнениями динамики, вытекающими из «Математических Начал Натуральной Философии» Ньютона. Для теории Куна это совершенно несовместимые две концепции: "теория Эйнштейна может быть принята только при признании того, что теория Ньютона ошибочна". Можно ли, в самом деле, динамику Ньютона вывести из роялистской динамики? ... Покажем некоторые. Это те самые «законы» теории относительности, которые были сформулированы Эйнштейном и подтверждены экспериментально. Предложения, содержащие переменные или характеристики отображения пространства и параметров изображения пространственных координат в пространстве с помощью логики и математики дедуцируют еще один ряд предложений... Если я хочу доказать адекватность ньютоновской механики как частного случая, мне нужно добавить к предложениям и так далее. Таким образом, это является передержкой и в следующем. Но есть предложения, специальный случай законов релятивистской механики, но все же они не являются законами Ньютона. Как правило, в серии предложений содержатся переменные и параметры, которые в серии предложений и для представления теории Эйнштейна, обозначают пространственные координаты и время. Масса также содержится в этом документе. Все-таки эти объекты представляют собой эйнштейновское пространство, масса и время. Это означает что физическая сущность Эйнштейна не совпадает с значением ньютоновских понятий, хотя и называется они одинаково... В случае если я не изменю, определения переменной в тексте. Эти предложения мне кажутся ньютоновскими, но они не являются ньютоновскими. В этом случае мы не можем сказать, что они изменены, вышли законы Ньютона... законы физики. Безусловно это объясняет, почему законы Ньютона казались пригодными для работы. Однако, хотя устаревшая теория может рассматриваться как частный случай ее современного преемника, она должна быть преобразована. Также в данной работе, автор приводит другие примеры несовместимости предыдущей и последующей теорий (доньютоновское представление о движении или теория Ньютона, скачок изучения электрических явлений после 17 века). 2.3.2 Переключение гештальта в результате революций По мере развития науки меняются взгляды научных работников на мир. В каком-то смысле можно сказать, что в результате революции ученый оказался совсем в другом мире, разительно отличающемся от прежнего. Вследствие этого, исследователи смотрят на мир сквозь призму парадигмы. У Куна есть сравнение изменений взглядов ученых в результате научной революции с переключением зрительного гештальта: «То, что казалось ученым уткой до и после Революции было кроликом». Гештальт-экспериментальные исследования предполагают, что предпосылкой самого восприятия является некоторый стереотип, напоминающий парадигму. По этой причине исследователи не в состоянии переключать свое восприятие на ту или иную сторону так легко, как это происходит с испытуемыми в гештальт-экспериментах. Например, в работе Кун приводится много примеров такого "изменения виденье мира" в результате научных революций. За счет этого изменения в мире электричества произошли от теории распространения световых волн через эфир к электромагнитной модели Максвелла. Это также замена геоцентрической системы астрономии гелио-геостатическим учением Коперника и т.д. Чаще всего изменения в взглядах скрываются за тем, что после смены парадигмы не произошло заметного со стороны изменений терминологии наук. Однако при внимательном рассмотрении оказывается, что в старые понятия вложен новый смысл. Таким образом, понятие планеты отличается от понятия планет у Ньютона. Так же как время Эйнштейна не равно времени Птолемея. Об этом выше было сказано, что выбор между конкурирующими парадигмами не может быть решен средствами нормальной науки. Все научные школы будут защищать свои точки зрения, чтобы видеть мир через призму своей парадигмы. При таком обсуждении выясняется, что каждая парадигма более или менее удовлетворяет критериям критериев своих оппонентов и не соответствует некоторым критериям, которые определяются ее противниками. 2.3.3 Выбор новой парадигмы При выполнении задачи-головоломки ученый может опробовать множество альтернативных подходов, но он не проверяет парадигму. Попробовать парадигму можно лишь после упорных попыток решить какую-либо проблему (что соответствует началу кризиса) и появления альтернативной теории, претендующей на роль новой парадигмы. В обсуждении выбора новой парадигмы Кун полемизирует с философскими теориями вероятностной верификации. [1] "Один из" Теории требуют сравнения данной научной теории со всеми другими, которые можно считать соответствующими одному и тому же набору наблюдаемых данных. Еще одна задача заключается в мысленном построении всех возможных проверок, которые данная научная теория может пройти. «Каким образом можно было бы осуществить такое построение?» — вот вопрос, который возникает у каждого, кто задумывается над этим. В то же время, Кун выступает и против теории фальсифицирования К.Р.Поппера : «роль…. Совпадение, во многом похоже на роль, которую в этой работе отвели аномальному опыту, то есть опытам, которые вызывают кризисы, готовят путь для новой теории. Тем более это не может быть фальсифицирующим опытом. На самом деле не думаю, что есть еще один в природе…. Эта теория никогда не решает все головоломки в данный момент, а также нет ни одного решения совершенно безупречного. Кун объединил в своей теории обе теории: как теорию фальсификации, так и теорию верификации. Одна из конкурирующих парадигм – это теория фальсификации, которая в свою очередь является соперничающей с существующей. Когда новая парадигма победила, начинается процесс верификации, который состоит в триумфальном шествии новой концепции по развалинам старой. В некоторых случаях новая парадигма выбирается не на основе сравнения возможностей различных теорий в решении проблем. Здесь аргументы в защиту парадигмы будут направлены на «индивидуальное ощущение удобства, эстетическое чувство». Эта новая теория должна иметь больше удобства и простоты в использовании. По мнению Кун, такие аргументы более эффективны для решения математических задач, чем в других естественных науках. 3. О революции в математике В связи с появлением книги Т.Куна «Структура научных революций», опубликованной в русском переводе 1975 г., интерес к проблеме анализа тех коренных изменений в развитии научного знания, которые принято называть революциями науки, возник и у нас на Западе закономерно возникает вопрос о революции математики. Как первая попытка критически оценить идеи Куна по отношению к развитию математики, она была сделанна Г.Мартенсоном в международном журнале "История математического знания". С помощью этих публикаций можно было высказать самые крайние точки зрения на революцию в математике, начиная от полного отрицания и заканчивая частичным признанием. Основные точки зрения на революцию в математике Занимаясь вопросами о характере изменений, происходящих в развитии математического познания и рассматривая их как количественные - постепенные или медленные изменения. Именно поэтому прогресс научного знания заключается в том, чтобы накапливать все больше и больше новых знаний. Такой подход к развитию науки называют кумулятивным. Что касается математики, то ее развитие определяется только чисто количественным ростом нового знания (открытие новых понятий и доказательство новой теоремы); при этом предполагается, что старые понятия и теории не будут пересмотрены. Куан в своей работе решительно критикует такую точку зрения кумулятивного развития научного знания. Несмотря на свою ограниченность, кумулятивистская концепция часто встречается в математике. Не стоит объяснять это просто тем, что в силу самой природы математического познания ученый не обращается непосредственно к наблюдениям и экспериментам. Основой для изучения математики является математика, которая базируется на абстрактно-логической основе. Однако в естествознании это не так. Иногда эксперимент полностью опровергает теорию и требует пересмотра старого научного знания или даже отказа от него. Так как именно на этом базируются попытки отрицания любых революционных изменений в математике. Также следует отметить ошибочность представлений о том, что революция есть полное уничтожение и разрушение старого. Исходя из этой концепции, американский историк математики М.Кроу утверждает следующее: "Необходимой характеристикой революции является то, что какой-либо объект (будь это король или конституция) должен быть отвергнут и безвозвратно отброшен".19. С помощью этого определения он заявляет в своем десятом законе, что революции никогда не случаются на математическом языке. Революция в математике не означает отбрасывания старых объектов, но меняет их смысловое значение и объем (области применимости). В частности, Фурье в своей «Аналитической теории тепла» писал, что математика сохраняет все принципы, которые она приобрела. В другом знаменитом математике Г.Ганкель утверждал, что в большинстве наук одно поколение разрушает то, на что было построено другим... Только в физике каждое поколение создает новую версию истории, основанную на старых структурах. Какое возможно развитие науки, если бы оно состояло в простом отбрасывании старых теорий? Но даже в науке, появление теории относительности и квантовой механики не привело к полному отказе от классической физики Галилея-Ньютона. Только точно указало границы ее применимости. При этом преемственность между старым и новым знанием выражена значительно сильнее, к тому же в математике теории не могут опровергаться экспериментальными методами. В данном случае речь идет о том же самом примере, который приводит Кроу – открытии неевклидовых геометрий. С точки зрения его понимания, это не была революция в геометрии, поскольку Евклид был отвергнут и стал царствовать вместе с другими, неевклидовыми геометриями. Есть некоторые ученые полагают, что революции возможны лишь на основе прикладной математики - в областях использования математических методов для решения прикладных задач. Теории "чистой" математической теории могут оказаться неэффективными для решения прикладных проблем и поэтому могут быть забыты или полностью отброшены. Конечно же, коренные изменения в теориях и методах использования математики являются результатом изменений, произошедших в теоретической математике. Между теоретической и практической математикой существует тесная взаимосвязь, взаимное влияние и сотрудничество. Потому что если мы допускаем революцию в прикладной математике, то должны признать ее существование и во всей теоретической математической системе. [1] Большинство сторонников другой точки зрения на революцию в математике связывают ее с процессами, которые происходят вне рамок самой науки или же относятся к технике математических вычислений и преобразований (формулы и алгоритмы) или философии математики. К тому же именно такого рода революционные перевороты в математике признаются Кроу. Изменения в символике или философском обосновании математики более заметны, чем изменения самой математики. Они происходят на надстройке математической системы и не являются первичными по своей сути. [2] Как правило, это происходит в методологии и философии математики, когда открытие принципиально новых понятий теории или метода приводит к пересмотру учениками их методов. Разрушение канторовской теории множеств и возникновение парадоксов привели к новому стилю мышления в математике, принципам обоснования ее теорий и новым определениям исходных понятий. На этом основании многие взгляды основаны на предположении, что никакие качественные изменения в развитии математики не происходят. В частности: Все развитие математики сводится к простому накоплению и росту знаний: ничего в ней не переоценивается, а сохраняется нетронутым. По началу кажется, что в математике прогресс осуществляется исключительно кумулятивным способом. Такие кумулятивные представления о развитии научного знания и противостоят Томасу Куну. Как и в других науках, количественные изменения (по Куну) в математике так же как и в других областях, в конце концов сопровождаются коренными переменами - научной революцией. 3.2 Математика и научные революции Одним первым мыслителем в истории человечества, который поднял вопрос о научных революциях, был и есть Иоганн Кант. Как он писал. "Примеры математики и естествознания, которые в результате быстрой революции стали тем, что они есть сейчас", достаточно интересны для размышления о сущности той перемены способа мышления, которая оказалась столь благоприятной. По мнению Канта, именно в математике и в естествознании произошли революции. Какая была главная идея у революционной ситуации в математике? В истории математики самые крупные революции в основном связаны с расширением и расширением области их применения, а также увеличение абстрактности глубины, благодаря чему математика точнее отражает действительность. И поэтому это потребует коренного, качественного изменения концептуальной структуры математики. Я думаю, что первая революция в математике связана с переходом от полуэмпирических методов древних египтян к теоретической математике древних греков. В Канте связывал научную революцию со введением доказательств теоремы о равнобедренном треугольнике Фалесом. В период до Фалеса математика представляла собой свод правил, которые определяют площадь фигуры и объем пирамиды. Такой характер носило математическое знание в Египте и Вавилонии. Фалес задал вопрос о доказательствах математических утверждений и тем самым построил единую логически связанную систему. Установление системного подхода при помощи доказательств от одного положения к другому стало новым типом греческой математики. Наука сформировалась как наука, кроме того математика была включена в философию дедуктивным методом рассуждений. Следующая крупная революция в математике относится к XVII веку, и она связана с переходом от постоянных к изучению переменных величин. В. Декарту пришла идея Декарта, которая заменило высказываемое Аристотелем утверждение о том, что математике не нужно изучать только неподвижные предметы. В этом случае можно выделить меру и отношение (цит. по ). На основании [4], с. 117. В своей работе о революции Ф.Энгельс писал: "Поворотным пунктом в математике является Декартова переменная величина". Поэтому в математику вошли движение и диалектика, поэтому для нее необходимо дифференциальное исчисление.22. В этот период возникли новые понятия переменной, производной и дифференциала, которые отсутствовали в прежней математике. С помощью этих понятий дифференциальное и интегрированное исчисление Ньютона, Лейбница было возможно изучать процессы и движение. После этого новые методы успешно внедряются в другие разделы математики, что привело к появлению дифференциальной геометрии, вариационного исчисления и т.п. Третий переворот математики относится к XX веку, хотя его начало и предпосылки связывают с прошлым веком. В начале этого века получили признание неевклидовы геометрии Лобачевского, Римана и Бойяи. Благодаря этому широко распространились новые взгляды на аксиоматическую геометрию и геометрические пространства вообще. Создана теория множеств Кантора, которая стала основой для всей математики. Выявление парадоксальных положений в теории множеств и логики привело к кризису обоснований математики начала XX века. Как правило, в прошлом математику считали наукой об количественных отношениях между величинами. Однако сегодня существует более широкое понимание абстрактных структур Н.Бурбаки, согласно которому математика изучает абстрактное отношение и отношения любого рода. Революция в геометрии XIX века (создание неевклидовых геометрий) также дала новое понимание принципов построения математики на основе аксиоматического метода. Поскольку в процессе работы Лобачевского и других только геометрия основывалась на постулатах, то после создания неевклидовых геометрий стало ясно, что так следует действовать во всех разделах математики. В первую очередь революция в математике касается сферы философии математики, связанной с ее концептуальной структурой и проблемами философского обоснования. А это уже ведет к радикальным переменам в самой математике, которые могут привести к кардинальным изменениям в самой математике. Чтобы подвести итог нашим рассуждениям, охарактеризуйте качественные изменения, связанные с революцией в математике следующими неотъемлемыми чертами: 1. Изменение, углубление смысла (значения) старых понятий. 2. Создаются новые теории и методы математики, которые радикально изменяют прежние представления. 3. Направленное на расширение применения математических понятий и теорий внутри самой математики, а также в ее приложениях. 4. Изменения в основаниях математики и ее философии – это завершение революции, которая произошла в математике. Что бы ни говорил академик Л.Ландау, наука делится на естественные науки (физика и химия), неестественные научные науки; сверхъестественная математика. Но в этом есть доля правды: математику нельзя отнести к естествознанию, но она не является и гуманитарной дисциплиной. Это правда. Это «сверхъестественная» наука, развивающаяся по своим особым законам, поэтому для обсуждения особенностей научных революций в математике нам нужен этот последний параграф. Заключение По мнению авторов концепции, научные революции представляют собой достаточно спорный взгляд на развитие науки. Хотя Кун и не открыл ничего нового, о наличии нормальных периодов развития науки говорили многие авторы. Какие особенности философских взглядов Куна на развитие научного познания? Во-первых, у Куна целостная концепция развития науки, а не просто описание событий из истории науки. С этим подходом она полностью разрывает с целым рядом традиционных философских традиций в области науки. Кроме того, в своей концепции Кун категорически отрицает позитивизм - господствующее течение философии науки с конца XIX века. Куна в противоположность позитивистской позиции рассматривает не готовые структуры научного знания, а раскрытие механизма развития науки, т.е. исследование движения научного знания. В отличие от широко распространенного кумулятивистского взгляда на науку, Кун не считает что наука развивается по пути увеличения знаний. Он считает, что накопление знаний возможно только на стадии нормальной науки. Научная революция по Куну, меняя взгляд на природу не ведет к прогрессам в связи с ростом объективной истинности научных знаний. Но он не рассматривает этот вопрос: является ли новая парадигма лучше старой, с точки зрения прогресса в научном познании? Однако, по мнению Куна, новая парадигма, с его точки зрения, ничем не хуже старой. Я не стал упоминать некоторые интересные рассуждения Куна о учебниках и научных группах, которые непосредственно относятся к теме реферата. Литература [1] Т.Кун. Структура научных революций. М., Прогресс, 1975. [2] Г.И.Рузавин. Об особенностях научных революций в математике // В кн.: Методологический анализ закономерностей развития математики, М., 1989, с. 180-193. [3] Г.И.Рузавин. Диалектика математического познания и революции в его развитии // В кн: Методологический анализ математических теорий, М., 1987, с. 6-22. [4] И.С.Кузнецова. Гносеологические проблемы математического знания. Л., 1984. |
