ОТВЕТЫ. 1. Издержки производства и их виды. Предельные издержки и предельный доход. Отдача от масштаба производства

• Название: 1. Издержки производства и их виды. Предельные издержки и предельный доход. Отдача от масштаба производства
• Анкор: ОТВЕТЫ.docx
• Дата: 22.12.2017
• Размер: 1.23 Mb.
• Имя файла: ОТВЕТЫ.docx
• Тип: Документы; #12550
• страница: 11 из 39

Косвенный метод наименьших квадратов

Препятствие к применению метода наименьших квадратов, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если:

1. 
   привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;
   
2. 
   затем применить метод наименьших квадратов к каждому уравнению в приведенной форме и получить оценки ее параметров;
   
3. 
   перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров.
   

Эта методика получила название косвенного метода наименьших квадратов и позволяет получать состоятельные и несмещенные оценки параметров структурной форму системы одновременных уравнений.
Пример.

Рассмотрим самую простую структурную форму системы одновременных уравнений: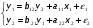
(7.1.10)
Пусть модель реализуется по следующим данным:
7.1.1 Исходные данные

№ п/п	Y1	Y2	X1	X2
1	2	10	150	1
2	3	12	200	2
3	5	15	150	4
4	4	16	140	3
5	6	25	300	5
6	3	16	190	2
7	5	20	250	5
8	8	30	450	9
9	3	11	170	2
В среднем	4,3	17,2	222,2	3,7

Найдем отклонения от средних значений по каждой переменной (табл. 7.1.2):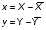

Перейдем от структурной к приведенной форме, для этого выразим из первого уравнения у₂: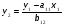
(7.1.11)
7.1.2. Отклонения от средних уровней

№ п/п	y1	y2	x1	x2
1	-2,3	-7,2	-72,2	-2,7
2	-1,3	-5,2	-22,2	-1,7
3	0,7	-2,2	-72,2	0,3
4	-0,3	-1,2	-82,2	-0,7
5	1,7	7,8	77,8	1,3
6	-1,3	-1,2	-32,2	-1,7
7	0,7	2,8	27,8	1,3
8	3,7	12,8	227,8	5,3
9	-1,3	-6,2	-52,2	-1,7

Тогда система одновременных уравнений будет иметь вид: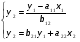
(7.1.12)
Приравняем правые части и выразим у₁: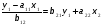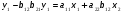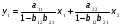
;
;

. (7.1.13)
Получившееся уравнение является первым уравнением системы в приведенной форме.

Аналогичным образом поступим для получения второго уравнения. Из второго уравнения структурной формы выразим y₁: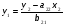

. (7.1.14)
Подставим правую часть тождества в первое структурное уравнение: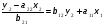

.
Выразим y₂: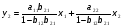

(7.1.15)

Таким образом, мы получили систему приведенных уравнений: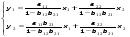
(7.1.16)
Обозначим для удобства восприятия получившиеся нелинейные коэффициенты при независимых переменных как :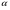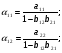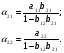


(7.1.17)

Получим систему приведенных уравнений: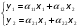

(7.1.18)

Решим систему приведенных уравнений, используя данные табл. 7.1.2, методом наименьших квадратов: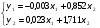



(7.1.19)
Теперь нужно перейти к структурной форме, т.е.: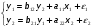

Сопоставив первое уравнение приведенной и структурных форм видим, что для перехода к структурному виду следует переменную х₂ представить как комбинацию переменных у₂ и х₁. Это можно сделать, выразив х₂ из второго уравнения приведенной формы: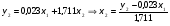
. (7.1.20)
Подставим х₂ в первое уравнение системы приведенной формы: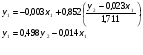
(7.1.21)

Мы получили первое уравнение системы структурной формы.

Теперь выразим переменную х₁ из первого уравнения приведенной формы: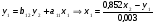
(7.1.22)
и подставим х₁ во втрое уравнение системы приведенной формы: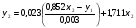

(7.1.23)

Получим, таким образом, второе уравнение системы структурной формы: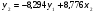
(7.1.24)
Мы получили систему одновременных, структурных уравнений: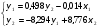
(7.1.25)
Чтобы перейти от отклонений переменных от средних к их значениям (от значений табл. 7.1.2 к табл. 7.1.1), нужно определить свободные члены для каждого из уравнений. Рассчитываются они по формулам: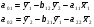
(7.1.26)
Подставим средние значения (табл. 7.1.1) и коэффициенты при переменных в структурной форме: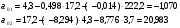
(7.1.27)
Тогда система структурных уравнений примет вид: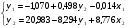
(7.1.28)
Полученные оценки являются состоятельными и несмещенными, в отличие от оценок метода наименьших квадратов, если применить его к каждому уравнению в отдельности, то получим уравнения множественной регрессии: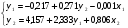
(7.1.29)
Как видно, различия значительны, особенно во втором уравнении, где имеется даже несовпадение знаков коэффициента при у₁.