ОТВЕТЫ. 1. Издержки производства и их виды. Предельные издержки и предельный доход. Отдача от масштаба производства

• Название: 1. Издержки производства и их виды. Предельные издержки и предельный доход. Отдача от масштаба производства
• Анкор: ОТВЕТЫ.docx
• Дата: 22.12.2017
• Размер: 1.23 Mb.
• Имя файла: ОТВЕТЫ.docx
• Тип: Документы; #12550
• страница: 12 из 39

Проблема идентификации

В рассмотренном примере (7.1.10) уравнения были однозначно разрешимы относительно исходных параметров, что позволило найти их состоятельные оценки.

Такая ситуация не всегда имеет место. Возникает проблема идентификации, то есть однозначности определения параметров структурной модели от приведенной формы. Переход необходим, поскольку экономический смысл и интерпретацию имеют только параметры структурной формы.
Структурный параметр называется идентифицируемым, если он может быть однозначно определен с помощью метода наименьших квадратов. Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры.

Модель 7.1.10 – точно идентифицируемая, при переходе от приведенной к структурной форме мы получили единственно возможные оценки.
Структурный параметр называется неидентифицируемым, если его значение невозможно получить, даже зная точные значения параметров приведенной формы.

Полная форма структурной модели (7.1.5), где присутствуют все переменные, всегда неидентифицируема.
Структурный параметр называется сверхидентифицируемым, если косвенный метод наименьших квадратов дает несколько различных его оценок.

Модель: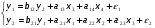
(7.1.30)

будет сверхидентифицируемой, поскольку из восьми коэффициентов приведенной формы нельзя однозначно определить семь – структурной формы.

Сверхидентифицируемая система в отличие от неидентифицируемой практически решаема, но не косвенным методом наименьших квадратов, а специальными методами.

Для проверки структурной модели на идентификацию, нужно проверить каждое уравнение системы:

1. 
   модель считается идентифицируемой, если каждое уравнение системы идентифицируемо;
   
2. 
   если хотя бы одно уравнение неидентифицируемо, то вся модель считается неидентифицируемой;
   
3. 
   если в модели нет неидентифицируемых уравнений, но присутствует хотя бы одно сверхидентифицируемое, то модель – сверидентифицируемая.
   

Условия идентифицируемости проверяются для каждого уравнения в отдельности. Чтобы уравнение было идентифицируемым, нужно, чтобы:
1+n_x=n_y,

где n_x – число экзогенных переменных, содержащихся в системе, но отсутствующих в данном уравнении системы;

n_y – число эндогенных переменных в данном уравнении.

Если 1+n_xy, уравнение неидентифицируемо;
1+n_x>n_y, то уравнение сверхидентифицируемо.
Пример 1.

Проверим систему: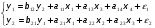
(7.1.31)
на идентификацию.

В первом уравнении системы отсутствует только одну экзогенную переменную х₂, тогда:

n_x=1, n_y=2 и 1+n_x= 2 = n_y=2, то есть первое уравнение идентифицируемо;

Во втором нет переменной х₄:

n_x=1, n_y=2 и 1+n_x= 2 = n_y=2, второе уравнение также идентифицируемо,

а, следовательно, модель идентифицируема и может быть решена косвенным методом наименьших квадратов.
Пример 2.

Если в нашем примере коэффициент при х₁ во втором уравнении будет равен нулю: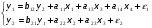
(7.1.32)
Тогда в втором уравнении отсутствуют две экзогенные переменные: х₁, х₄,:

n_x=2, n_y=2 и 1+n_x= 3 > n_y=2, второе уравнение сверхидентифицируемо;

Следовательно, система в целом сверхидентифицируема.
Пример 3.

Система: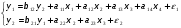
(7.1.33)
будет неидентифицируемой, поскольку в первом уравнении присутствуют все переменные системы:

n_x=0, n_y=2 и 1+n_x= 1 < n_y=2.

Ранговое условие идентифицируемости (достаточное):

Для разрешимости системы структурных уравнений достаточно, чтобы ранг матрицы, составленной из коэффициентов эндогенных и экзогенных переменных, отсутствующих в данном уравнении, но присутствующих в других уравнениях системы, был не меньше, чем число эндогенных переменных в системе без одного, а определитель этой же матрицы не был равен нулю.

Пример.

Имеется система структурных уравнений: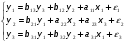
(7.1.34)
Проверим ее на идентификацию

Первое уравнение. Необходимое (счетное) условие: n_x=2 (отсутствуют х₂, х₃), n_y=3, 1+n_x=n_y – уравнение идентифицируемо.

Составим матрицу коэффициентов при отсутствующих переменных (y₃ и х₃):

Уравнение	х2	х3
2	а22	а23
3	0	0

Определитель матрицы коэффициентов равен нулю, ранг матрицы равен единице, он меньше числа экзогенных переменных в системе без одного (3-1=2). Достаточное условие не выполняется, уравнение нельзя признать идентифицируемым по ранговому правилу.

Для второго уравнения выполняются необходимое и достаточное условия идентификации.

Счетное правило: n_x=1 (отсутствует х₁), n_y=2, 1+n_x=n_y – уравнение идентифицируемо.

Матрица коэффициентов:

Уравнение	у3	х1
1	b13	а11
3	1	а31

Определитель матрицы не равен нулю. Ранг матрицы равен двум, он равен числу экзогенных переменных в системе без одного (3-1=2). Итак, второе уравнение системы точно идентифицируемо.

Для третьего уравнения выполняется необходимое условие:

n_x=2 (отсутствуют х₂ и х₃), n_y=3, 1+n_x= n_y.
Матрица коэффициентов:

Уравнение	х2	х3
1	0	0
2	а22	а23

Определитель матрицы равен нулю. Ранг матрицы равен единице, он меньше числа экзогенных переменных в системе без одного (3-1=2). Итак, третье уравнение системы неидентифицируемо по ранговому правилу.

Наша система идентифицируема по счетному правилу (необходимое условие идентификации), но ее нельзя признать идентифицируемой по достаточному условию (ранговое правило не выполняется для первого и третьего уравнений системы).

Оценить параметры можно только для идентифицируемых и сверхидентифицируемых систем. Для однозначно идентифицируемых систем применяется косвенный метод наименьших квадратов. Найти параметры сверхидентифицируемой системы позволяет двухшаговый метод наименьших квадратов.

Использование систем одновременных эконометрические уравнений позволяет строить более реалистичные модели, поскольку отражают взаимосвязи между экономическими переменными. Одна и та же экономическая переменная может рассматриваться и как факторная и как результативная. Использование систем совместных уравнений позволяет решать проблемы, связанные с мультиколлинеарностью факторов в уравнениях множественной регрессии.

При оценке параметров системы одновременных уравнений исследователь сталкивается с проблемой идентификации. Точно идентифицируемые системы могут оцениваться косвенным методом наименьших квадратов.

Наиболее широко системы эконометрических уравнений используются для построения макроэкономических моделей функционирования той или иной страны. Большинство из них представляют собой мультипликаторные модели кейнсианского типа с той ил иной мерой сложности. 

Пример: статистическая модель Кейнса для описания народного хозяйства  страны в простом варианте имеет следующий вид: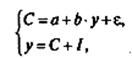



где С – личное потребление в постоянных ценах,

       у – национальный доход в постоянных ценах;

       I – инвестиции;

      - случайная величина
25. Эконометрическое моделирование основной тенденции развития временного ряда. взаимосвязей на основе данных временных рядов.