Физика 1 - 3 задание. 1. Какая из приведенных ниже формул выражает понятие скорости

• Название: 1. Какая из приведенных ниже формул выражает понятие скорости
• Дата: 17.12.2018
• Размер: 1.05 Mb.
• Имя файла: Физика 1 - 3 задание.doc
• Тип: Документы; #60610
• страница: 3 из 3

м/с;
200. Момент импульса вращающегося тела относительно оси определяется выражением:

А) ;

201. Укажите выражение, определяющее момент импульса материальной точки относительно некоторой неподвижной точки:

А) ;

202. Частица массы m движется равномерно вдоль оси X. Как направлен вектор момента импульса 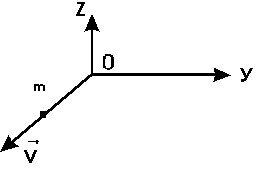частицы относительно точки О:



А) Никуда, ;

203. Какая из приведенных формул выражает основной закон динамики вращательного движения:

А) ;

204. Какая из приведенных формул выражает момент импульса тела при вращательном движении:

А) ;

205. К диску приложена одна из четырех сил. Под действием какой силы диск будет вращаться с большим угловым ускорением:



А) Моменты всех сил сообщают одинаковое угловое ускорение;

206. К диску приложена одна из четырех сил. Под действием какой силы диск будет вращаться с наименьшим угловым ускорением:



А) Моменты всех сил сообщают одинаковое угловое ускорение;

207. К диску радиусом R приложены две одинаковые по величине силы 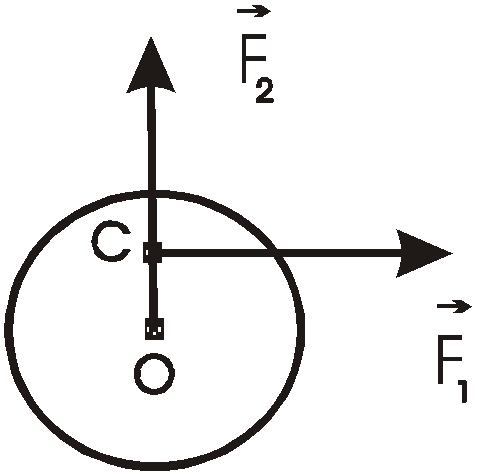. Чему равен результирующий момент сил относительно оси О, перпендикулярной плоскости диска (ОС= R/2):



А) FR/2;

208. Тонкий однородный стержень длиной и массой m=0,4 кг вращается с угловым ускорением =3 рад/с около оси, проходящей перпендикулярно стержню через его середину. Чему равен вращающий момент:

А) 0,025 ;

209. К ободу однородного диска радиусом R приложена постоянная касательная сила F. При вращении на диск действует момент сил трения .Найти массу диска, если он вращается с постоянным угловым ускорением :

А) ;

210. К ободу колеса массой m=50 кг, имеющего форму диска радиусом R=0,5 м, приложена касательная сила F=100 Н. Чему равно угловое ускорение колеса:

А) 8 рад/с;

211. Укажите формулу для кинетической энергии тела, вращающегося вокруг закрепленной оси:

А) ;

212. По какой формуле можно рассчитать работу при вращательном движении твердого тела:

А) ;

213. Какую работу надо совершить, чтобы остановить маховик, вращающийся с угловой скоростью : Момент инерции маховика относительно оси вращения равен :

В) ;

214. Платформа в виде диска радиусом R вращается по инерции с угловой скоростью . На краю платформы стоит человек, масса которого равна m. С какой угловой скоростью будет вращаться платформа, если человек перейдет в ее центр: Момент инерции платформы J. Момент инерции человека рассчитывать как для материальной точки:

А) ;

215. Маховик, момент инерции которого I=63,6кгм², вращается с угловой скоростью . Найти момент сил торможения М, под действием которого маховик останавливается через время t=20c.

A) 100Hм;

216. Маховик вращается по закону, выражаемому уравнением = А+ Вt+ Ct², где А=2рад, В=16рад/с, С=-2рад/с². Момент инерции I колеса равен 50кгм². Найти вращающий момент М:

А) 200Нм;

217. Момент инерции однородного стержня относительно оси, проходящей перпендикулярно стержню на расстоянии l/6 от ее центра, равен кml², где к равно:

С) 1/9;

218. Момент инерции однородного стержня относительно оси, проходящей перпендикулярно стержню на расстоянии l/4 от ее центра, равен кml², где к равно:

D) 3/4;

219. Момент инерции однородного диска относительно оси, проходящей перпендикулярно диску на расстоянии R/2 от центра диска, равен кmR², где к равно:

А) 3/4;

220. Момент инерции однородного диска относительно оси, проходящей перпендикулярно диску через обод диска равен кmR², где к равно:

А) 3/2;

221. Момент инерции однородного диска относительно оси, проходящей перпендикулярно диску на расстоянии R/3 от центра диска, равен кmR², где к равно:

А) 11/18;

222. Момент силы определяется формулой:

D) ;

223. Момент импульса материальной точки, вращающейся по окружности:

А) ;

224. Угловая скорость вращающегося тела равна ω, момент инерции I. Через какой промежуток времени тело остановится, если к нему приложить тормозящий момент силы М:

A) I ω/М;

225.Однородный цилиндр R=10 см, массой 4 кг вращается с угловой скоростью 10 рад/с вокруг оси симметрии. При действии, какого тормозящего момента он остановится через 5 с:

А) 40 мН^.м;

226. Вал вращается с угловой скоростью ω =10 рад/с. Определить момент силы, создаваемый валом, если к нему приложена мощность 400 Вт.

А) 40 Н^.м;

227. Однородный диск массой 5 кг и радиусом 20 см вращается с угловым ускорением 3 рад/с². Определить момент силы, приложенный к диску.

А) 0,3 Н^.м;

228. Теорема Штейнера имеет вид:

А) .

229. На однородный цилиндр радиусом 10 см массой 2 кг, способный вращаться вокруг оси симметрии, намотан тонкий шнур. С какой силой надо дернуть шнур, чтобы придать цилиндру угловое ускорение 5 рад/с²: (Н)

А) 0,5;

230. Как изменится момент импульса свободно вращающегося тела при уменшении момента инерции в два раза:

D) не изменится;
231. Какое из соотношений выражает внутреннее трение между двумя слоями газа (жидкость):

А) F=;

232. Давление водного столба в озере на глубине 50 м составит, (атмосферное давление не учитывается):

А) 490 кПа;

233. 10 мм рт. столба составляет (Па):

А) 1333;

234. Плотность льда составляет 0,9 г/см³. Какая часть его объема видна над поверхностью воды (в %):

D) 9;

235. В широкой части горизонтальной трубы скорость воды составляет 0,20 м/с. Определить ее скорость в узкой части трубы, диаметр которой в 1,5 раза меньше:

В) 0,30 м/с;

236. Бак высотой 0,9 м до краев заполнен водой. В полуметре от днища пробили небольшое отверстие. Образовавшаяся струя воды имеет скорость (м/с):

С) 2,0;

237. По гладкой круглой трубе диаметром 5 см течет вода (η=1 мПа^.с) со средней скоростью 10 см/с. Число Рейнольдса для этого случая составит:

А) 5000;

238. По трубе течет машинное масло (η_дин=0,1 Па^.с, ρ=0,8 г/см³). Предельная скорость ламинарного течения масла равна 3,2 см/с. При какой скорости течения глицерина (η_дин=1,5 Па^.с, ρ=1,26 г/см³ ) в той же трубе течение перейдет в турбулентное (примерно, м/с):

D) 0,14;

239. Какое из выражений является уравнением непрерывности при тичении несжимаемой жидкости в трубе:

А) Sconst;

240. Жидкость течет по трубе с переменным сечением без трения. В каком сечении трубы давление в жидкости максимально: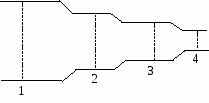



D) 4;

241. Во сколько раз отличаются диаметры горизонтальной трубы в ее узкой и широкой части, если скорости течений воды в этих частях равны соответственно 20 см/с и 45 см/с:

D) 2,25;