|
Ответы к коллоквиуму по физике. 1 Какие процессы называются колебательными Гармонические колебания. Уравнение и график гармонических колебании. Частота колебаний. Укажите на графике амплитуду, период колебания, начальную фазу
№ 52 Физические поля организма человека: спектр теплового излучения организма. Поток теплового излучения в ИК и радио диапазонах. Использование теплового излучения организма для диагностики заболеваний.
Тепловое излучение свойственно всем телам при абсолютной температуре Т > 0, и его источником является внутренняя энергия хаотического теплового движения их атомов и молекул.
Инфракрасное (ИК) излучение (частота 1014 Гц, длина волны 3-10 мкм);
Наиболее яркую информацию о распределении температуры поверхности тела человека и ее изменениях во времени дает метод динамического инфракрасного тепловидения.
Тепловизоры регистрируют тепловое излучение. С поверхности тела весь диапазон разбивается на мелкие интервалы, каждому присваивается свой цвет.
Тепловидение в биологии и в медицине:
Инфракрасное тепловидение тела человека дает информацию о температуре верхних слоев кожи – рогового слоя эпидермиса. Наиболее распространенным применением ИК – тепловидения в медицине является визуализация кровоснабжения нижных конечностей. Если кровоснабжение в них нарушено, то температура дистальных участков резко снижена.
Регистрируя размер областей со сниженной температурой можно определить степень выраженности заболевания, а так же эффективность терапевтических мероприятий.
|
№ 53 Моделирование как метод познания. Виды моделей. Адекватность, границы применимости моделей. Приведите примеры использования моделей при изучении биологических систем. Моделирование роста биологической популяции при различных условиях функционирования системы.
Моделирование — это метод, при котором производится замена изучения некоторого сложного объекта (процесса, явления) исследованием его модели. Основные этапы моделирования можно свести к следующим:
1) Первичный сбор информации. 2) Постановка задачи. 3) Обоснование основных допущений. 4) Создание модели, ее исследование. 5) Проверка адекватности модели реальному объекту.
Модели могут применяться в случаях: 1) невозможность изучения реального объекта 2) излучаемый процесс сопровождается другими, не являющимися предметами изучения в условиях данной задачи. Виды моделей:
Физическая модель имеет физическую природу, часто ту же, что и исследуемый объект. Например, течение крови по сосудам моделируется движением жидкости по сосудам.
Биологические модели представляют собой биологические объекты, удобные для экспериментальных исследований, на которых изучаются свойства, закономерности биофизических процессов в реальных сложных объектах. Например, закономерности возникновения и распространения потенциала действия в нервных волокнах были изучены только после нахождения такой удачной биологической модели, как гигантский аксон кальмара. Математические модели — описание процессов в реальном объекте с помощью математических уравнений, как правило, дифференциальных. Для реализации математических моделей в настоящее время широко используются компьютеры.
Если процессы в модели имеют другую физическую природу, чем оригинал, но описываются таким же математическим аппаратом (как правило, одинаковыми дифференциальными уравнениями), то такая модель называется аналоговой. Обычно в виде аналоговой модели используются электрические. Например, аналоговой моделью сосудистой системы является электрическая цепь из сопротивлений, емкостей и индуктивностей.
Основные требования, которым должна отвечать модель.
1. Адекватность - модель должна с заданной степенью точности воспроизводить закономерности изучаемых явлений.
2. Должны быть установлены границы применимости модели, то есть четко заданы условия, при которых выбранная модель адекватна изучаемому объекту, поскольку ни одна модель не дает исчерпывающего описания объекта.
|
№ 54 Модель “хищник - жертва”. Фазовый портрет системы. Применение этой модели в медицине.
1)Имеется популяции, состоящие из 2х типов особей: х – число жертв, у – число хищников
2) Хищники питаются только жертвами, учитываются процессы естественной гибели и роста 2х типов особей.
где γ скорость размножения жертв; δ - скорость естественной гибели жертв; Альфа — скорость гибели жертв в результате встреч с хищниками, пропорциональная числу встреч, а значит, произведению ху.
г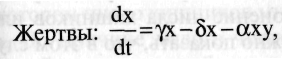 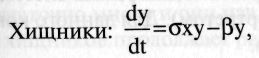 де σху — скорость размножения хищников, пропорциональная числу встреч с жертвами; (Беттау — скорость естественной гибели хищников. Тогда после простых преобразований получим: Это сложная система нелинейных дифференциальных уравнений, которую в общем виде аналитически решить нельзя. Выясним сначала, есть ли в такой системе стационарное состояние, когда x=const и y=const, т.е. де σху — скорость размножения хищников, пропорциональная числу встреч с жертвами; (Беттау — скорость естественной гибели хищников. Тогда после простых преобразований получим: Это сложная система нелинейных дифференциальных уравнений, которую в общем виде аналитически решить нельзя. Выясним сначала, есть ли в такой системе стационарное состояние, когда x=const и y=const, т.е. 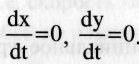 Система дифференциальных уравнений при этом сводится к алгебраическим: Система дифференциальных уравнений при этом сводится к алгебраическим:
Р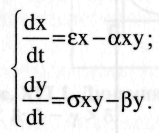 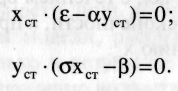 ешения этой системы таковы: ешения этой системы таковы: 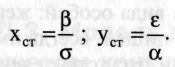
Вывод: стационарное состояние существует и численность особей хищников и жертв определяется коэффициентом встреч, размножения и гибели. Если вдруг по каким-то причинам произошло отклонение численности хищников или жертв от стационарного состояния, то в системе возникают колебания числа хищников и жертв относительно стационарного значения. Фазовая диаграмма системы зависимость числа у от числа жертв 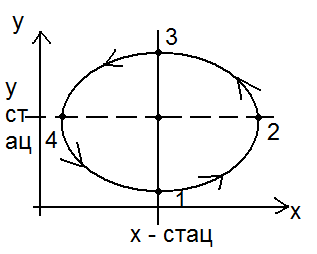 1 – 2: по причине малого числа хищников, жертвы размножаются => улучшаются условия питания для хищников и они тоже размножаются. 2 – 3: по причине большого числа хищников скорость поедания жертв возрастает, а число жертв однако оно еще достаточно велико и число хищников продолжает расти. 3 – 4: Число жертв достигает стационарного значения и продолжает убывать, следовательно условия питания хищников ухудшается и их число падает. Модель «хищник – жертва» используется в настоящее время в медицине, так при моделировании онкологических заболеваний опухолевые клетки рассматриваются как жертвы, а лимфоциты, которые могут их подавлять, как хищники 1 – 2: по причине малого числа хищников, жертвы размножаются => улучшаются условия питания для хищников и они тоже размножаются. 2 – 3: по причине большого числа хищников скорость поедания жертв возрастает, а число жертв однако оно еще достаточно велико и число хищников продолжает расти. 3 – 4: Число жертв достигает стационарного значения и продолжает убывать, следовательно условия питания хищников ухудшается и их число падает. Модель «хищник – жертва» используется в настоящее время в медицине, так при моделировании онкологических заболеваний опухолевые клетки рассматриваются как жертвы, а лимфоциты, которые могут их подавлять, как хищники
|
|
|
№ 55 Фармакокинетическая модель изменения концентрации лекарственного препарата при различных способах его введения в организм: инъекция, инфузия, сочетание инъекции и инфузии.
Для описания кинетики изменения концентрации введенного в организм лекарственного препарата предлагается так называемая фармакокинетическая модель.
ОсновныеДопущения: 1. Не будем рассматривать систему органов, через которые последовательно проходит лекарство. Исключим многостадийность процессов ввода, переноса, вывода лекарственного вещества.
2. Не будем учитывать молекулярные механизмы процессов (например, проницаемость вещества, химические превращения).
3. Процессы ввода и вывода сведем к скорости.
Рассмотрим законы изменения c(t) при различных способах введения лекарства
. 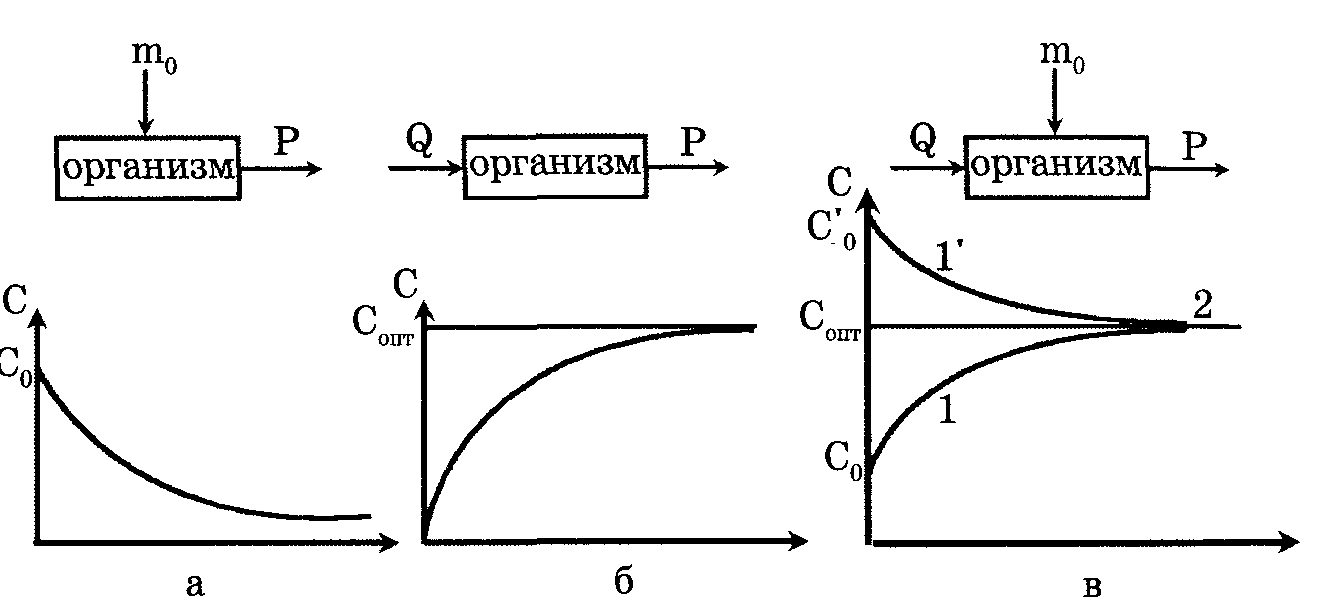
1-й способ. Инъекция (рис.а). Представим себе организм как систему объемом V, после введения в которую лекарственного препарата массой m0, начинается его удаление из организма. Распределение препарата по объему предполагается равномерным. Скорость удаления р препарата из организма прямо пропорциональна его массе в организме: р = - km, k - коэффициент удаления препарата из организма. Скорость изменения массы лекарственного вещества в организме dm/dt=р: и следовательно dm/dt=-km. Решение этого дифференциального уравнения, с учетом начального условия, что при t = 0 масса введенного лекарственного m = m0, m = m0*e^-kt. Концентрация лекарственного препарата в организме (например, в крови), с = m/V c=m0/V*e^-kt или с = c0 • е^-kt, где V - объем крови, c0 - начальная концентрация.
Концентрация лекарственного препарата в крови будет непрерывно снижаться по убывающему экспоненциальному закону.
2-й способ. Инфузия (рис. б). В этом случае изменение массы лекарственного препарата в организме dm/dt определяется не только скоростью его удаления р, но и скоростью введения Q - количеством лекарственного вещества, вводимого в организм за единицу времени: dm/dt=Q-km
Решим это дифференциальное уравнение с учетом, что при t = 0 масса m= 0: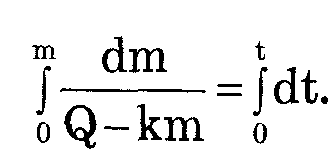 Введем новую переменную U=Q-km, dU=-kdm, dm=-dU/k, Введем новую переменную U=Q-km, dU=-kdm, dm=-dU/k,
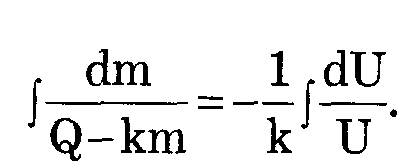 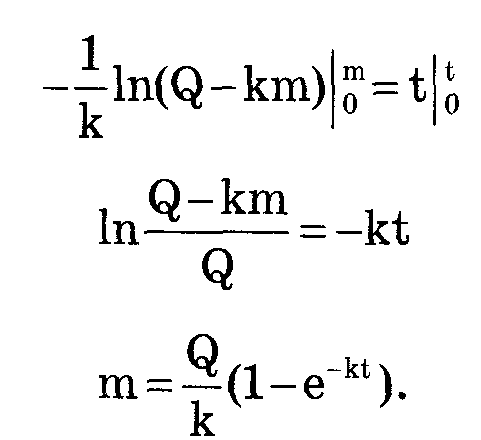 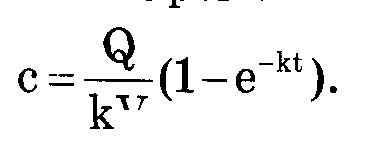 В начальный момент времени, при t = 0, с = 0. При t—>°° величина е^-kt->0 и с —>Q/kVЧерез некоторое время после начала введения лекарства устанавливается постоянная концентрация c=Q/kV В начальный момент времени, при t = 0, с = 0. При t—>°° величина е^-kt->0 и с —>Q/kVЧерез некоторое время после начала введения лекарства устанавливается постоянная концентрация c=Q/kV
3-й способ. При этом фармакокинетическая модель примет вид: C=Q/KV-1/V (Q/k-m0)*e^-kt
|
№ 56 Организм как открытая термодинамическая система. Уравнение Пригожина. Стационарное состояние термодинамической системы.
Любая живая система открыта – в ней происходит непрерывный обмен между окружающей средой и системой веществом и энергией.
Особенностью биосистемы является то, что они не просто открытые системы, а системы находящиеся в стационарном состоянии.
При стационарном состоянии приток и отток энтропии происходит с постоянной скорость, поэтому общая энтропия не меняется во времени.
Равновесное Стационарное
Сходства:
Все параметры системы (t, p, v, s) остаются неизменными во времени.
Различия:
E своб => min E своб = const
S - max S max > S S – const
1) Естественные состояния 1)Постоянство параметров
Системы не требуется требуется поддерживать за
Поддерживать счет процессов обмена с ок.ср
2) нет градиентов 2) есть градиент
3) нет потоков 3) есть поток
Для открытой системы справедливо уравнение ПРИГОЖИНА:

Для стац.сост.ур-ние Пригожина выглядит так:
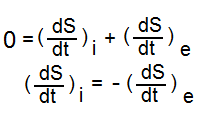
|
|
| |
|
|
 Скачать 5.18 Mb.
Скачать 5.18 Mb.