Ответы по железобетонным конструкциям. 1. Какие требования предъявляют к трещиностойкости железобетонной конструкции и как они делятся по категориям Охарактеризуйте категории трещиностойкости

• Название: 1. Какие требования предъявляют к трещиностойкости железобетонной конструкции и как они делятся по категориям Охарактеризуйте категории трещиностойкости
• Анкор: Ответы по железобетонным конструкциям.doc
• Дата: 03.02.2017
• Размер: 2.43 Mb.
• Имя файла: Ответы по железобетонным конструкциям.doc
• Тип: Документы; #1893
• страница: 1 из 4

1. Какие требования предъявляют к трещиностойкости железобетонной конструкции и как они делятся по категориям? Охарактеризуйте категории трещиностойкости.


СНиП ЖБК п. 1.16

Расчет по предельным состояниям второй группы должен обеспечивать конструкции от:

- образования трещин, а также их чрезмерного или продолжительного раскрытия (если по условиям эксплуатации образование или продолжительное раскрытие трещин недопустимо);

К трещиностойкости конструкций (или их частей) предъявляются требования соответствую­щих категорий в зависимости от условий, в кото­рых они работают, и от вида применяемой арматуры:

а) 1-я категория — не допускается образование трещин (конструкции, воспринимающие давление жидкости и газа, если все сечение растянуто, арматура преднапряжена);

б) 2-я категория — допускается ограниченное по ширине непродолжительное раскрытие трещин a_crc1 при условии обеспечения их последующего надежного закрытия (зажатия) (конструкции, эксплуатируемые на открытом воздухе, в грунте ниже уровня грунтовых вод);

в) 3-я категория — допускается ограниченное по ширине непродолжительное a_crc1 и продолжитель­ное a_crc2 раскрытие трещин (конструкции, эксплуатируемые в закрытом помещении и другие при определенных видах арматуры).

Под непродолжительным раскрытием трещин по­нимается их раскрытие при совместном действии постоянных, длительных и кратковременных нагру­зок, а под продолжительным - только постоянных и длительных нагрузок.

Для второй группы предельных состояний нагрузки принимаются с коэффициентом γf=1,0 (за исключением конструкций 1 категории трещиностойкости).

2. В чем состоит цель расчета по образованию и раскрытию трещин?
СНиП ЖБК п. 4.хх, 5.хх

Сущность расчета по раскрытию трещин, нормальных и наклонных к продольной оси заключается в определении ширины раскрытия трещин на уровне растянутой арматуры a_crc и сравнение ее с предельно допустимой шириной раскрытия трещин.

Расчет по образованию трещин центрально-растянутых элементов заключается в проверке условия, что трещины в сечениях, нормальных к продольной оси, не образуются, если продольная сила N от действия внешней нагрузки не превосходит внутреннего предельного усилия в сечении перед образованием трещин Ncrc, т.е. N<=Ncrc.

Расчет по образованию трещин изгибаемых, внецентренно-сжатых и внецентренно растянутых элементов заключается в проверке условия, что трещины в сечениях, нормальных к продольной оси элемента, не образуются если момент внешних сил M не превосходит момента внутренних усилий в сечении перед образованием трещин Mcrc.

3. Каковы основные предпосылки, принимаемые в расчете по образованию трещин? Как фор­мулируется исходные положения расчета по образованию трещин при центральном растя­жении, при изгибе
СНиП ЖБК

4.2. Для изгибаемых, растянутых и внецентренно сжатых железобетонных элементов усилия, воспри­нимаемые нормальными к продольной оси сечения­ми при образовании трещин, определяются исходя из следующих положений:

• 
  сечения после деформации остаются плоскими;
  
• 
  наибольшее относительное удлинение крайнего растянутого волокна бетона равно 2 R_bt,ser/E_b;
  
• 
  напряжения в бетоне сжатой зоны (если она име­ется) определяются с учетом упругих или неупру­гих деформаций бетона, при этом наличие неупругих деформаций учитывается уменьшением ядро­вого расстояния r (см. п. 4.5);
  
• 
  напряжения в бетоне растянутой зоны распределены равномерно и равны по величине R_bt,ser;
  
• 
  напряжения в ненапрягаемой арматуре равны ал­гебраической сумме напряжений, отвечающих приращению деформаций окружающего бетона, и нап­ряжений, вызванных усадкой и ползучестью бетона;
  
• 
  напряжения в напрягаемой арматуре равны ал­гебраической сумме ее предварительного напряже­ния (с учетом всех потерь) и напряжения, отвечаю­щего приращению деформаций окружающего бетона.
  

4. Расчет трещинообразования центрально растянутых элементов. Чему равно внутреннее усилие перед образованием трещин центрально-растянутого элемента?
СНиП ЖБК 4.хх – если ничего не знаешь, пишешь отсюда.

Лекция.

Расчет по образованию трещин центрально растянутого элементов сводится к проверке условия:

- в элементах без преднапряжения

N≤N_crc=R_bt,ser*A_b+σ_sA_s=R_bt,ser(A_b+2αA_s)

σ_s=ε_sE_s = ε_btuE_s=(R_bt,ser*E_s/(V_tE_b)=2α R_bt,ser

ε_btu – предельная растяжимость бетона; ε_btu=Rbt/E’bt (модуль упругопластичности бетона)= Rbt/Et*vt (коэффициент упругопластических деформаций)

- в преднапряженных элементах

N≤N_crc=R_bt,ser*A_b+σ_sA_s=R_bt,ser(A_b+2α(A_s+ A_sp)+Р

Где Р – усилие предварительного обжатия, определяемого для стадии эксплуатации с учетом всех потерь

Р= σ_sрA_sр-σ_sA_s

Внутреннее усилие перед образованием трещин центрально растянутого элемента равно N=N_crc


5. Выведите формулы для расчета по образованию трещин изгибаемого элемента.

Расчет по образованию трещин изгибаемых элементов по методу ядровых точек сводится к проверке условия

M≤M_crc

М – момент внешних сил относительно оси, нормальной к плоскости изгиба и проходящей через ядровую точку наиболее удаленную от зоны, трещиностойкость, которой проверяем.

В преднапряженных изгибаемых элементах образованию трещин препятствует сила обжатия, создавая в нижней зоне сжимающее напряжение σ_bp (эпюра напряжений обжатия – трапеция с большим основанием у преднапряженной арматуры).

σ_bp=P/A_red+P*e_0p/W_red

где W_red – упругий момент сопротивления сечения

W_red=I_red/y₀

I_red – момент инерции приведенного сечения относительно оси, проходящей через центр его тяжести.

y₀ – расстояние от центра тяжести сечения до грани, трещиностойкость которой определяется.

A_red – приведенная площадь поперечного сечения

e_0p – расстояние от равнодействующей усилий в продольной арматуре до центра тяжести сечения.

Изгибающий момент М_crc можно представить состоящим из 2 слагаемых – момента М₁, уменьшающего напряжения обжатия крайнего волокна бетона от σ_bp до 0 и момента М₂, вызывающего повышение напряжения в том же сечении от 0 до R_bt,ser.

М₁ = W_red * σ_bp = W_red *(P/A_red+Pe_0p/W_red)=P(W_red/A_red+e_0p)=P(r+e_0p)

r= W_red/A_red – расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от зоны, трещиностойкость которой проверяем.

При определении М₂ принимаем эпюру нормальных напряжений в сжатой зоне элемента треугольной, а в растянутой прямоугольной с напряжением равным R_bt,ser

M₂ = W_p1*R_bt,ser

Где W_p1 – упруго пластический момент сопротивления железобетонного сечения растянутой зоны W_p1=W_red*φ, где φ – коэффициент, учитывающий влияние неупругих деформаций бетона в растянутой зоны.

Выразим Р*( r+e_0p)=M_rp получим

M≤M_crc=M₁+M₂=W_p1R_bt,ser+M_rp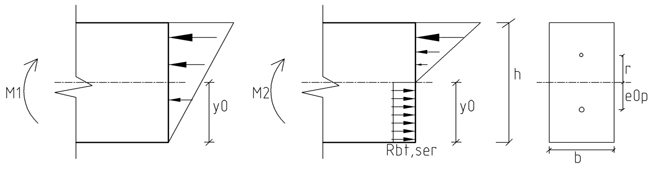


6. Каковы основные положения расчета момента образования трещин при упругой работе бе­тона сжатой зоны элементов? Каковы основные положения расчета момента образования трещин при неупругой работе бетона сжатой зоны элементов?

СНиП п. 4.5 про упругую, п. 4.7. про неупругую – можно списать оттуда.
Перед образованием трещин при двузначной эпюре напряжений в сечениях изгибаемых, внецентренно сжатых, внецентренно растянутых элементов характерно одно и то же напряженно-деформированное состояние – стадия 1.

В расчетах будем исходить из следующих положений: 1) сечения при изгибе остаются плоскими; 2) в бетоне растянутой зоны развиваются неупругие деформации и коэффициент, эпюра нормальных напряжений прямоугольная; 3) в бетоне сжатой зоны деформации только упругие и коэффициент, эпюра нормальных напряжений треугольная.
Бетон сжатой зоны работает упруго, если уровень напряжений k=σ_b/R_b,ser<0,7.

Предельное значение k зависит от вида бетона, эксцентриситета продольной сжимающей силы, длительности действия нагрузки и некоторых других факторов.

Момент внутренних усилий определяется по формуле

M­­_crc= R_bt,serW_pl±M_rp

Где W_pl – упругопластический момент сопротивления предварительно напряженного сечения в растянутой зоне

здесь М_rp — момент усилия Р относительно той же оси, что и для определения М_r; знак момента определяется направлением вращения („плюс" — когда направле­ния вращения моментов M_rpи М_r противоположны; „минус" — когда направления совпадают).

Усилие Р рассматривают:

для предварительно напряженных элементов — как внешнюю сжимающую силу;

для элементов, выполняемых без предваритель­ного напряжения, — как внешнюю растягивающую силу, определяемую по формуле (8), принимая на­пряжения _s и ’_s в ненапрягаемой арматуре численно равными значениям потерь от усадки бетона по поз. 8 табл. 5 (как для арматуры, натягиваемой на упоры).

В некоторых предварительно напряженных элементах перед образованием трезин вследствие высокого уровня напряжений в бетоне сжатой зоны развиваются деформации нелинейной ползучести. Поскольку сечения остаются плоскими, возникают связи, препятствующие свободному развитию неравномерных по высоте сечения неупругих деформаций, стесненная ползучесть сопровождается релаксацией напряжений, эпюра нормальных напряжений искривляется. Момент трещинообразования снижается. Принимают условеи что бетон сжатой зоны работает неупруго если напряжеия вычисленные при треугольной эпюре составляют σ_b/R_b,ser>0,7. В этом случае криволинейную эпюру нормальных напряжений заменяют прямоугольной эпюрой напряжений в обеих зонах сечения, в которых коэффициент упругопластических деформаций:

Vt=vbt=0,5.
M­­_crc= R_bt,serW_pl±M_rp

Внимание. Формулы есть в СНипе п.4.7

W_pl=S_b0+ 2(I_bo+αI_s0+αI’_s0)/(h-x)

S’_b0+αS’_s0-αS₀=(h-x)A_bt/2

7. Каковы основные положения расчета момента образования трещин по способу ядровых моментов?
Расчет по образованию трещин изгибаемых элементов по методу ядровых точек сводится к проверке условия

M≤M_crc

М – момент внешних сил относительно оси, нормальной к плоскости изгиба и проходящей через ядровую точку наиболее удаленную от зоны, трещиностойкость, которой проверяем.

В преднапряженных изгибаемых элементах образованию трещин препятствует сила обжатия, создавая в нижней зоне сжимающее напряжение σ_bp (эпюра напряжений обжатия – трапеция с большим основанием у преднапряженной арматуры).

σ_bp=P/A_red+P*e_0p/W_red

где W_red – упругий момент сопротивления сечения

W_red=I_red/y₀

I_red – момент инерции приведенного сечения относительно оси, проходящей через центр его тяжести.

y₀ – расстояние от центра тяжести сечения до грани, трещиностойкость которой определяется.

A_red – приведенная площадь поперечного сечения

e_0p – расстояние от равнодействующей усилий в продольной арматуре до центра тяжести сечения.

Изгибающий момент М_crc можно представить состоящим из 2 слагаемых – момента М₁, уменьшающего напряжения обжатия крайнего волокна бетона от σ_bp до 0 и момента М₂, вызывающего повышение напряжения в том же сечении от 0 до R_bt,ser.

М₁ = W_red * σ_bp = W_red *(P/A_red+Pe_0p/W_red)=P(W_red/A_red+e_0p)=P(r+e_0p)

r= W_red/A_red – расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от зоны, трещиностойкость которой проверяем.

При определении М₂ принимаем эпюру нормальных напряжений в сжатой зоне элемента треугольной, а в растянутой прямоугольной с напряжением равным R_bt,ser

M₂ = W_p1*R_bt,ser

Где W_p1 – упруго пластический момент сопротивления железобетонного сечения растянутой зоны W_p1=W_red*φ, где φ – коэффициент, учитывающий влияние неупругих деформаций бетона в растянутой зоны.

Выразим Р*( r+e_0p)=M_rp получим

M≤M_crc=M₁+M₂=W_p1R_bt,ser+M_rp



8. В чем заключается расчет по образованию трещин наклонных к продольной оси элементов?
СНиП п4.11 – можно все оттуда

Трещины, появляющиеся в зоне действия поперечных сил, можно условно разделить на 2 группы. К первой относят трещины, начинающиеся от растянутой грани элемента в виде нормальных и затем, при дальнейшем развитии, получающие наклон по направлениям, перпендикулярным к траекториям главных растягивающих напряжений. Ко второй группе относят трещины, образующиеся в средней зоне по высоте элемента. Приведенный в нормах расчет по образованию трещин, наклонных к продольной оси элемента, относится именно к этим трещинам.

Для изгибаемых элементов расчет по образованию трещин, наклонных к продольной оси, можно не производить если выполняется условие

Q≤Q_b,crc

Q_b,crc – поперечное усилие, воспринимаемого бетоном в наклонном сечении.

В снипе расчет проводится согласно п.4.11

σ≤γ_b4R_bt,ser

9. На основании каких предпосылок производится расчет по раскрытию трещин? Какие фак­торы влияют на ширину раскрытия трещин?
Ширина раскрытия трещин, нормальных к продольной оси элемента, представляет собой разность удлинения арматуры и растянутого бетона на участке между трещинами длиной l_crc, т.е.

a_crc=ε_sml_crc- ε_btml_crc

Средней деформацией растянутого бетона ε_btm как величиной малой в сравнении со средней деформацией растянутой арматуры обычно пренебрегают и принимают

a_crc=ε_sml_crc

Вводя обозначение для отношения средних деформаций растянутой арматуры на участке между трещинами к деформациям арматуры в мечении с трещиной

Ѱ_s= ε_sm /ε_s<=1

Получают ширину раскрытия трещин на уровне оси растянутой арматуры

a_crc=Ѱ_sε_sl_crc= Ѱ_s(σ_s/E_s)l_crc

На ширину раскрытия трещин влияют: коэффициент Ѱ_s, в свою очередь, зависящий от прочности сцепления арматуры с бетоном, напряжения в арматуре сечения с трещиной σ_s, расстояние между трещинами l_crc. Значение этих факторов определяют расчетом.

Опыты показывают вследствие неоднородности структуры бетона при растяжении расстояния между трещинами могут отклоняться от средних значений в большую или меньшую сторону примерно в 1,5 раза.

Нормы рекомендуют определять ширину раскрытия трещин, нормальных к продольной оси элемента, на уровне оси растянутой арматуры по следующей эмпирической формуле (в миллиметрах)

a_crc=20(3,5-100µ)δηφ_l(σ_s/E_s)(кубический корень из d) – формула 4.14 снип жбк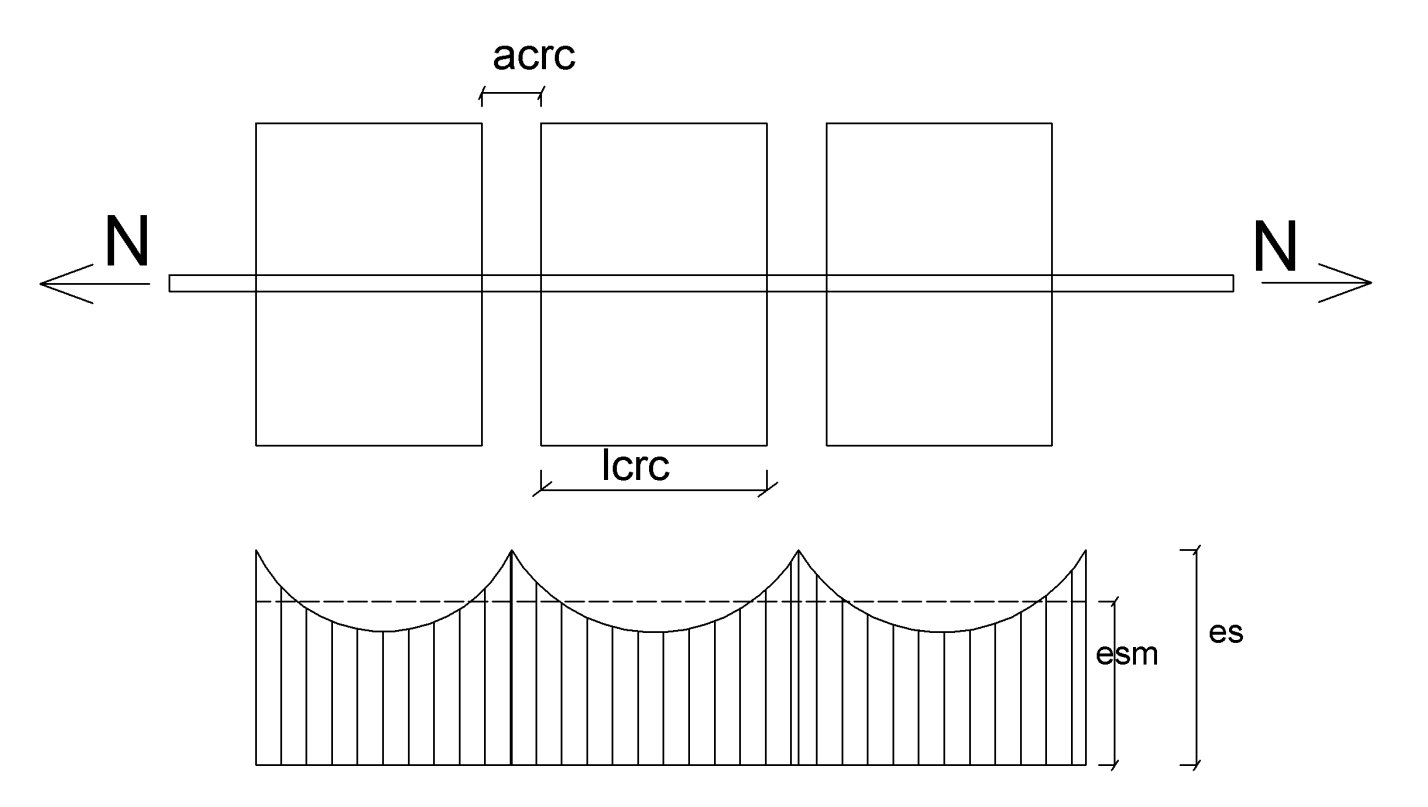



СНиП 4.14 ниже лежащий текст есть в СНиПе.

Ширина раскрытия трещин корректируется в следующих слу­чаях:

а) если центр тяжести сечения стержней крайнего ряда арматуры S изгибаемых, внецентренно сжатых, внецентренно растянутых при e_0,tot  0,8h₀ эле­ментов отстоит от наиболее растянутого волокна на расстоянии а₂ > 0,2h, значение a_crc должно быть увеличено путем умножения на коэффициент _a, равный:

δ_а=(20а₂/h-1)/3

и принимаемый не более 3;

б) для изгибаемых и внецентренно сжатых эле­ментов из тяжелого и легкого бетонов при . 0,008 и M_r2 < М₀ ширину раскрытия трещин от непродолжительного действия всех нагрузок допу­скается определять по линейной интерполяции между значением a_crc = 0 при моменте М_crc и значени­ем a_crc вычисленным согласно указаниям настояще­го пункта при моменте M₀ = М_crc + bh² R_bt,ser,где  = 15 /, но не более 0,6. При этом ширина продолжительного раскрытия трещин от действия постоянных и длительных нагрузок определяется путем умножения найденного значения a_crc от дей­ствия всех нагрузок на отношение

φ_l1(M_r1 - M_rp)/( M_r2 - M_rp)

где φ_l1=1,8 φ_lМ_crc/M_r2 но не менее _l.

Здесь ,  — то же, что и в формуле (144);

M_r1, M_r2  моменты M_r соответственно от дейст­вия постоянных и длительных и от всех нагрузок (см. п. 4.5);

в) для элементов из легкого и поризованного бетонов классов В7,5 и ниже значение a_crc должно быть увеличено на 20 %.