Ответы по железобетонным конструкциям. 1. Какие требования предъявляют к трещиностойкости железобетонной конструкции и как они делятся по категориям Охарактеризуйте категории трещиностойкости

Название	1. Какие требования предъявляют к трещиностойкости железобетонной конструкции и как они делятся по категориям Охарактеризуйте категории трещиностойкости
Анкор	Ответы по железобетонным конструкциям.doc
Дата	03.02.2017
Размер	2.43 Mb.
Формат файла
Имя файла	Ответы по железобетонным конструкциям.doc
Тип	Документы #1893
страница	2 из 4

1 2 3 4

10. В чем заключается физическая трактовка ширины раскрытия трещины в бетоне растянутой зоны?
Сущность расчета по раскрытию трещин, нормальных и наклонных к продольной оси, заключается в определении ширины раскрытия трещин на уровне растянутой арматуры a_crc и сравнении ее с предельно шириной раскрытия [a_crc]

Ширина раскрытия трещин, нормальных к продольной оси элемента, представляет собой разность удлинения арматуры и растянутого бетона на участке между трещинами длиной l_crc, т.е.

a_crc=ε_sml_crc- ε_btml_crc

Средней деформацией растянутого бетона ε_btm как величиной малой в сравнении со средней деформацией растянутой арматуры обычно пренебрегают и принимают

a_crc=ε_sml_crc

Вводя обозначение для отношения средних деформаций растянутой арматуры на участке между трещинами к деформациям арматуры в мечении с трещиной

Ѱ_s= ε_sm/ε_s<=1

Получают ширину раскрытия трещин на уровне оси растянутой арматуры

a_crc=Ѱ_sε_sl_crc= Ѱ_s(σ_s/E_s)l_crc

На ширину раскрытия трещин влияют: коэффициент Ѱ_s, в свою очередь, зависящий от прочности сцепления арматуры с бетоном, напряжения в арматуре сечения с трещиной σ_s, расстояние между трещинами l_crc. Значение этих факторов определяют расчетом.

Опыты показывают вследствие неоднородности структуры бетона при растяжении расстояния между трещинами могут отклоняться от средних значений в большую или меньшую сторону примерно в 1,5 раза.

Нормы рекомендуют определять ширину раскрытия трещин, нормальных к продольной оси элемента, на уровне оси растянутой арматуры по следующей эмпирической формуле (в миллиметрах)

a_crc=20(3,5-100µ)δηφ_l(σ_s/E_s)(кубический корень из d) – формула 4.14 снип жбк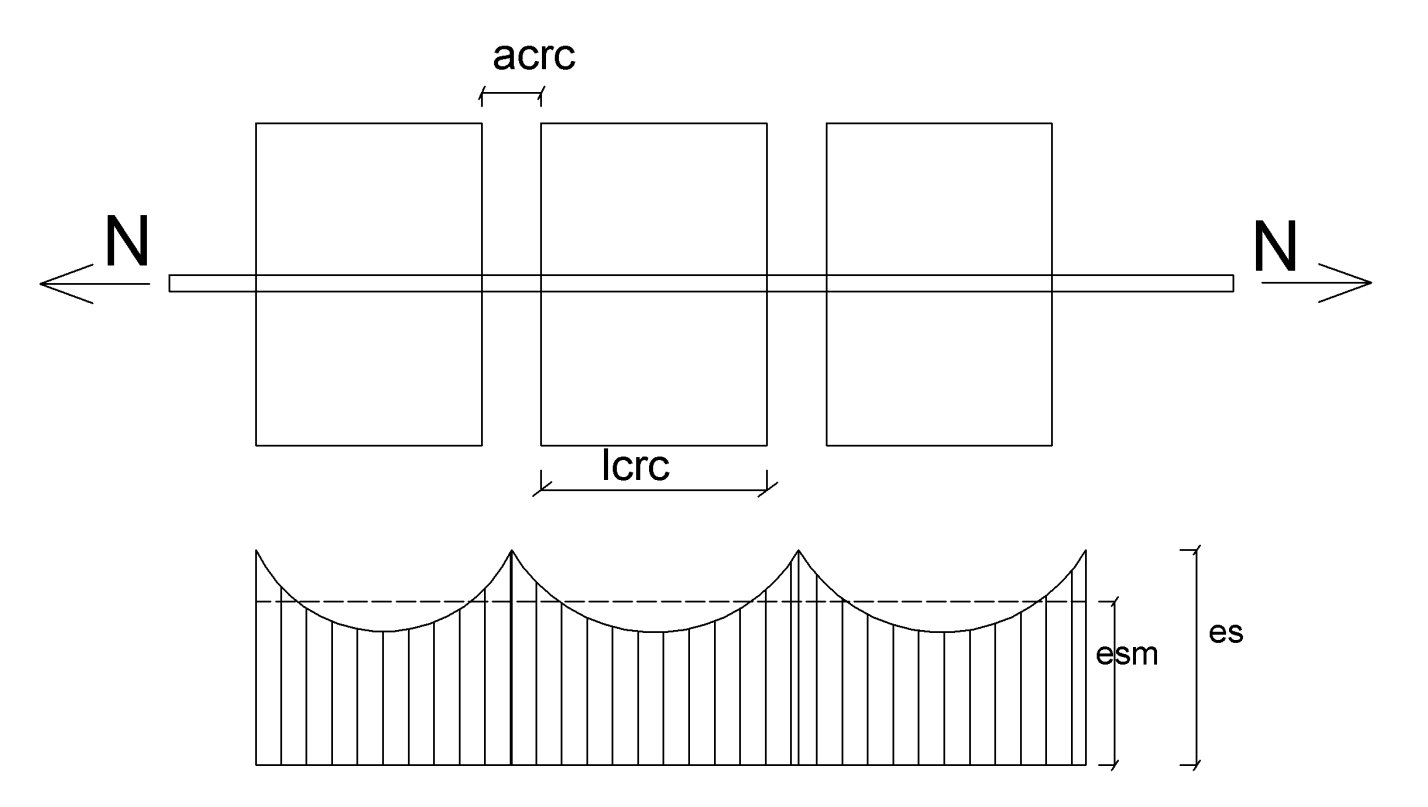

11. ОТ КАКИХ ФАКТОРОВ ЗАВИСИТ ШИРИНА РАСКРЫТИЯ ТРЕЩИН НОРМАЛЬНЫХ К ОСИ СОГЛАСНО ЭМПИРИЧЕСКОЙ ФОРМУЛЕ НОРМ?
[п. 4.14. СНиП ЖБК] Ширину раскрытия трещин, нормальных к продольной оси элемента a_crc, мм* следует определять по формуле:

α_crc=*_l**(σ_s/E_s)*20(3.5-100μ)³√d, где

Таким образом, расчет ширины раскрытия нормальных трещин зависит, в явной форме от напряжений в растянутой арматуре, коэффициента армаирования сечения, вида и диаметра арматуры и продолжительност действия нагрузки.

  коэффициент, принимаемый равным для элементов:

изгибаемых и внецентренно

сжатых ..................................... 1,0

растянутых............................... 1,2

_l  коэффициент, принимаемый равным при учете:

кратковременных нагрузок и

непродолжительного действия

постоянных и длительных

нагрузок ......................................................1,00

многократно повторяющейся

нагрузки, а также

продолжительного действия

постоянных и длительных

нагрузок для конструкций из бетона:

тяжелого:

естественной

влажности ....................... _l = 1,60 – 15

в водонасыщенном

состоянии .......................................... 1,20

при попеременном

водонасыщении и высушивании ..... 1,75

мелкозернистого групп:

А ......................................................... 1,75

Б ......................................................... 2,00

В ......................................................... 1,50

легкого и поризованного ........ не менее 1,50

ячеистого.................................................. 2,50

значение _l для мелкозернистого, легкого, поризованного и ячеистого бетонов в водонасыщенном состоянии умножают на коэффициент 0,8, а при попеременном водонасыщении и высушивании — на коэффициент 1,2;

 — коэффициент, принимаемый равным:

- при стержневой арматуре

периодического профиля .................1,0

стержневой арматуре гладкой .........1,3

- проволочной арматуре

- периодического профиля и

канатах .............................................1,2

гладкой арматуре ............................1,4

_s — напряжение в стержнях крайнего ряда арматуры S или (при наличии предварительного напряжения) приращение напряжений от действия внешней нагрузки, определяемое согласно указаниям п. 4.15;

 — коэффициент армирования сечения, принимаемый равным отношению площади сечения арматуры S к площади сечения бетона (при рабочей высоте h₀ и без учета сжатых свесов полок), но не более 0,02;

d — диаметр арматуры, мм.

12. КАКОВЫ ПРЕДПОСЫЛКИ РАСЧЕТА РАССТОЯНИЯ МЕЖДУ ТРЕЩИНАМИ В РАСТЯНУТОЙ ЗОНЕ ПРИ ЦЕНТРАЛЬНОМ РАСТЯЖЕНИИ, ПРИ ИЗГИБЕ? КАКОВЫ ПРЕДПОСЫЛКИ РАСЧЕТА КОЭФФИЦИЕНТА, ХАРАКТЕРИЗУЮЩЕГО РАБОТУ БЕТОНА НА РАСТЯЖЕНИЕ НА УЧАСТКЕ МЕЖДУ ТРЕЩИНАМИ ПРИ ЦЕНТРАЛЬНОМ РАСТЯЖЕНИИ, ПРИ ИЗГИБЕ?
Первые трещины по длине элемента появляются вследствие неоднородной прочности бетона в наиболее слабом месте.

По мере удаления от краев трещины растягивающее напряжение в бетоне увеличивается, и там, где оно достигает значения σ_bt=R_bt_,_ser появляется смежная трещина, расположенная на расстоянии l_crc от первой.

Приращение напряжения в растянутой арматуре после погашения обжатия в бетоне и появления трещины σ_scrc обусловлено передачей дополнительного усилия на арматуру с треснувшего бетона. Поскольку при переходе состояния сечения из стадии I в стадию II растягивающая сила одна и та же (N=N_crc), согласно выражению

N_crc=R_bt,ser(A+2αA_s)+P и формуле σ_sp=(N-P)/A_sp

σ_scrc=(N-P)/A_sp= R_bt,serА/A_sp+ 2α R_bt,ser (7.64)

Расстояние между трещинами l_crc находят из условия, что разность усилий в растянутой арматуре в сечениях с трещиной и в сечениях между трещинами уравновешивается усилием сцепления арматуры с бетоном.

Тогда (σ_sp+ σ_scrc)A_sp-(σ_sp+2α R_bt_,_ser) A_sp=τ_cdl_crcw (7.65)

где τ_c — максимальное напряжение сцепления арматуры с бетоном;

α —периметр сечения арматуры; w — коэффициент полноты эпюры сцепления.

После подстановки в уравнение (7.65) значения σ_scrc из формулы (7.64) получают

R_bt_,_ser A= τ_cdlw (7.66)

отсюда расстояние между трещинами l_crc= R_bt_,_ser A/ τ_cαw (7.67)

Если обозначить

R_bt_,_ser A/ τ_cw =η; A_sp/α=u; A_sp/А=μ (7.68)

то окончательно l_crc=(u/ μ₁) η (7 69)

На основании опытных данных выявлено, что коэффициент η зависит от вида и профиля арматуры. Расстояние между трещинами l_crc в элементах без предварительного напряжения определяют также по формуле (7.69), но в расчете вместо площади сечения напрягаемой арматуры A_SP принимают площадь сечения арматуры A_s.
Определение расстояния между трещинами при изгибе:

Приращение напряжений в растянутой арматуре, после того как момент внешних сил М превысит момент усилия предварительного обжатия М_rр, в сечении с трещиной σ_crc (как только она появилась), находят из условия, что при переходе состояния сечения из стадий I в стадию II изгибающий момент один и тот же, М_сгс.

Тогда σ_crc=( М_с_r_с- М_rpW_s)= R_bt_,_serW_pl/W_s

W_s – упругопластический момент сопротивления после образования трещин по растянутой зоне.

Расстояние между трещинами в зоне чистого изгиба l_crc, определяют, как и при центральном растяжении, из условия, что разность усилий в растянутой арматуре в сечениях с трещиной и между трещинами уравновешивается усилием сцепления арматуры с бетоном.

Тогда (σ_sp+ σ_scrc)A_sp-(σ_sp+2α R_bt_,_ser) A_sp=τ_cal_crcw

После подстановки значения σ_crc по (7.107) получают (W_pl/W_s-2α) R_bt_ser A_SP= τ_cal_crcw

Отсюда расстояние между трещинами l_crc=[(W_pl/W_s-2α) R_bt_ser A_SP]/ τ_cw (7.108) или

l_crc =k₁αuη , (7.109)

где k1=W_pl/aW_s-2 (7.110)

a, u, n имеют такие же значения, как и при центральном растяжении.

Расстояние между трещинами в элементах без предварительного напряжения также определяют по формуле l_crc =k₁αuη.
Работу бетона в центрально растянутых элементах на растяжение на участке между трещинами и связанную с ней неравномерность деформаций и напряжений арматуры учитывают в расчете коэффициентом ψ_s

ε_sm = ψ_sε_s; o_sm = ψ_s σ_s.

_s — коэффициент, учитывающий работу растянутого бетона на участке с трещинами и определяемый согласно указаниям п. 4.29; Коэффициент _s для элементов из тяжелого, мелкозернистого, легкого бетонов и двуслойных предварительно напряженных конструкций из ячеистого и тяжелого бетонов определяется по формуле

ψ_s=1.25-φ_ls*φ_m-(1- φ_m²)/[(3.5-1.8φ_m)e_s,tot/h] .

В предварительно напряженных изгибаемых элементах бетон начинает работать на растяжение лишь после того, как момент внешних сил превысит момент усилия предварительного обжатия М_r_р. Отсюда ψ_s=1-w_tχM_b_,_crc/(M-M_rp); (7.73)

Произведение w_tχ по данным опытов принимают: при кратковременном действии нагрузки — 0,8; при длительном действии нагрузки — 0,4. Коэффициент может изменяться от 0,3...0,5 до значения, близкого к единице. Под влиянием ползучести бетона растянутой зоны, как показали исследования, коэффициент ψ_s увеличивается. При многократно повторяющихся и динамических нагрузках ψ_s-1.

Нормы рекомендуют определять коэффициент ψ_s для изгибаемых и внецентренно загруженных элементов по эмпирической формуле

ψ_s=1.25-φ_ls*φ_m-(1- φ_m²)/[(3.5-1.8φ_m)e_s,tot/h]

13. КАК ОПРЕДЕЛЯЮТ НАПРЯЖЕНИЕ В БЕТОНЕ И АРМАТУРЕ В СЕЧЕНИЯХ С ТРЕЩИНОЙ?

Приращение напряжений в растянутой арматуре (после превышения усилием от внешней нагрузки усилия обжатия) в сечении с трещиной составляет:

σ_sp=(N-P)/Asp;

напряжение арматуры в элементе без предварительного напряжения в сечении с трещиной

σ_s=N/As.

В изгибаемом элементе после образования трещин бетон растянутой зоны в сечении с трещиной не работает.

При анализе напряженного состояния при отсутствии предварительного напряжения исходят из следующих положений:

1) в зоне чистого изгиба средние сечения, расположенные между трещинами и испытывающие слева и справа симметричные воздействия, после изгиба остаются плоскими;

2) зависимость между высотой сжатой зоны в сечении с трещинами χ и средней высотой сжатой зоны выражается эмпирической формулой φ=χ/χ_m=1-0.7/(100μ+1);

3) участок бетона растянутой зоны над трещиной в расчете не учитывается; влияние этого участка в некоторых случаях существенно, однако необходимые данные для практического учета этого фактора пока не накоплены.

Исходя из этих положений напряжения в бетоне и арматуре сжатой зоны сечения с трещиной выражают через напряжения в растянутой арматуре σ_s и определяют высоту сжатой зоны.

Высоту сжатой зоны в сечении с трещиной по приведенным формулам определяют приближенно, однако на результаты расчета раскрытия трещин, кривизн, прогибов и т. п. это не оказывает существенного влияния.

Плечо внутренней пары сил для таврового сечения при прямоугольной эпюре напряжений в бетоне сжатой зоны равно расстоянию между точками приложения усилия в растянутой арматуре и равнодействующей усилий в бетоне н арматуре сжатой зоны (см. рис. 7.9). Его можно определить из отношения статического момента площади приведенного сечения сжатой зоны S_red относительно оси, проходящей через центр тяжести сечения растянутой арматуры, к плошади приведенного сечения:

z₁=S_red/A_red=[s_b+(αν)A_s’(h₀-a’)]/(φ_f+ε)bh₀

После преобразований:

z₁=h₀[1-[(h_f’/h₀)φ_f+ζ²]/[2(φ_f+ζ)]

Напряжение в бетоне сжатой зоны в сечении с трещиной находят из условия равенства моментов внешних сил и усилия предварительного обжатия Р моменту внутренних усилий относительно оси, проходящей через центр тяжести сечения растянутой арматуры: M_s =σ_b(φ_f+ζ) bh₀z₁, (7.96)

откуда σ_b= M_s /(φ_f+ζ) bh₀z₁ = M_s/W_c (7.97)

Знаменатель выражения (7.97) представляет собой упругопластический момент сопротивления после образования трещин по сжатой зоне: W_s =(φ_f+ζ) bh₀z₁

Приращение напряжения в растянутой арматуре, после того как момент внешних сил превысит момент усилия предварительного обжатия, находят из уравнения моментов в сечении с трещиной: M_s-N_totz₁=σ_sA_spz₁ (7.99)

σ_s = (M_s-N_totz₁)/ A_spz₁ (7.100)

Знаменатель выражения (7.100) представляет собой упругопластический момент сопротивления после образования трещин по растянутой зоне:

W_s =A_SP z₁. (7.101)

Окончательно:

для изгибаемых элементов σ_s = [M-P(z₁-e_sp)]W_s; (7.102)

для внецентренно сжатых элементов σ_s = [N(e-z₁)-P(z₁-e_sp)]/W_s (7 .103)

для внецентренно растянутых элементов σ_s = [N(e+z₁)-P(z₁-e_sp)]/W_s (7.104)

Для внецентренно растянутых элементов при e_s_,_tot<0,8h₀ значение σ_s определяют по формуле (7.104), принимая z₁ равным z_s — расстоянию между центрами тяжести растянутой и сжатой арматуры.

Для изгибаемых элементов без предварительного напряжения:

σ_b=M/W_c (7.105)

σ_s=M/W_s (7.106)

14. КАК УЧИТЫВАЕТСЯ В РАСЧЕТАХ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫХ ЭЛЕМЕНТОВ ВЛИЯНИЕ НАЧАЛЬНЫХ ТРЕЩИН В БЕТОНЕ СЖАТОЙ ЗОНЫ?
В расчетах предварительно напряженных элементов по второй группе предельных состояний необходимо учитывать влияние трещин, которые возникают в зоне, впоследствии сжатой под действием внешней нагрузки. Такие начальные трещины могут появиться при изготовлении и предварительном обжатии, транспортировании и монтаже элементов. Они снижают трещиностойкость и жесткость элементов.

Расчет по образованию трещин для элементов с начальными трещинами.

Значение М_CRC снижается на ΔM_crc=λ M_crc

На основании теоретических и опытных данных коэффициент λ=(1.5-0.9/δ)(1-φ_m)

δ=[y/(h-y)][A_sp/(A_sp+A_sp’)]

где у — расстояние от центра тяжести приведенного сечения до грани, растянутой при действии внешней нагрузки.

Для конструкций, армированных проволокой, значения δ снижают на 15 % ; φ_m — определяют по формуле (7.75: φ_m= R_bt_,_serW_pl/[M_z-M_zp]), но принимают не менее 0,45.

Расчет по раскрытию трещин в элементах с начальными трещинами.

Значение Р снижается на ΔР: ΔP=λP (7.141)

Проверяют и глубину начальной трещины h_crc = h — (1,2 + φ_m) ζh₀ ≤ 0,5h,

где ζ — высота сжатой зоны от действия внешней нагрузки и усилия предварительного обжатия, определяемая по формуле (7.90);

Расчет по закрытию трещин в элементах, имеющих начальные трещины в сжатых зонах.

Значение Р уменьшают умножением на коэффициент, равный 1,1(1—λ) но значение должно быть не более 1; значение λ определяют по формуле (7.140).

Расчет перемещений железобетонных элементов с начальными трещинами в сжатой зоне. Значения кривизн увеличивают на 5%, а значения (1/r)₄ — на 25%. На участках с трещинами усилия Р, уменьшают на ΔР.

15. ОСОБЕННОСТИ РАСЧЕТА ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫХ КОНСТРУКЦИЙ ПО ЗАКРЫТИЮ ТРЕЩИН. КАКИЕ ТРЕБОВАНИЯ К РАСЧЕТУ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОГО ЭЛЕМЕНТА ПО ЗАКРЫТИЮ ТРЕЩИН В РАСТЯНУТЫХ ЗОНАХ?

[СНиП ЖБК]

4.19. Для обеспечения надежного закрытия трещин, нормальных к продольной оси элемента, при действии постоянных и длительных нагрузок должны соблюдаться следующие требования:

а) в напрягаемой арматуре S от действия постоянных, длительных и кратковременных нагрузок не должны возникать необратимые деформации, что обеспечивается соблюдением условия σ_sp+σ_s≤0.8R_s_,_ser (154)

где _s  приращение напряжения в напрягаемой арматуре S от действия внешних нагрузок, определяемое по формулам (146)—(148);

б) сечение элемента с трещиной в растянутой зоне от действия постоянных, длительных и кратковременных нагрузок должно оставаться обжатым при действии постоянных и длительных нагрузок с нормальными напряжениями сжатия _b на растягиваемой внешними нагрузками грани элемента не менее 0,5 МПа, при этом величина _b определяется как для упругого тела от действия внешних нагрузок и усилия предварительного обжатия.

4.20. Для участков элементов, имеющих начальные трещины в сжатой зоне (см. п. 1.18), значение _spв формуле (154) умножается на коэффициент, равный 1 — , а величина Р при определении напряжения _b умножается на коэффициент, равный 1,1 (1 —), но не более 1,0, где значения  определяются согласно указаниям п. 4.6*.

Расчет по закрытию трещин,

наклонных к продольной оси элемента

4.21. Для обеспечения надежного закрытия трещин, наклонных к продольной оси элемента, оба главных напряжения в бетоне, определяемые согласно указаниям п. 4.11 на уровне центра тяжести приведенного сечения при действии постоянных и длительных нагрузок, должны быть сжимающими и по величине не менее 0,6 МПа.

Указанное требование обеспечивается с помощью предварительно напряженной поперечной арматуры (хомутов или отогнутых стержней).

16. ЦЕЛЬ РАСЧЕТА ПО ПЕРЕМЕЩЕНИЯМ.
Цель расчета по деформациям сводится к определению величин деформаций, которые могут иметь место в элементах проектируемых конструкций в процесе их длительной эксплуатации и сравнению полученных данных с допустимыми предельными величиными:

f  f_u,

где f – прогиб от расчетных нагрузок при _f = 1;

f_u – допустимый нормами предельный прогиб, принимаемый по СНиП 2.01.07-85*.

Величина кривизны и деформаций элементов отсчитывается от их начального состояния, при наличии предварительного напряжения – от состояния до обжатия.

Для участков элементов, где в растянутой зоне не образуются трещины, нормальные к продольной оси элемента, кривизна определяется как для сплошного тела.

Для участков элемента, где в растянутой зоне имеются трещины нормальные к продольной оси кривизна определяется как отношение разности средних деформаций крайнего волокна сжатой зоны бетона и продольной растянутой арматуры к рабочей высоте сечения элемена.

Элементы или участки элементов рассматриваются без трещин в растянутой зоне, если трещины не образуются придействии полных нагрузок или если он закрыты при действии постоянных и временных длительных нагрузок.

17. КАК ОПРЕДЕЛИТЬ ПРОГИБ ЖЕЛЕЗОБЕТОННОГО ЭЛЕМЕНТА, НЕ ИМЕЮЩЕГО ТРЕЩИН В РАСТЯНУТЫХ ЗОНАХ?
[СНиП п 4.22] Полное значение прогиба железобетонного элемента, не имеющего трещин в растянутой зоне, определиться по формуле

f = f₁ + f₂ - f₃ - f₄,

где f₁ – прогиб от кратковременной нагрузки;

f₂ – прогиб от постоянной и длительно действующей нагрузки;

f₃ – выгиб от кратковременного действия усилия предварительного обжатия P;

f₄ – выгиб вследствие ползучести бетона от обжатия.

Нормы рекомендуют вычислять прогибы по кривизне, используя интеграл Мора: f_m=₀¹∫M_x(1/r)_xdx

Где Mx - изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб;

(1/r)_x — полная кривизна элемента в сечении х от нагрузки, при которой определяется прогиб.

Для однопролетной балки постоянного сечения: f=φ_m*l₀²*(1/r)

где _m – коэффициент, зависящий от условий опирания и схемы загружения элемента.

Выгиб предварительно напряженных элементов постоянной высоты, вызванный внецентренным обжатием: f₃=Pe₀_Pl²/8B.

Выгиб предварительно напряженных элементов постоянной высоты, вызванный ползучестью бетона от обжатия: f₄=(1/r)₄l²/8.

Прогиб изгибаемых элементов без предварительного напряжения — плит, панелей, балок и т.п. — от равномерно распределенной нагрузки: f=(5/384)(ql₄/B).

Прогиб однопролетных балок и консолей от различных нагрузок определяют по кривизне или жесткости в сечении с максимальным моментом по общей формуле:

f = sl²(1/2) или f= sl²(М/В).

Здесь коэффициент s зависит от расчетной схемы элемента и вида нагрузки.

Прогиб коротких изгибаемых элементов при отношении l/h< 10 (подкрановых балок, подстропильных балок и т. п.) необходимо определять с учетом влияния поперечных сил. В этом случае полный прогиб равен сумме прогибов, обусловленных деформациями изгиба и сдвига:

f_q=₀^l∫Qγ_xdx; γ_x=[(1.5Qφ_b₂)/(Gbh₀)]/φ_crc.

18. ИЗ ЧЕГО СКЛАДЫВАЕТСЯ ПОЛНЫЙ ПРОГИБ И КРИВИЗНА ЭЛЕМЕНТОВ ПРИ ОТСУТСТВИИ ТРЕЩИН В РАСТЯНУТОЙ ЗОНЕ? ЗАПИШИТЕ РАСЧЕТНЫЕ ФОРМУЛЫ.
[Лекции СНиП п 4.22-4.31] Полное значение прогиба и кривизны железобетонного элемента, не имеющего трещин в растянутой зоне, складывается из: f = f₁ + f₂ - f₃ - f₄,

где f₁ – прогиб от кратковременной нагрузки;

f₂ – прогиб от постоянной и длительно действующей нагрузки;

f₃ – выгиб от кратковременного действия усилия предварительного обжатия P;

f₄ – выгиб вследствие ползучести бетона от обжатия.

Нормы рекомендуют вычислять прогибы по кривизне, используя интеграл Мора: f_m=₀¹∫M_x(1/r)_xdx

Где Mx - изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб;

(1/r)_x — полная кривизна элемента в сечении х от нагрузки, при которой определяется прогиб.

Для однопролетной балки постоянного сечения: f=φ_m*l₀²*(1/r)

где _m – коэффициент, зависящий от условий опирания и схемы загружения элемента.

19. ФАКТОРЫ ВЛИЯЮЩИЕ НА ПРОГИБЫ ЖЕЛЕЗОБЕТОННЫХ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПРИ ОТСУТСТВИИ И НАЛИЧИИ ТРЕЩИН В РАСТЯНУТОЙ ЗОНЕ.
Факторы:

— кривизна от непродолжительного действия всей нагрузки, на которую производится расчет по деформациям;

— кривизна от непродолжительного действия постоянных и длительных нагрузок;

— кривизна от продолжительного действия постоянных и длительных нагрузок;

— кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия.
[Лекции СНиП п 4.22-4.31] Факторы влияющие на прогибы железобетонных изгибаемых элементов при отсутствии трещин в растянутой зоне:

– прогиб от кратковременной нагрузки;

– прогиб от постоянной и длительно действующей нагрузки;

– выгиб от кратковременного действия усилия предварительного обжатия P;

– выгиб вследствие ползучести бетона от обжатия.

4.32. Для изгибаемых элементов при 1/h<10 необходимо учитывать влияние поперечных сил на их прогиб.

_b₁ — коэффициент, учитывающий влияние кратковременной ползучести бетона;

_b₂ — коэффициент, учитывающий влияние длительной ползучести бетона на деформации элемента без трещин

_b, ’_b — относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия и определяемые соответственно на уровне центра тяжести растянутой продольной арматуры и крайнего сжатого волокна бетона.

Прогибы и кривизны ЖБК с трещинами в растянутой зоне

После появления трещин в растянутой зоне изгибаемый элемент будет разделен на отдельные блоки, которые соединяются между собой растянутой арматурой и сжатым бетоном. Нейтральная ось в таком случае будет волнообразной. Деформации укорочения сжатой зоны бетона неравномерны. Они имеют наибольшую величину над трещиной и существенно меньшую над серединами блоков.

Напряжения в растянутой арматуре будут наибольшими в сечении с трещиной, а по мере удаления от трещины уменьшаются за счет передачи растягивающего усилия на бетон.

20. КАК ОПРЕДЕЛИТЬ ПРОГИБ ЖЕЛЕЗОБЕТОННОГО ЭЛЕМЕНТА С ТРЕЩИНАМИ В РАСТЯНУТОЙ ЗОНЕ? КАК УЧИТЫВАЮТ ПРИ ОПРЕДЕЛЕНИИ ПРОГИБА ВЛИЯНИЕ ДЛИТЕЛЬНОГО ДЕЙСТВИЯ НАГРУЗКИ?
Определение прогибов

К элеменетам, не имеющим трещин в растянутой зоне, относятся преднапряженные конструкции 1й и 2й катеорий трещностойкости и конструкции со слабым армированием, прочность которых исчерпывается с образованием трещин в растянутой зоне.
4.31. Прогиб f_m, обусловленный деформацией изгиба, определяется по формуле

f_m=₀¹∫M_x(1/r)_xdx (171)

где Mx изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб;

(1/r)_x — полная кривизна элемента в сечении х от нагрузки, при которой определяется прогиб; значения 1/r определяются по формулам (155) и (170) соответственно для участков без трещин и с трещинами; знак 1/r принимается в соответствии с эпюрой кривизны.

Для сплошных балочных плит толщиной менее 25 см с трещинами в растянутой зоне значения прогибов (формула 171) повышают умножением на коэффициент ФИ:

φ= (h₀ / (h₀ – 0.7)) ^3 ≤ 1.5

Полный прогиб элементов определяют с с учетом длительности действий нагрузки f=f1-f2+f3-f4, где f1 – прогиб от непродольнительно действия всей нагрузки, f2 – прогиб от непрод. lействия постоянной и длительной , f3 – от прод-ого действия постояннрой и и длит., f4 – выгиб, вызванный ползучестю бетона от обжатия.

Полный прогиб преднапряженных элементов определяют с учетом длительности действия нагрузки по полной кривизне

1/r = 1/r1 - 1/r2 + 1/r3 - 1/r4/

Для изгибаемых элементов постоянного сечения без предварительного напряжения арматуры, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента/

21. Предпосылки, заложенные в основу определения кривизны изгибаемого элемента с трещинами в растянутой зоне.
Кривизну железобетонных элементов на участках, где образуются нормальные трещины в растянутой зоне, определяют на основе следующих положений:

рассматривают сечение с трещиной в растянутой зоне;
работу растянутого бетона, расположенного между нулевой линией и вершиной трещины, не учитывают и считают, что все растягивающие усилия в сечении с трещиной воспринимаются продольной арматурой;
в расчет вводят высоту сжатой зоны над трещиной и принимают, что напряжения в бетоне сжатой зоны распределены равномерно, а неупругие деформации сжатого бетона (имеются в виду деформации ползучести) учитываются коэффициентом ν_b;
переход от деформаций арматуры и бетона в сечении с трещиной к средним деформациям осуществляют путем введения в расчет коэффициентов φs и φb, учитывающих соответственно работу растянутого бетона на участке с трещинами и неравномерность распределения деформаций крайних сжатых волокон бетона по длине участка с трещинами.

22. Каким образом можно вывести кривизну оси при изгибе предварительно напряженного элемента на участках с трещинами?
На участках, где образуются нормальные к продольной оси элемента трещины в стадии II, общее деформированное состояние определяют средними деформациями растянутой арматуры E_sm и средними деформациями бетона сжатой зоны E_bm и средним положением нейтральной оси с радиусом кривизны r.

Для железобетонного элемента в зоне чистого изгиба кривизна оси и средние деформации арматуры и бетона связаны зависимостью:

L_crc / r= E_sm l_crc/(h_o-x_m)= E_bm l_crc/x_m=( E_sm+ E_bm)l_crc/h_o.

После сокращения на l_crc кривизна оси при изгибе представляется как тангенс угла наклона на эпюре средних деформаций:

1/r=Esm/(ho-xm)=Ebm/xm=(Esm+Ebm)/ho.

Esm=ψs σs/Es, Ebm=ψb σb/ν Eb.

Кривизна оси при изгибе:

1/r= ψs σs /(Es (ho-xm))= ψb σb/(ν Eb xm)=ψs σs/Es ho+ ψb σb/ν Eb ho.

После подстановки в это выражение значений напряжений в арматуре и бетоне σs = M/Ws; σb = M/Wc получим выражение для определения кривизны:

1/r= ψs M /(Es Ws (ho-xm))= ψb M/(ν Eb Wc xm)= M/ho *( ψs /(Es Ws) + ψb/(ν Eb Wc).

Выражение кривизны с учетом значений упругопластических моментов сопротивления Ws и Wc принимают следующий вид:

1/r= M/(ho z1)*( ψs /(Es As) + ψb/(ν Eb b ho (φf+ξ)).

В общем случае систему внешних сил и усилий предварительного обжатия заменяют эквивалентной системой с моментом Ms И суммарной продольной силой Ntot.

Напряжения в бетоне сжатой зоны и в растянутой арматуре:

σb = M/Аb z1, Ab=(φf+ξ)b ho, σs = Ms/(As+Аsp) z1-Ntot/(As+Asp).

Общее выражение кривизны оси при изгибе после подстановки значений напряжений в бетоне сжатой зоны и в растянутой арматуре принимает вид:

1/r= Ms/(ho z1)*( ψs /(Es (As+Asp)) + ψb/(ν Eb Ab)-Ntot* ψs/ho Es (As+Asp).

Кривизна оси при изгибе и жесткость на участках элементов с трещинами с течением времени изменяются, и поэтому в расчетах их определяют с учетом ряда физических факторов: работы бетона на растяжение на участках между трещинами, характеризуемой коэффициентом ψs, неравномерности деформаций бетона сжатой зоны на участках между трещинами, характеризуемой коэффициентом ψb, неупругих деформаций бетона

23. Как определяется полная кривизна железобетонного элемента с трещинами в растянутой зоне? Выведите формулы для определения кривизны изгибаемого элемента с трещинами в растянутой зоне.
На участках, где образуются нормальные к продольной оси элемента трещины в стадии II, общее деформированное состояние определяют средними деформациями растянутой арматуры E_sm и средними деформациями бетона сжатой зоны E_bm и средним положением нейтральной оси с радиусом кривизны r.

Для железобетонного элемента в зоне чистого изгиба кривизна оси и средние деформации арматуры и бетона связаны зависимостью:

Lcrc / r= E_sm lcrc/(ho-x_m)= E_bm lcrc/x_m=( E_sm+ E_bm)lcrc/ho.

После сокращения на lcrc кривизна оси при изгибе представляется как тангенс угла наклона на эпюре средних деформаций:

1/r=Esm/(ho-xm)=Ebm/xm=(Esm+Ebm)/ho.

Esm=ψs σs/Es, Ebm=ψb σb/ν Eb.

Кривизна оси при изгибе:

1/r= ψs σs /(Es (ho-xm))= ψb σb/(ν Eb xm)=ψs σs/Es ho+ ψb σb/ν Eb ho.

После подстановки в это выражение значений напряжений в арматуре и бетоне σs = M/Ws; σb = M/Wc получим выражение для определения кривизны:

1/r= ψs M /(Es Ws (ho-xm))= ψb M/(ν Eb Wc xm)= M/ho *( ψs /(Es Ws) + ψb/(ν Eb Wc)).

Знаменатель в этом выражении характеризует собой одну и ту же жесткость железобетонного сечения при изгибе:

По растянутой зоне B=(Es Ws/ ψs)*(ho-xm);

По сжатой зоне B=( ν Eb/ ψb) Wc xm;

По обеим зонам сечения B=ho/(ψs /(Es Ws) + ψb/(ν Eb Wc)).

Выражение жесткости с учетом значений упругопластических моментов сопротивления Ws и Wc принимают следующий вид:

B=ho z1/(ψs /(Es As) + ψb/(ν Eb b ho (φf+ξ))).

25. Основные требования к сборным железобетонным конструкциям зданий. Типизация сборных элементов, номенклатура и каталоги сборных элементов. Унификация размеров и конструктивных схем здания.
Индустриализация строительства – превращение строительства в ритмичный комплексно-механизированный, в будущем автоматизированный процесс.

Ограничение числа типоразмеров достигается путем унификации и типизации, которые является общими принципами современного строительного проектирования.

Унификация – приведение к единообразию основных размеров сооружений, габаритных схем, сборных элементов, их привязок к координационным осям, узлов сопряжения элементов, а также нагрузок.

Основой унификации является единая модульная система (ЕМС), предусматривающую градацию размеров на базе основного модуля 100 мм (или укрупненного кратного 100 мм).

На основе унифицированных размеров все многообразие объемно-планировочных решений сведено к ограниченному числу унифицированных габаритных схем, позволяющих удовлетворить практически все основные потребности наиболее распространенных производств.

Для одноэтажных промышленных зданий с мостовыми кранами расстояние между разбивочными осями в продольном направлении (шаг колонн) принято равным 6 или 12 м, а между разбивочными осями в поперечном направлении (пролеты здания) кратным укрупненному модулю 6 м, т.е. 18, 24, 30 м и т.д.Высота от пола до низа основной несущей конструкции принята кратной модулю 1.2 м, например 10,8;12м.

Для промышленных многоэтажных зданий унифицированной является сетка колонн 9*6, 12*6 м.

В гражданских зданиях модулем для сетки осей является размер 0,2 м.

Типизация элементов - для каждого конструктивного элемента здания отбирают наиболее рациональный, проверенный на практике, тип конструкции с наилучшими по сравнению с другими решениями технико-экономическими показателями. Выбранный таким образом тип элемента принимают для массового изготовления.

В результате работы по типизации составлены каталоги сборных железобетонных элементов, которыми руководствуются при проектировании различных зданий.

Предусмотрено три категории размеров типовых элементов зданий: номинальные, конструктивные, натуральные. Номинальные – расстояния между разбивочными осями в плане здания. Конструктивные размеры отличаются от номинальных на размер швов и зазоров. Натурные размеры элемента – фактические размеры, которые в зависимости от точности изготовления могут отличаться от конструктивных размеров на некоторую величину , называемую допуском.

Наряду с требованиями типизации и унификации при проектировании сборных конструкций должны учитываться требования технологичности при изготовлении и монтаже.

Технологичными называют элементы, конструкция которых допускает их массовое изготовление на заводе или полигоне с использованием высокопроизводительных машин и механизмов без трудоемких ручных операций и удобной установки и закрепления их в проектном положении на строительной площадке с наименьшими затратами труда при максимальном использовании машин и механизмов.

26. Компоновка конструктивной схемы здания, привязка элементов к разбивочным осям. Устройство температурно-деформационных швов.
Современные одноэтажные производственные здания в большинстве случаев решаются по каркасной схеме.

Каркас может быть образован из плоских элементов, работающих по балочной схеме (стропильных конструкций), либо включать в себя пространственную конструкцию покрытия (в виде оболочек, опертых на колонны).

Пространственный каркас условно расчленяют на поперечные и продольные рамы, каждая из которых воспринимает горизонтальные и вертикальные нагрузки.

Основным элементом каркаса является поперечная рама, состоящая из колонн защемленных в фундаментах, ригелей (ферма балка арка), покрытия над ними в виде плит.

Поперечная рама воспринимает нагрузку от массы снега, кранов, стен, ветра и обеспечивает жесткость здания в поперечном направлении.

В продольную раму включают один ряд колонн в пределах температурного блока и продольные конструкции, такие как подкрановые балки, вертикальные связи, распорки по колоннам, конструкции покрытия.

Продольная рама обеспечивает жесткость здания в продольном направлении и воспринимает нагрузки от продольного торможения кранов и ветра, действующего в торец здания.

В задачу компоновки конструктивной схемы входят:

Выбор сетки колонн и внутренних габаритов здания
Компоновка покрытия
Разбивка здания на температурные блоки
Выбор схемы связей, обеспечивающих пространственную жесткость здания
В целях обеспечения максимальной типизации элементов каркаса приняты следующие привязки к продольным и поперечным координационным разбивочным осям:

1. Наружные грани колонн и внутренние поверхности стен совмещаются с продольными разбивочными осями (нулевая привязка) в зданиях без мостовых кранов и в зданиях, оборудованных мостовыми кранами грузоподъемностью до 30 т включительно при шаге колонн 6 м и высоте от пола до низа несущих конструкций покрытия менее 16,2 м.

2. Наружные грани колонн и внутренние поверхности стен смещаются с продольных разбивочных осей наружу здания на 250 мм в зданиях, оборудованных мостовыми кранами грузоподъемностью до 50 т включительно при шаге колонн 6 м и высоте от пола до низа несущих конструкций покрытия 16,2 и 18 м, а также при шаге колонн 12 м и высоте от 8,4 до 18 м.

3. Колонны средних рядов (за исключением колонн, примыкающих к продольному температурному шву, колонн, установленных в местах перепада высот пролетов одного направления, а также кроме колонн при поперечных температурных швах и колонн, примыкающих к торцам зданий) располагают так, чтобы оси сечения подкрановой части колонны совпадали с продольными и поперечными разбивочными осями.

4. Геометрические оси торцовых колонн основного каркаса смещаются с поперечных разбивочных осей внутрь здания на 500 мм, а внутренние поверхности торцовых стен совпадают с поперечными разбивочными осями (нулевая привязка).

5. Перепады высот между пролетами одного направления и продольные температурные швы в зданиях с железобетонным каркасом следует осуществлять, как правило, на двух колоннах со вставкой.

6. Поперечные температурные швы осуществляют на парных колоннах. При этом ось температурного шва совмещается с поперечной разбивочной осью, а геометрические оси парных колонн смещаются с разбивочной оси на 500 мм.

7. В зданиях, оборудованных электрическими мостовыми кранами грузоподъемностью до 50 т включительно, расстояние от продольной разбивочной оси до оси подкранового рельса принимается равным 750 мм.

8. Примыкание двух взаимно перпендикулярных пролетов следует осуществлять на двух колоннах со вставкой размером 500 и 1000 мм.

Высота здания определяется по технологическим условиям и назначается исходя из верха кранового рельса.

С изменением температуры железобетонные конструкции деформируются — укорачиваются или удлиняются; вследствие усадки бетона — укорачиваются. При неравномерной осадке основания части конструкций взаимно смещаются в вертикальном направлении. В большинстве случаев железобетонные конструкции представляют собой статически неопределимые системы и поэтому от изменения температуры, усадки бетона, а также от неравномерной осадки фундаментов в них возникают дополнительные усилия, что может привести к появлению трещин или к разрушению части конструкции. Чтобы уменьшить усилия от температуры и усадки, железобетонные конструкции делят по длине и ширине температурно-усадочными швами на отдельные части — деформационные блоки. Температурно-усадочные швы выполняют в наземной части здания—от кровли до верха фундамента, разделяя при этом перекрытия и стены. Ширина температурно-усадочного шва составляет 20-30 мм. Осадочные швы, служащие одновременно и температурно-усадочными, устраивают между частями зданий разной высоты или в зданиях, возводимых на участке с разнородными грунтами; такими швами делят и фундаменты. Осадочные швы устраивают с помощью вкладного пролета из плит и балок.

Наибольшее допустимое расстояние между температурно-усадочными швами в железобетонных конструкциях нормируется и составляет в отапливаемых одноэтажных зданиям из сборного железобетона 72 м, в неотапливаемых – 48 м..

В ряде случаев целесообразно рассчитать температуру Δt и усадочные деформации Δsh: Δt=αbt ltb Δto; Δsh= αsh ltb; αbt=1*10-5 1/град

27. Классификация железобетонных фундаментов. Отдельные, ленточные и сплошные фундаменты, области их применения.

Делятся на: отдельные — под каждой колонной; ленточные — под рядами колонн в одном или двух направлениях, а также под несущими стенами; сплошные — под всем сооружением. Фундаменты возводят чаще всего на естественных основаниях (они преимущественно и рассмотрены здесь), но в ряде случаев выполняют и на сваях. В последнем случае фундамент представляет собой группу свай, объединенную поверху распределительной железобетонной плитой — ростверком.

Отдельные фундаменты устраивают при относительно небольших нагрузках и достаточно редком размещении колонн. Ленточные фундаменты под рядами колонн делают тогда, когда подошвы отдельных фундаментов близко подходят друг к другу, что обычно бывает при слабых грунтах и больших нагрузках. Целесообразно применять ленточные фундаменты при неоднородных грунтах и внешних нагрузках, различных по значению, так как они выравнивают неравномерные осадки основания. Если несущая способность ленточных фундаментов недостаточна или деформации основания под ними больше допустимых, то устраивают сплошные фундаменты. Они в еще большей мере выравнивают осадки основания. Эти фундаменты применяют при слабых неоднородных грунтах, а также при значительных и неравномерно распределенных нагрузках.

По способу изготовления фундаменты бывают сборные и монолитные.

28. Железобетонные фундаменты неглубокого заложения. Расчет центрально нагруженных фундаментов.
В зависимости от размеров сборные фундаменты колонн выполняют сборными и монолитными. Их выполняют из тяжелых бетонов классов В15...В25, устанавливают на песчано-гравийную уплотненную подготовку толщиной 100 мм. В фундаментах предусматривают арматуру, располагаемую по подошве в виде сварных сеток. Минимальную толщину защитного слоя арматуры принимают 35 мм. Если под фундаментом нет подготовки, то защитный слой делают не менее 70 мм.

Необходимая площадь подошвы центрально-нагруженного фундаментапри предварительном расчете

A=ab=(1,2…1,6)Ncol/(R-γ_md) R – расчетное давление на грунт; γ_mусредненная нагрузка от веса фундамента и грунта на его ступенях; D – глубина заложения фундамента

Минимальную высоту фундамента с квадратной подошвой определяют условным расчетом его прочности на продавливание в предположении, что оно может происходить по поверхности пирамиды, боковые стороны которой начинаются у колонн и наклонены под углом 45°. Это условие выражается формулой (для тяжелых бетонов)

P<=Rbt ho u_m

Продавливающую силу принимают согласно расчету по первой группе предельных состояний на уровне верха фундамента за вычетом давления грунта по площади основания пирамиды продавливания: P=N-A1 p.

P=N/A1; A1=(hc+2ho)(b_c+2h₀)

29. Железобетонные фундаменты неглубокого заложения. Особенности расчета внецентренно нагруженных отдельных фундаментов.
Внецентренно нагруженные фундаменты. Их целесообразно выполнять с прямоугольной подошвой, вытянутой в плоскости действия момента.

Соотношение сторон b/a=0,6…0,8. При том размеры сторон округляем в большую сторону до значения кратного 30 см при использовании металлической инвентарной опалубки и 10 см при неинвентарной опалубки.

Максимальное и минимальное давление под краем подошвы определяют из предположения линейного распределения напряжений в грунте:

Pmax min=Ntot/A+-Mtot/W=Ntot/ab(1+-b*eo/a)

Ntot Mtot – нормальная сила и изгибающий момент при гамма ф =1 на уровне подошвы фундамента.

Ntot=Ncol+A гамма м Н

Mtot=Mcol+Qcol H

Eo – эксцентриситет продольной силы относительно центра тяжести подошвы фундамента. Eo= Mtot/ Ntot

Максимальное краевое давление на грунт не должно превышать 1,2R а среднее давление – R.

В промышленных здания с мостовыми кранами Q<75 т принимают pmin>0, не допускается отрыв фундамента от грунта.

Высоту внецентренно нагруженного фундамента определяют из условия:

Ho=-hcol/2+0,5(Ncol/Rbt+P)^0,5

И конструктивных требований

Hsoc=>(1-1,5)hcol+0.05

Hsoc=>lan+0.05

Hsoc – глубина стакана

Lan – длина анкеровки арматуры колонны в стакане фундаментаю

Определив высоту фундамента из расчета на продавливание и конструктивных требования принимают большую из них.

При h<450 мм фундамент выполняют одноступенчатым, при 450

1 2 3 4