билеты по физике. Документ. 1. Кинематика поступательного движения материальной точки (радиусвектор, скорость, ускорение, перемещение, путь)
 Скачать 7.42 Mb.
|
|
1. Кинематика поступательного движения материальной точки (радиус-вектор, скорость, ускорение, перемещение, путь) Кинематика - раздел физики, изучающий движение тел, не интересуясь причинами, обуславливающие это движение. Механи́ческое движе́ние - это изменение положения телав пространстве относительно других тел с течением времени. (механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением) Материальная точка - тело, размерами которого, в условиях данной задачи, можно принебреч. Абсолютно твердое тело - тело, деформацией которого можно принебреч, в условиях данной задачи. Путь - скалярная величина, характеризующая длинну траектории движения тела. Перемещение - нравленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение (векторная величина) Скорость: -векторная величина, характеризующая быстроту пермещения частицы по траектории, в который движется эта частица в каждый момент времени. -производная радиуса вектора частицы по времени. -производная от перемещения по времени. Ускорение: -векторная величина, характеризующая быстроту изменения вектора скорости. -производная от скорости по времени. -производная от скорости по времени.  Траектория - некоторая линия, описываемая движение мат. точки. 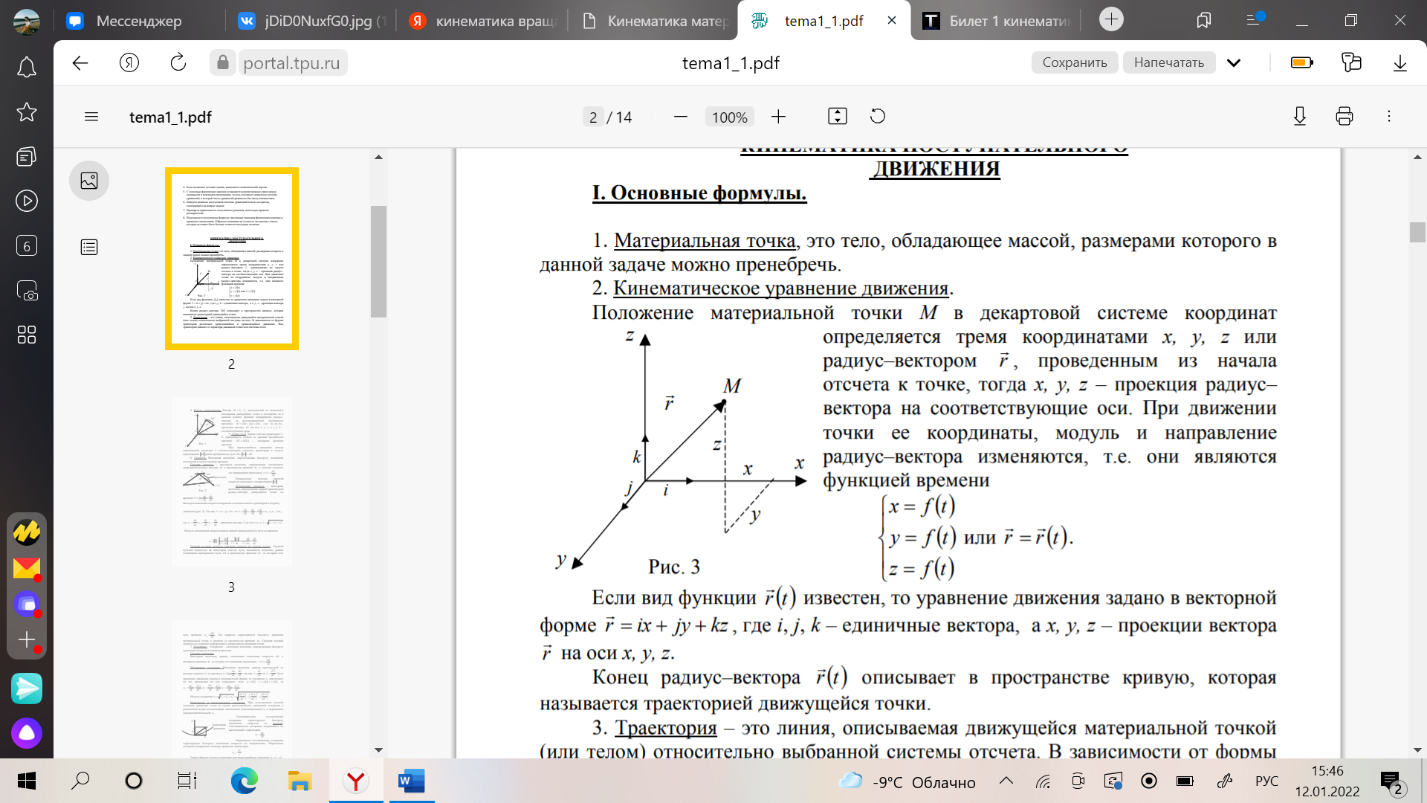 Положение материальной точки М в декартовой системе координат определяется тремя координатами x, y, z или радиус–вектором r r , проведенным из начала отсчета к точке, тогда x, y, z – проекция радиус– вектора на соответствующие оси. При движении точки ее координаты, модуль и направление радиус–вектора изменяются, т.е. они являются функцией времени : 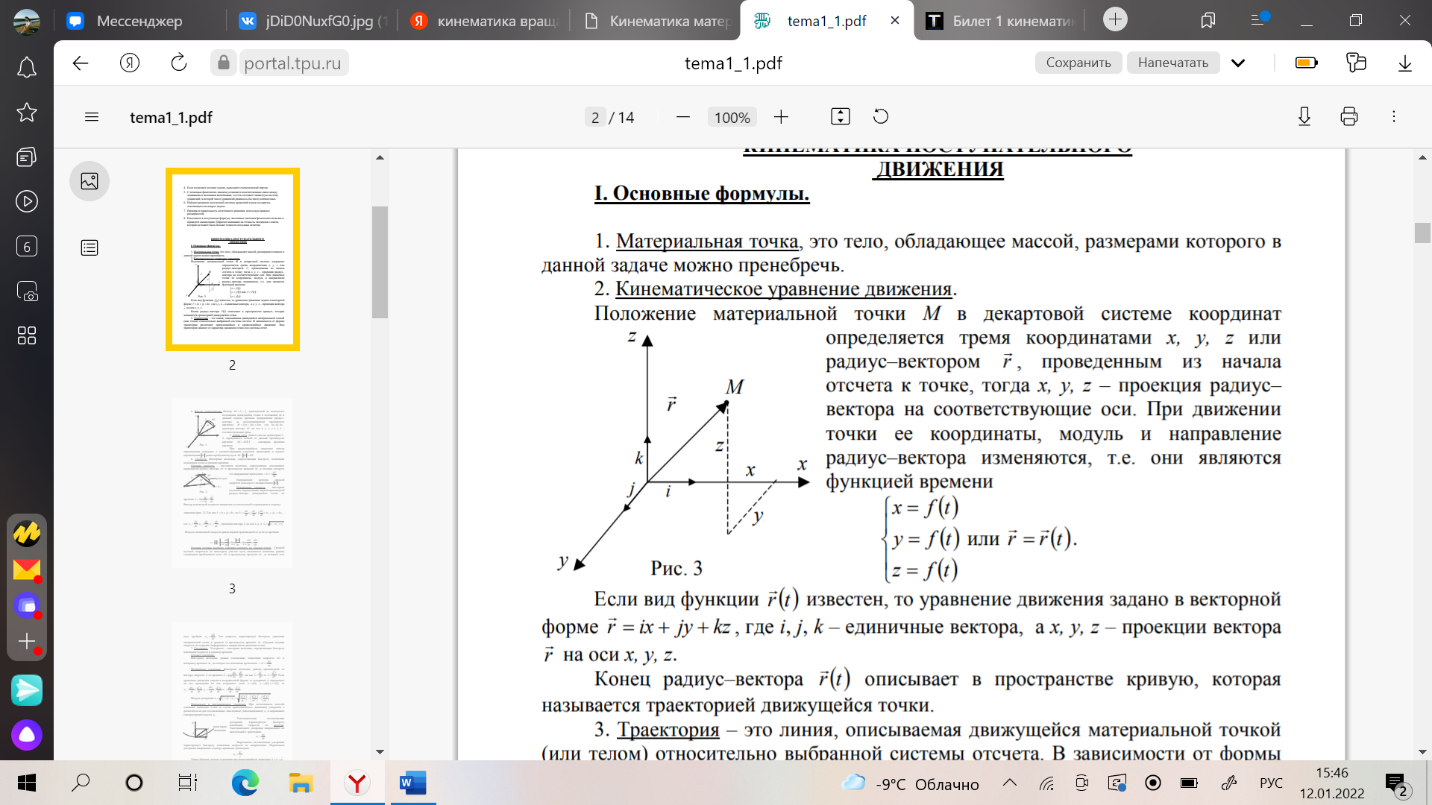 Если вид функции r(t) известен, то уравнение движения задано в векторной форме r = ix + jy + kz , где i, j, k – единичные вектора, а x, y, z – проекции вектора r на оси x, y, z. Конец радиус–вектора r(t) описывает в пространстве кривую, которая называется траекторией движущейся точки. 2. Кинематика вращательного движения материальной точки (угловая скорость, угловое ускорение, тангенсальное ускорение, нормальное ускорение, полное ускорение). Вращательное движение – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой. Вращательное движение материальной точки - движение материальной точки по окружности. Угловая скорость - отношение угла поворота радиус-вектора точки к промежутку времени, за который произошел этот поворот.(направление вдоль оси вокруг которой вращается тело) Угловое ускорение - величина характеризующая изменение вектора угловой скорости со временем. Нормальное и тангенциальное ускорение. При естественном способе описания движения точки (в случае криволинейного движения) ускорение а разлагается на две составляющие: касательное (тангенциальное) τ a и нормальное (центростремительное) n a . Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю. Тангенциальное ускорение направленно по касательной к траектории. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение направлено к центру кривизны траектории. 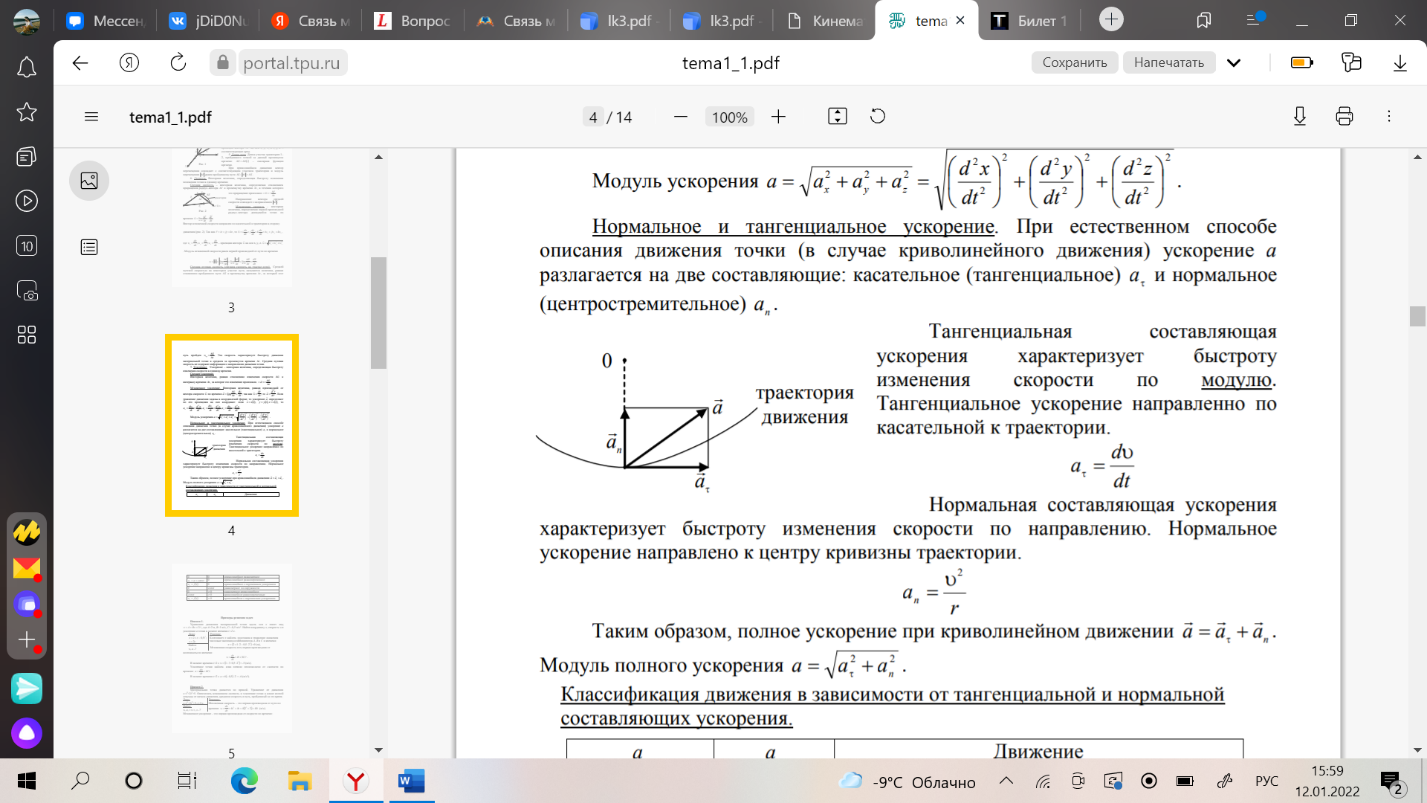 Таким образом, полное ускорение при криволинейном движении Модуль полного ускорения 3. Связь между линейными и угловыми характеристиками движения. 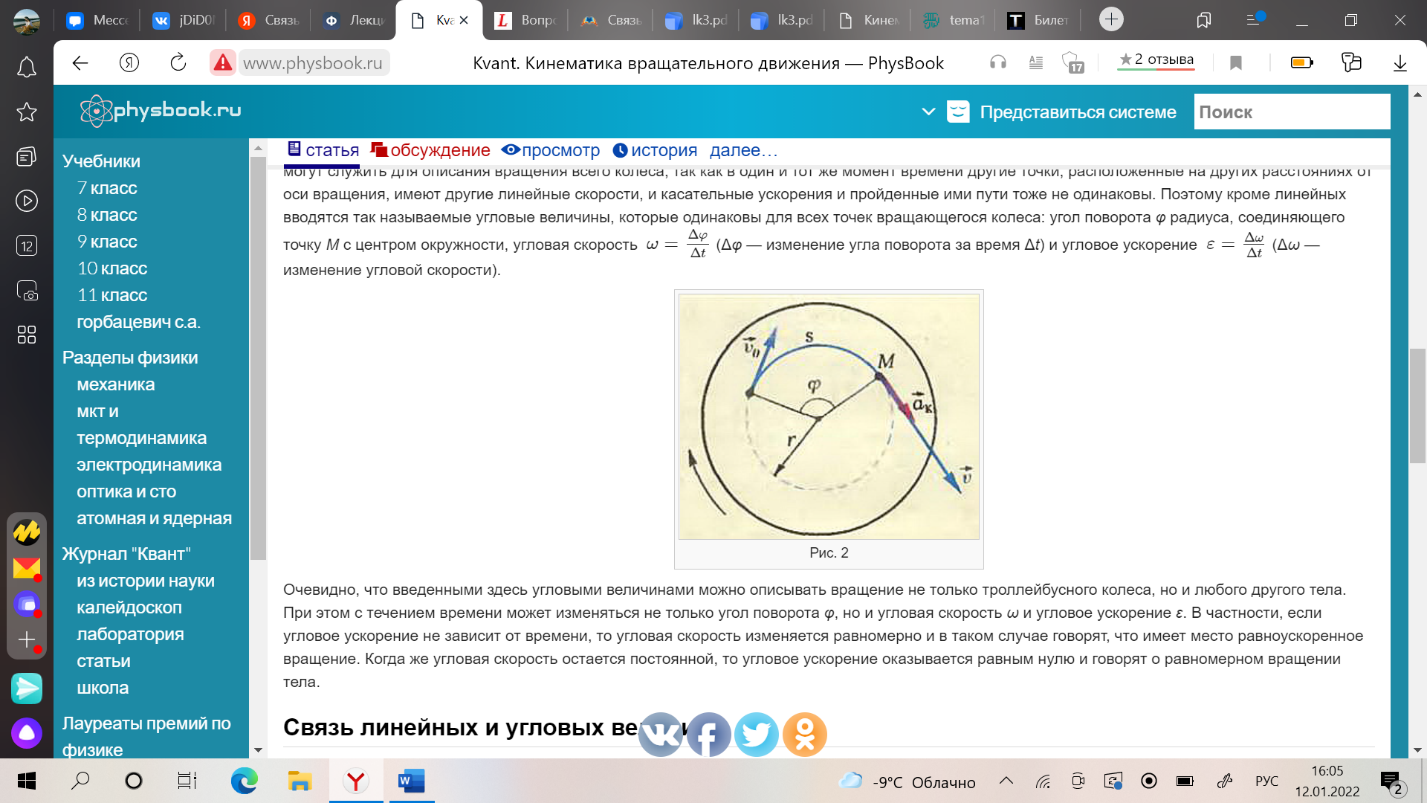 Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи. При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь s=rφ s=rφ . (1) За малое время Δt точка проходит расстояние Δs=rφ2−rφ1, где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что Δs/Δt=υ и φ2−φ1/Δt=Δφ/Δt=ω, получим υ=rω (2) Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть Δυ=rω2−rω1 , где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что Δυ/Δt=ak и ω2−ω1/Δt=Δω/Δt=ε , тогда касательное ускорение ak=rε . (3) Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела. 4. Динамика поступательного движения. Понятие центра инерции (центр масс). Законы ньютона. Поступательное движение- движение, при котором любая прямая проведенная внутри тела, перемещается параллельно самой себе. При поступательно движении все точки тела за одно и то же время совершают одинаковые перемещения и в один и тот же момент времени имеют одинаковые скорости и ускорения. Центр масс (центр инерции) - точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы. 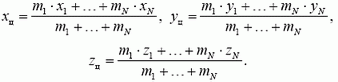 Положение центра масс определяется его радиус-вектором где - радиус-векторы точек, образующих систему. Центр масс замкнутой системы движется прямолинейна и равномерно или остается неподвижным. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции. Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета. Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Ускорение, с которым движется тело, если на него действует сила, прямо пропорционально этой силе и обратно пропорционально массе тела: Сила-это мера воздействия, векторная величина. Масса- мера инертности(состояние покоя). Скалярная величина. Импульс- векторная величина. Количество движений. p = mv -численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости. (1)  Это общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выражение (1) называется также уравнением движения материальной точки. Второй закон Ньютона справедлив только в инерциальных системах отсчета. Инерциа́льная систе́ма отсчёта — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно либо покоятся. Скорость изменения импульса равна действующей на него силе. Принцип суперпозиции. Принцип суперпозиции заключается в замене нескольких сил одной, называемой равнодействующей. 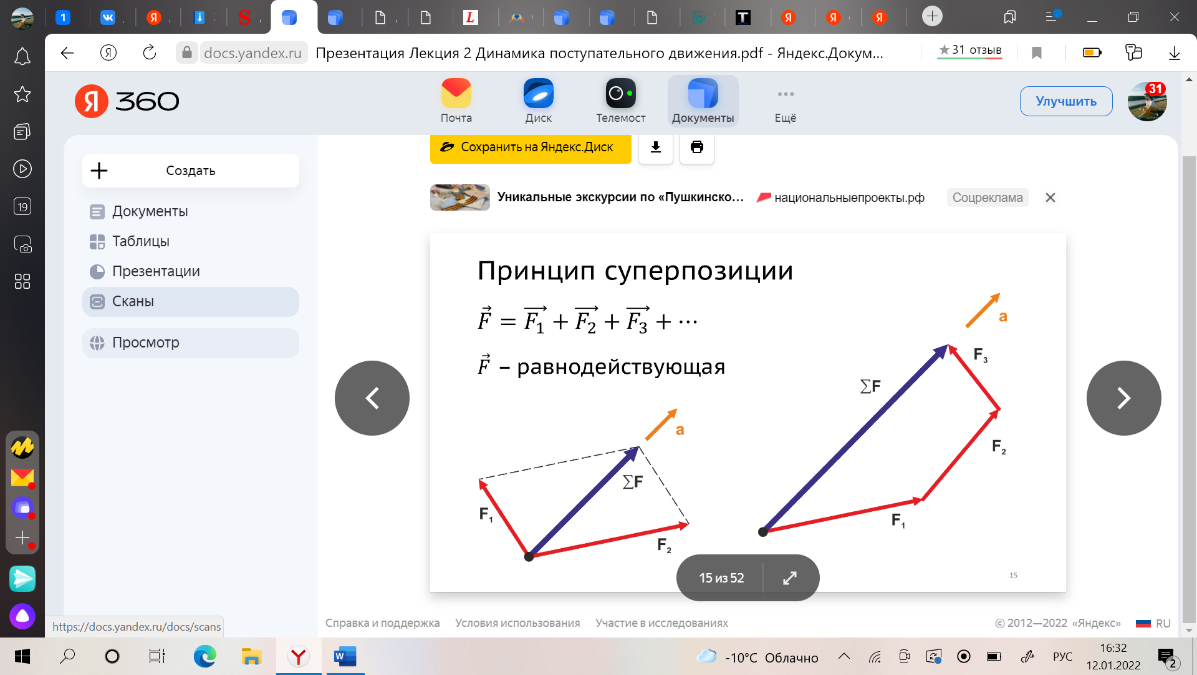 Третий закон Ньютона Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки: Fl2= - F2 1(7.1) где Fl2 — сила, действующая на первую материальную точку со стороны второй; F2 1 — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками. Третий закон Ньютона, как впрочем, и первые два, справедлив только в инерциальных системах отсчета. Принцип относительности Галилея Все законы механики одинаковы во всех инерциальных системах отсчета . Евли в двух системах, одна из которых равномерно и прямолинейно движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым. Находясь в инерциальной система, невозможно определить, покоится она или движется. 5. Понятие об импульсе, моменте импульса, моменте силы. Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. p→=m⋅v→. [p]=1кг⋅м/c. импульс тела — это характеристика движения тела, которая напрямую зависит от его массы и скорости. Чем больше масса и/или скорость движения тела, тем больше его импульс, а значит, тем большее воздействие тело способно оказать на другие тела при взаимодействии с ними. В состоянии покоя скорость равна нулю, следовательно, и величина импульса равна нулю. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его частиц  Таким образом, момент инерции твердого тела относительно оси равен произведению момента инерции на угловую скорость. Момент силы мат. точки относительно некоторого центра-векторная величина, равная векторному произведению радиус-вектора точки, проведенному из полюса в точку приложения силы, на силу . (1) 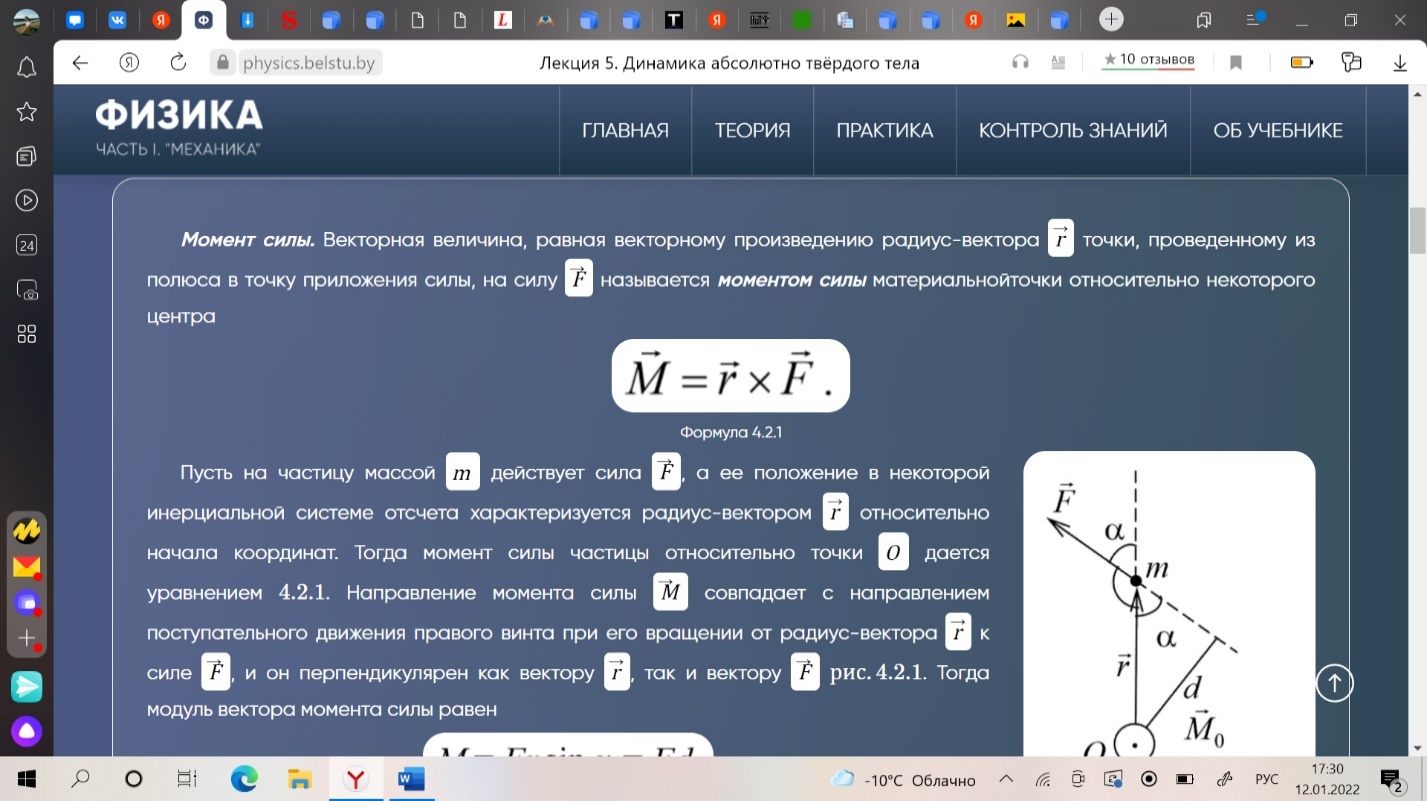 Пусть на частицу массой m действует сила F, а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки О дается уравнением (1). Направление момента силы М совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F, и он перпендикулярен как вектору r, так и вектору F рис. 4.2.1. Тогда модуль вектора момента силы равен. 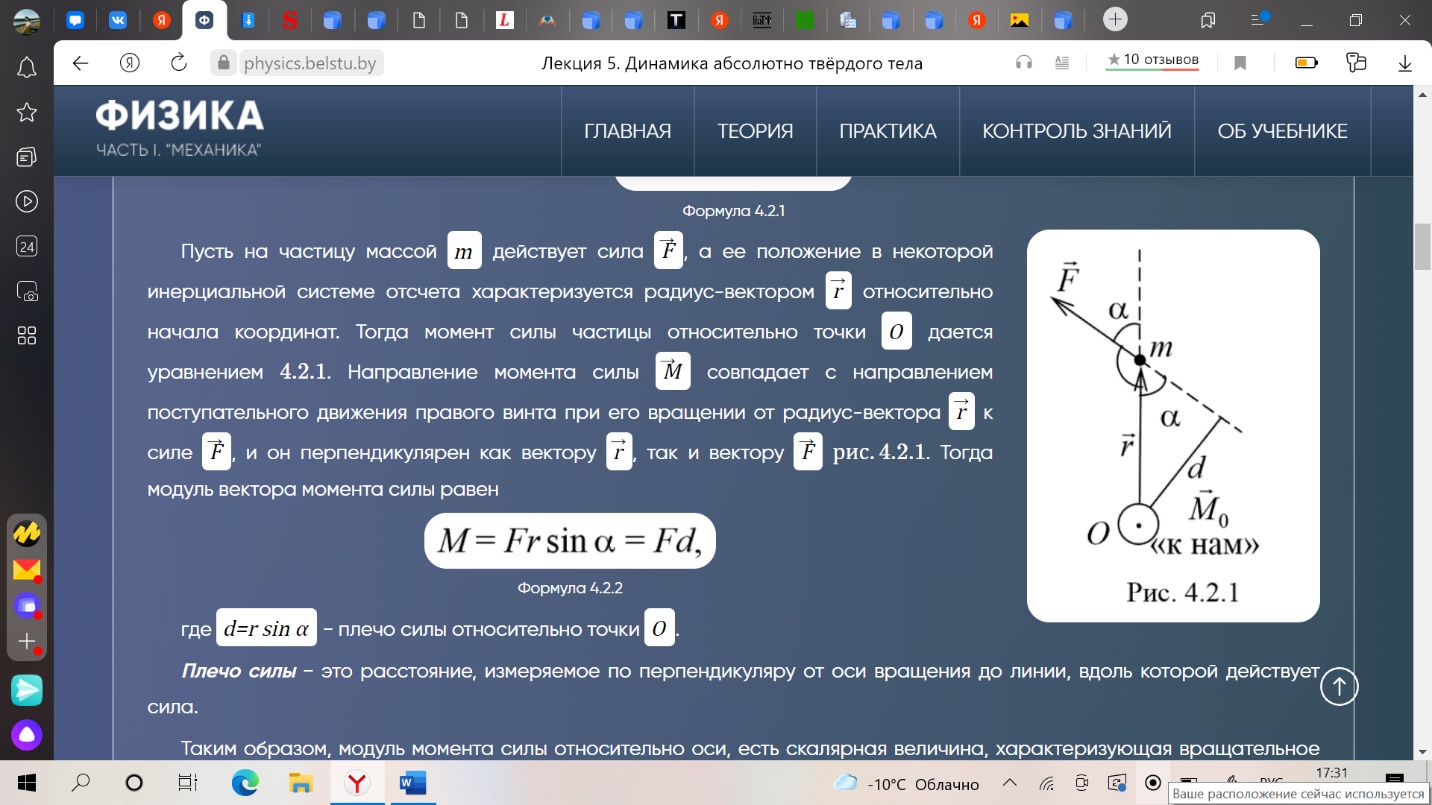 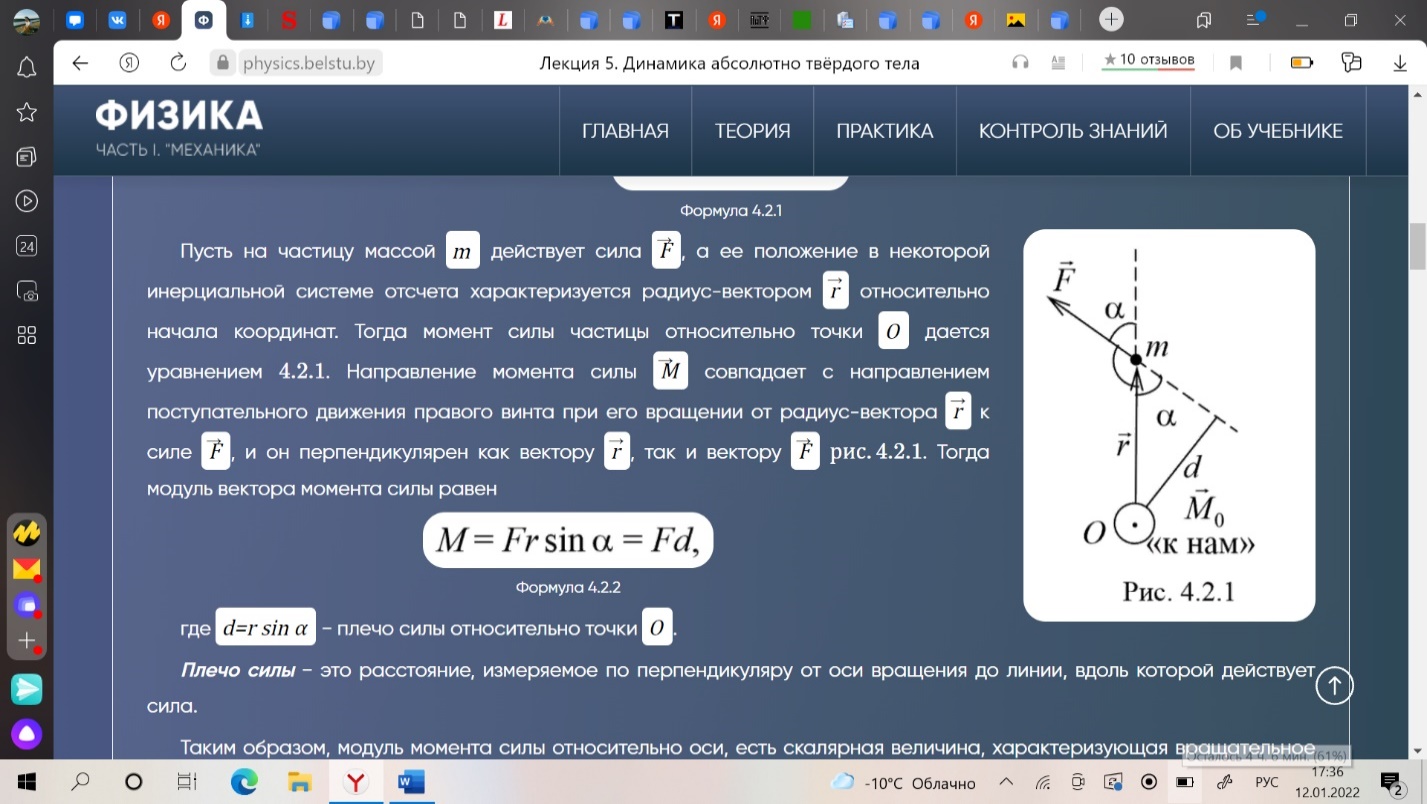 Где d=rsina -плечо силы относительно точки О. Плечо силы- наименьшее расстояние от оси вращения до линии действия силы. Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F, действующей на твердое тело, на плечо силы d относительно этой оси. 6. Момент инерции материальной точки. Момент инерции твердого тела. Теорема Гюйгенса- Штейнера.
В случае непрерывного распределения масс эта сумма сводится к интегралу , где интегрирование производится по объему тела. Главный момент инерции - момент инерции относительно главной оси вращения, проходящей через центр масс. Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему. Моменты инерции однородных тел массой т, имеющих правильную геометрическую форму и равномерное распределение массы по объёму:
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера.
Момент инерции, по определению: Радиус-вектор можно расписать как разность двух векторов:  ,где  — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид: Вынося за сумму , получим: Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:  Тогда:  Откуда и следует искомая формула:  ,где  — известный момент инерции относительно оси, проходящей через центр масс тела.7. Динамика вращательного движения твердого тела. Второй закон Ньютона для вращательного движения. Вывод второго закона Ньютона для вращательного движения Пусть тело, характеристиками которого можно пренебречь закреплено на невесомом стержне, 0 – ось вращения, длиной эквивалентной отрезку r. На материальную точку оказывает воздействие силы , – реакция стержня. — сила реакции нити; — сила приводящая тело в движение r — радиус нити По II закону Ньютона второй закон динамики в векторной форме выглядит: Выбор системы координат: Y – направляется по радиусу, Х – перпендикулярно. Переписывая главное правило динамики в проекциях на эти оси: Для этого на рисунке отобразим угол и выразим через него все проекции. OX: , OY: , Из рисунка видно, что  — тангенциальное ускорение, и  – модуль центростремительного ускоренияВспомним, что тангенциальное ускорение равно: Перепишем уравнение проекции на ось x с учетом этого знания: Вычислим угловое ускорение из полученной формулы: |