1 Классификация игровых моделей. Примеры формализации экономических ситуаций в виде игровых моделей. Игрой теоретикоигровой моделью
 Скачать 45.61 Kb. Скачать 45.61 Kb.
|
  1 Классификация игровых моделей. Примеры формализации экономических ситуаций в виде игровых моделей. Игрой (теоретико-игровой моделью) называется упрощённая формализованная модель конфликтной ситуации, а конфликтующие стороны называются игроками. Ситуация называется конфликтной, если в ней сталкиваются интересы двух или более сторон, преследующих различные (в частном случае противоположные) цели. Однократный розыгрыш игры от начала и до конца называется партией игры. Результатом партии являются платежи (выигрыши или проигрыши игроков). В зависимости от дискретности или непрерывности множества стратегий игры соответственно делятся на дискретные или непрерывные,причем дискретные игры в зависимости от конечности или бесконечности множества стратегий могут быть соответственнои конечными или бесконечными, непрерывные игры – всегда бесконечные. В зависимости от числа участвующих в игре игроков игры бывают N лиц, которые в зависимости от того, разрешены коалиции (кооперации) игроков или нет, могут быть соответственно коалиционными (кооперативными) или некоалиционными (некооперативными), или 2-х лиц (парными), которые в зависимости от суммарной величины платежа могут быть антагонистическими, если суммарный платеж игроков равен нулю, или неантагонистическими, если суммарный платеж не равен нулю. Заметим, что в антагонистической игре интересы игроков строго противоположны, т.е. выигрыш одного игрока в точности равен проигрышу другого, а в неантагонистической – просто не совпадают, что ведет к ситуации, когда увеличение выигрыша одного игрока ведет к уменьшению выигрыша другого. Игра называется игрой с полной информацией, если игрокам известна вся предыстория игры, т.е. все личные и случайные ходы противников (противника), в противном случае имеем игру с неполной информацией. В зависимости от суммарного платежа игроков игры делятся на игры с нулевой суммой, если суммарный платеж равен нулю, и с ненулевой суммой, в противном случае. Примером игры с нулевой суммой является парная антагонистическая игра. И, наконец, в зависимости от числа ходов в партии игры могут быть одноходовые и многоходовые. Наиболее разработанными в теории игр являются модели игр 2-х лиц с нулевой суммой (антагонистических игр). Формализация: Два игрока имеют право загадывать целые числа от 1 до 5, что составляет их соответствующие стратегии. В случае если результат сложения задуманных чисел будет четным, то второй игрок выплачивает первому получившуюся сумму, а если нечетным, то первый – второму. Формализация игры "Красное-чёрное". Есть две команды. Задача каждой команды заработать как можно больше очков. Команда зарабатывает (или теряет) очки, делая выбор: играть на черное или на красное. Мы 1я команда. Система очков: Черное черное (1я -3, 2я -3), черное красное (1я 5, 2я -5), красное черное (1я 3 2я 5), красное красное (-5, 3). 2 Максиминные и минимаксные стратегии. Нижняя и верхняя цены игры в чистых стратегиях. Примеры. Рассмотрим матричную mxn - игру с игроками А и В, в которой игрок А обладает m чистыми стратегиями 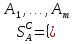 , а игрок В –m чистыми стратегиями , а игрок В –m чистыми стратегиями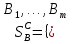 . Значения функции выигрыша игрока А обозначим через . Значения функции выигрыша игрока А обозначим через 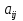 , т. е. , т. е. 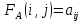 . .Задача состоит в выборе такой стратегии, которая способствует достижению поставленной цели - максимизации выигрыша для игрока А или минимизации проигрыша для игрока В. Перед игроком А стоит задача выбора чистой стратегии из множества 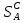 , эффективной в определенном смысле, в результате применения которой он получит максимально возможный гарантированный выигрыш. Если игрок А выбрал стратегию , эффективной в определенном смысле, в результате применения которой он получит максимально возможный гарантированный выигрыш. Если игрок А выбрал стратегию 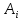 (i=1,…,m), то его выигрышем может быть один из выигрышей (i=1,…,m), то его выигрышем может быть один из выигрышей 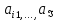 , расположенных в i–й строке матрицы, в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии , расположенных в i–й строке матрицы, в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии 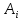 выберет ту стратегию выберет ту стратегию 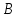 , при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей , при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей 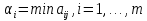 и назовем его показателем эффективности стратегии А,. Продолжая действовать разумно, игрок А должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число 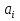 максимально. Если обозначить это максимальное число через максимально. Если обозначить это максимальное число через 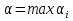 , то , то 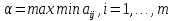 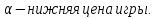 Описанный принцип называется максиминным принципом. Стратегия Описанный принцип называется максиминным принципом. Стратегия 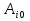 , соответствующая максимину , соответствующая максимину 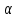 , называется максиминной стратегией игрока А. , называется максиминной стратегией игрока А. Аналогично вводится критерий оценки выигрышей для игрока В. Как игрок В предполагает, что игрок А играет наилучшим для себя образом, то выигрышем игрока А будет максимальное из чисел 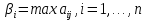 В интересах игрока В - выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел обозначим 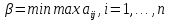 Критерий выбора эффективной стратегии для игрока В называется минимаксным принципом, а выигрыш 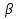 называется минимаксом или верхней ценой игры. Стратегия называется минимаксом или верхней ценой игры. Стратегия 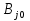 называется минимаксной стратегией игрока В. называется минимаксной стратегией игрока В. нижняя цена игры не больше ее верхней цены в чистых стратегиях: 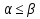 Пример сама 3 Свойство равнозначности седловых точек. Свойство взаимозаменяемости седловых точек. Свойство равнозначности седловых точек матрицы игры Седловые точки обладают важными свойствами. Одно из них – свойство равнозначности. Теорема «свойство равнозначности седловых точек». Если 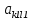 и и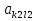 , k1, k2€ , k1, k2€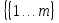 Док-во: Т.к Из неравенств выше, следует неравенство Применив аналогичные рассуждения сначала к седловой точке Свойство взаимозаменяемости седловых точек матрицы игры. Теорема «св-во взаимозаменяемсотиседловых точек» Если Док-во. т.к. с другой стороны по опр. показателя эффективности и показ. неэфф-ти имеем (2): Из равенства (1) и неравенства(2) следует,что а это означает, что Замечание. Теорема сформулирована для случая, когда взаимозаменяются вторые индексы седловых точек Если первые индексы седловых точек |
