анализ данных. 1 Кластерный анализ 4
 Скачать 309.97 Kb. Скачать 309.97 Kb.
|
|
. Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным. В качестве примера проведем дисперсионный анализ для определения влияния средней высоты (Н) на видовое число (f). Исходные данные для расчета показаны в таблице. Исходные данные для дисперсионного анализа влияния средней высоты на видовое число
Здесь изучается влияние средней высоты древостоя на величину среднего видового числа условно одновозрастных спелых ельников. При расчетах на компьютерах суммы 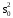 , , 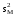 и и 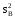 удобнее вычислять по формулам удобнее вычислять по формулам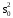 = =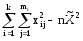 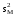 = =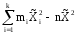 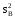 = = 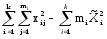 , ,а вместо исходных данных использовать их отклонения от некоторого начального значения, например, от общего среднего 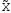 , что упрощает расчеты. Групповые средние приведены в колонке 5. Число групп k=8, общее число наблюдений n = 40. Общее среднее , что упрощает расчеты. Групповые средние приведены в колонке 5. Число групп k=8, общее число наблюдений n = 40. Общее среднее 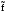 =460. Перейдем к отклонениям от среднего (таблица 6) и вычислим показатели, необходимые для применения формул. =460. Перейдем к отклонениям от среднего (таблица 6) и вычислим показатели, необходимые для применения формул.Из таблицы 18.5 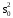 = 36195, = 36195, 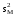 = 14587, = 14587, 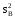 = 36195 - 14587 = 21608. Результаты вычислений запишем в таблицу 6, учитывая, что число степеней свободы для групповой дисперсии paвно k-1=8-1=7, для общей N -1=40-1=39, а для внутригрупповой N -k =40-8=32. = 36195 - 14587 = 21608. Результаты вычислений запишем в таблицу 6, учитывая, что число степеней свободы для групповой дисперсии paвно k-1=8-1=7, для общей N -1=40-1=39, а для внутригрупповой N -k =40-8=32.Вычисление сумм квадратов в однофакторном дисперсионном анализе
Итоги однофакторного дисперсионного анализа
Статистическая характеристика (Fвыч), полученная из, равна Fвыч = 2084/675 =3, 09. При а=0, 05 табличное значение F, взятое из приложения Ж, при ν=7 и N -k=32 будет равно 2, 3. Так как Fвыч > Fтабл., то гипотезу об отсутствии влияния высоты на среднее видовое число древостоя отклоняют: средние 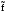 в генеральной совокупности не все равны между собой, а зависят от значения средней высоты. в генеральной совокупности не все равны между собой, а зависят от значения средней высоты.Для расчета методом множественного сравнения предположим, что необходимо выяснить, для каких значений высот можно составить единые таблицы, использующие средние видовые числа. Испытаем, например, возможность объединения высот 22, 24, 26 в одну группу, остальных — во вторую. Функция сравнения по 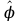 = = 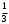 (458, 8+458, 4+467, 6) - (458, 8+458, 4+467, 6) -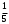 (488, 5+455, 2+472, 8+434, 3+419, 8) = 7, 5 (488, 5+455, 2+472, 8+434, 3+419, 8) = 7, 5а оценка дисперсии по 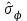 = = 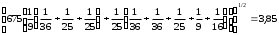 Постоянную s находим из s=[(8-1) F0, 05 (7, 32)]1/2 = (72, 3)1/2 4, т. е. для вероятности 0, 95 имеем доверительный интервал 7, 5 - 4 • 3, 85 7, 5+4 • 3, 85 или —7, 9 22, 9. Так как доверительный интервал содержит ноль, нет оснований объединять материал в указанные группы в зависимости от значении высоты. В данном примере изменена постановка задачи: вместо однофакторного применен двухфакторный анализ (включен дополнительно средний диаметр), после чего удалось удовлетворительным образом сгруппировать материал. Далее используем корреляционное отношение и расчет мощности критерия. Проверим Н0 несколько иначе. Вычислим корреляционное отношение 2, равное отношению межгрупповой дисперсии к сумме квадратов (таблица 7): 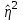 = 14587 / 36195 = 0, 403. Гипотеза Н0: 2 = 0 равносильна Н0: = 14587 / 36195 = 0, 403. Гипотеза Н0: 2 = 0 равносильна Н0: 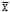 1 = 1 = 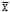 2... = 2... = 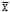 k. Проверим Н0: 2 = 0 при альтернативной На: 2 > 0. Из приложения Т находим критические значения 2 =0, 387 при k1 =7, k2 =32, т.е. гипотезу об отсутствии влияния высоты на видовое число при а =0, 05 отклоняем. k. Проверим Н0: 2 = 0 при альтернативной На: 2 > 0. Из приложения Т находим критические значения 2 =0, 387 при k1 =7, k2 =32, т.е. гипотезу об отсутствии влияния высоты на видовое число при а =0, 05 отклоняем.4 КОЭФФИЦИЕНТ РЕГРЕССИИ: СТАТИСТИЧЕСКОЕ ЗНАЧЕНИЕ Коэффициент регрессии показывает, насколько в среднем величина одного признака y изменяется при изменении на единицу меры другого, корреляционно связанного с Y признака X. Этот показатель определяют по формуле 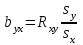 или или 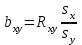 . . Здесь значения s умножают на размеры классовых интервалов λ, если их находили по вариационным рядам или корреляционным таблицам. Коэффициент регрессии можно вычислить минуя расчет средних квадратичных отклонений sy и sx по формуле 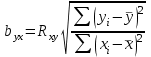 или или 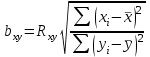 . . Если же коэффициент корреляции неизвестен, коэффициент регрессии определяют следующим образом: 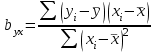 или или 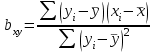 . . Для расчета коэффициента регрессии возьмем данные задачи пункта 2. Из табличных данных и промежуточных расчетов, проведенных в пункте 2, следует, что Выборочные дисперсии: Следовательно, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: Значимость коэффициента корреляции. Выдвигаем гипотезы: H0: rxy = 0, нет линейной взаимосвязи между переменными; H1: rxy ≠ 0, есть линейная взаимосвязь между переменными; Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 ≠ 0, надо вычислить наблюдаемое значение критерия (величина случайной ошибки) 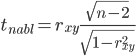 и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы k = n - 2 найти критическую точку tкритдвусторонней критической области. Если tнабл < tкрит оснований отвергнуть нулевую гипотезу. Если |tнабл| > tкрит — нулевую гипотезу отвергают. 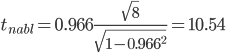 По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=8 находим tкрит: tкрит (n-m-1;α/2) = (8;0.025) = 2.306 где m = 1 - количество объясняющих переменных. Если |tнабл| > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). Поскольку |tнабл| > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Гашев С. Н. Математические методы в биологии: анализ биологических данных в системе Statistica. — М.: Юрайт. 2020. 208 с. Козлов А.Ю. Статистический анализ данных в MS Excel: Учебное пособие / А.Ю. Козлов, В.С. Мхитарян, В.Ф. Шишов. — М.: Инфра-М, 2018. — 80 c. Кравченко А. И. Анализ и обработка социологических данных. Учебник. — М.: КноРус. 2020. 498 с. Кулаичев А.П. Методы и средства комплексного анализа данных: Учебное пособие / А.П. Кулаичев. — М.: Форум, 2018. — 160 c. Миркин Б. Г. Введение в анализ данных. — М.: Юрайт. 2020. 175 с. Мхитарян В. С. Теория планирования эксперимента и анализ статистических данных. — М.: Юрайт. 2020. 491 с. Нархид Н. Apache Kafka. Потоковая обработка и анализ данных / Н. Нархид. — СПб.: Питер, 2019. — 320 c. Ниворожкина Л.И. Статистические методы анализа данных: Учебник / Л.И. Ниворожкина, С.В. Арженовский, А.А. Рудяга. — М.: Риор, 2018. — 320 c. Панкратова Е.В. Анализ данных в программе SPSS для начинающих социологов / Е.В. Панкратова, И.Н. Смирнова, Н.Н. Мартынова. — М.: Ленанд, 2018. — 200 c. Рафалович В. Data mining, или интеллектуальный анализ данных для занятых. Практический курс / В. Рафалович. — М.: SmartBook, 2018. — 352 c. Салин В. Н., Чурилова Э. Ю. Статистический анализ данных цифровой экономики в системе "Statistica". Учебно-практическое пособие. — М.: КноРус. 2019. 240 с. Сидняев Н. И. Теория планирования эксперимента и анализ статистических данных. — М.: Юрайт. 2020. 496 с. Симчера В.М. Методы многомерного анализа статистических данных / В.М. Симчера. — М.: Финансы и статистика, 2018. — 400 c. Тюрин Ю.Н. Анализ данных на компьютере: Учебное пособие / Ю.Н. Тюрин, А.А. Макаров; Науч. ред. В.Э. Фигурнов. — М.: ИД ФОРУМ, 2017. — 368 c. |