анализ данных. 1 Кластерный анализ 4
 Скачать 309.97 Kb. Скачать 309.97 Kb.
|
|
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №2,7,9 и №5. В результате имеем 7 кластера: S(1), S(2,7,9,5), S(3), S(4), S(6), S(8), S(10) Из матрицы расстояний следует, что объекты 1 и 10 наиболее близки P1;10 = 2 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1 и №10. В результате имеем 6 кластера: S(1,10), S(2,7,9,5), S(3), S(4), S(6), S(8) Из матрицы расстояний следует, что объекты 1,10 и 4 наиболее близки P1,10;4 = 2 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,10 и №4. В результате имеем 5 кластера: S(1,10,4), S(2,7,9,5), S(3), S(6), S(8) Из матрицы расстояний следует, что объекты 2,7,9,5 и 6 наиболее близки P2,7,9,5;6 = 2 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №2,7,9,5 и №6. В результате имеем 4 кластера: S(1,10,4), S(2,7,9,5,6), S(3), S(8) Из матрицы расстояний следует, что объекты 1,10,4 и 2,7,9,5,6 наиболее близки P1,10,4;2,7,9,5,6 = 3.16 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,10,4 и №2,7,9,5,6. В результате имеем 3 кластера: S(1,10,4,2,7,9,5,6), S(3), S(8) Из матрицы расстояний следует, что объекты 1,10,4,2,7,9,5,6 и 3 наиболее близки P1,10,4,2,7,9,5,6;3 = 3.61 и поэтому объединяются в один кластер.
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,10,4,2,7,9,5,6 и №3. В результате имеем 2 кластера: S(1,10,4,2,7,9,5,6,3), S(8)
Вывод: при проведении кластерного анализа по принципу “ближнего соседа” получили два кластера, расстояние между которыми равно P=5. 2 РЕГРЕССИОННЫЙ АНАЛИЗ СО СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТЬЮ В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) диаграмму рассеяния математическим уравнением. То есть зависимость между переменными величинами Y и Х можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. График корреляционной зависимости строится по уравнениям функции Для выражения регрессии служат эмпирические и теоретические ряды, их графики — линии регрессии, а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии. Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины Ряды регрессии, особенно их графики, дают наглядное представление о форме и тесноте корреляционной связи между признаками, в чем и заключается их ценность. Форма связи между показателями, влияющими на уровень спортивного результата и общей физической подготовки занимающихся физической культурой и спортом, может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами Y и X, предвидеть возможные изменения признака Y на основе известных изменений X, связанного с Y корреляционно. Первая строка - цена реализации 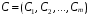 , а вторая строка , а вторая строка 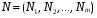 – соответствующий объем реализации. – соответствующий объем реализации. 4.64 5.63 3.65 3.35 3.77 4.90 5.49 6.14 4.19 4.03 7.33 6.46 8.63 8.64 8.19 7.21 6.39 6.04 8.26 8.76 Для удобства обозначим цену реализации переменной Х, объем реализации переменной У На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид y = bx + a Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти. Здесь ε - случайная ошибка (отклонение, возмущение). Точечный график: 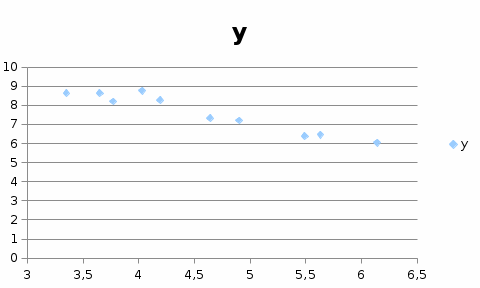 Из рисунка видно, что между переменными существует линейная обратная зависимость. Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x). Формально критерий МНК можно записать так: S = ∑(yi - y*i)2 → min Система нормальных уравнений. a•n + b∑x = ∑y a∑x + b∑x2 = ∑y•x Для расчета параметров регрессии построим расчетную таблицу.
Для наших данных система уравнений имеет вид 10a + 45.79 b = 75.91 45.79 a + 217.63 b = 339.11 Домножим уравнение (1) системы на (-4.58), получим систему, которую решим методом алгебраического сложения. -45.79a -209.72 b = -347.67 45.79 a + 217.63 b = 339.11 Получаем: 7.91 b = -8.56 Откуда b = -1.0659 Теперь найдем коэффициент «a» из уравнения (1): 10a + 45.79 b = 75.91 10a + 45.79 • (-1.0659) = 75.91 10a = 124.72 a = 12.4718 Получаем эмпирические коэффициенты регрессии: b = -1.0659, a = 12.4718 Уравнение регрессии (эмпирическое уравнение регрессии): y = -1.0659 x + 12.4718 Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: Коэффициент корреляции Ковариация. Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rxy < 0.3: слабая; 0.3 < rxy < 0.5: умеренная; 0.5 < rxy < 0.7: заметная; 0.7 < rxy < 0.9: высокая; 0.9 < rxy < 1: весьма высокая; В нашем примере связь между признаком Y фактором X весьма высокая и обратная. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: В парной линейной регрессии t2r = t2b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии. Интервальная оценка для коэффициента корреляции (доверительный интервал). Доверительный интервал для коэффициента корреляции. r(-1;-0.755) Уравнение регрессии (оценка уравнения регрессии). Линейное уравнение регрессии имеет вид y = -1.07 x + 12.47 Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент регрессии b = -1.07 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y понижается в среднем на -1.07. Коэффициент a = 12.47 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь обратная. Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических: Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. В среднем, расчетные значения отклоняются от фактических на 2.54%. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии. Для линейной регрессии индекс корреляции равен коэффициенту корреляции rxy = -0.966. Полученная величина свидетельствует о том, что фактор x существенно влияет на y Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции: 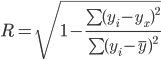 Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции rxy. В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1]. Теоретическое корреляционное отношение для линейной связи равно коэффициенту корреляции rxy. Коэффициент детерминации. Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака. Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. R2= -0.9662 = 0.9328 т.е. в 93.28% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 6.72% изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации). Для оценки качества параметров регрессии построим расчетную таблицу.
Оценка параметров уравнения регрессии. Анализ точности определения оценок коэффициентов регрессии. Несмещенной оценкой дисперсии возмущений является величина: S2 = 0.0814 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). S = 0.29 - стандартная ошибка оценки (стандартная ошибка регрессии). Sa - стандартное отклонение случайной величины a. 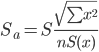 Sb - стандартное отклонение случайной величины b. Доверительные интервалы для зависимой переменной. Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения. Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов. Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и Xp = 5.35 tкрит (n-m-1;α/2) = (8;0.025) = 2.306 y(5.35) = -1.066*5.35 + 12.472 = 6.769 Вычислим ошибку прогноза для уравнения y = bx + a 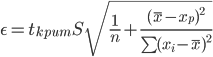 Или 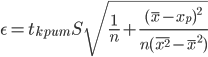 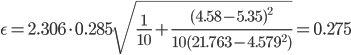 6.769 ± 0.275 (6.49;7.04) С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов. Вычислим ошибку прогноза для уравнения y = bx + a + ε 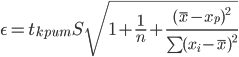 (6.06;7.48) Индивидуальные доверительные интервалы для Y при данном значении X. (a + bxi ± ε) где 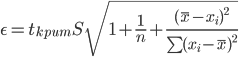 tкрит (n-m-1;α/2) = (8;0.025) = 2.306
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов. Проверка гипотез относительно коэффициентов линейного уравнения регрессии. t-статистика. Критерий Стьюдента. С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y). Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Чтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез. В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности. Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05. H0: b = 0, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности; H1: b ≠ 0, то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности. В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента. Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение определяется в зависимости от уровня значимости (α) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений. Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-α) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля. Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости α. tкрит (n-m-1;α/2) = (8;0.025) = 2.306 Поскольку 10.54 > 2.306, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента). Поскольку 26.44 > 2.306, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента). Доверительный интервал для коэффициентов уравнения регрессии. Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими: (b - tкрит Sb; b + tкрит Sb) (-1.07 - 2.306 • 0.1; -1.07 + 2.306 • 0.1) (-1.299;-0.833) С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале. (a - tкрит Sa; a + tкрит Sa) (12.472 - 2.306 • 0.47; 12.472 + 2.306 • 0.47) (11.384;13.56) С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале. 2) F-статистика. Критерий Фишера. Коэффициент детерминации R2 используется для проверки существенности уравнения линейной регрессии в целом. Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. 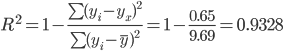 где m – число факторов в модели. Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α. 2. Далее определяют фактическое значение F-критерия: где m=1 для парной регрессии. 3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2. Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01. 4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом. Табличное значение критерия со степенями свободы k1=1 и k2=8, Fтабл = 5.32 Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством: 3 ДИСПЕРСИОННЫЙ АНАЛИЗ Дисперсионный анализ применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную (отклик). Дисперсионный анализ, предложенный Р. Фишером, является статистическим методом, предназначенным для выявления влияния ряда отдельных факторов на результаты экспериментов. В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные), а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат. Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F — критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов. Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок, которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие) |
