|
|
информатика. Глава 1, часть 2_р. 1 Кодирование текстовых и символьных данных
Первичным понятием теории множеств является понятие самого множества. Множество — это совокупность некоторых (произвольных) объектов, объединенных по какому-либо признаку. Элементы множества при этом должны быть различными. Множество обозначается парой скобок 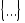 , внутри которых либо просто перечисляются элементы, либо описываются их свойства. Например, , внутри которых либо просто перечисляются элементы, либо описываются их свойства. Например, 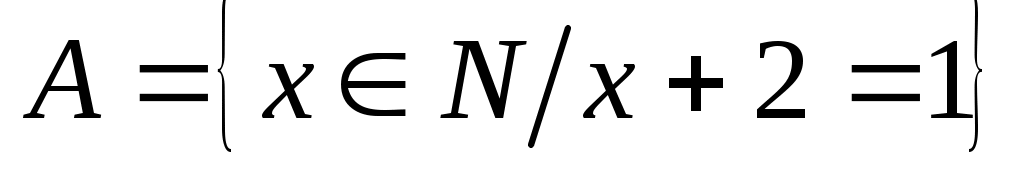 — множество натуральных чисел, удовлетворяющих условию — множество натуральных чисел, удовлетворяющих условию 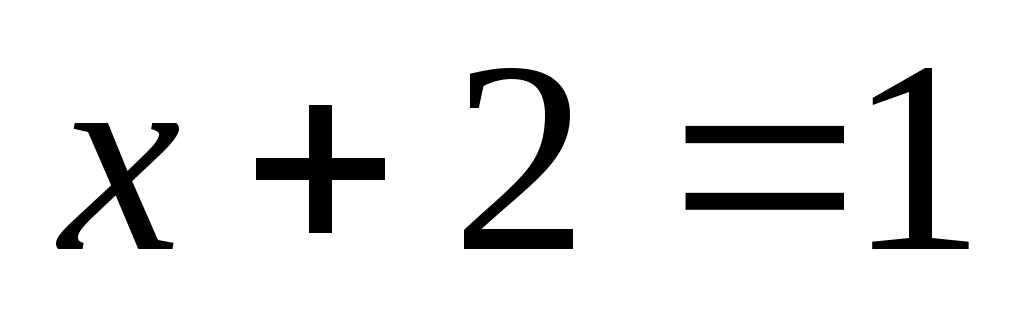 , очевидно, пусто. , очевидно, пусто.  сложение, умножение сложение, умножение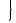 — множество основных арифметических операций. Пустое множество обозначается знаком . Если необходимо указать, что объект — множество основных арифметических операций. Пустое множество обозначается знаком . Если необходимо указать, что объект  является элементом множества является элементом множества  , то пишут , то пишут  ( ( принадлежит принадлежит  ), наоборот запись ), наоборот запись 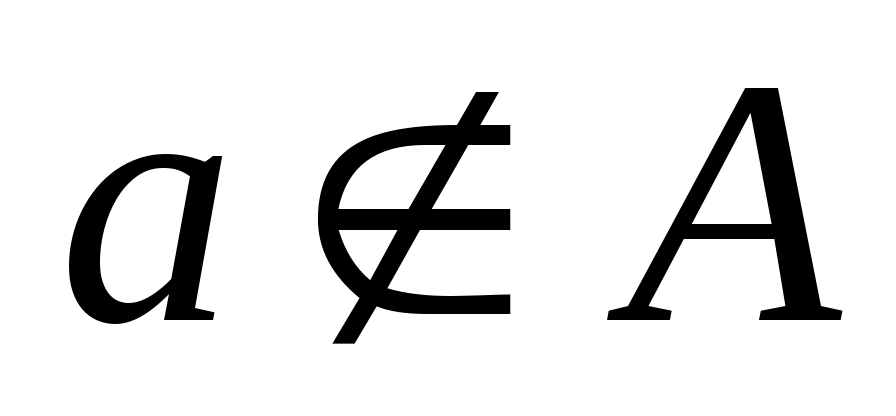 говорит о том, что говорит о том, что  не принадлежит не принадлежит 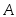 . .
Если каждый элемент множества 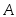 является элементом множества является элементом множества 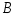 , то пишут , то пишут 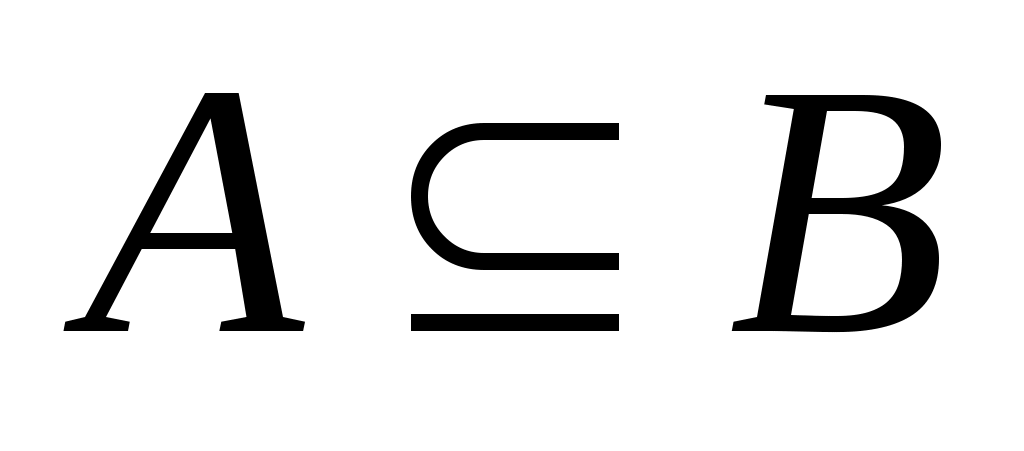 или или 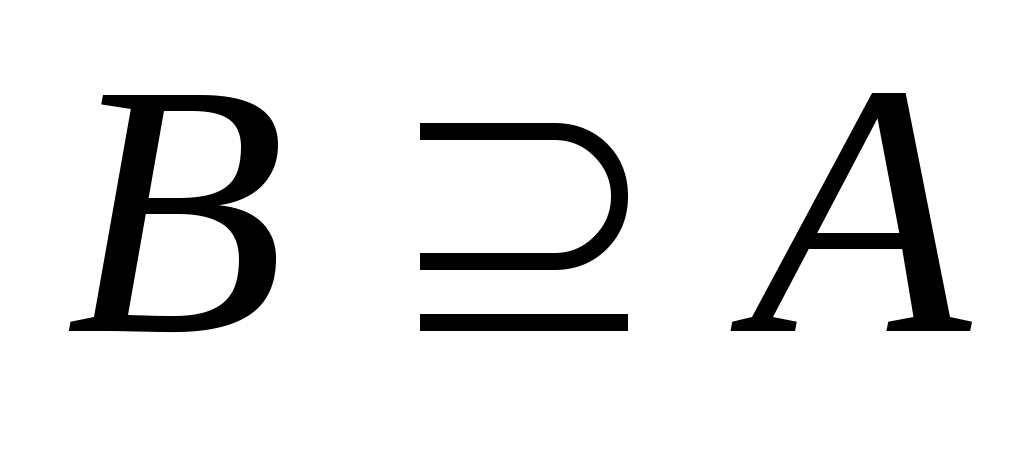 и говорят, что множество и говорят, что множество 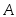 является подмножеством множества является подмножеством множества 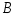 . Если . Если  есть подмножество множества есть подмножество множества 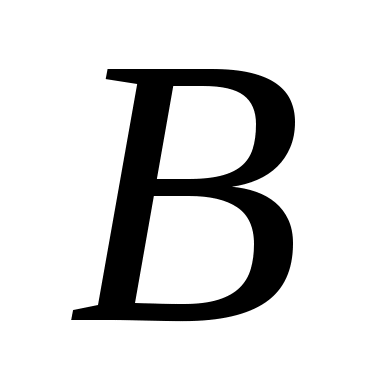 , причем , причем 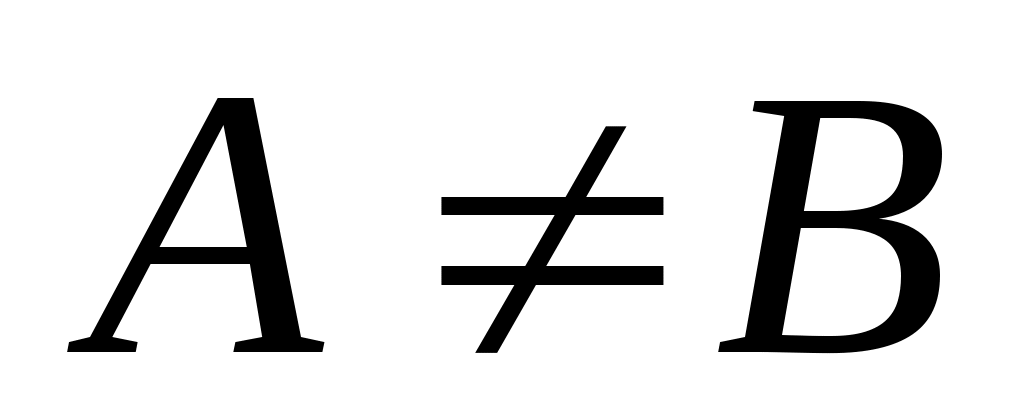 , то пишут , то пишут  или или 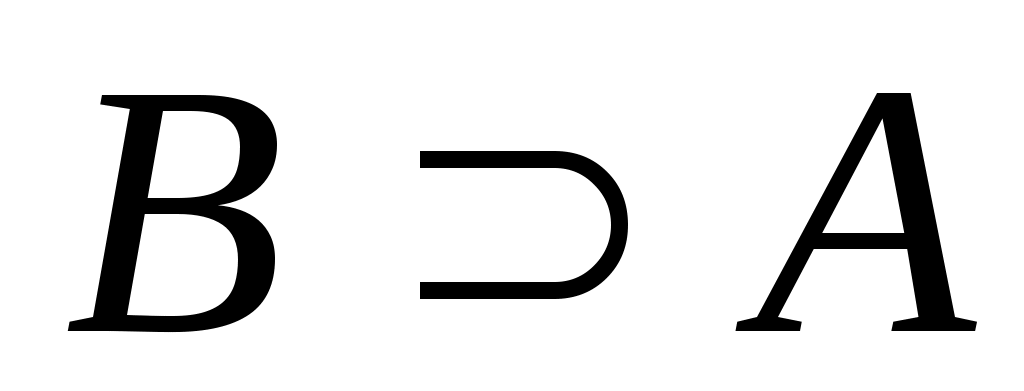 . Множества, состоящие из одних и тех же элементов, называются равными, то есть . Множества, состоящие из одних и тех же элементов, называются равными, то есть 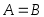 , в противном случае , в противном случае 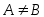 . С помощью скобок и операций над множествами можно построить новые множества, более сложные, чем исходные. . С помощью скобок и операций над множествами можно построить новые множества, более сложные, чем исходные.
Объединение (или сумма). Эта операция над множествами обозначается 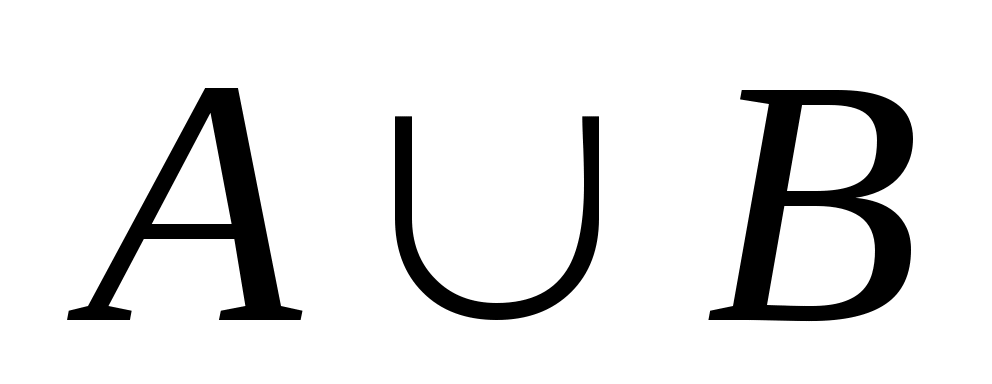 , определяется как , определяется как 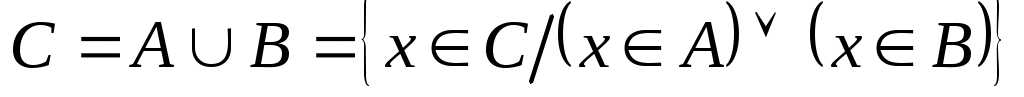 . Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера5- Венна6. Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить . Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера5- Венна6. Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить 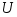 (или (или 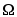 ) и изобразить его в виде всей плоскости, то любое множество ) и изобразить его в виде всей плоскости, то любое множество 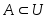 можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество 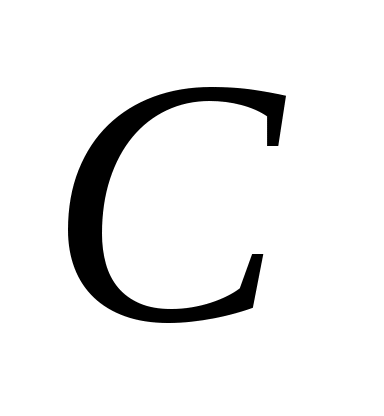 объединение множеств объединение множеств  и и  , , 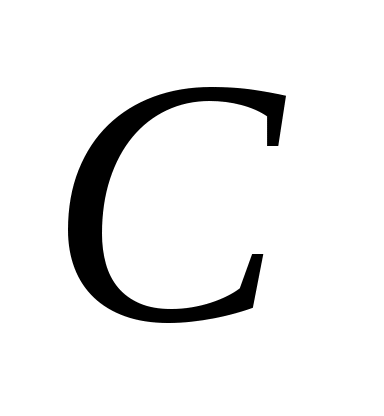 на рис. 1.7 заштриховано. на рис. 1.7 заштриховано. 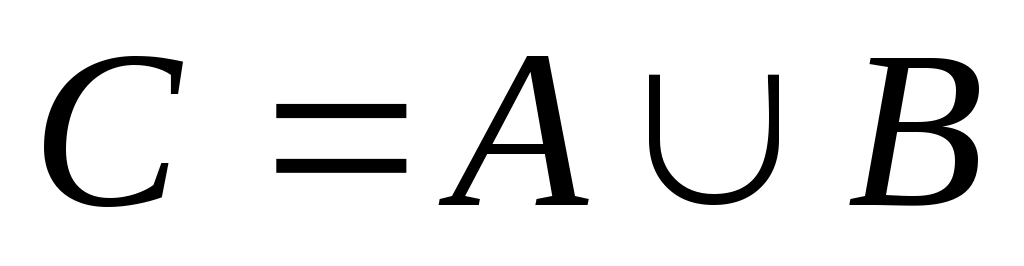 . .
Р
ис. 1.7. Объединение множеств
Рис. 1.8. Пересечение множеств
Пересечением (или произведением) двух множеств называется такое множество 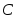 , которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть , которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть 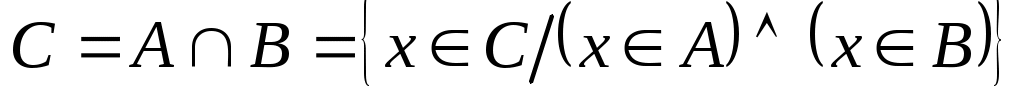 . Пересечение множеств . Пересечение множеств 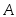 и и 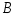 заштриховано и изображено на рис. 1.8. заштриховано и изображено на рис. 1.8.
Разностью двух множеств 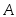 и и 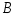 называется множество называется множество 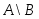 , состоящее из тех и только тех элементов, которые входят в , состоящее из тех и только тех элементов, которые входят в 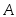 и одновременно не входят в и одновременно не входят в 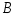 , то есть , то есть 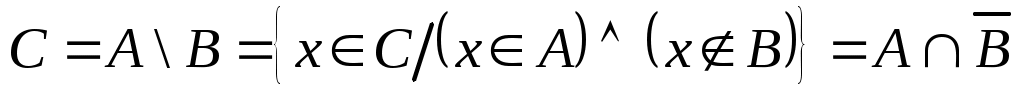 (рис. 1.9). Если, в частности, (рис. 1.9). Если, в частности,  подмножество подмножество  , то разность , то разность 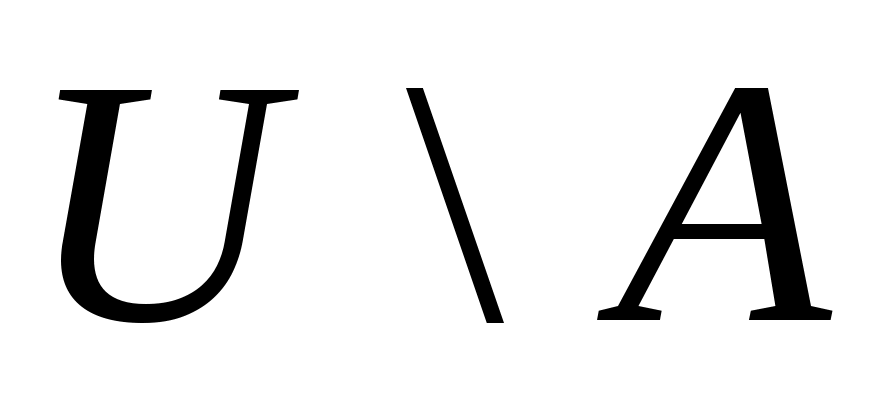 обозначается обозначается 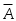 и называется дополнением множества и называется дополнением множества 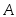 (рис. 1.10). (рис. 1.10).
Рис. 1.9. Разность множеств
Рис. 1.10. Дополнение множества
С
имметрической разностью или кольцевой суммой множеств  и и 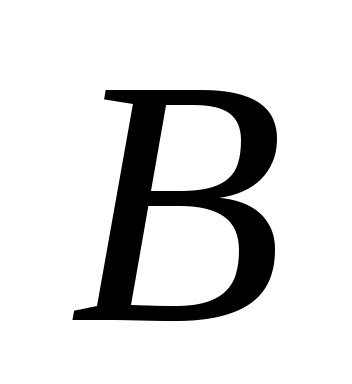 называется множество называется множество 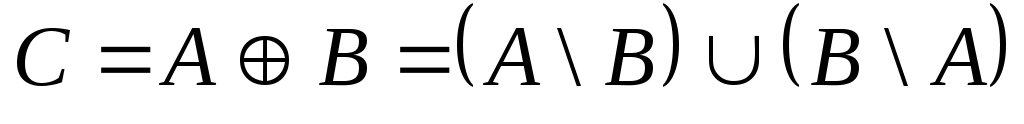 (рис. 1.11). Очевидно, что (рис. 1.11). Очевидно, что 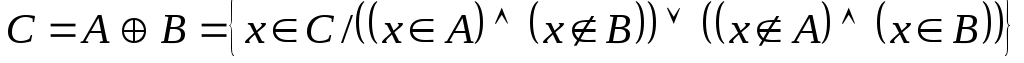 . Если . Если  и и 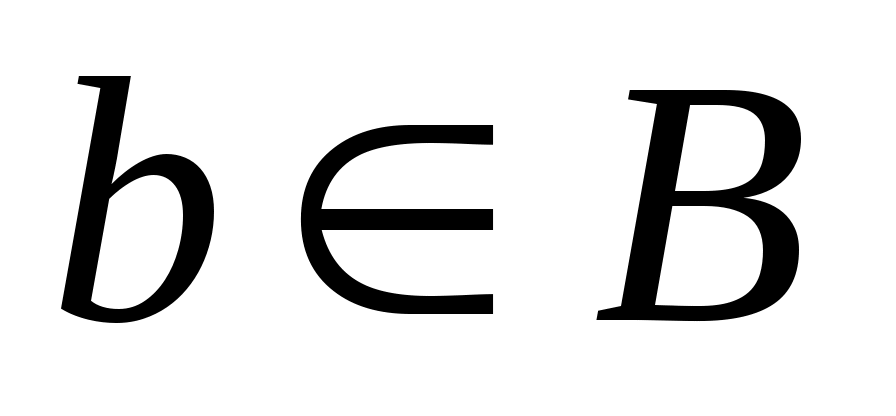 , то пару элементов , то пару элементов 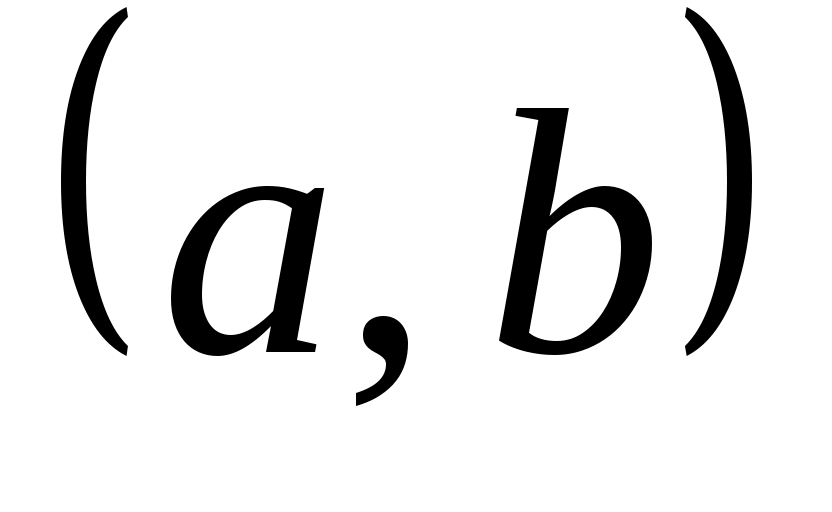 называют упорядоченной парой, причем пары называют упорядоченной парой, причем пары 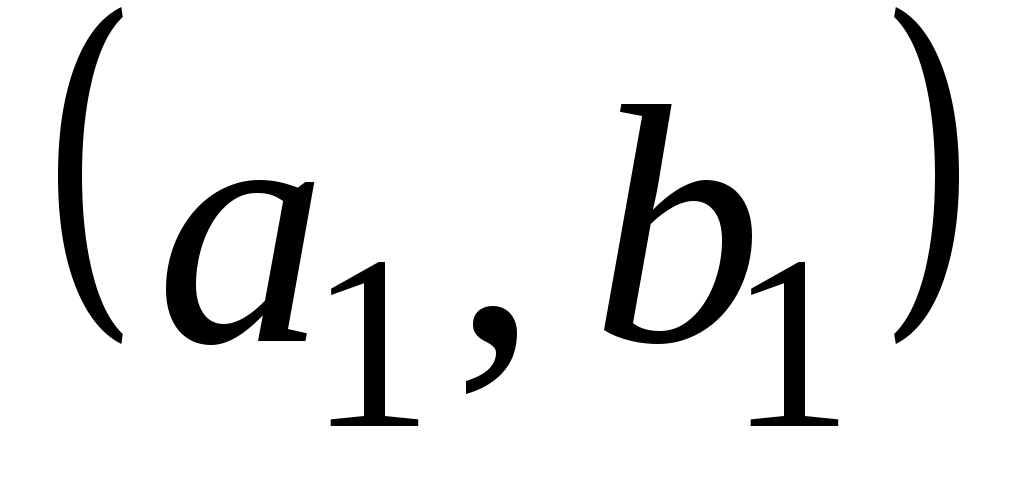 и и 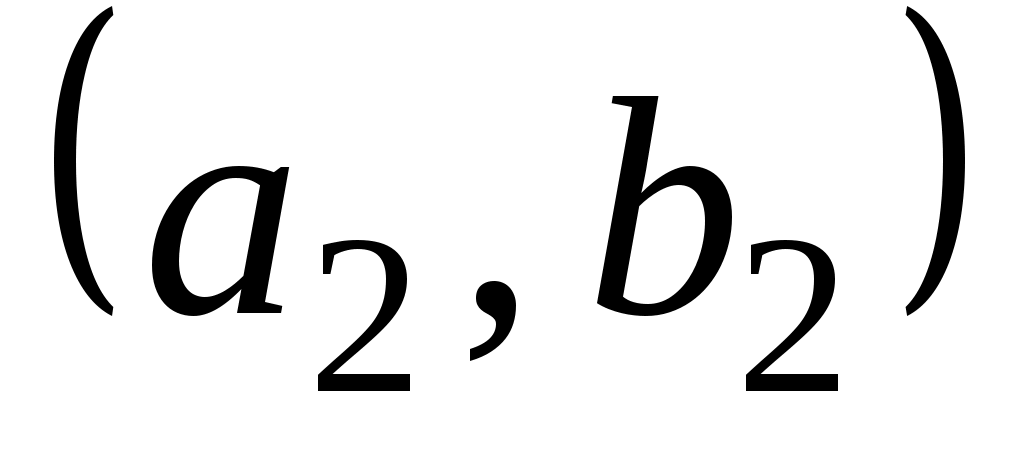 равны тогда и только тогда, когда равны тогда и только тогда, когда 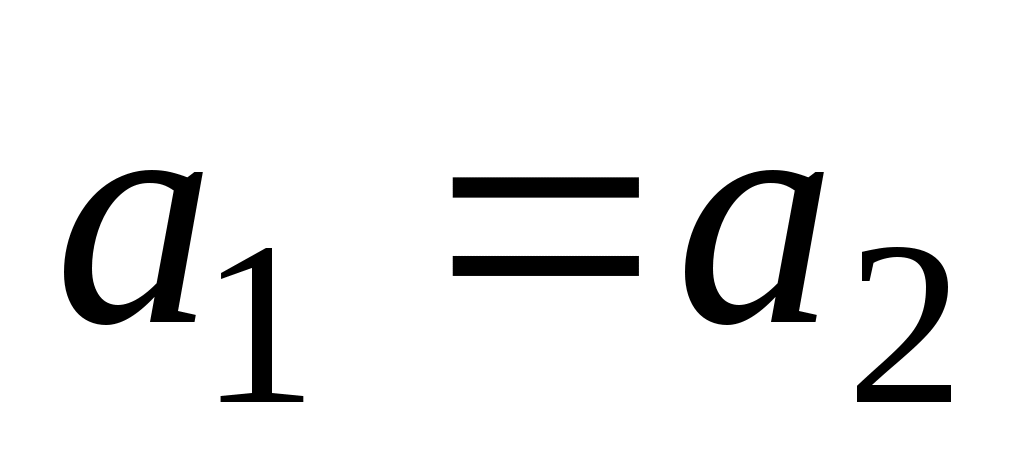 и и 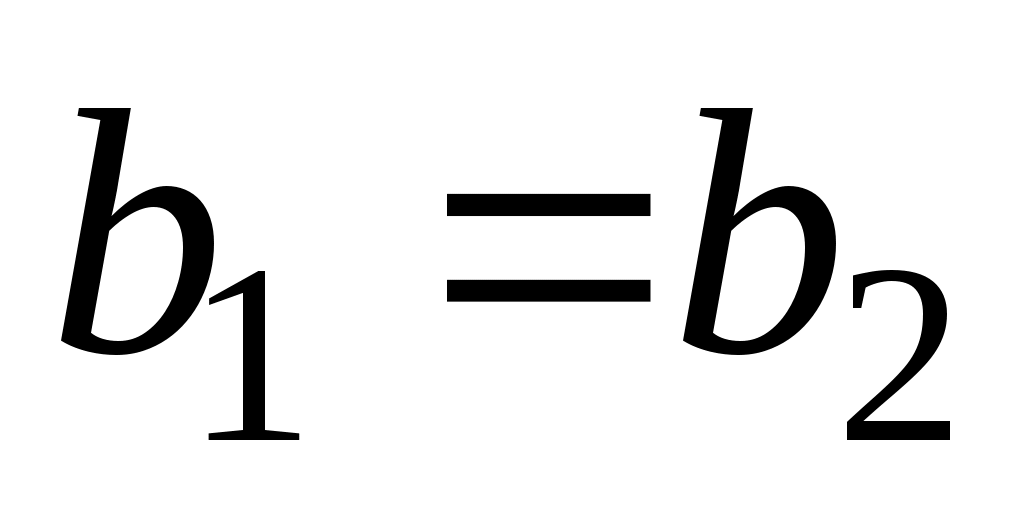 . .
Р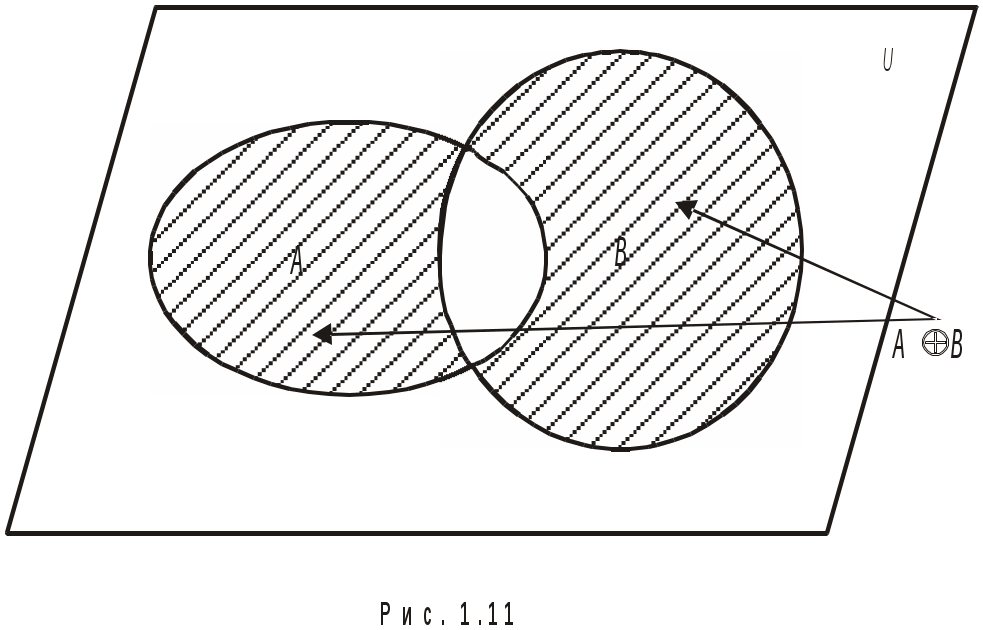
ис. 1.11. Симметрическая разность
Множество, элементами которого являются все упорядоченные пары 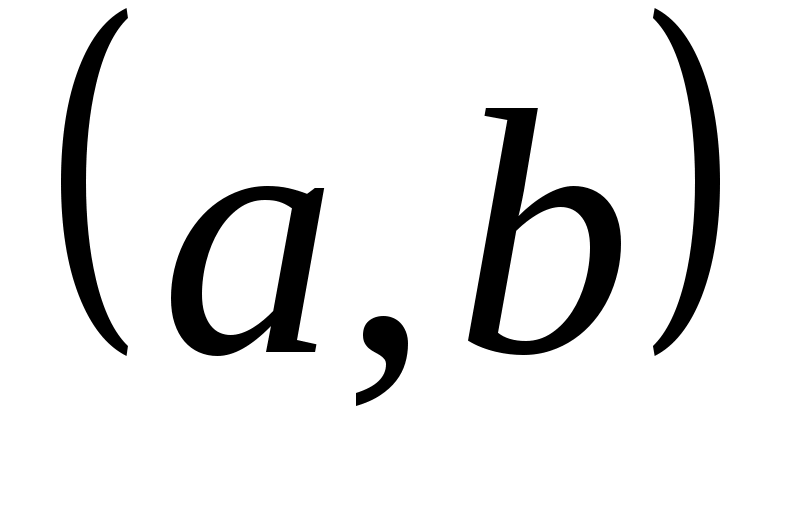 , ,  , , 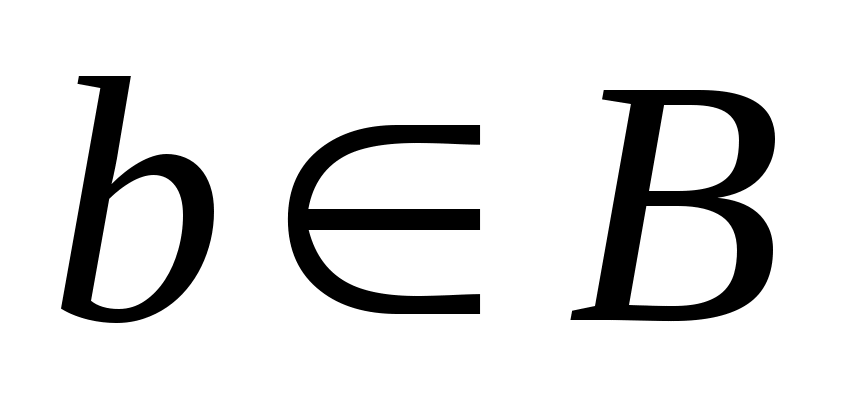 называется прямым или декартовым произведением множеств называется прямым или декартовым произведением множеств 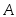 и и 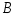 и обозначается и обозначается  . Например, . Например, 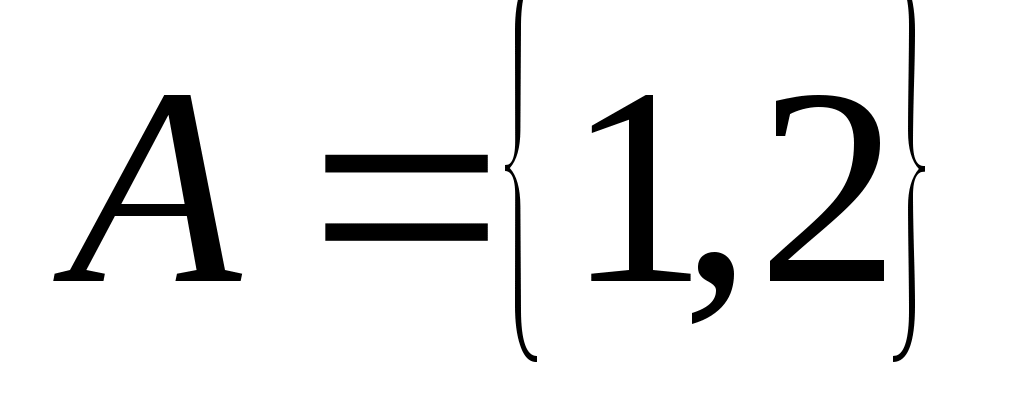 , , 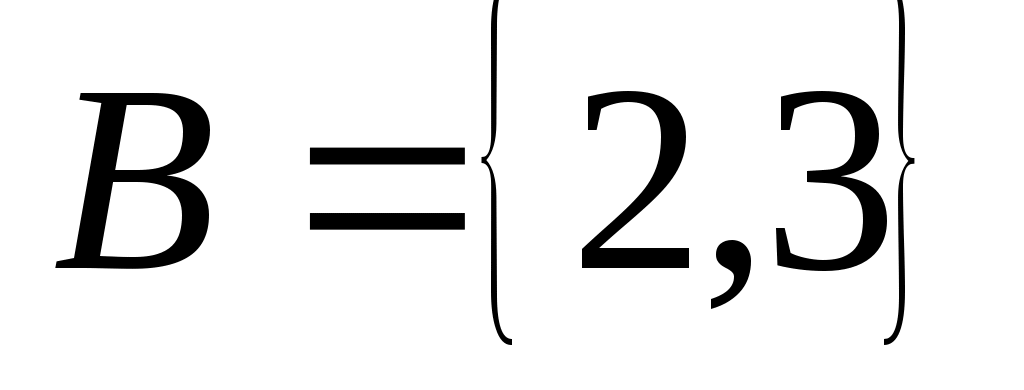  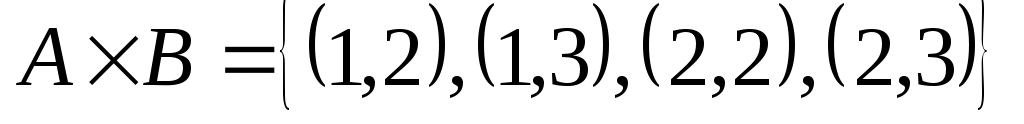 , а , а 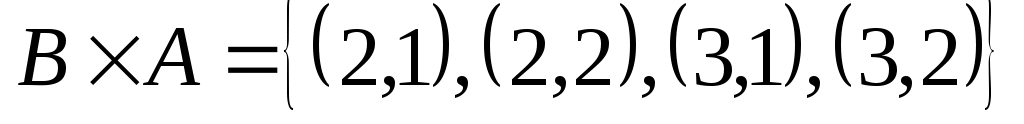 . Таким образом, декартово произведение не подчиняется коммутативному закону, и . Таким образом, декартово произведение не подчиняется коммутативному закону, и 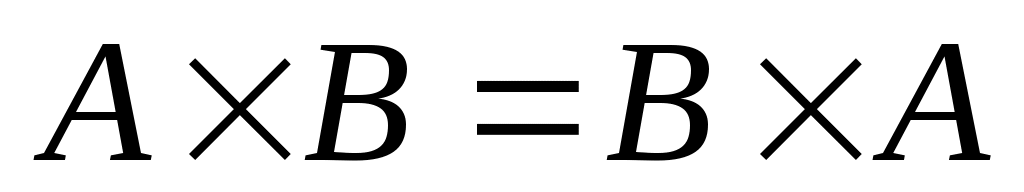 справедливо, если справедливо, если 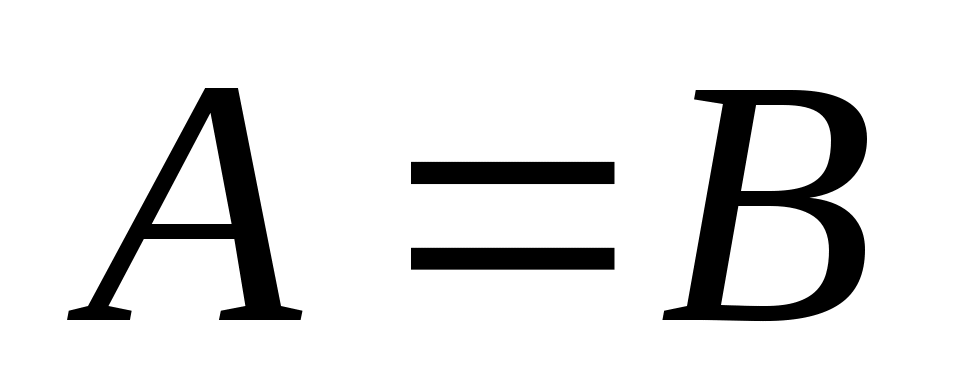 . Произведение . Произведение 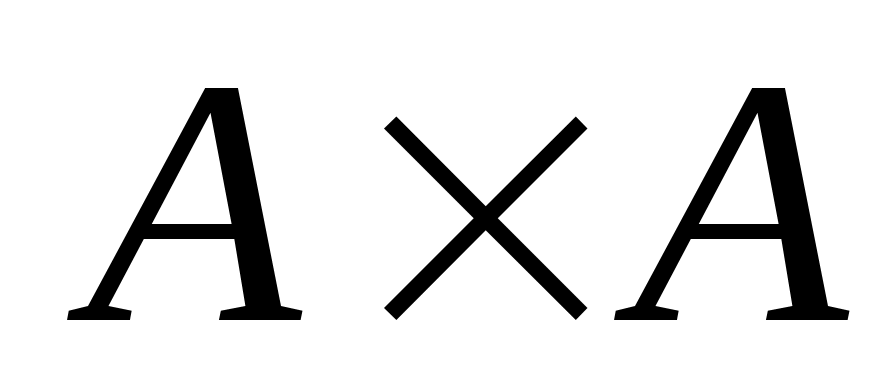 называется декартовым квадратом. называется декартовым квадратом.
Свойства операций объединения, пересечения и дополнения иногда называются законами алгебры множеств. Эти законы аналогичны правилам для равносильностей в булевой алгебре (1.13.1)—(1.13.3).
Часто элементы разных множеств связаны различными соотношениями, например, соотношениями порядка. 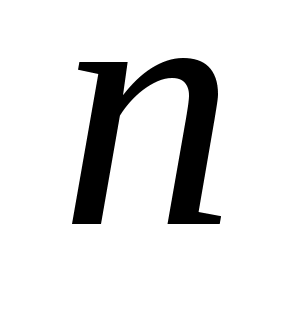 -местным отношением или -местным отношением или 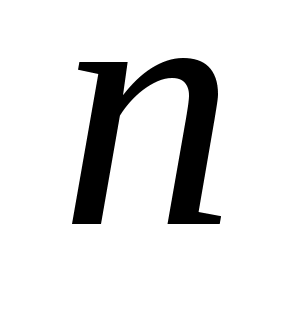 -местным предикатом -местным предикатом 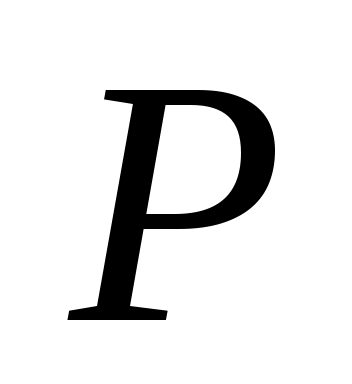 на множествах на множествах  называется любое подмножество декартова произведения называется любое подмножество декартова произведения 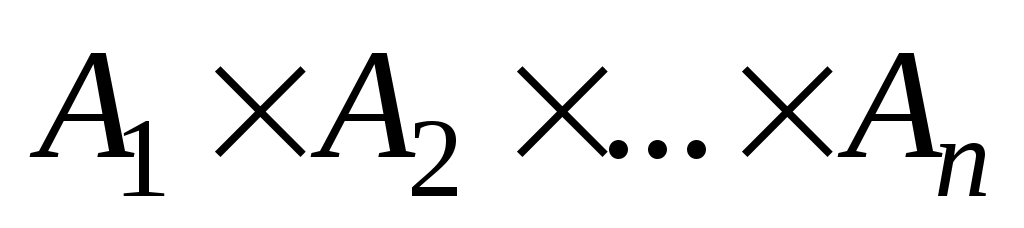 . Обозначение . Обозначение 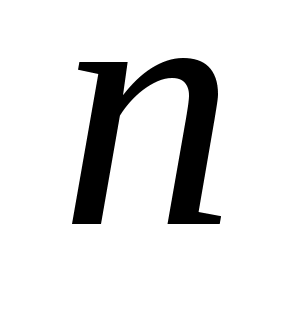 -местного отношения -местного отношения 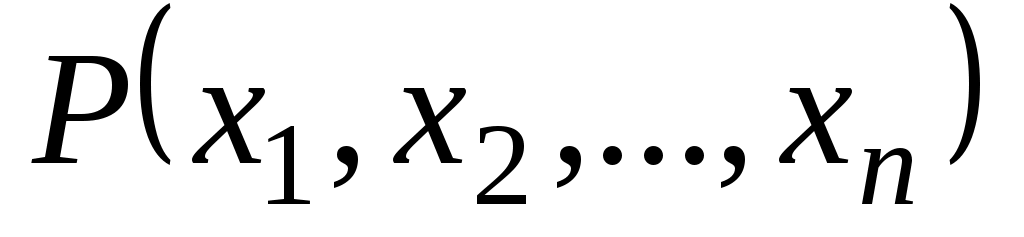 . При . При 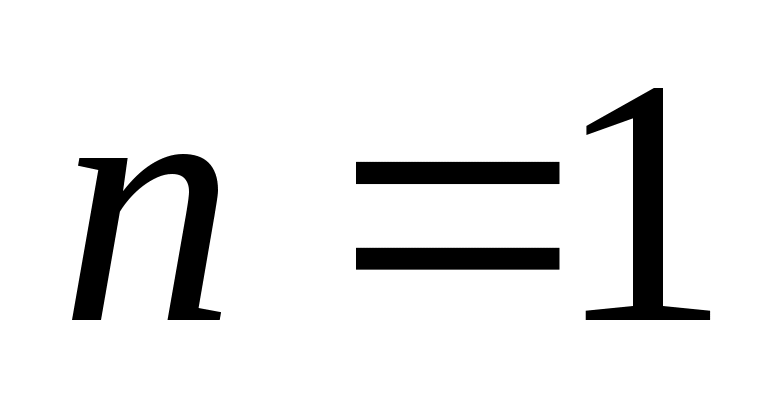 отношение отношение 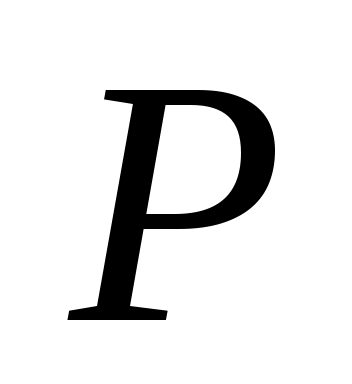 называется унарным и является подмножеством множества называется унарным и является подмножеством множества  . Бинарным (или двуместным при . Бинарным (или двуместным при 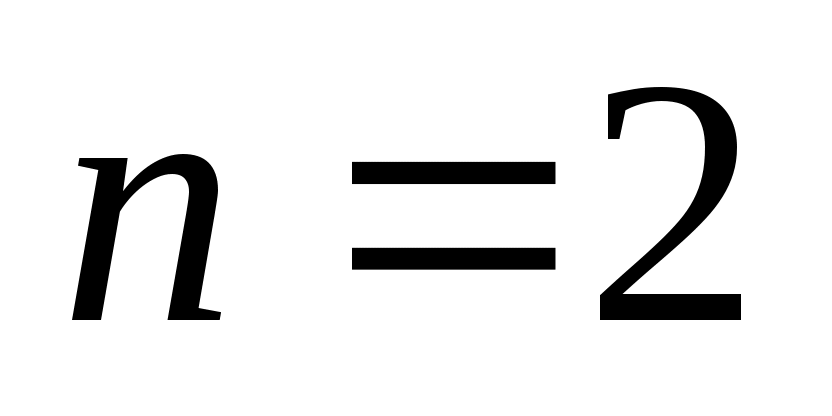 ) отношением называется множество упорядоченных пар. Элементы ) отношением называется множество упорядоченных пар. Элементы 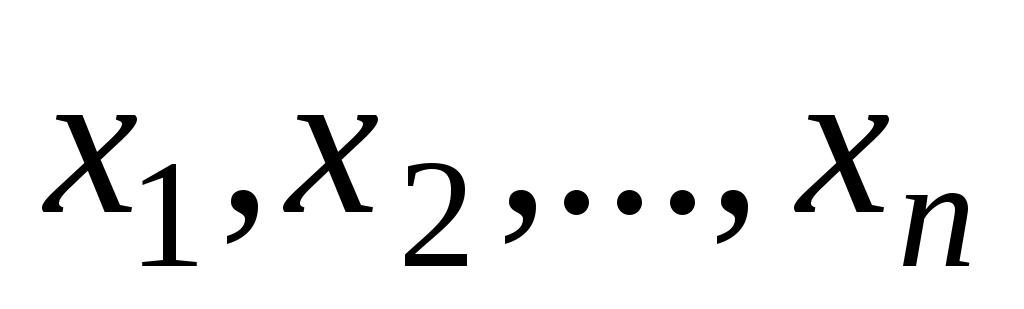 называются координатами или компонентами отношения называются координатами или компонентами отношения 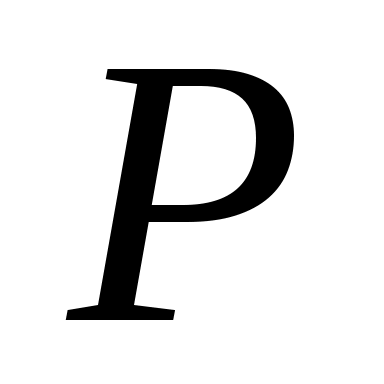 . .
В теории множеств важную роль играют два вида специальных бинарных отношений: отношения эквивалентности и отношения порядка. Прообразами этих отношений служат интуитивные понятия равенства, предшествования и предпочтения.
Рассмотрим два конечных множества 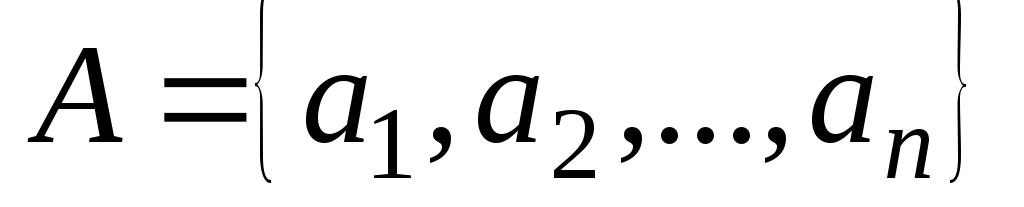 , , 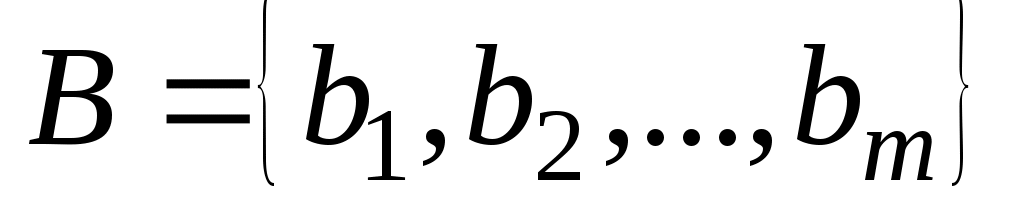 и бинарное отношение и бинарное отношение 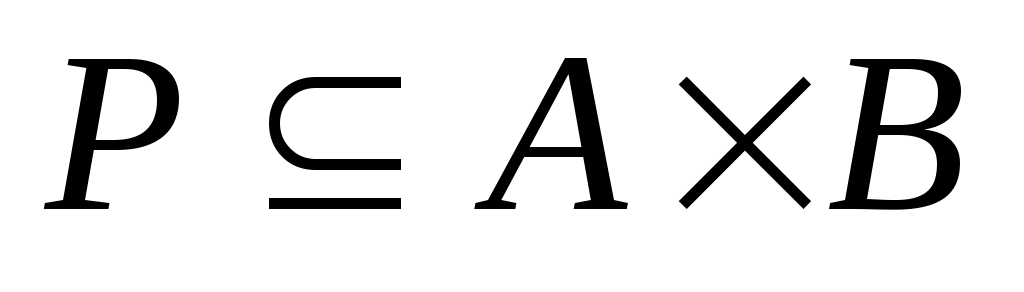 . Введем матрицу . Введем матрицу 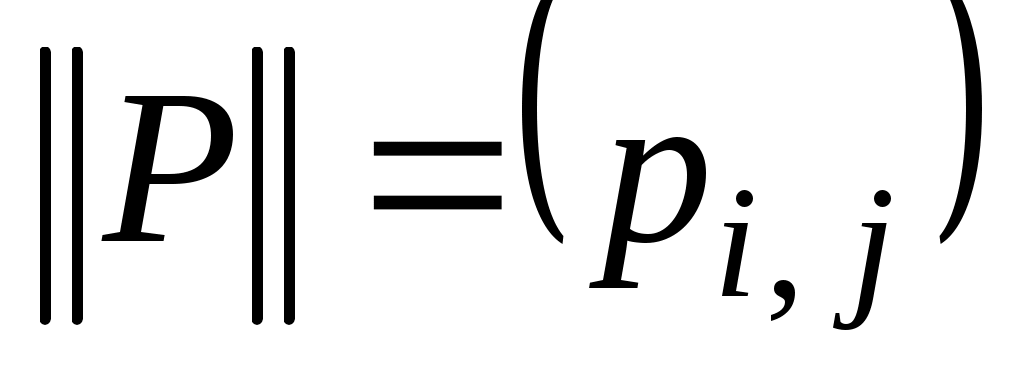 бинарного отношения бинарного отношения 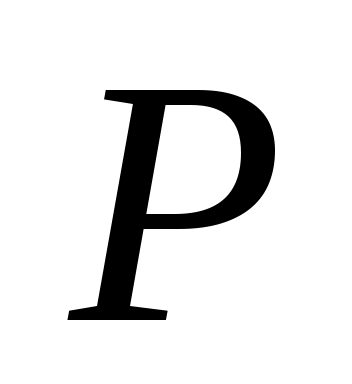 следующим образом: следующим образом:
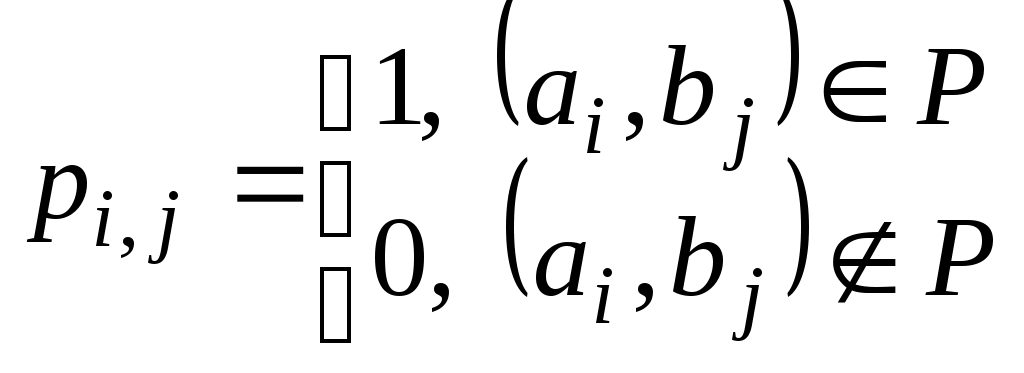 . .
Эта матрица содержит полную информацию о связях между элементами множеств  и и 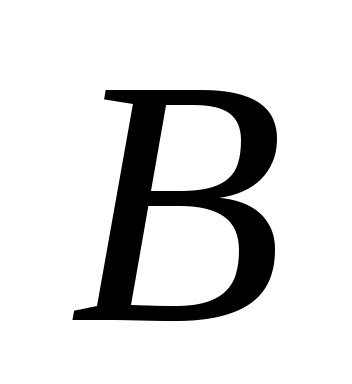 и позволяет представить эту информацию в графическом виде. и позволяет представить эту информацию в графическом виде.
Матрица любого бинарного отношения обладает следующими свойствами:
если  и и 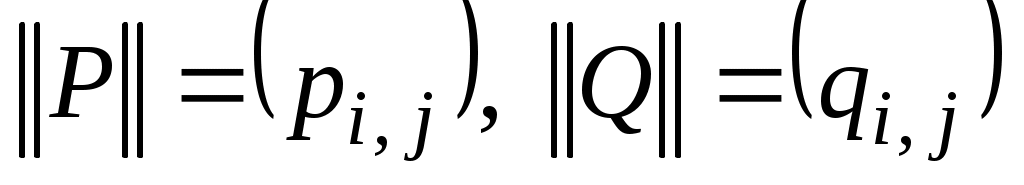 , то , то 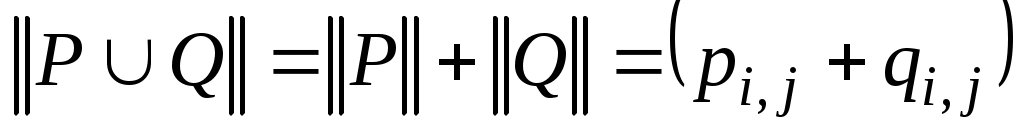 ; ; 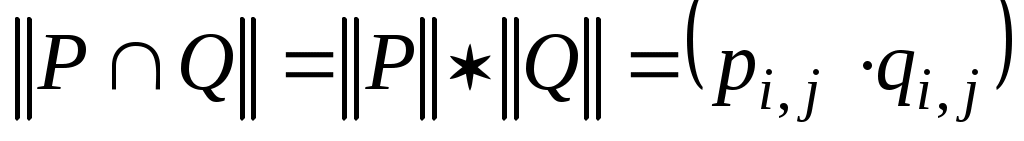 , причем сложение элементов матрицы осуществляется по правилам 0 + 0 = 0, 1 + 1 = 1, 1 + 0 = 0 + 1 = 1, а умножение осуществляется почленно обычным образом, т. е. по правилам , причем сложение элементов матрицы осуществляется по правилам 0 + 0 = 0, 1 + 1 = 1, 1 + 0 = 0 + 1 = 1, а умножение осуществляется почленно обычным образом, т. е. по правилам 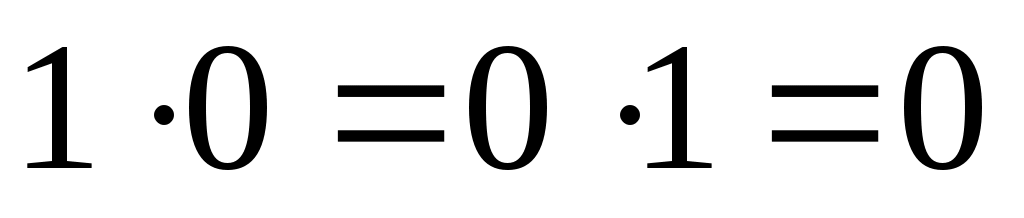 , , 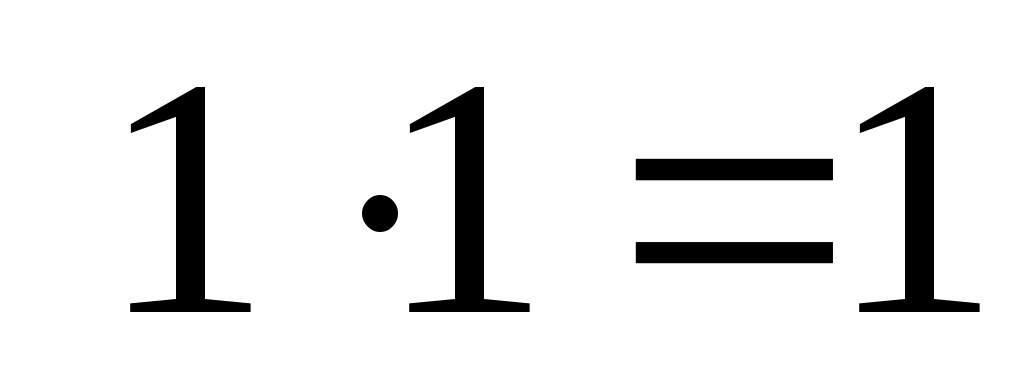 ; ;
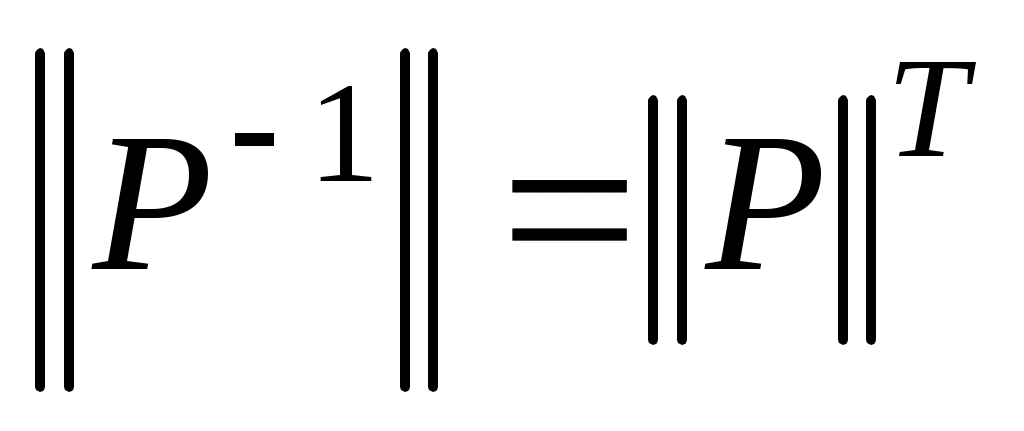 , где , где 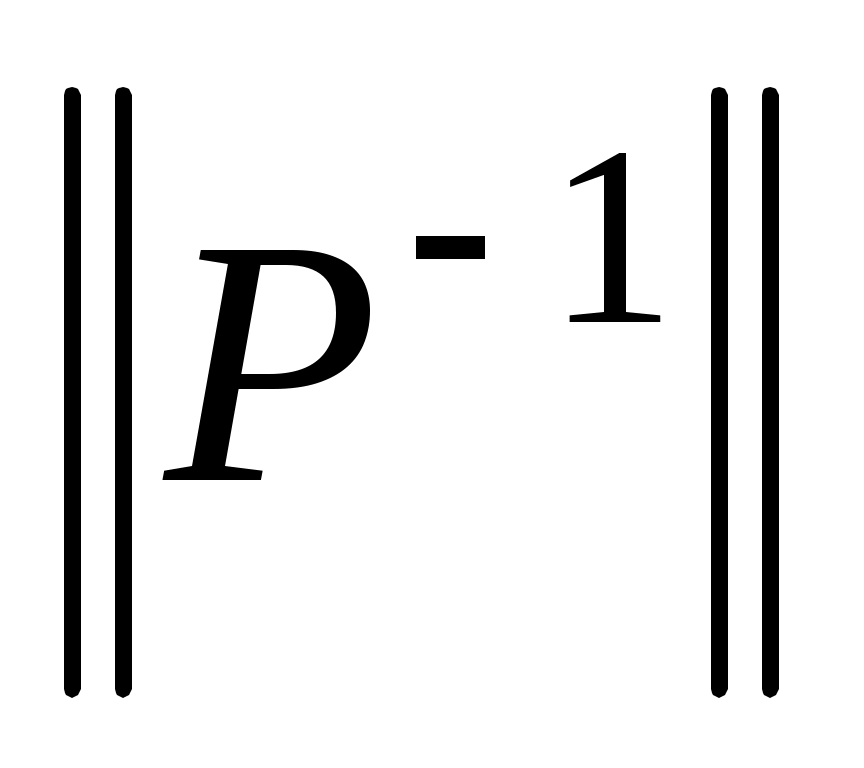 — матрица обратного отношения — матрица обратного отношения 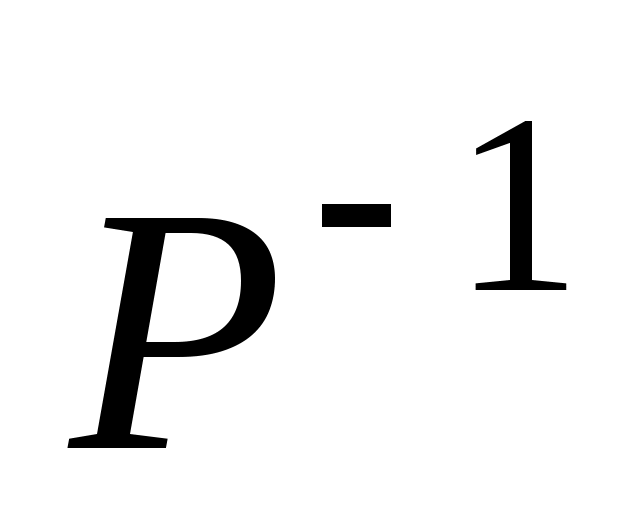 ; ;
если 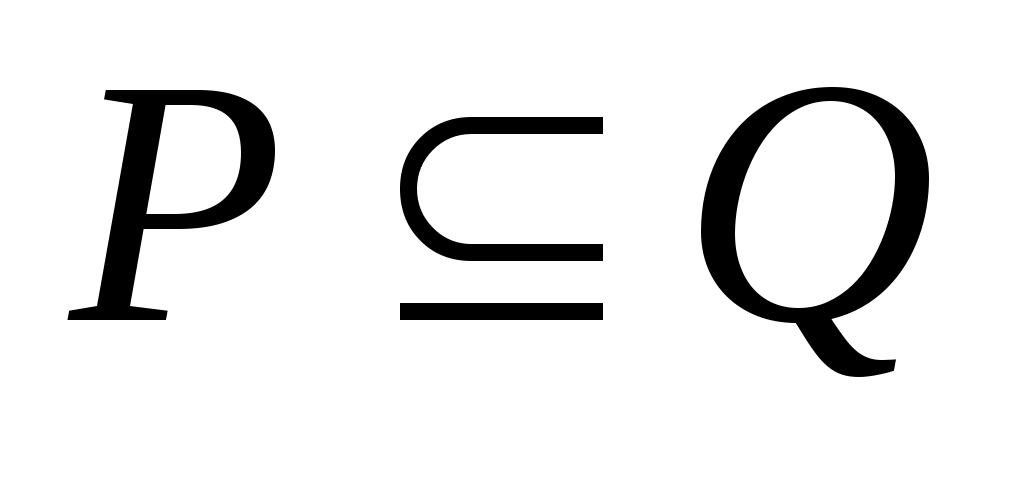 , то , то 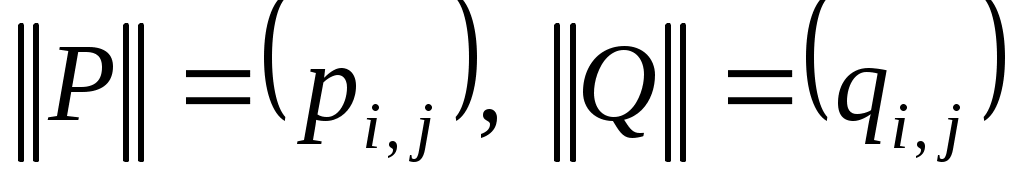 и и 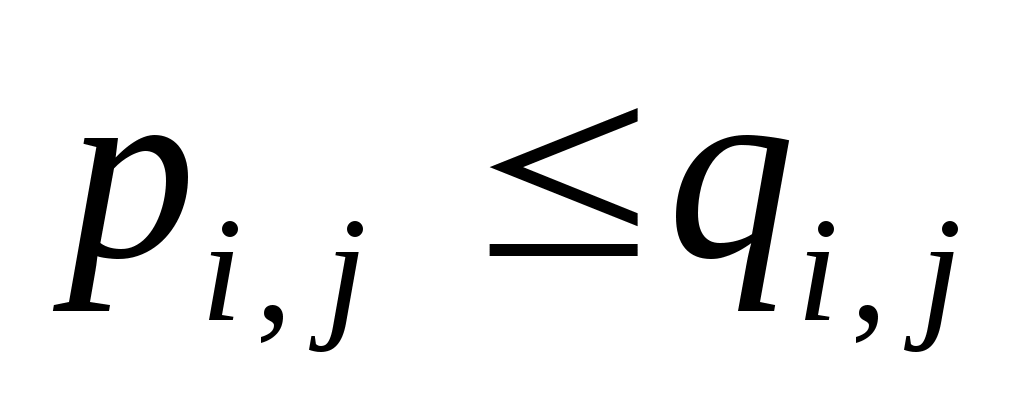 . .
Пример 1. Бинарное отношение 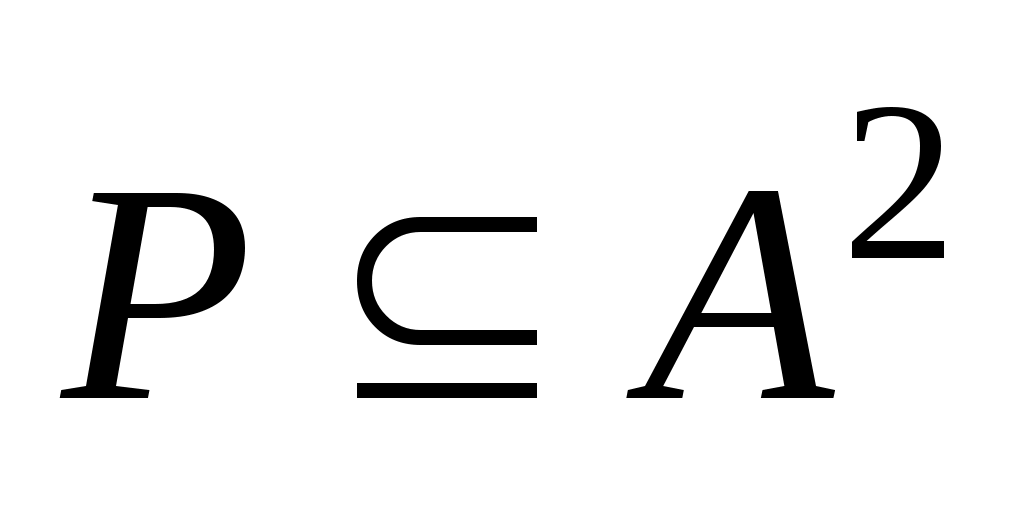 , , 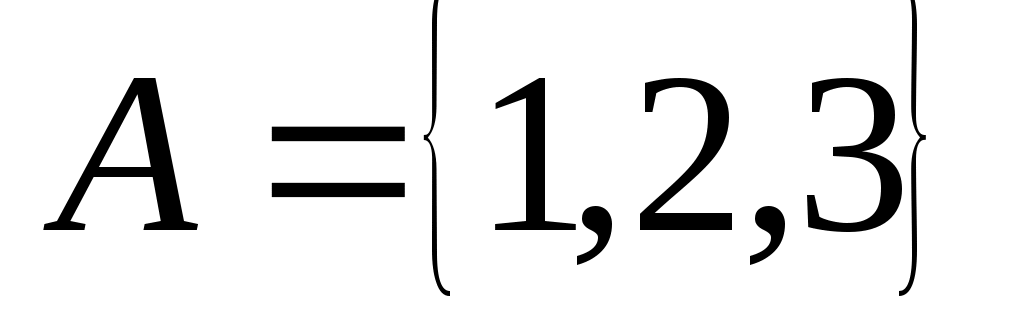 изображено на рис. 1.12. Его матрица имеет вид: изображено на рис. 1.12. Его матрица имеет вид:
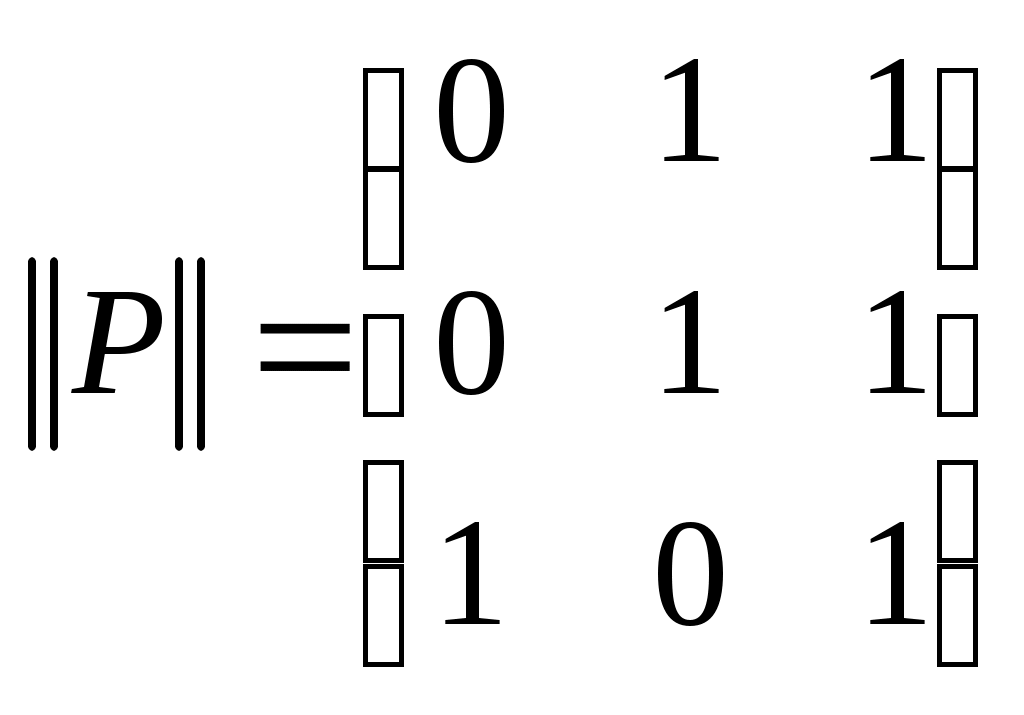 . .
Пусть
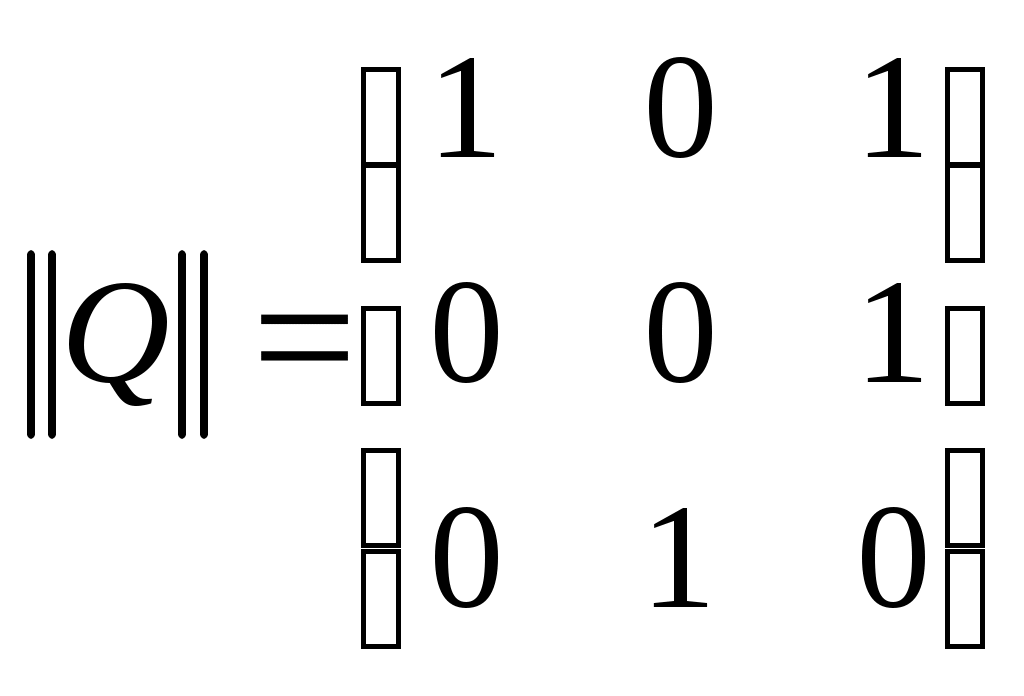 , ,
тогда
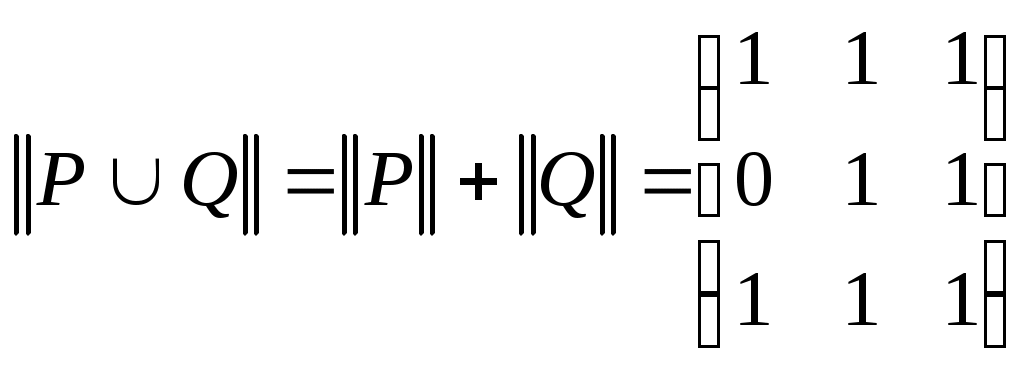 , , 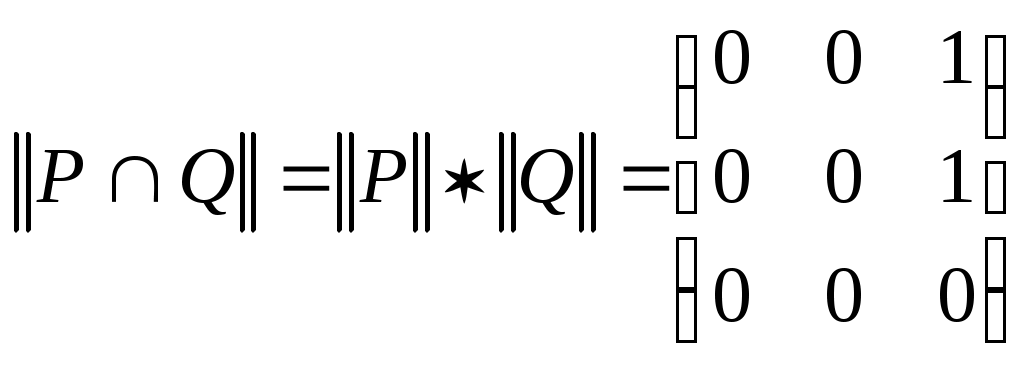 . .
Р
ис. 1.12. Бинарное отношение 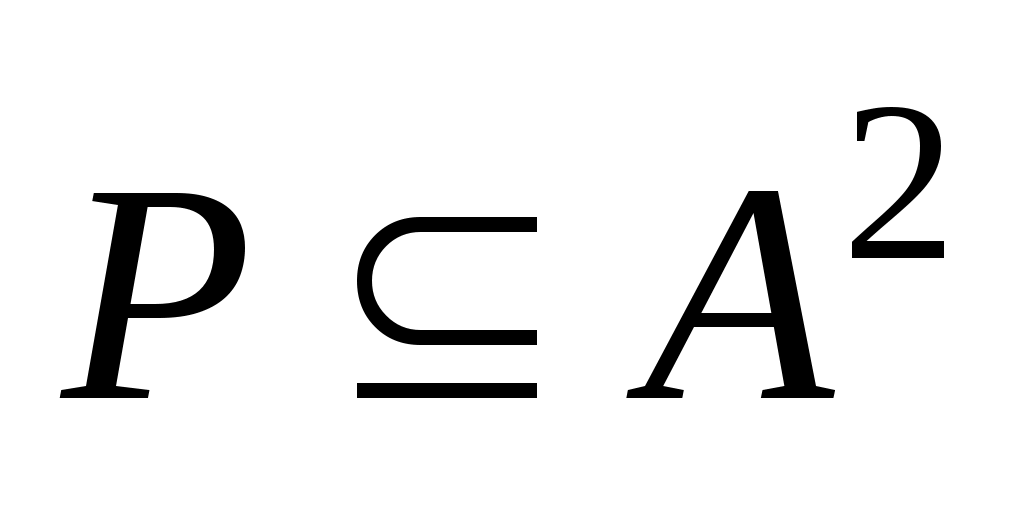 , , 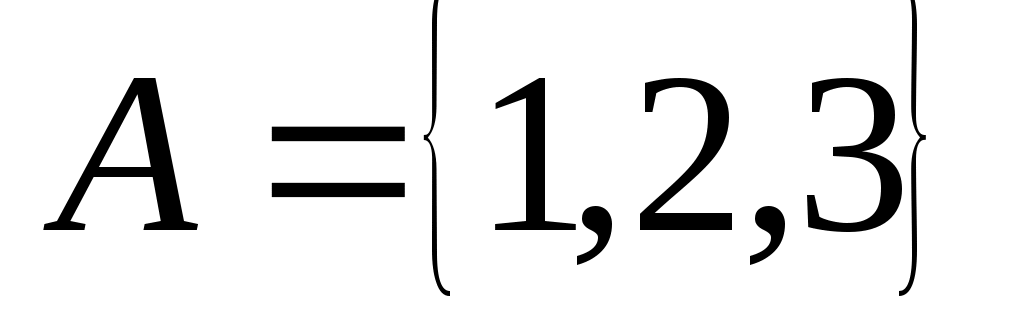
Пусть  — бинарное отношение на множестве — бинарное отношение на множестве  , , 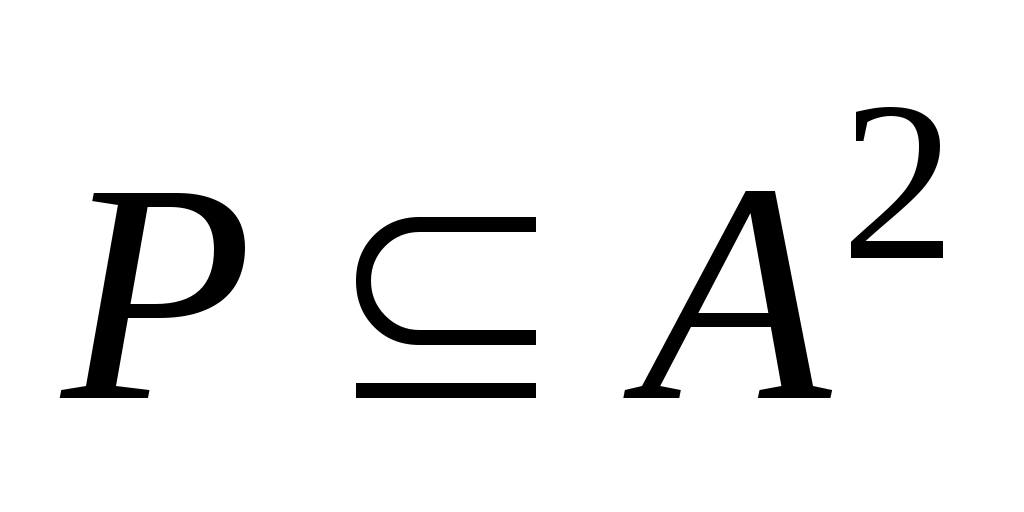 . Отношение . Отношение 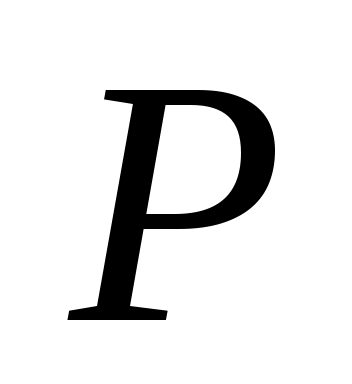 на множестве на множестве  называется рефлексивным, если называется рефлексивным, если 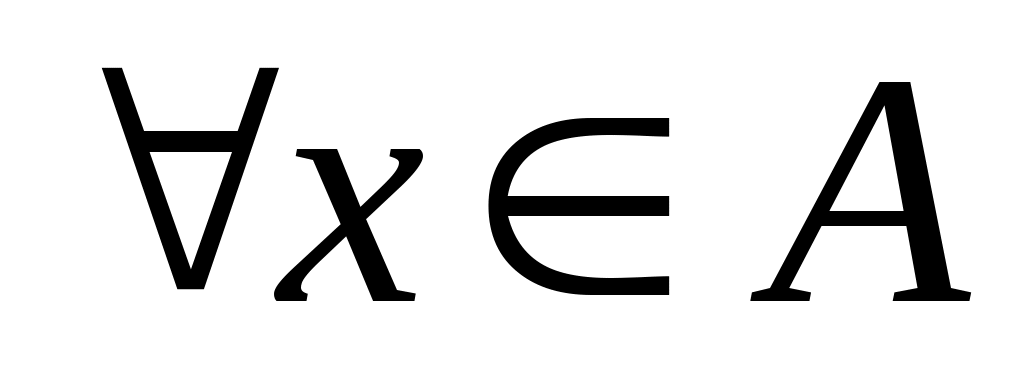 , , 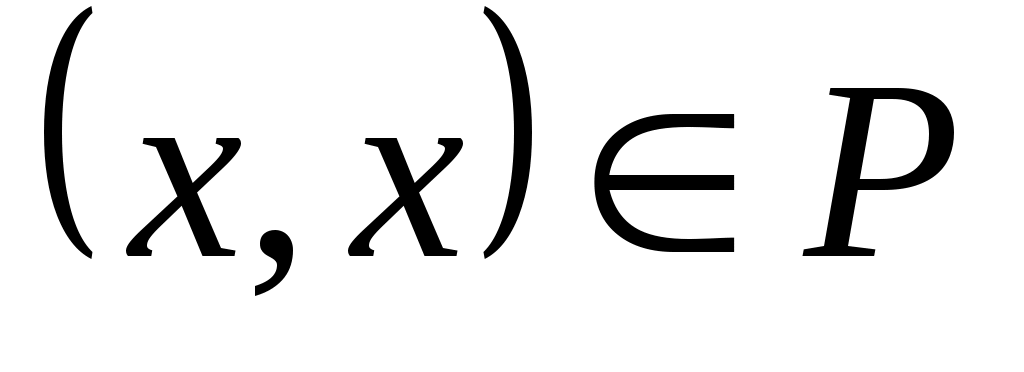 , т. е. , т. е.
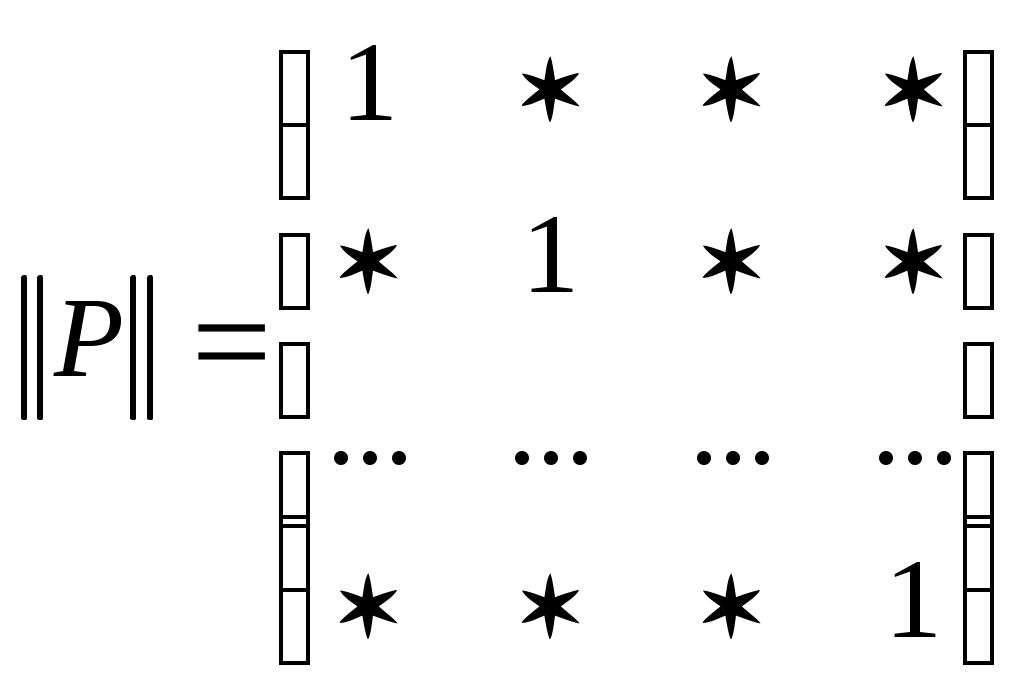 , ,
где звездочкой обозначены нули или единицы. Отношение 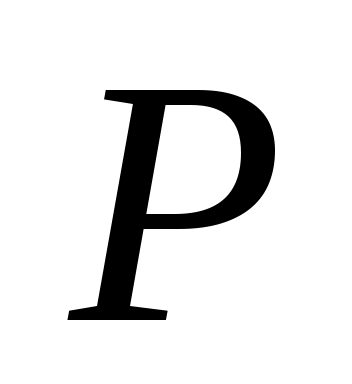 называется иррефлексивным, если называется иррефлексивным, если 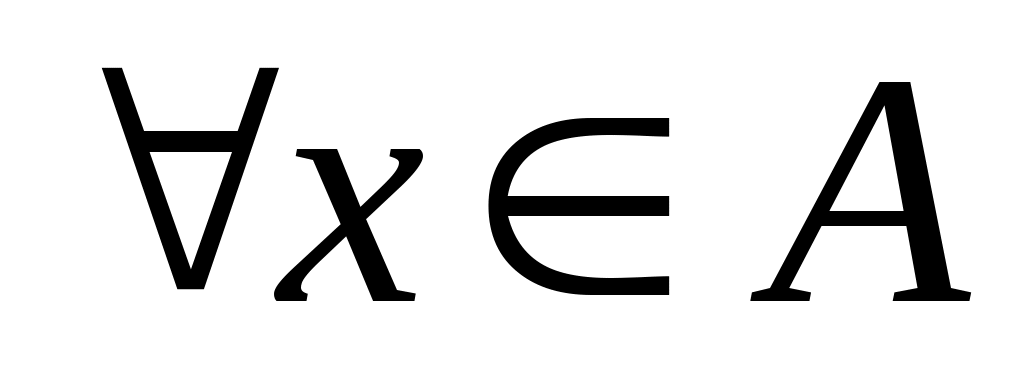 , , 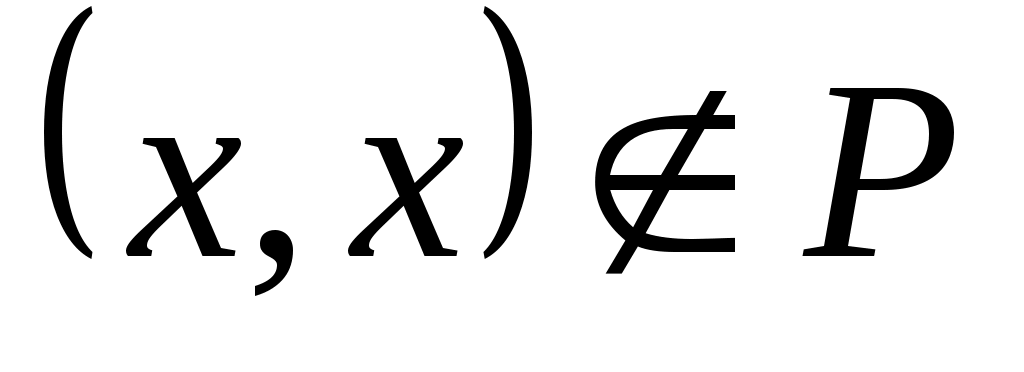 . Отношение . Отношение 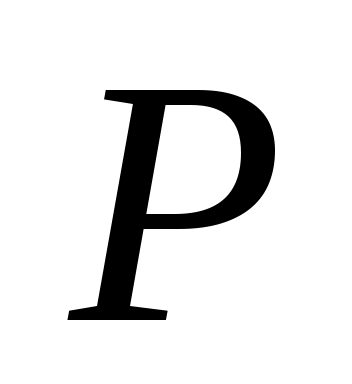 на множестве на множестве  называется симметричным, если называется симметричным, если 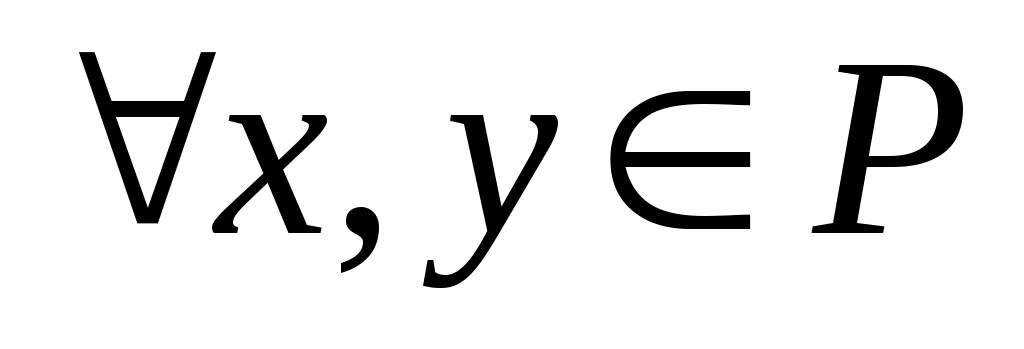 и из условия и из условия 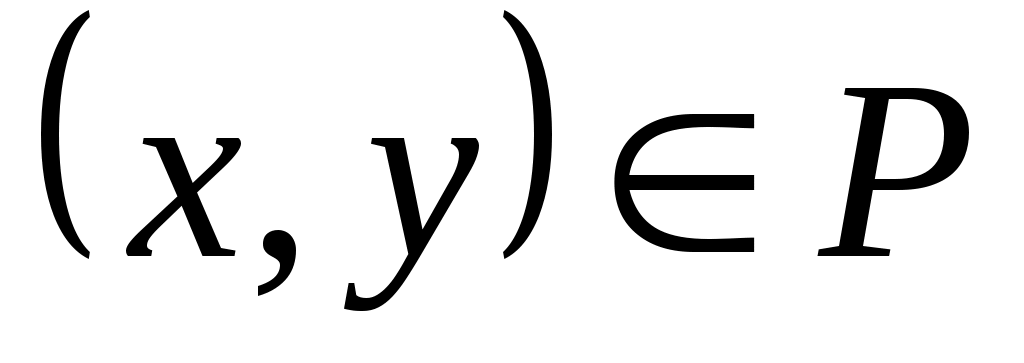 следует, что следует, что 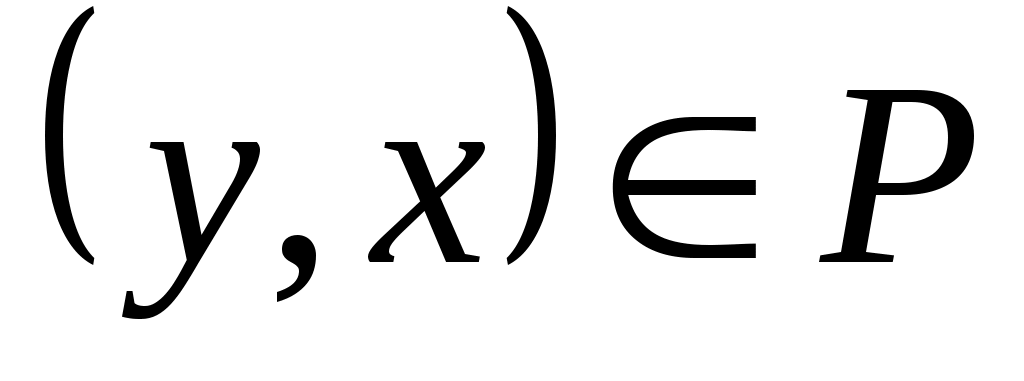 . Это значит, что . Это значит, что 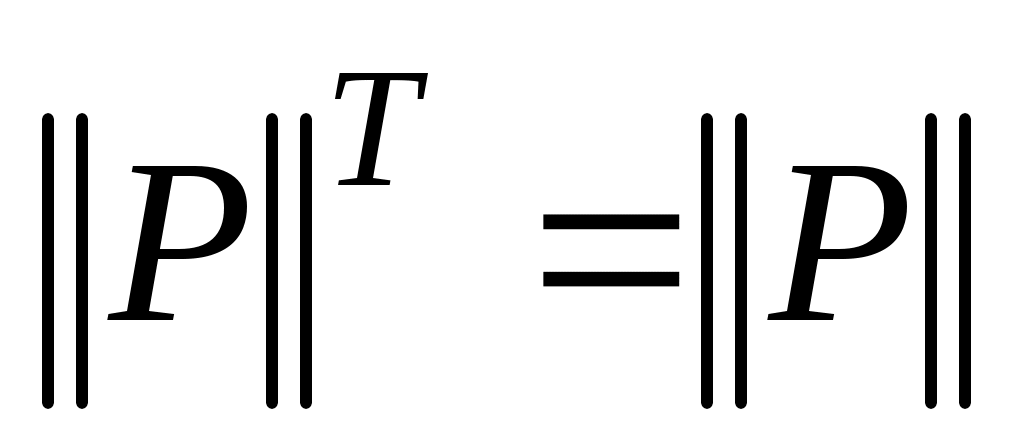 . Отношение . Отношение 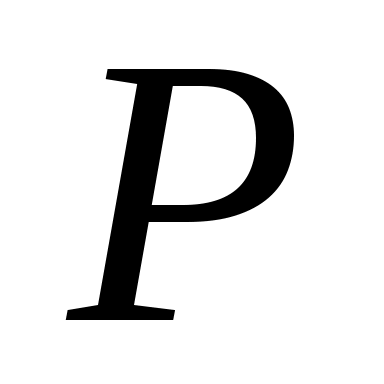 называется антисимметричным, если из условий называется антисимметричным, если из условий 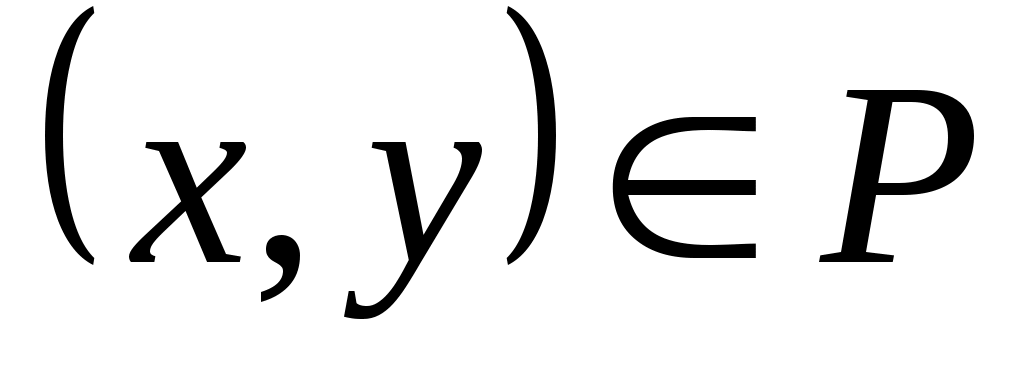 и и 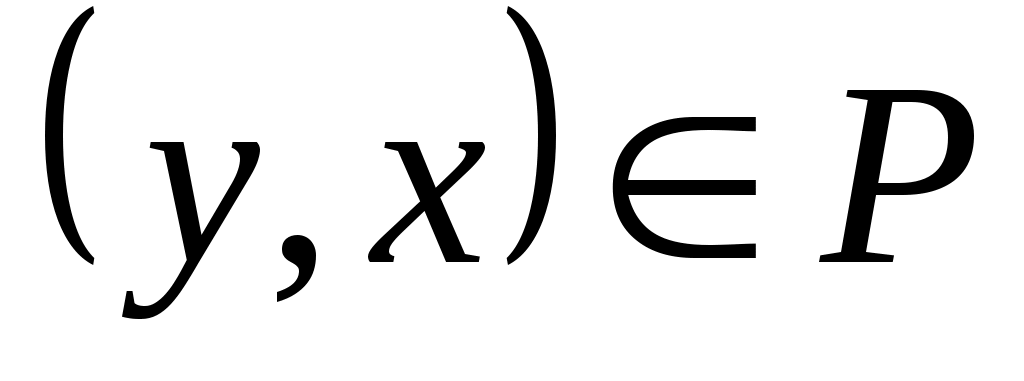 следует, что следует, что 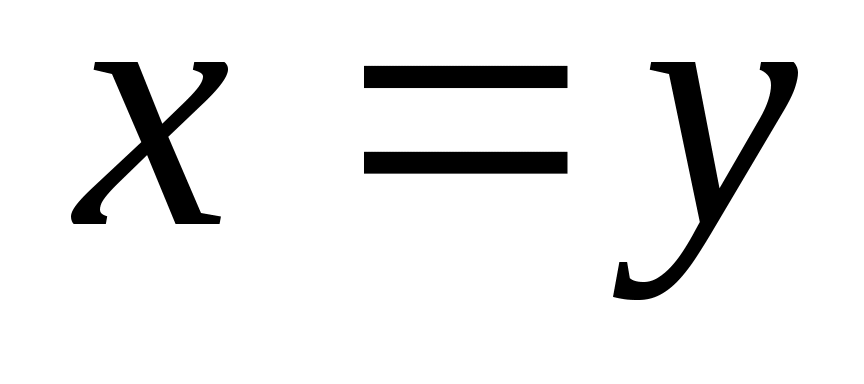 , или , или 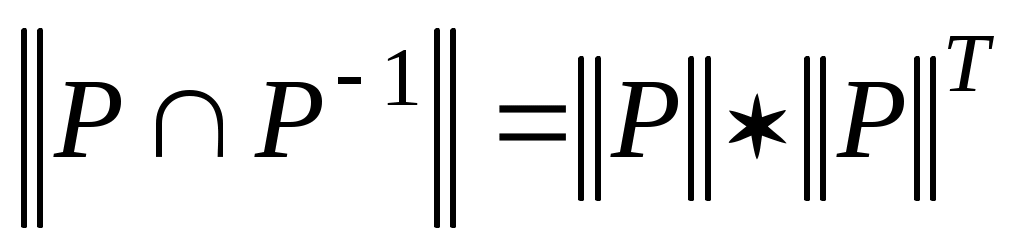 . Это свойство приводит к тому, что у матрицы . Это свойство приводит к тому, что у матрицы 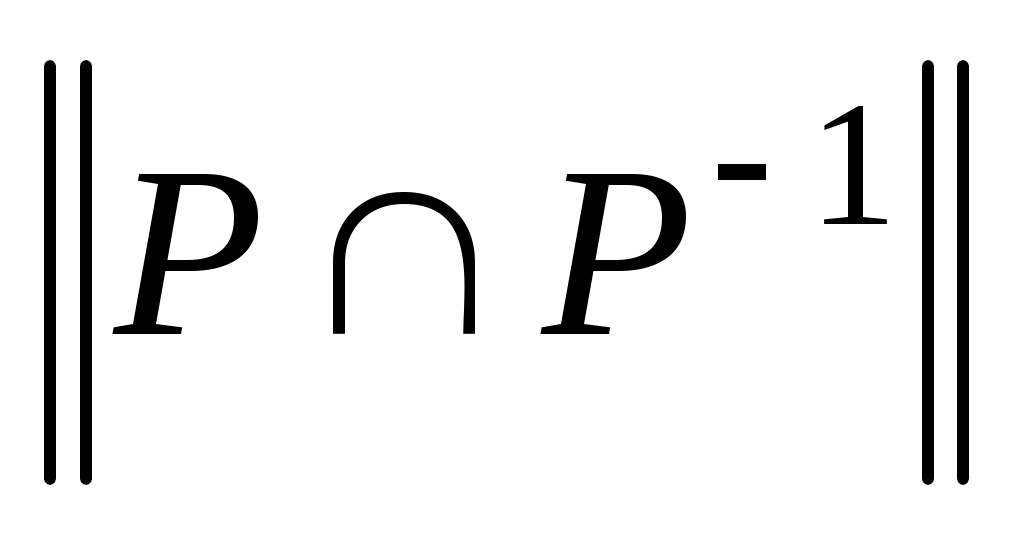 все элементы вне главной диагонали будут нулевыми (на главной диагонали тоже могут быть нули). Отношение все элементы вне главной диагонали будут нулевыми (на главной диагонали тоже могут быть нули). Отношение  называется транзитивным, если из называется транзитивным, если из 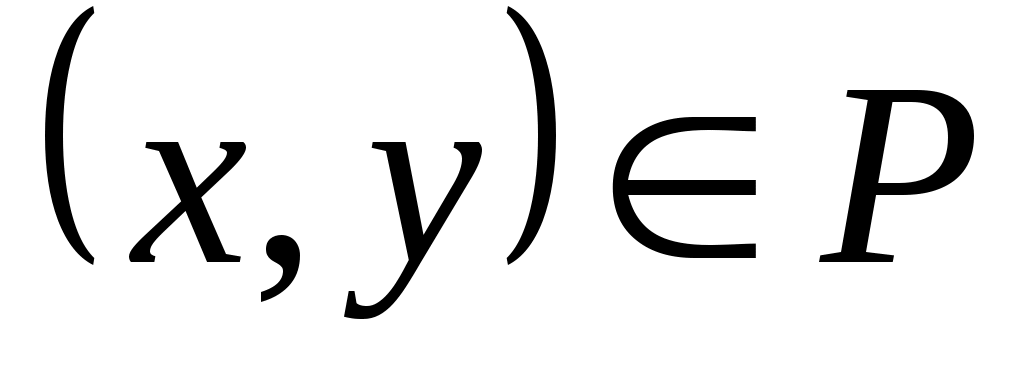 и и 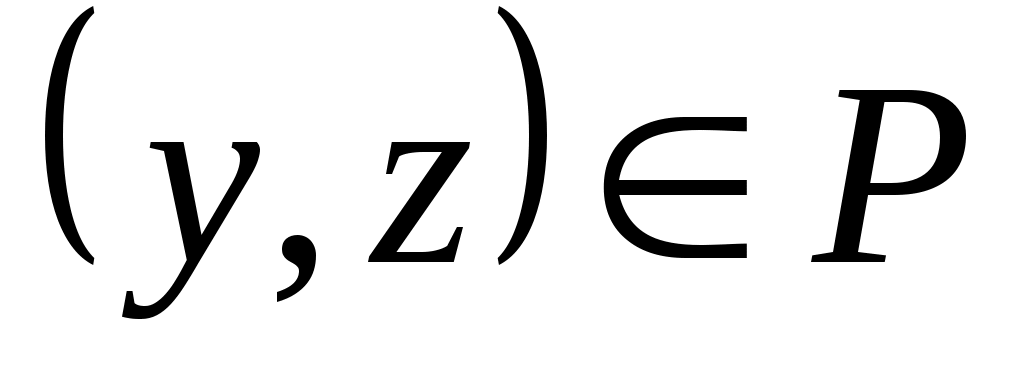 следует, что следует, что 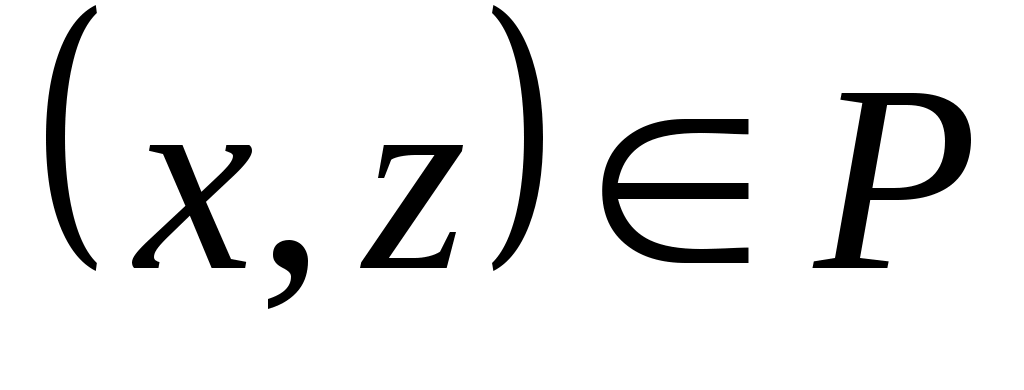 . .
Рефлексивное, транзитивное и симметричное отношение на множестве  называется эквивалентностью на называется эквивалентностью на  . Эквивалентность обозначается символами . Эквивалентность обозначается символами  или , например, или , например, 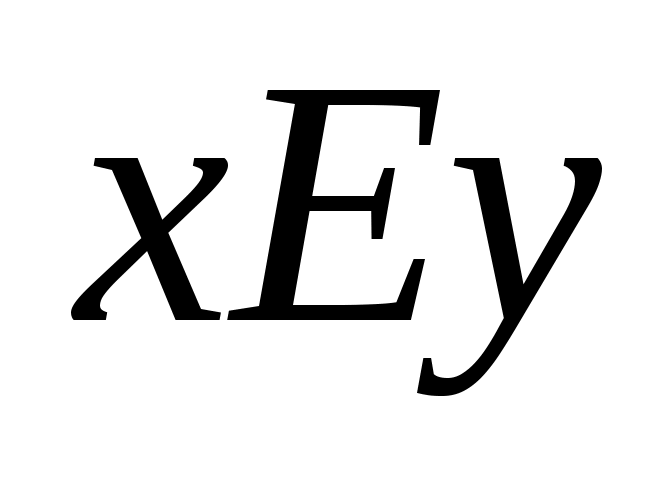 , , 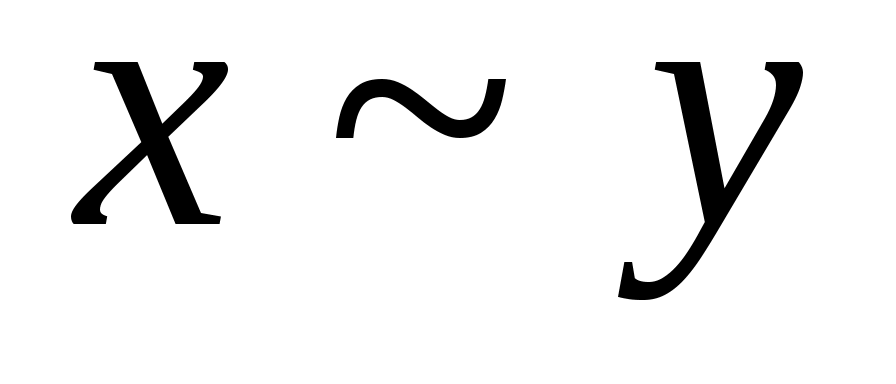 . .
Пример 2. Докажем, что на множестве 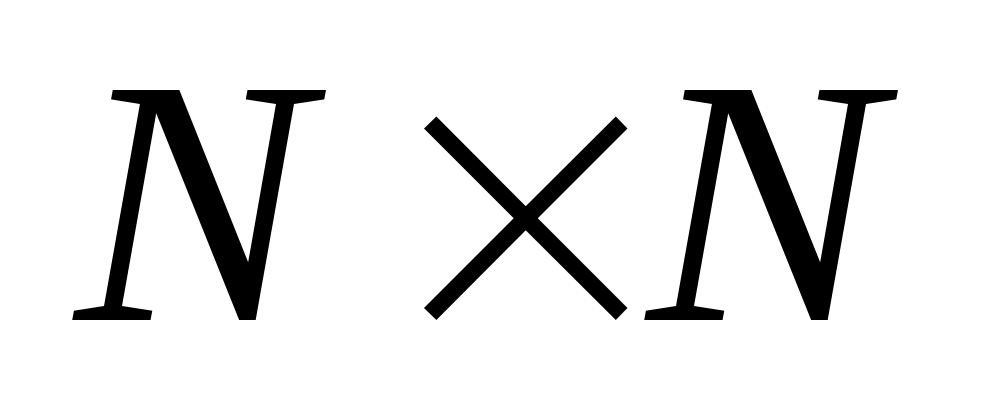 отношение отношение  является отношением эквивалентности, если является отношением эквивалентности, если 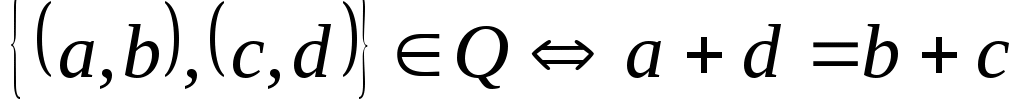 . .
Если отношение  рефлексивно на рефлексивно на  , то , то 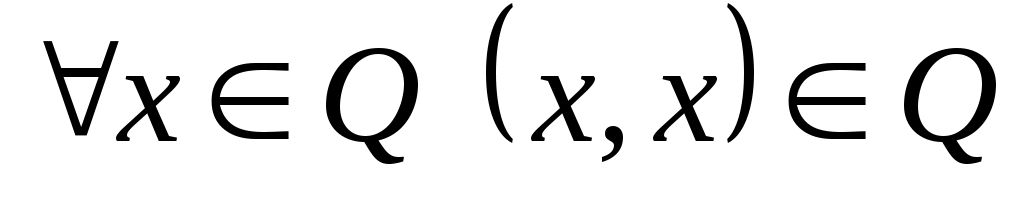 . В нашем случае роль . В нашем случае роль  играет множество играет множество 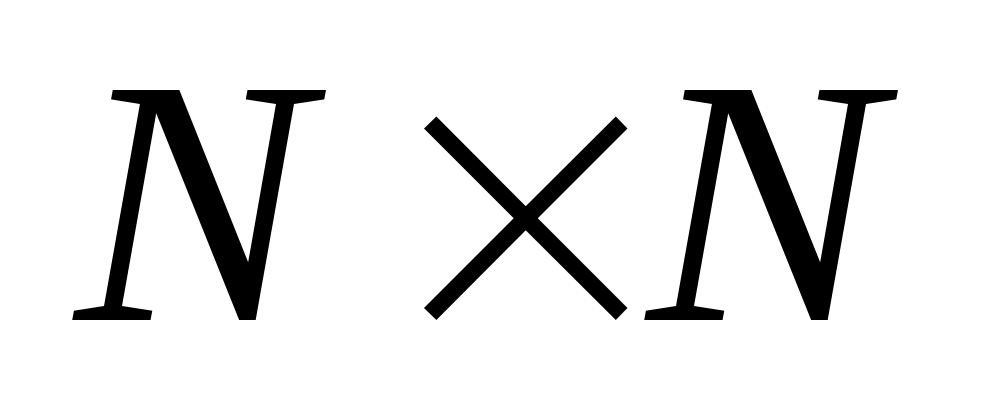 , а роль элемента , а роль элемента 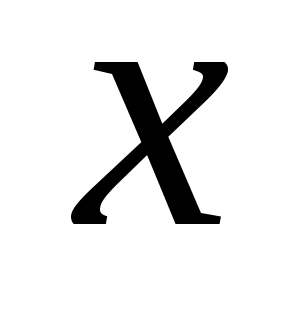 играет пара играет пара 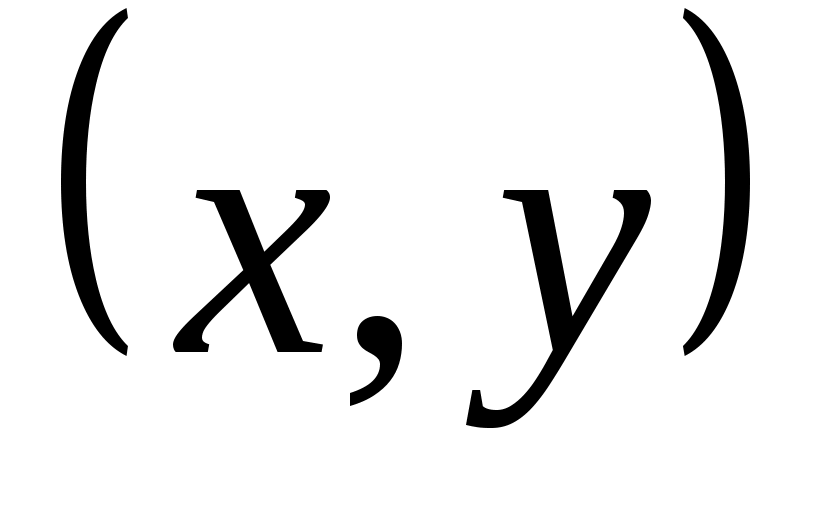 . Тогда отношение . Тогда отношение  рефлексивно на рефлексивно на  , если , если 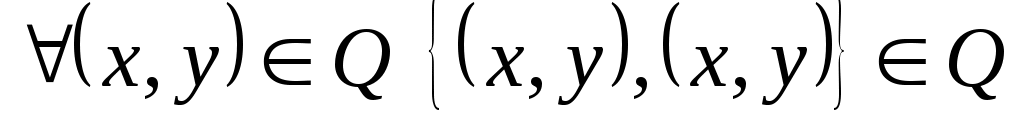 . По определению . По определению 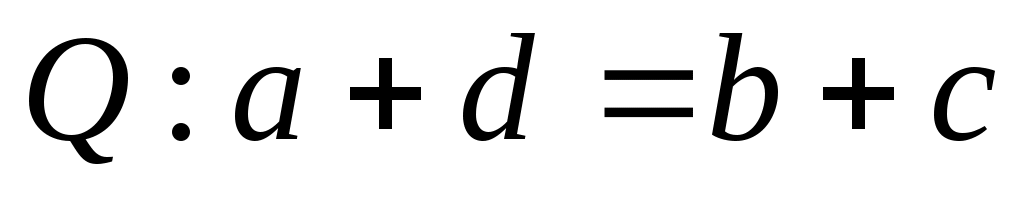 , но , но 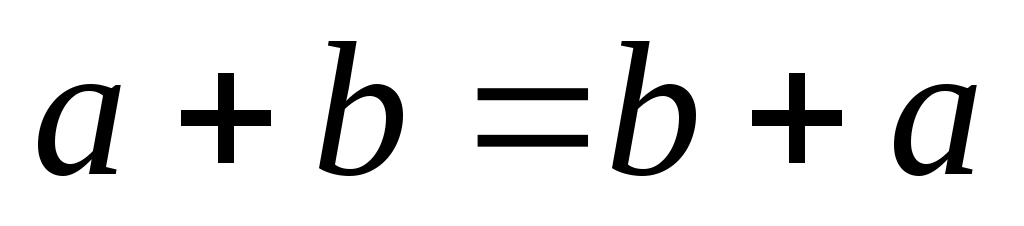 , следовательно, , следовательно,  рефлексивно. рефлексивно.
Аналогично, если 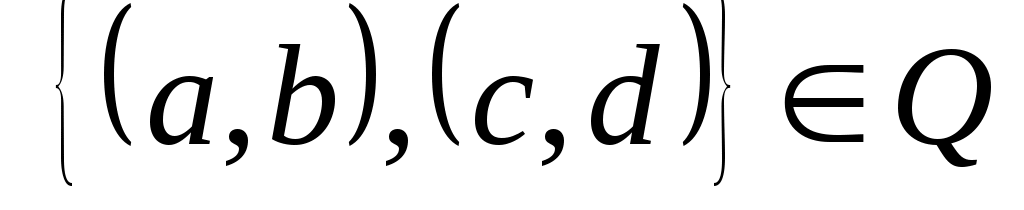 , то и , то и 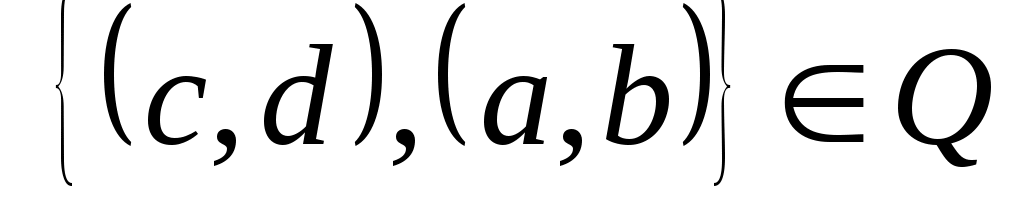 , так как из , так как из 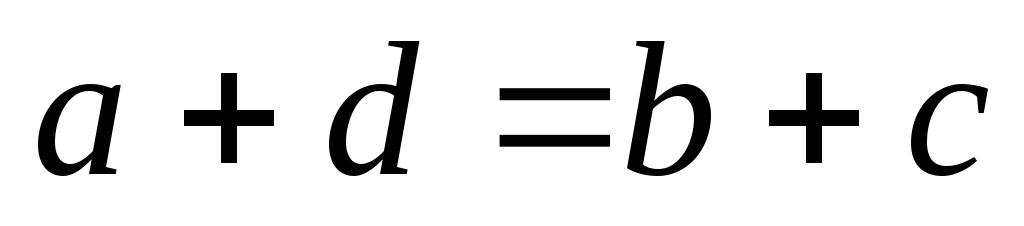 следует, что следует, что 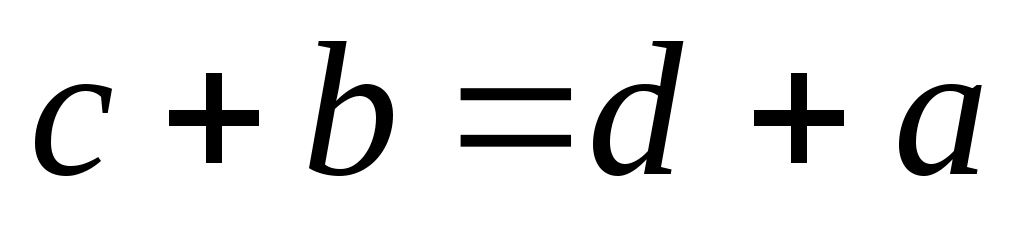 . Таким образом, . Таким образом,  симметрично. симметрично.
Наконец, если 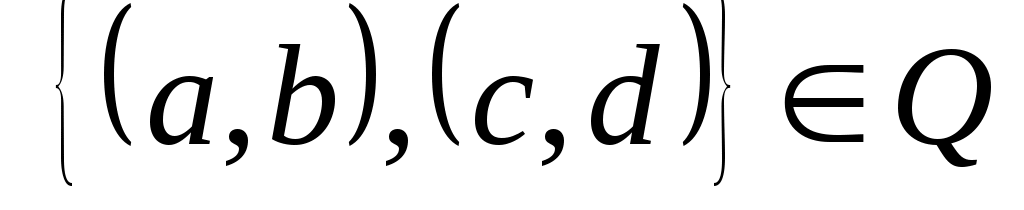 , , 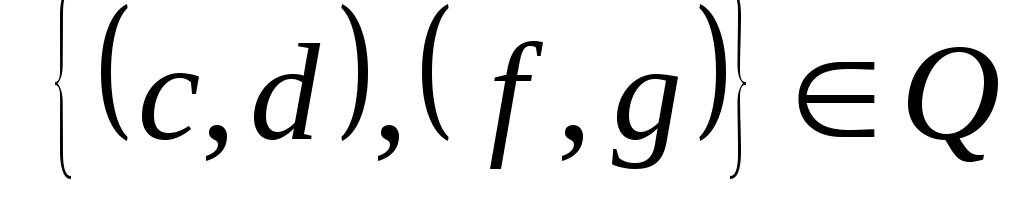 , то , то 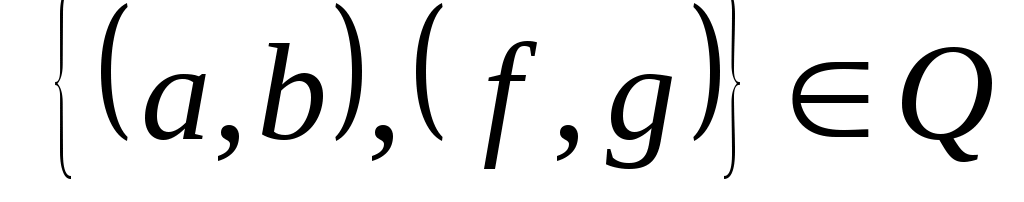 , так как , так как 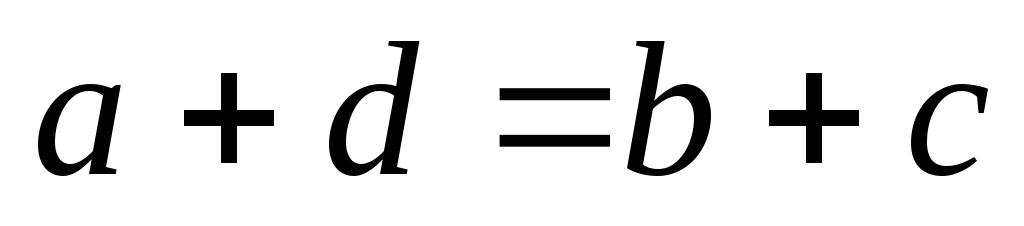 и и 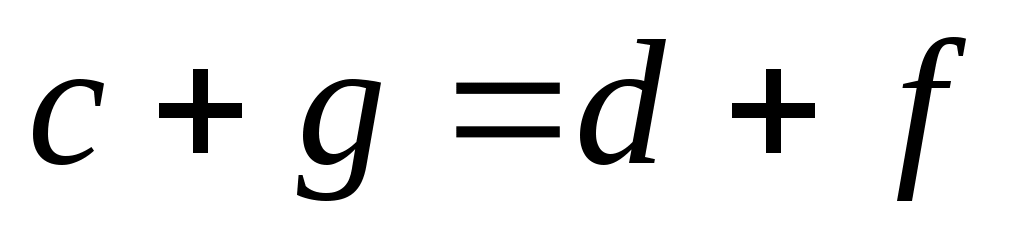 . Тогда . Тогда 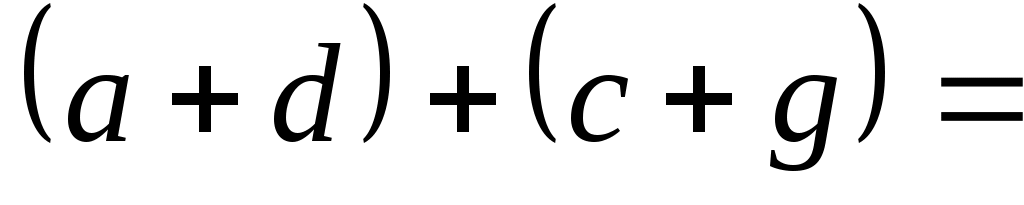 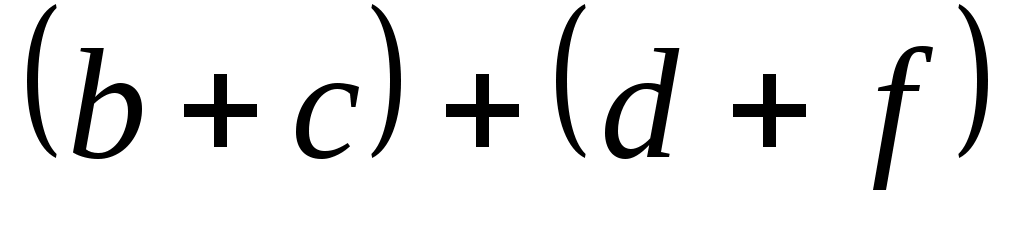 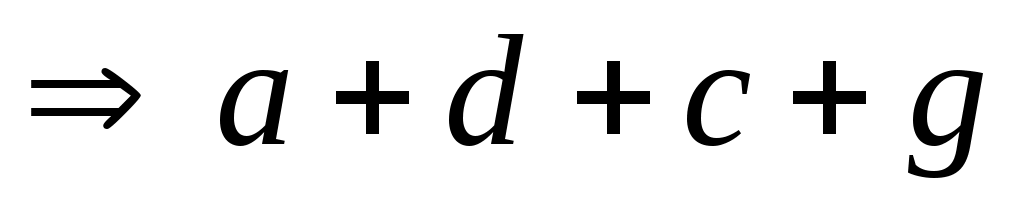 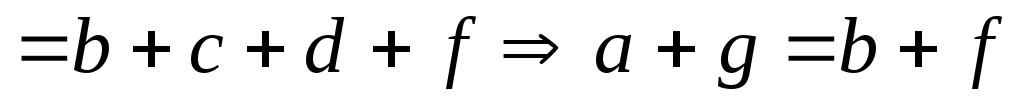 , т. е. , т. е.  транзитивно. транзитивно.
Рефлексивное, транзитивное и антисимметричное отношение на множестве  называется частичным порядком на называется частичным порядком на  . Частичный порядок обозначается символом . Частичный порядок обозначается символом 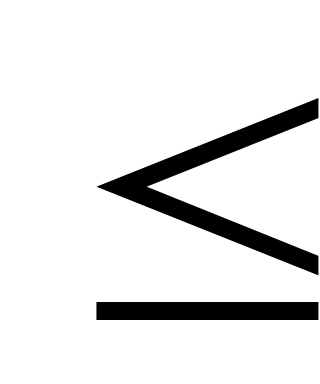 , а обратное ему отношение , а обратное ему отношение 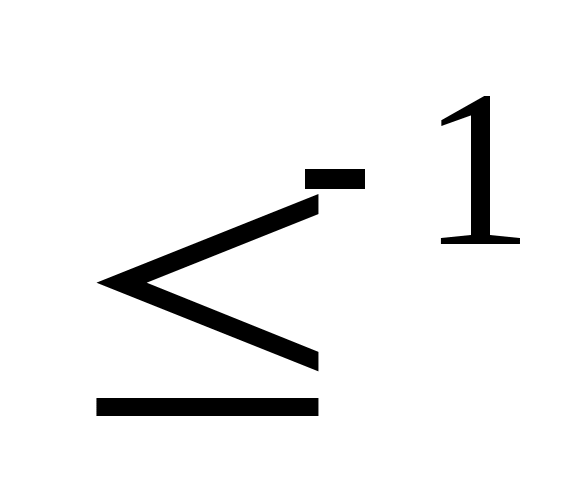 символом символом 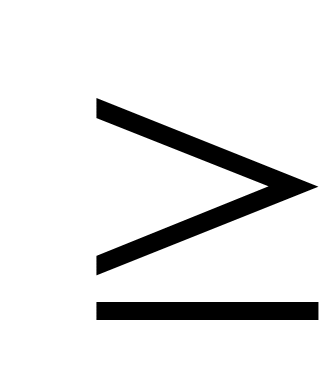 . Отношение . Отношение 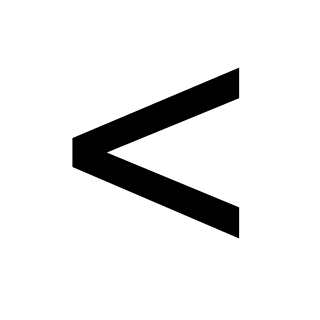 называется строгим порядком и определяется таким образом: называется строгим порядком и определяется таким образом:  и и 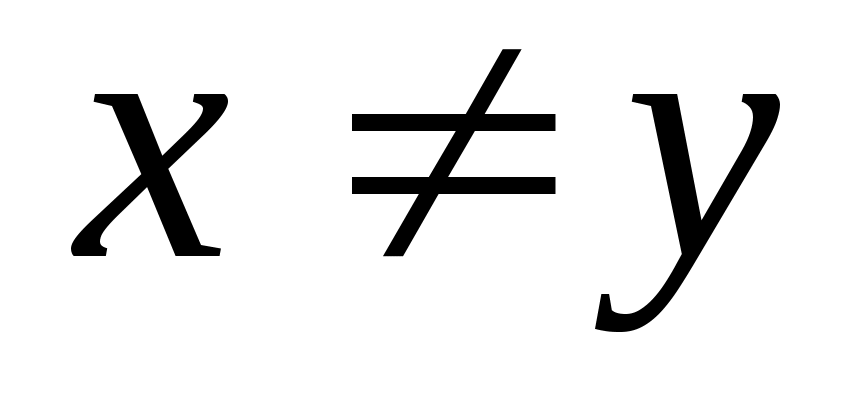 . Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности . Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности 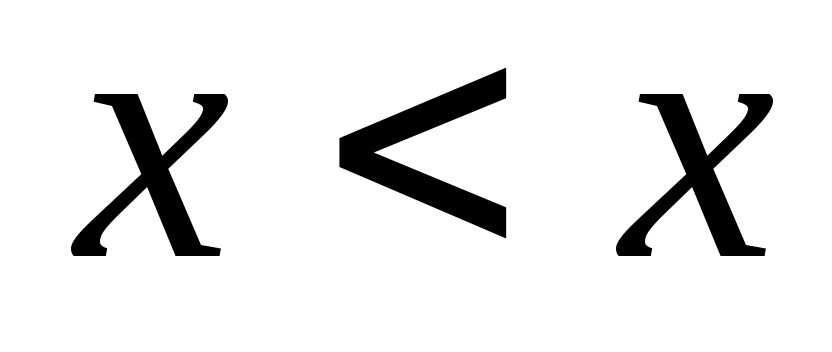 . .
Если во множестве  есть элементы есть элементы 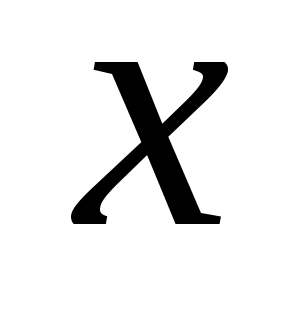 и и 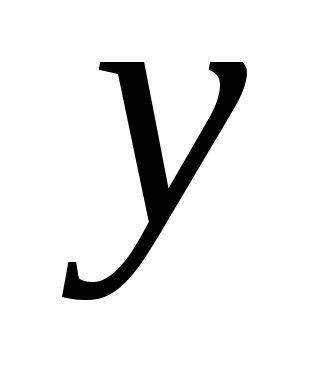 , о которых нельзя сказать, что , о которых нельзя сказать, что 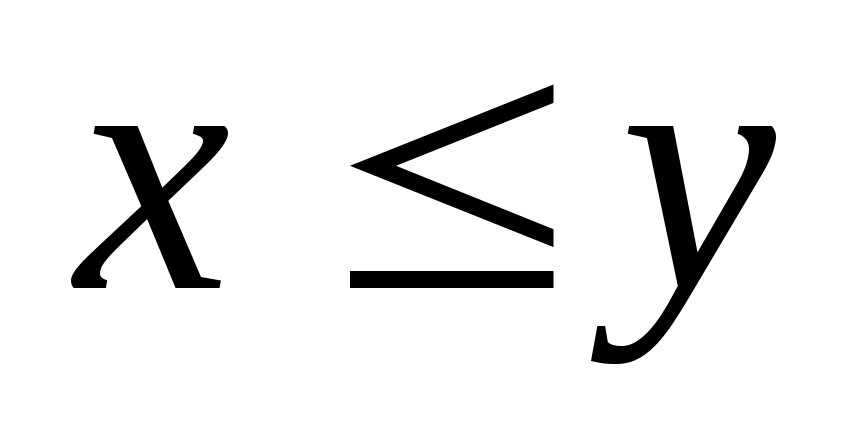 или или 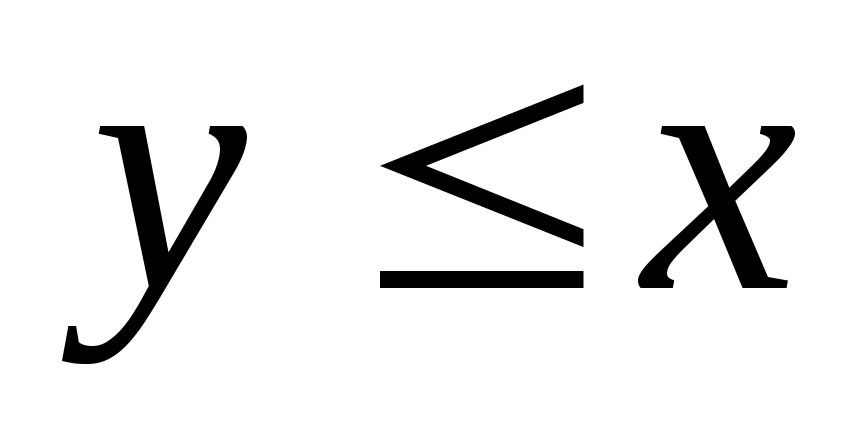 , то такие элементы называются несравнимыми. Частичный порядок называется линейным порядком, если любые два элемента , то такие элементы называются несравнимыми. Частичный порядок называется линейным порядком, если любые два элемента 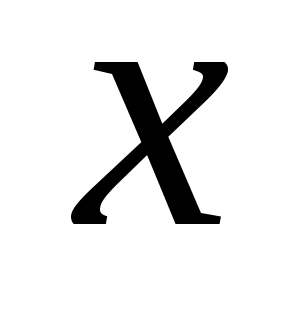 и и 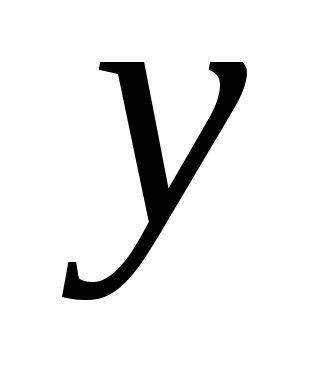 из множества из множества  сравнимы, т. е. сравнимы, т. е. 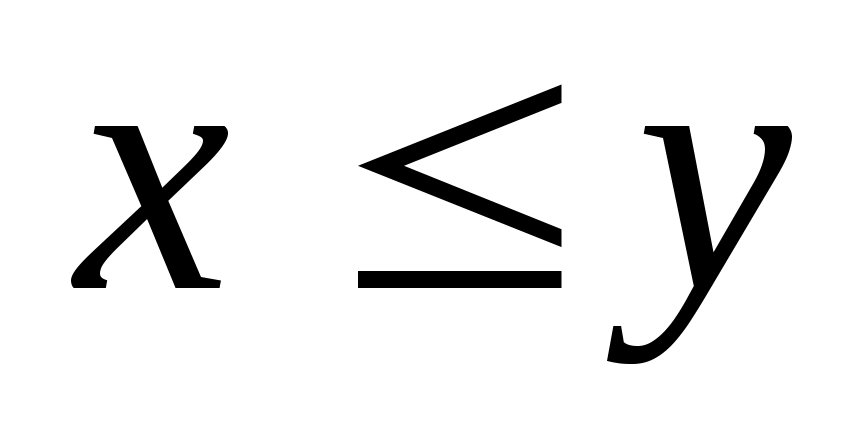 или или 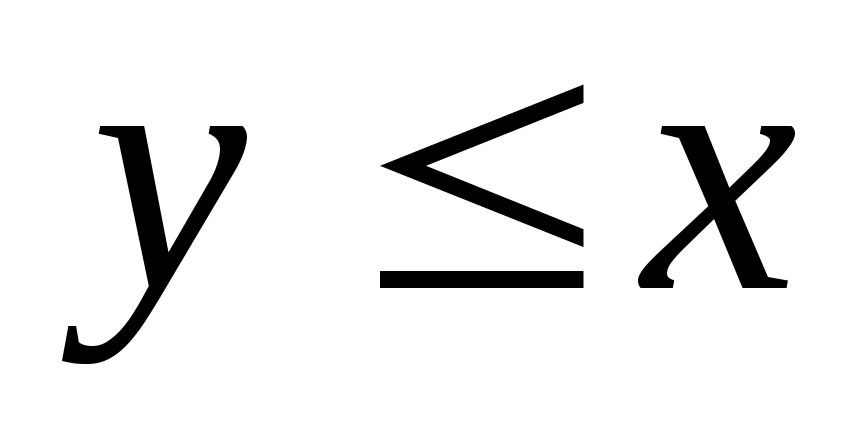 . .
Непустое множество  , на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством. Элемент , на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством. Элемент  частично упорядоченного множества частично упорядоченного множества  называется максимальным (минимальным), если для называется максимальным (минимальным), если для 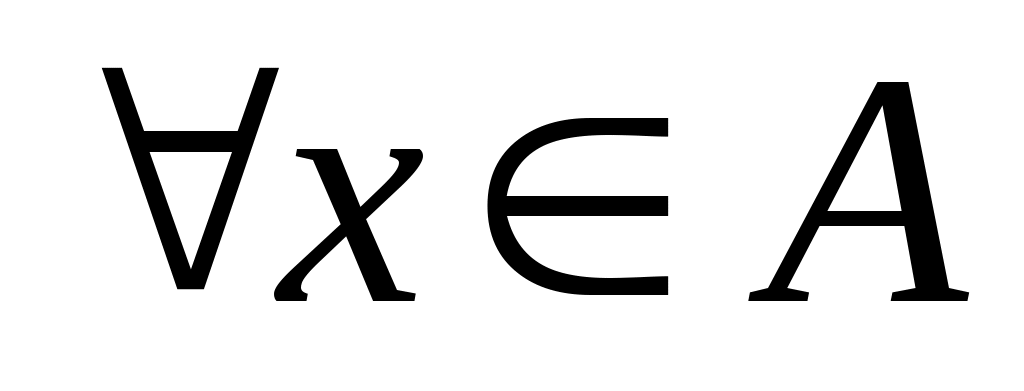 из того, что из того, что 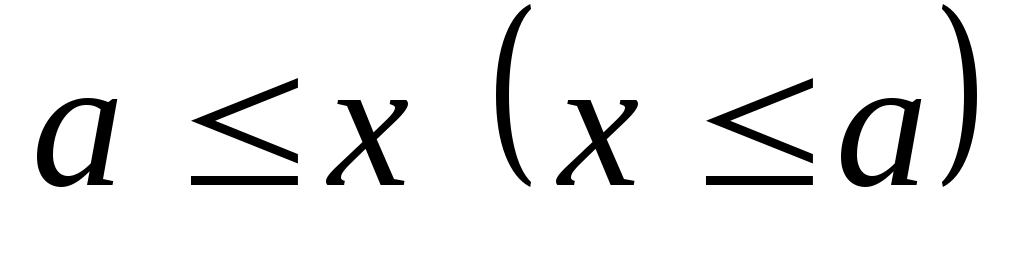 , следует , следует 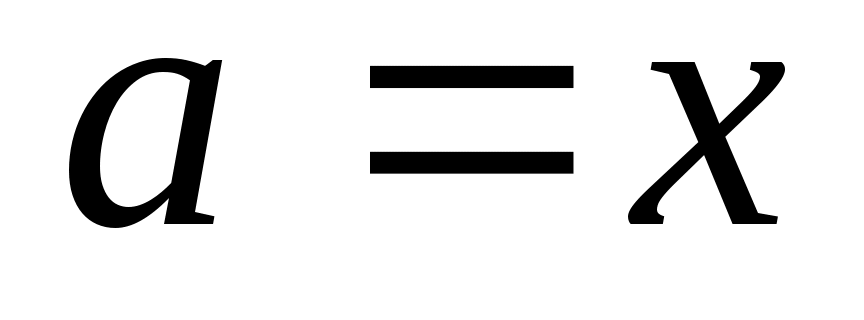 . Элемент . Элемент  называется наибольшим (наименьшим), если называется наибольшим (наименьшим), если 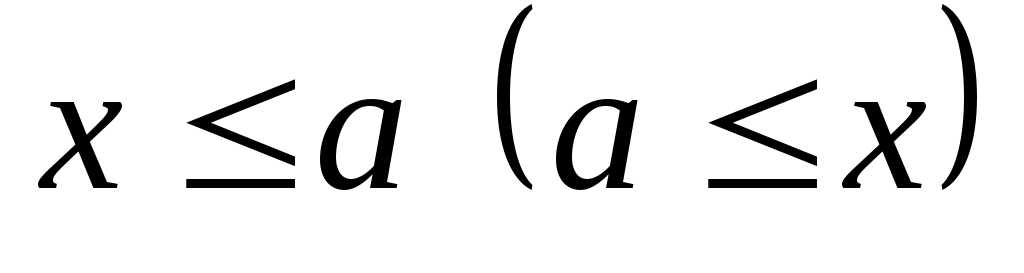 для всех для всех 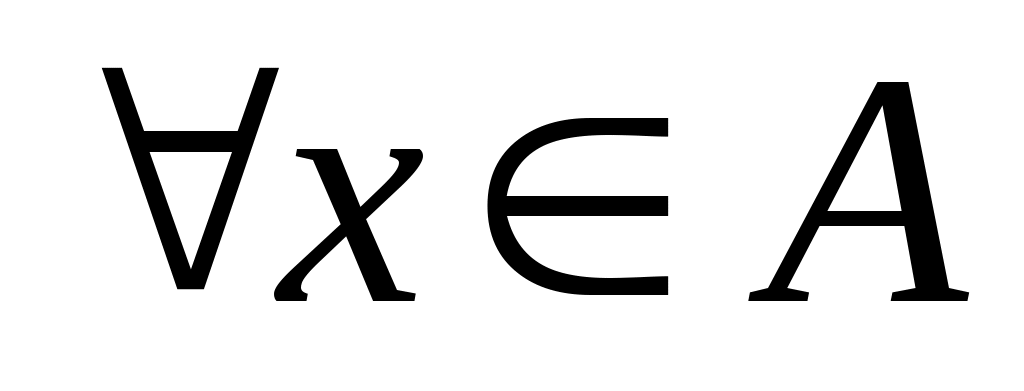 . Наибольший элемент обозначается . Наибольший элемент обозначается 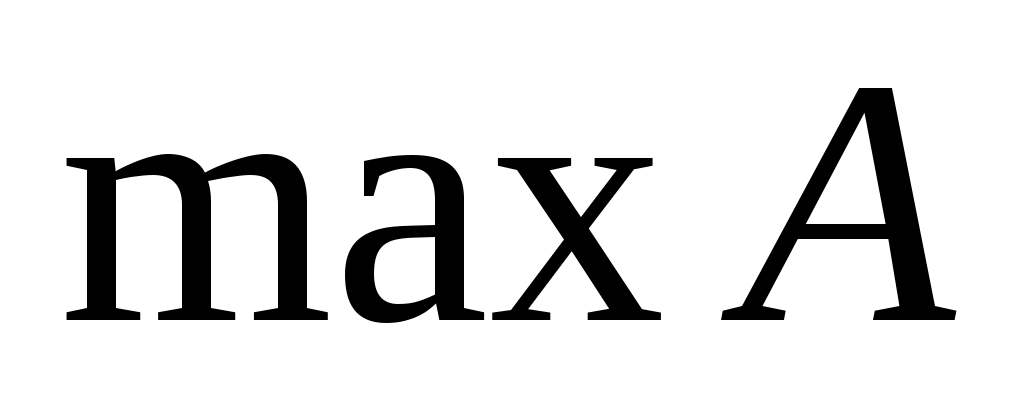 , наименьший — , наименьший — 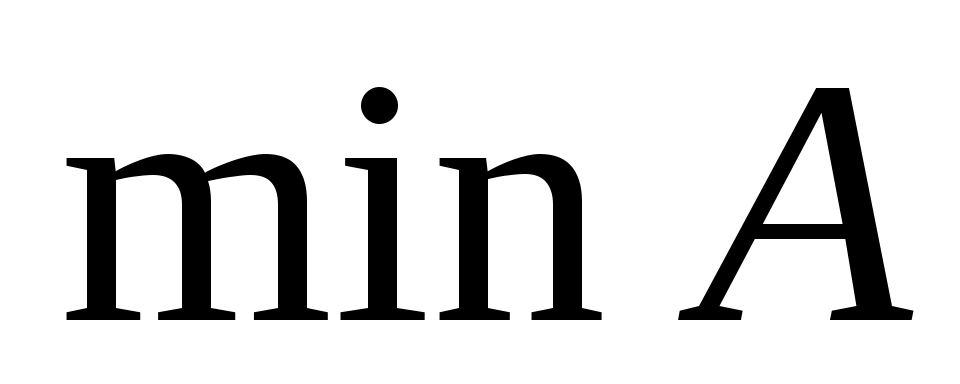 . Этих элементов у множества может и не быть, например, линейно упорядоченное множество рациональных чисел . Этих элементов у множества может и не быть, например, линейно упорядоченное множество рациональных чисел 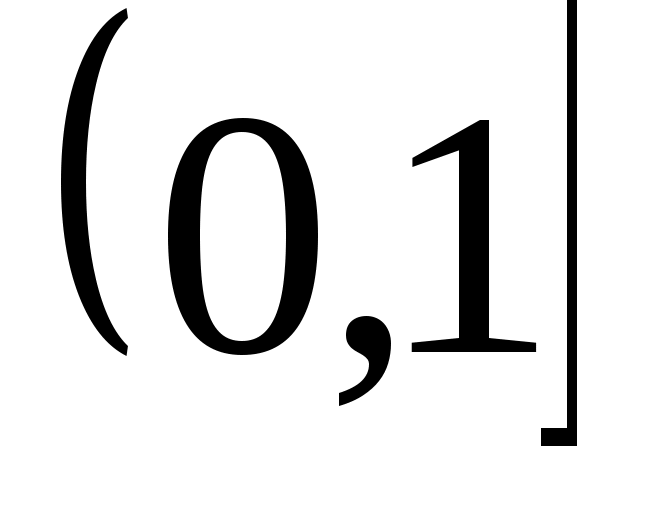 не имеет наименьшего элемента, наибольший элемент равен единице. не имеет наименьшего элемента, наибольший элемент равен единице.
Верхней (нижней) гранью подмножества 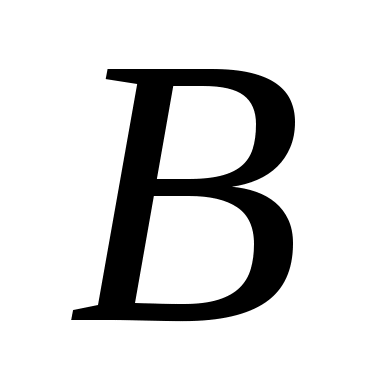 частично упорядоченного множества частично упорядоченного множества  называется всякий элемент называется всякий элемент  и такой, что и такой, что 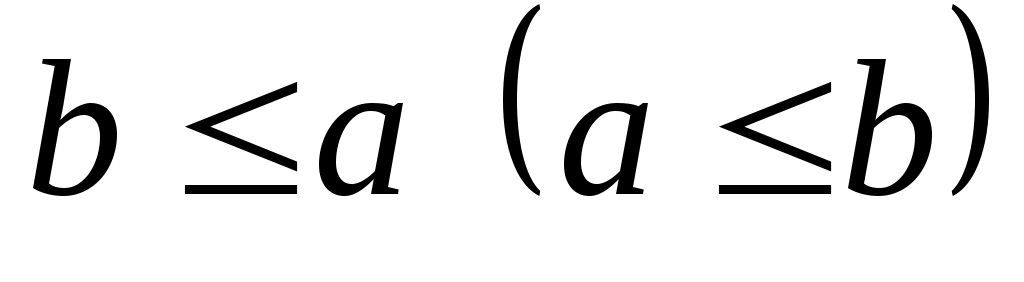 для всех для всех 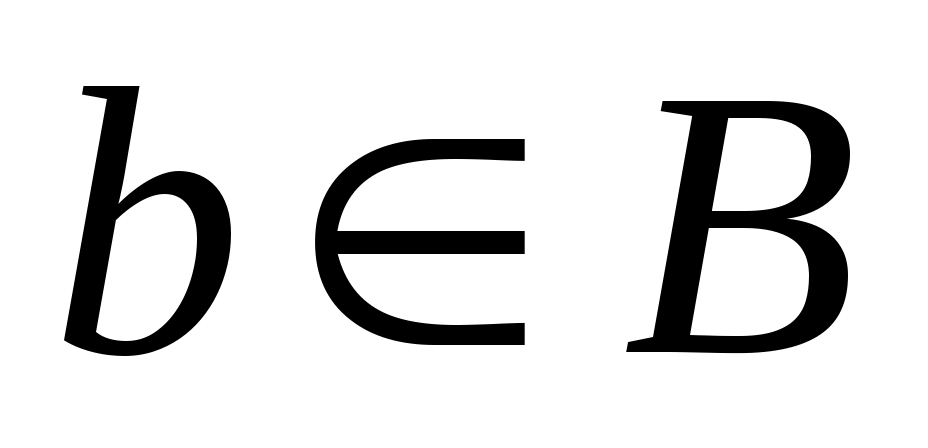 . Точной верхней (нижней) гранью подмножества . Точной верхней (нижней) гранью подмножества 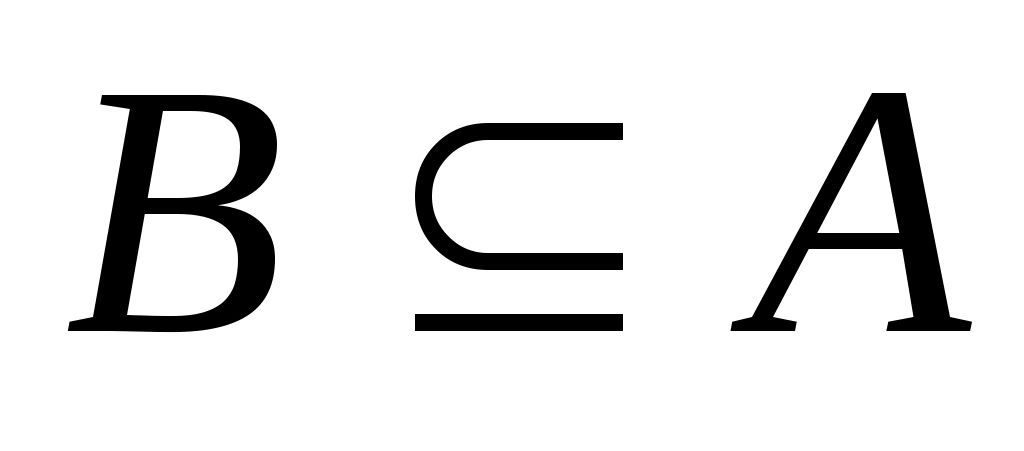 называется наименьшая верхняя (наибольшая нижняя) грань для называется наименьшая верхняя (наибольшая нижняя) грань для 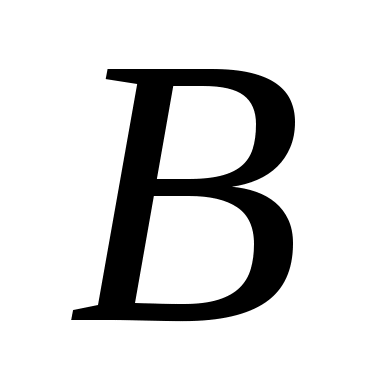 . Точная верхняя и точная нижняя грани множества . Точная верхняя и точная нижняя грани множества 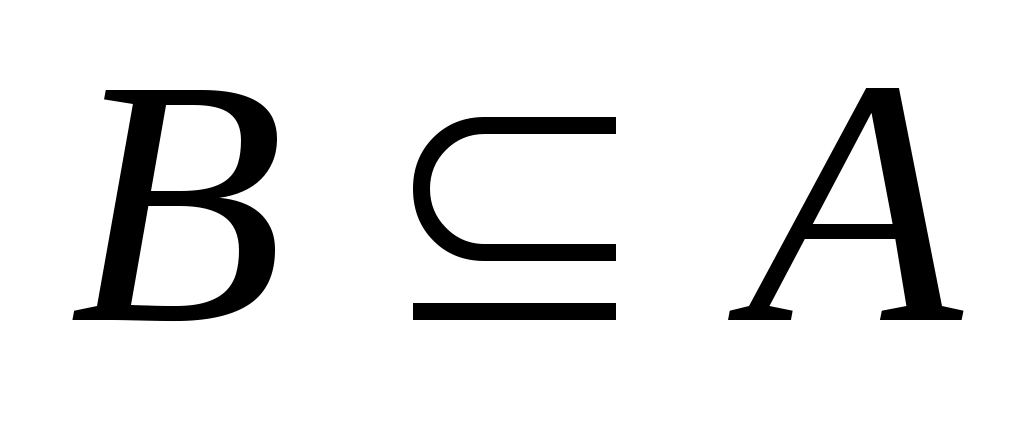 обозначаются через обозначаются через 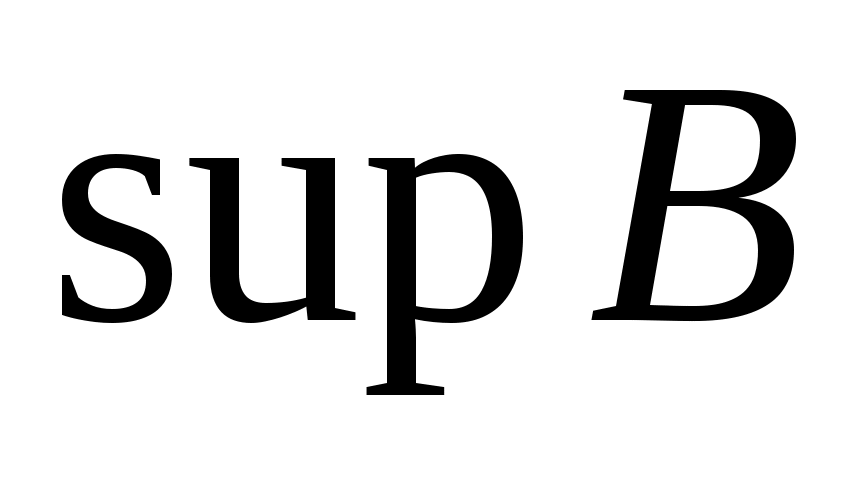 (супремум) и (супремум) и 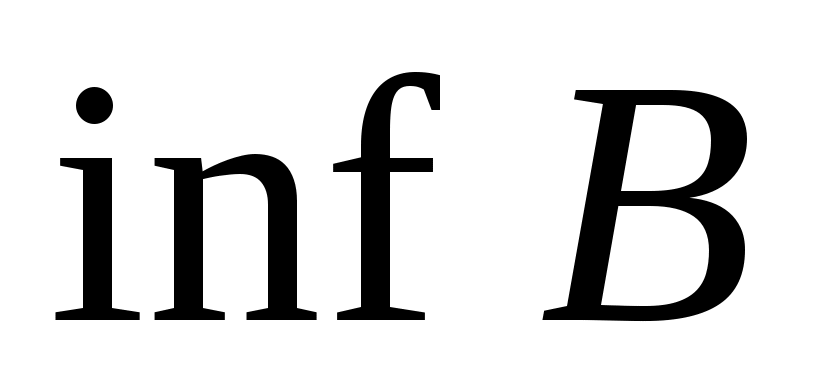 (инфимум) соответственно. (инфимум) соответственно.
Линейный порядок 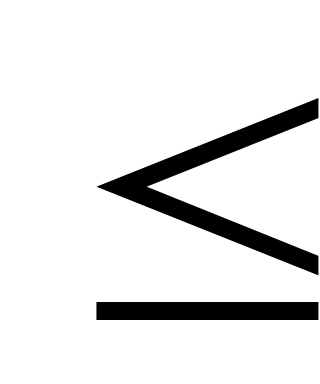 на множестве на множестве  называется полным, если каждое непустое подмножество множества называется полным, если каждое непустое подмножество множества  имеет наименьший элемент. В этом случае множество имеет наименьший элемент. В этом случае множество  называется вполне упорядоченным. называется вполне упорядоченным.
|
|
|
 Скачать 5.84 Mb.
Скачать 5.84 Mb.

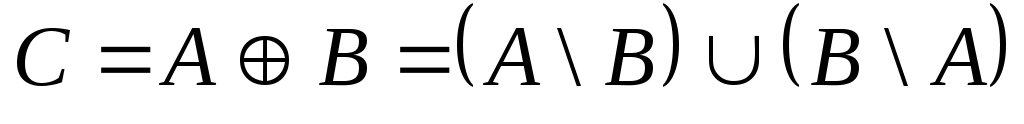 (рис. 1.11). Очевидно, что
(рис. 1.11). Очевидно, что 
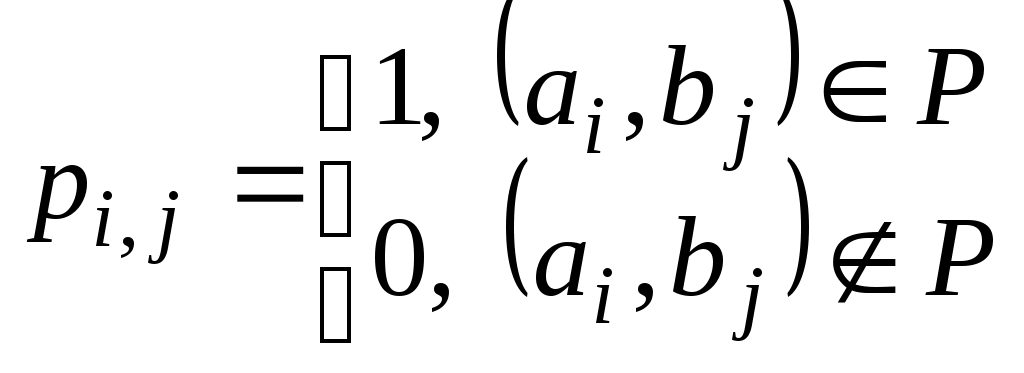 .
.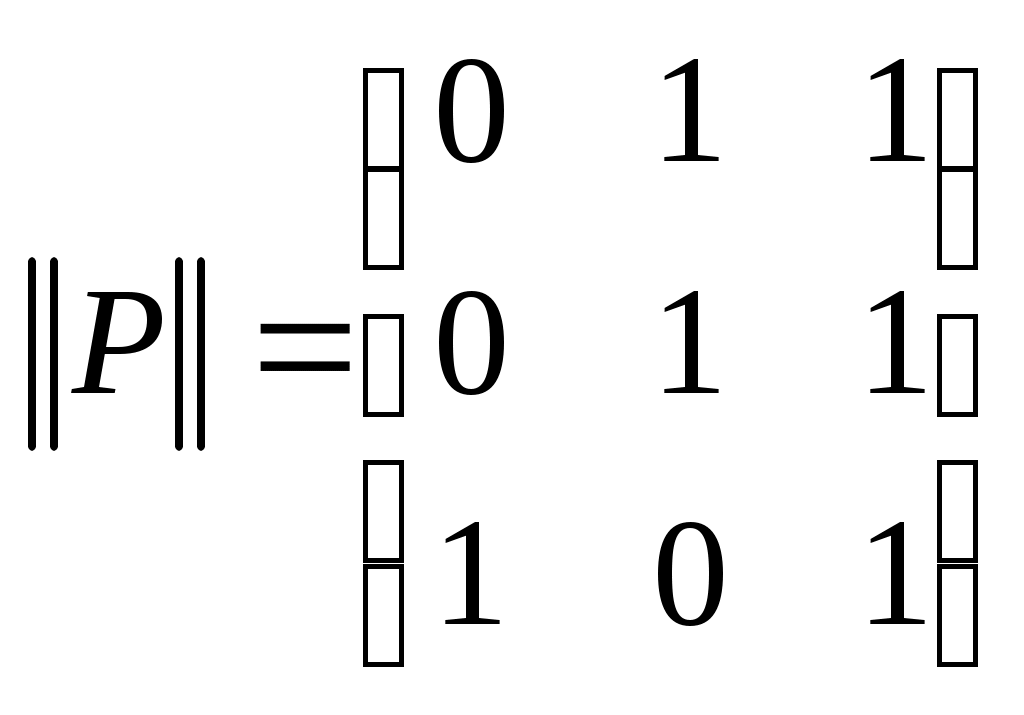 .
. 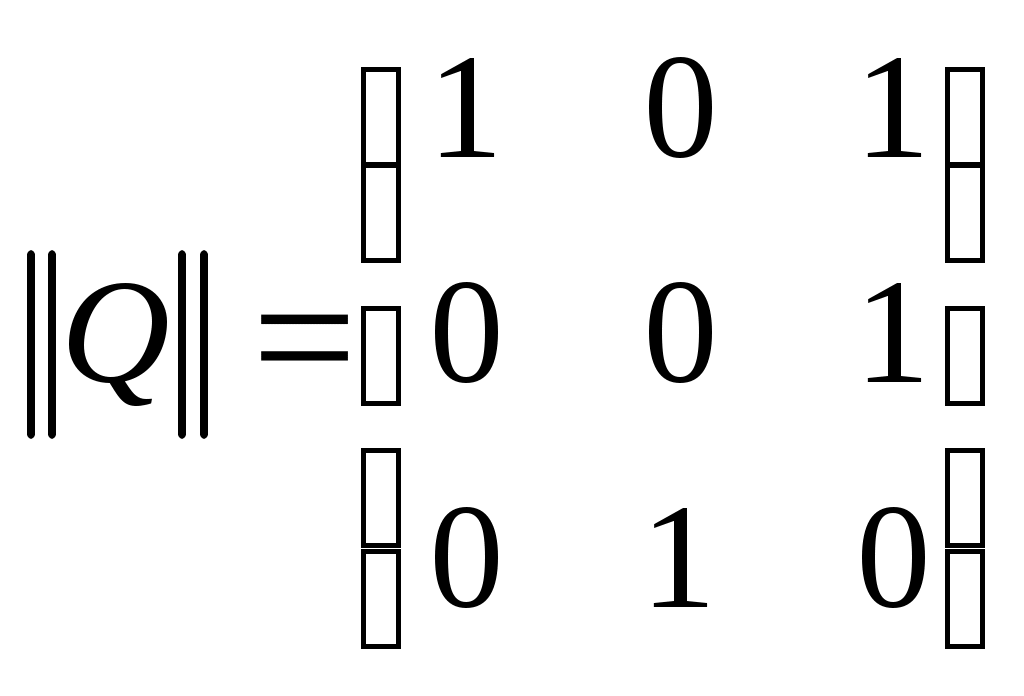 ,
,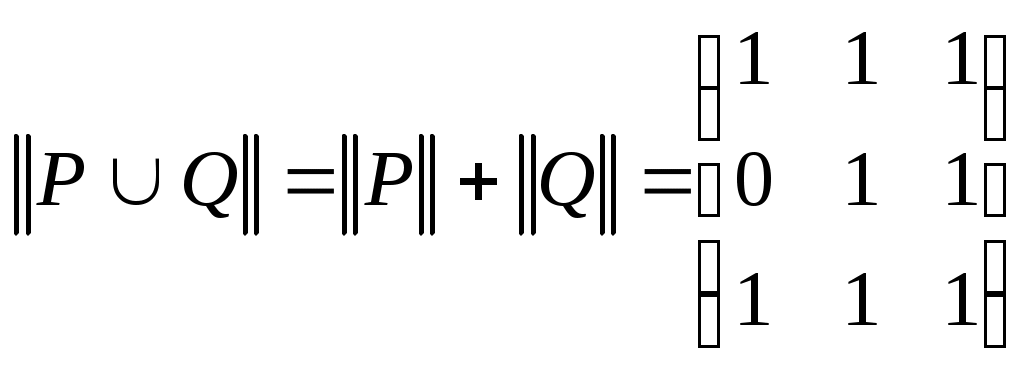 ,
, 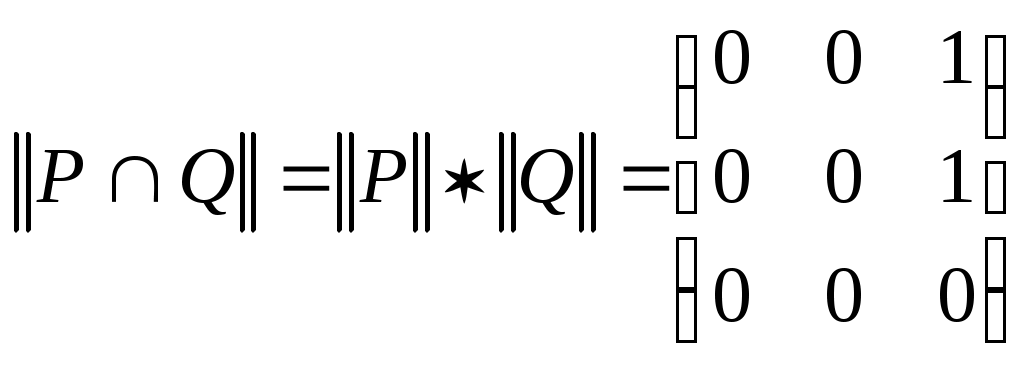 .
.
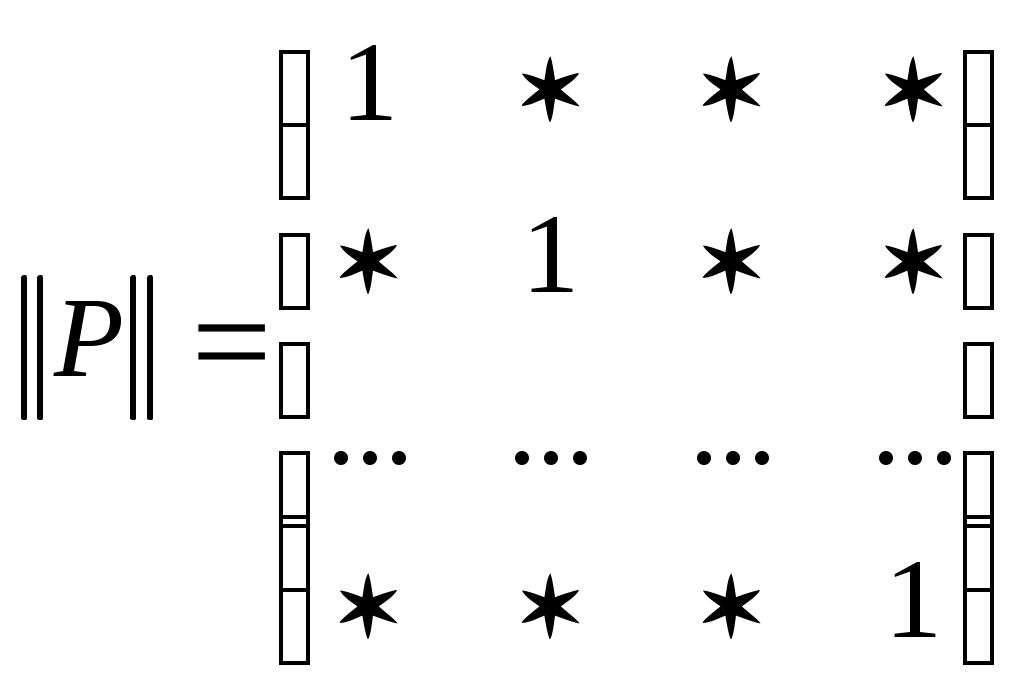 ,
,