Главная страница
Навигация по странице:

  • 7) Уравнение прямой

  • 8) Уравнение плоскости

  • 4

  • 11) Уравнение высоты пирамиды через вершину A

  • 11) Уравнение плоскости через вершину

    		•

    1-Задача-1,6. 1 Координаты векторов


    Скачать 36.52 Kb.
    Название1 Координаты векторов
    Дата06.01.2023
    Размер36.52 Kb.
    Формат файлаdocx
    Имя файла1-Задача-1,6.docx
    ТипДокументы
    #874082

    Даны координаты пирамиды: A1(1,-1,6), A2(4,5,-2), A3(-1,3,0), A4(6,1,5)
    1) Координаты векторов.
    Координаты векторов находим по формуле:
    X = xj - xi; Y = yj - yi; Z = zj - zi
    здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
    Например, для вектора A1A2
    X = x2 - x1; Y = y2 - y1; Z = z2 - z1
    X = 4-1; Y = 5-(-1); Z = -2-6
    A1A2(3;6;-8)
    A1A3(-2;4;-6)
    A1A4(5;2;-1)
    A2A3(-5;-2;2)
    A2A4(2;-4;7)
    A3A4(7;-2;5)
    7) Уравнение прямой
    Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:

    Параметрическое уравнение прямой:
    x=x0+lt
    y=y0+mt
    z=z0+nt
    Уравнение прямой A1A2(3,6,-8)

    Параметрическое уравнение прямой:
    x=1+3t
    y=-1+6t
    z=6-8t
    Уравнение прямой A3A4(7,-2,5)

    Параметрическое уравнение прямой:
    x=-1+7t
    y=3-2t
    z=0+5t
    8) Уравнение плоскости.
    Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

    x-x1
    y-y1
    z-z1

    x2-x1
    y2-y1
    z2-z1

    x3-x1
    y3-y1
    z3-z1










    = 0


    Уравнение плоскости A1A2A3

    x-1
    y+1
    z-6

    3
    6
    -8

    -2
    4
    -6










    = 0


    (x-1)(6·(-6)-4·(-8)) - (y+1)(3·(-6)-(-2)·(-8)) + (z-6)(3·4-(-2)·6) = -4x + 34y + 24z-106 = 0
    Упростим выражение: -2x + 17y + 12z-53 = 0
    Уравнение плоскости A1A2A4

    x-1
    y+1
    z-6

    3
    6
    -8

    5
    2
    -1










    = 0


    (x-1)(6·(-1)-2·(-8)) - (y+1)(3·(-1)-5·(-8)) + (z-6)(3·2-5·6) = 10x - 37y - 24z + 97 = 0
    10) Длина высоты пирамиды, проведенной из вершины A4(6,1,5).
    Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины: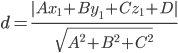

    Уравнение плоскости A1A2A3: -2x + 17y + 12z-53 = 0

    11) Уравнение высоты пирамиды через вершину A4(6,1,5).
    Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
    Уравнение плоскости A1A2A3: -2x + 17y + 12z-53 = 0


    11) Уравнение плоскости через вершину A4(6,1,5).
    Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
    A(x-x0) + B(y-y0) + C(z-z0) = 0
    Уравнение плоскости A1A2A3: -2x + 17y + 12z-53 = 0
    -2(x-6)+17(y-1)+12(z-5) = 0
    или
    -2x+17y+12z-65 = 0
    13) Угол между плоскостью A1A2A3 и плоскостью A1A2A4.
    Косинус угла между плоскостью A1x + B1y + C1 + D = 0 и плоскостью A2x + B2y + C2 + D = 0 равен углу между их нормальными векторами N1(A1, B1, C1) и N2(A2, B2, C2):

    Уравнение плоскости A1A2A3: -2x + 17y + 12z-53 = 0
    Уравнение плоскости A1A2A4: 10x - 37y - 24z + 97 = 0

    γ = arccos(-0.99117928326363) = 172.389o

    написать администратору сайта