задачи экзамен. 1. Мальчик на роликах пересёк прямоугольную площадку по диагонали ab, а второй мальчик прошёл пешком из точки a в точку
 Скачать 1.32 Mb.
|
|
1.Мальчик на роликах пересёк прямоугольную площадку по диагонали AB, а второй мальчик прошёл пешком из точки A в точку B по краю площадки. Определите модули перемещений обоих мальчиков и пути, пройденные ими, если размеры площадки 60 х 80 м.  2.На рисунке представлен график зависимости координаты туриста от времени. Опишите его движение. 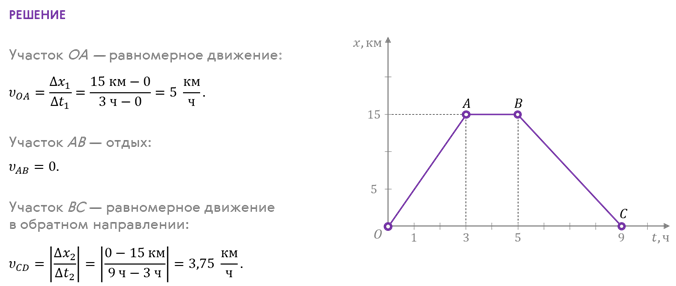 3.Две лодки плывут навстречу друг другу равномерно и прямолинейно. Скорость первой лодки 8 м/с, второй — 5 м/с. Определите время и координату их места встречи, если в начальный момент времени расстояние между лодками равно 130 м  4. на рисунке представлен график зависимости скорости точки от времени. Определите, в какой момент времени координата точки станет равной 30 м, если в момент начала наблюдения её координата равнялась –6 м. Определите скорость точки в этот момент времени.  5. Космическая ракета при старте с поверхности Земли движется вертикально с ускорением 20 м/с2. Найти вес лётчика-космонавта массой 80 кг в кабине при старте ракеты.  6. Тело массой 50 кг тянут по горизонтальному участку пути, прикладывая силу под углом 60о к горизонту. Модуль прикладываемой силы равен 200 Н), а модуль силы трения скольжения — 100 Н. Определите модуль ускорения тела.  7. При помощи динамометра ученик перемещал деревянный брусок массой 200 г по горизонтально расположенной доске. Каков коэффициент трения, если динамометр показывал 0,6 Н?  8.Тело некоторой массы поднимают вертикально вверх из состояния покоя, прикладывая силу 70 Н. За первые 2 с равноускоренного движения тело поднимается на высоту 8 м. Определите массу тела. Сопротивление воздуха не учитывайте. .  9.На соревнованиях лошадей тяжелоупряжных пород, одна из них перевезла груз массой 23 т. Найдите коэффициент трения, если сила тяги лошади 2,3 кН .  .10.Движение материальной точки описывается уравнением x=5-8t+4t^2.приняв ее массу,равной 2 кг,найти импульс через 2 и 4 секунды после начала отсчета времени  11.Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия, если удар неупругий?  12. Башенный кран поднимает в горизонтальном положении стальную балку длиной 5 м и сечением 100 см2 на высоту 12 м. Какую полезную работу совершает кран?  13. Тело брошено вверх с начальной скоростью 20 м/с. Если за нулевой уровень потенциальной энергии принять поверхность Земли, то на какой высоте кинетическая энергия тела будет равна его потенциальной энергии? Сопротивлением воздуха можно пренебречь, а ускорение свободного падения принять равным 10 м/с2. При решении данной задачи систему тело — Земля будем считать изолированной.  Ответ: 5. 14.Пуля массой 50 г вылетает из ствола ружья вертикально вверх со скоростью 40 м/с. Чему равна потенциальная энергия пули через 4 с после начала движения? Сопротивлением воздуха пренебречь. Решение. Пуля под действием одной постоянной силы тяжести совершает равноускоренное движение, поэтому для вычисления высоты подъёма достаточно воспользоваться формулой  Подставив h в формулу потенциальной энергии, получим:  . Ответ: 40 Дж.15. Какую мощность развивает альпинист массой 80 кг, поднявшийся на высоту 500 м за 2 ч?  16. При температуре 320 К средняя квадратичная скорость молекулы кислорода 500 м/с. Определить массу молекулы кислорода. T=320 К, υкв=500 м/с, m0–?Решение задачи:Как и в механике, среднюю кинетическую энергию молекул кислорода можно определить по формуле: Eк=m0υ2кв2С другой стороны, есть формула связи средней кинетической энергии с абсолютной температурой: Eк=32kT. Приравняем правые части этих двух формул: m0υ2кв2=32kT Выразим из этого равенства массу одной молекулы m0: m0=3kTυ2квНапомним, что здесь k – это постоянная Больцмана, равная 1,38·10-23 Дж/К. Посчитаем ответ: m0=3⋅1,38⋅10–23⋅3205002=5,3⋅10–26кг=5,3⋅10–23 Ответ: 5,3·10-23 г. 17.Чему равна температура газа, если при концентрации 2,65·1025 м-3 он создает давление 98,8 кПа?Решение задачи: Воспользуемся формулой связи давления p с концентрацией молекул n и абсолютной температурой газа T: p=nkTВ этой формуле k – это постоянная Больцмана, равная 1,38·10-23 Дж/К. Из этой формулы выразим искомую температуру T: T=pnk Посчитаем численный ответ задачи: T=98,8⋅1032,65⋅1025⋅1,38⋅10–23=270,2К≈–3∘C 18.В комнате размером 4x5x2,7 м3 испарился кристаллик йода массой 20 мг. Сколько молекул йода оказалось в 1 см3 воздуха комнаты при условии их равномерного распределения? Молярная масса йода равна 127 г/моль. Дано:a=4 м, b=5 м, c=2,7 м, m=20 мг, V0=1 см3, M0=127 г/моль, N0−? Решение задачи: В случае равномерного распределения молекул йода по объему комнаты число его молекул N0 в объеме V0 можно определить через концентрацию n по формуле: N0=n⋅V0(1) Концентрация молекул n равна отношению количества всех молекул йода N к объему комнаты V: n=NV Объем комнаты V легко найти как объем прямоугольного параллелепипеда: V=abc Число всех молекул N найдем как произведение количества вещества ν на число Авогадро NА: N=νNАКоличество вещества ν равно отношению массу всего йода m к молярной массе йода M. Учитывая, что молярная масса M молекулярного йода I2 в два раза больше молярной массы M0 атомарного йода I, указанной в условии, имеем: ν=m2M В итоге, если подставить все приведенные формулы в формулу (1), получим: N0=mNАV02MabcЧисло Авогадро равно 6,022·1023 моль-1. Переведем некоторые величины в систему СИ:20мг=20⋅10–6кг 1см3=10–6м3 127г/моль=0,127кг/мольПосчитаем численный ответ:N0=20⋅10–6⋅6,022⋅1023⋅10–62⋅0,127⋅4⋅5⋅2,7=8,8⋅1011 19.Каково давление азота, если его плотность равна 1,35 кг/м3, а средняя квадратичная скорость молекул 500 м/с? Дано: ρ=1,35 кг/м3, υкв=500 м/с, p−? Решение задачи: Запишем для начала уравнение Клапейрона-Менделеева: pV=mMRTПоделим обе части уравнения на объем V, в правой части получившееся отношение mV заменим на плотность газа ρ: p=mMVRTp=ρMRT(1) Среднюю квадратичную скорость молекул υкв определяют по такой формуле: υкв=3RTM−−−−−√ Выразим из выражения температуру газа T: T=Mυ2кв3R Это выражение подставим в формулу (1), тогда получим: p=ρMRMυ2кв3R p=13ρυ2кв Задача решена в общем виде. Все величины, входящие в формулу, даны в единицах системы СИ, поэтому можно сразу посчитать ответ: p=13⋅1,35⋅5002=112500Па=0,1 Задание 20 Удельная теплоёмкость стали равна 500 Дж/кг·°С. Что это означает? 1) при охлаждении 1 кг стали на 1 °С выделяется энергия 500 Дж 2) при охлаждении 500 кг стали на 1 °С выделяется энергия 1 Дж 3) при охлаждении 1 кг стали на 500 °С выделяется энергия 1 Дж 4) при охлаждении 500 кг стали на 1 °С выделяется энергия 500 Дж Решение. Удельная теплоемкость характеризует количество энергии, которое необходимо сообщить одному килограмму вещества для того, чтобы нагреть его на один градус Цельсия. Таким образом, для нагревания 1 кг стали на 1 °С необходимо затратить энергию 500 Дж. Задания 21 На графике представлены результаты измерения количества теплоты Q, затраченного на нагревание 1 кг некоторого вещества, при различных значениях температуры t этого вещества. Погрешность измерения количества теплоты ΔQ = ±500 Дж, температуры Δt = ±2 °C.  Выбери два утверждения, соответствующие результатам этих измерений. 1) Удельная теплоёмкость вещества примерно равна 600 Дж/(кг·°C) 2) Для нагревания до 90 °C необходимо сообщить больше 50 кДж. 3) При охлаждении 1 кг вещества на 20 °C выделится 12000 Дж. 4) Для нагревания 2 кг вещества на 30 °C необходимо сообщить примерно 80 кДж. 5) Удельная теплоёмкость зависит от температуры. Решение. Проверим справедливость предложенных утверждений 1) Теплоту, переданную телу можно вычислить по формуле: Поэтому зависимость  — прямая. Проведём аппроксимационнуюпрямую на графике: Откуда удельная теплоёмкость 2) Для нагревания до 90 °C необходимо сообщить телу меньше 50 кДж энергии. 3) При охлаждении 1 кг вещества на 20 °C выделится 4) Для нагревания 2 кг вещества на 30 °C необходимо сообщить примерно 5) Удельная теплоёмкость не зависит от температуры Таким образом, верными являются утверждения под номерами 1 и 3. Ответ: 13. Задание 22  На рисунке представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания? Ответ дайте в кДж. (Удельная теплоёмкость свинца — )Решение. Из графика находим, что за 10 минут свинец нагрелся на 227 – 27 = 200 °C. Вычислим количество теплоты, полученное свинцом: Ответ: 26. Задача № 23 Действуя силой 80 Н, человек поднимает из колодца глубиной 10 м ведро воды за 20 с. Какую мощность развивает при этом человек?  Задача № 24. Определите КПД двигателя автомобиля, которому для выполнения работы 110,4 МДж потребовалось 8 кг бензина. Задача № 25 Определите КПД двигателя автомобиля, которому для выполнения работы 220,8 МДж потребовалось 16 кг бензина. 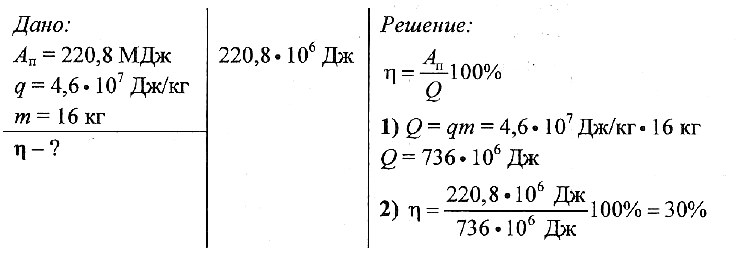 Задача № 26 Патрон травматического пистолета «Оса» 18 x 45 мм, содержит резиновую пулю массой 8,4 г. Определите КПД патрона, если пуля при выстреле приобрела скорость 140 м/с. Масса порохового заряда патрона составляет 0,18 г, удельная теплота сгорания пороха 3,8 • 106 Дж/кг.  Задача № 27 ЕГЭ Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найти КПД цикла ɳ.  Задача № 28 Двигатель внутреннего сгорания мощностью 36 кВт за 1 ч работы израсходовал 14 кг бензина. Определите КПД двигателя.  Задача № 29. В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?  Задача № 30 Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.  |